基于响应面模型与遗传算法的无轭分块电枢轴向磁场永磁电机齿槽转矩优化

徐龙江，牟 磊，汤 磊，刘 烨，彭 寅

(国网山东省电力公司青岛供电公司，山东 青岛 266002)

0 引 言

轴向磁场永磁电机与径向磁场永磁电机相比具有高径长比、高转矩密度及高运行效率的特点，在电牵引驱动，特别是在电动汽车的轮毂或轮边驱动中具有优越性。相对于普通的轴向磁场永磁电机，无轭分块电枢轴向磁场永磁电机(YASA)没有电枢轭部，因电机定子铁心磁路短、定子铁心用量少而更具有优越性。YASA电机定子分块铁心若采用软磁复合材料(SMC)模压而成，不但可以简化铁心的制造难度，而且能够充分利用SMC材料磁、热及机械的各向同性的特点，进一步提高电机的性能。作为一种高性能永磁电机，YASA电机首先提出并应用于电动汽车的轮毂驱动[1]，而后得到了很好的开发和运用[2]。

齿槽转矩是所有永磁电机必须面对的问题，文献[3]采用3-D FEM的方法，对基于叠压硅钢材料的普通轴向磁场永磁电机降低齿槽转矩的诸多方法进行研究和综述，包括永磁体极弧系数、转子永磁体斜极、定子双边槽口偏移对齿槽转矩的影响。文献[4]和文献[5]都采用3-D FEM方法对基于叠压硅钢材料的YASA电机的齿槽转矩进行了分析，特别在文献[5]中，提出了采用转子磁体径向分块轴向偏移的方法降低齿槽转矩。显然，文献[3-5]给出的方法可以用于降低基于叠压硅钢材料的YASA电机的齿槽转矩，但是，由于基于SMC的YASA电机具有特殊的磁路结构及导磁材料，其齿槽转矩的分析方法与结论也会有所不同，为进一步降低该电机的齿槽转矩，必须采用多种方法分析并进行优化设计。

本文针对基于SMC的YASA电机进行齿槽转矩的分析与优化设计。第1部分介绍了电机的结构特征，在给出电机初始设计参数的基础上，将该电机与基于叠压硅钢材料的YASA电机各自产生的齿槽转矩进行对比。第2部分研究了基于SMC的YASA电机齿槽转矩的削弱方法，首先分析了永磁体极弧系数对齿槽转矩及电机性能的影响，然后在选定理想极弧系数的前提下，分别研究了永磁体斜极、定子齿靴宽度系数和定子齿靴偏移对齿槽转矩的削弱作用。第3部分通过响应面模型和遗传算法对电机的齿槽转矩进行优化设计研究。第4部分利用3-D FEM对电机齿槽转矩的优化设计结果进行了验证。

1 YASA电机齿槽转矩及初始设计参数

1.1 YASA电机的结构

电机的齿槽转矩源于定子齿槽存在而产生的气隙磁导谐波与转子永磁体磁动势谐波之间的相互作用[3]，实际上，齿槽转矩是由永磁体产生的气隙磁通与变化的气隙磁阻相互作用而产生，具体表现为一系列谐波转矩的合成[6]

(1)

式中，θm为定转子的相对位置角，Tk和φk分别为齿槽转矩第k次谐波的幅值和相位，Nc为永磁体极数2p与定子槽数Zs的最小公倍数。

从另一个角度看，齿槽转矩是由磁铁边缘与定子槽之间的相互作用产生的，它的出现是由于磁链与定子开槽引起的定子磁阻变化之间的相互作用

(2)

式中，φgap为永磁体的气隙磁通，R为定子磁阻。

从式(2)可以看出，改变φgap或R均会对电机的齿槽转矩产生影响，其中优化永磁体极弧系数和磁体斜极角度可以降低φgap的大小，优化定子槽口宽度和槽口偏移角度可以降低dR/dθ的大小，因此本文通过分析这4个因素的影响来优化电机的齿槽转矩。

针对轴向磁场永磁电机，3-D FEM是分析齿槽转矩的最理想方法[3-5]。如前文所述，有很多方法可以用于轴向磁场永磁电机齿槽转矩的降低，如调整永磁体极弧系数及定子槽口宽度等，这些方法在其他电机中都得到很好的分析和应用，但针对基于SMC的YASA电机，由于结构及导磁材料的不同，必将表现出不同的特点。为采用3-D FEM方法对基于SMC的YASA电机的齿槽转矩进行分析与计算，下面先对所研究的电机进行描述。

图1为3相10极12槽YASA电机的结构示意图。可以看出，转子盘采用实心导磁材料和10极表贴式永磁体设计，两转子盘对应的永磁体结构为N-S型。中间定子的12个分块铁心采用SMC材料模压而成，为充分利用SMC的各向同性磁特性，在半径方向上，各铁心块齿靴部分突出齿身部分(如图2所示)，从而使线圈端部位于电机的有效磁场范围内。值得注意的是，该电机采用分数槽绕组，可以削弱齿槽转矩中除γk(γ=Nc/Zs)次以外的谐波，降低齿槽转矩[7-8]。

图1 YASA电机结构示意图

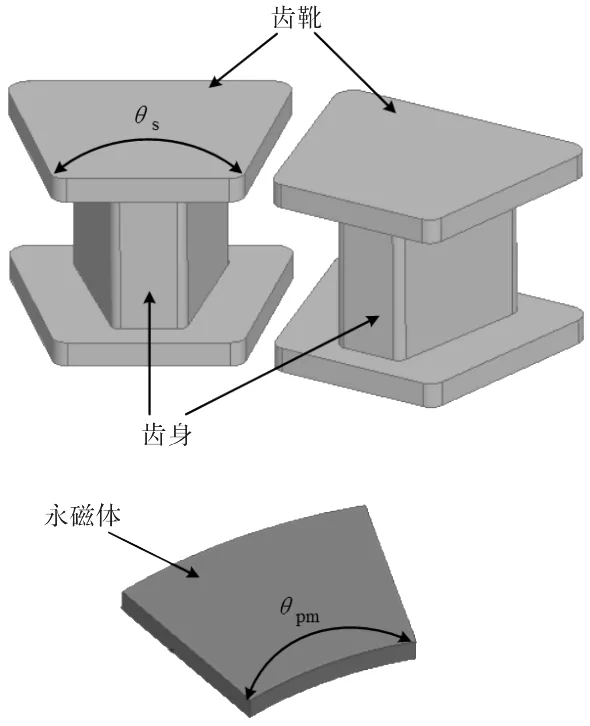
图2 YASA电机的定子铁心模块及永磁体结构

表1为计算电机齿槽转矩的初始设计参数，其中转子永磁体采用扇形结构，定子齿靴采用梯形结构(如图2所示)。永磁体极弧系数αpm可以用极弧角度θpm与极距的比值来表示：αpm=2p×θpm/360；定子齿靴宽度系数αs可以用齿靴角度θs与齿距的比值来表示：αs=Zs×θs/360。

表1 YASA-AFPM电机主要设计参数

图3为上述电机的齿槽转矩波形及将该电机定子铁心改为叠压硅钢材料时的波形比较，从图中可以看出，基于SMC的YASA电机的齿槽转矩虽然小于基于叠压硅钢材料的YASA电机，但数值依然较高，因此需进一步研究降低其齿槽转矩的方法，具体内容在第2部分详细阐述。

图3 基于SMC和叠压硅钢材料的YASA电机齿槽转矩

2 齿槽转矩降低方法研究

2.1 永磁体极弧系数

图4为通过3-D FEM计算得出的不同永磁体极弧系数下的齿槽转矩波形及峰值变化，从图中可以看出：

图4 极弧系数对齿槽转矩的影响

(1)该电机的齿槽转矩波形具有较好的正弦对称性，随极弧系数的变化，齿槽转矩波形的幅值所在位置基本不变。显然这一不同齿槽转矩波形及齿槽转矩随极弧系数的变化，源于该电机采用分数槽绕组，削弱了齿槽转矩中的特定谐波成分，波形呈良好的正弦性。

(2)永磁体极弧系数不但影响电机的齿槽转矩，更影响气隙磁通，从而影响电磁转矩的大小。显而易见的是，极弧系数对电动势波形的正弦性具有重要影响，非正弦的空载反电动势波形会在正弦波驱动永磁电机中产生纹波转矩。经分析，该电机在极弧系数为0.72时不但具有较小的齿槽转矩，且具有足够的气隙磁密用以产生电磁转矩，该极弧系数下的空载反电动势波形也相对较好，因此本电机的极弧系数定为0.72，在此基础上，分析其他参数变化对齿槽转矩的影响。

2.2 永磁体斜极

YASA电机的永磁体贴于转子盘表面，几何外形简单，相对于径向电机，永磁体斜极更容易实现。轴向磁场永磁电机的斜极有多种方法，如三角形斜极、梯形斜极等[9]。为操作方便，本文采用扇形永磁体斜极方法，如图5所示，扇形永磁体外弧不变，内弧偏移β角度。

图5 永磁体斜极示意图

图6为永磁体斜极角度变化对齿槽转矩的影响，可以看出，基于SMC的YASA电机转子永磁体斜极对齿槽转矩的影响具有不同于一般轴向磁场永磁电机和基于叠压硅钢材料的YASA电机的特点。随斜极角度的增大，齿槽转矩开始降低较为明显，但在斜极角度大于3°后，再增加斜极角度，齿槽转矩降低较小，在斜极角度达到6°左右时，再增加斜极角度，齿槽转矩逐渐增加，而且显然，较高的斜极角度会降低电机的平均磁通量。

图6 永磁体斜极角度对齿槽转矩的影响

2.3 齿靴宽度系数

如前文所述，YASA电机定子分块铁心的齿靴为梯形结构，由于SMC材料导磁率很低，且由于SMC的机械问题，定子齿靴厚度设计较大，达到5mm，因此定子齿靴宽度系数对齿槽转矩和齿靴间漏磁具有不同于叠压硅钢电机的特点。

图7和图8分别为齿靴宽度系数αs变化对齿槽转矩和空载反电动势有效值的影响，其中图8中空载反电动势波形的变化即是定子齿靴间漏磁的变化。由图7可以看出，定子齿靴宽度系数αs增大时，齿槽转矩先降低，然后再增大，在αs增大到0.866时，再增加αs对齿槽转矩影响较小；由图8可以看出，随αs增大，空载反电动势趋于降低，但降低较少。综合上述分析，本电机的定子齿靴宽度系数为0.8左右时具有低的齿槽转矩和高的空载反电动势。

图7 定子齿靴宽度系数对齿槽转矩的影响

图8 定子齿靴宽度系数对空载反电动势的影响

2.4 齿靴偏移

电机的总齿槽转矩由组成电机的各个齿槽产生的齿槽转矩叠加而成，对基于SMC的YASA电机来说，可以很容易实现各定子铁心两面齿靴的错位，使两面齿靴产生的齿槽转矩波形相位偏移，从而削弱总齿槽转矩。图9为电机每个定子铁心模块上下齿靴中心线之间的偏移，齿靴偏移角度δ用上下槽口中心线之间的夹角表示。

图9 定子齿靴偏移示意图

对不同齿靴偏移角度下的齿槽转矩进行计算，得到的齿槽转矩波形如图10(a)所示，图10(b)给出了齿槽转矩幅值随齿靴偏移角度的变化关系，可以看出，随齿靴偏移角度δ的增大，齿槽转矩首先减小，然后再增大，针对本电机的分析，当δ=1.5左右时具有较小的齿槽转矩。

图10 定子齿靴偏移角度对齿槽转矩的影响

3 基于响应面模型和遗传算法的电机齿槽转矩优化

由前述分析可以看出，在固定电机永磁体极弧系数αpm，从而保证电机的基本永磁磁通量和电磁转矩后，转子永磁体斜极角度β、定子齿靴宽度系数αs和定子齿靴偏移角度δ都会对齿槽转矩造成影响，通过选择合适的β、αs、δ就可以使电机具有最小的齿槽转矩。下面通过建立响应面模型，并采用遗传算法对YASA电机的齿槽转矩进行优化设计。

3.1 响应面模型建立

响应面法(RSM)是通过一系列确定性试验，对某个响应受多个变量影响的问题进行建模和分析[10]。通过建立响应面模型，对各变量进行优化，可以得到最佳响应值。

本文选择永磁体斜极角度β、定子齿靴宽度系数αs和定子齿靴偏移角度δ为设计变量，齿槽转矩Tcog为响应函数，在各变量取值范围内选取合适的样本点，并通过三维有限元获取各样本点下对应的响应值，最后根据试验结果建立设计变量与响应变量之间的响应面模型。

由前述3-D FEM分析可知，当固定极弧系数定为0.72时，β、αs、δ的取值范围分别取[5，9]、[0.733，0.866]、[1，3]，电机的峰值齿槽转矩值较小，因此选定上述变量范围建立响应面模型，根据各设计变量的取值范围选取13组样本点数据，通过3-D FEM计算得到的齿槽转矩响应值如表2所示。

表2 各样本点计算结果

响应变量与设计变量之间的关系可以用二次多项式表示为

(3)

式中，m为变量个数，n为求解次数，xi为设计变量，Tcog为响应函数，ε为随机误差向量。

由多元函数求极值的必要条件，可得

(4)

用矩阵表示为

(5)

根据表2的计算结果，最终建立Tcog与β、αs、δ之间的数学模型为

(6)

3.2 基于遗传算法的齿槽转矩优化

本文将响应面模型与遗传算法相结合，利用响应面模型来计算个体适应度值，通过遗传算法得到最大适应度个体，具体流程如图11所示。

图11 遗传算法优化流程

在齿槽转矩优化过程中保持电机的输出功率恒定，反电动势在一定合理的范围内，然后选取响应面的3个设计参数为优化变量，以实现齿槽转矩最小为优化目标，对电机进行优化，其具体问题可以归结为

(7)

式中，Un代表电机的额定相电压有效值，PN代表电机的额定功率。

图12为目标函数的优化过程，可以看出，经过约20代的优化搜索，目标函数Tcog趋于收敛，其中各变量的具体变化过程如图13所示。

图12 目标函数Tcog的变化

图13 各优化变量随迭代过程的变化

表3给出了YASA电机齿槽转矩优化结果，可以看出，当β、αs、δ分别为7.2°、0.783、2.2°时，齿槽转矩从原先的2.14Nm降低为0.18Nm，优化效果显著。

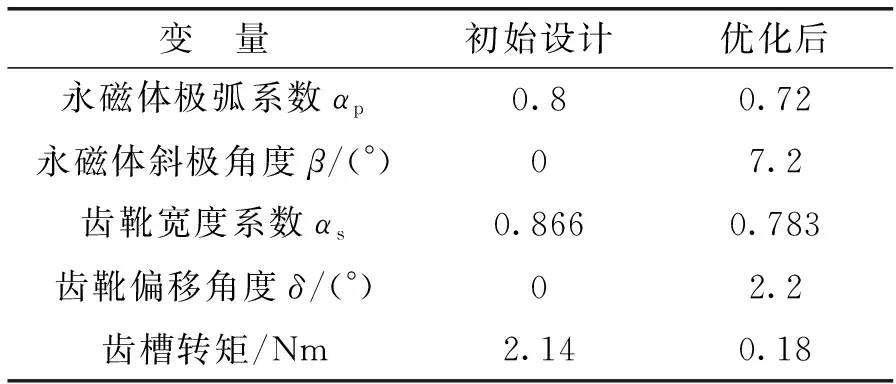
表3 齿槽转矩优化结果

4 有限元验证

为了验证上述优化过程的准确性，采用3-D FEM分别对电机初始设计及优化后的齿槽转矩进行计算，结果如图14所示。可以看出，优化后的齿槽转矩峰值计算结果为0.195Nm(与优化结果0.18Nm相比，误差为7.6%)，相比于初始设计方案的齿槽转矩降低了约91%。

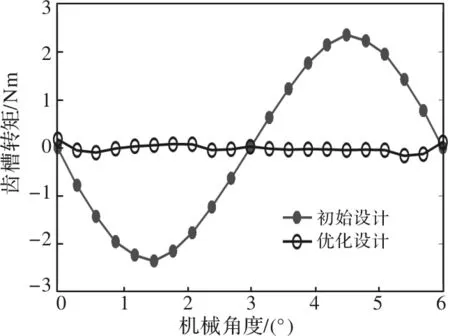
图14 齿槽转矩波形对比图

图15为n=1200r/min时优化前后的空载反电动势波形及额定负载转矩波形，可以看出，优化前后空载反电动势及电磁转矩大小基本不变，而优化后的空载反电动势波形更加平滑，谐波畸变率仅为1.7%，额定负载时的转矩脉动也由优化前的8.9%降低为3.5%。

图15 优化前后空载反电动势和电磁转矩波形

5 结 论

本文针对基于SMC的YASA电机的齿槽转矩进行分析及优化设计，得到以下结论：

(1)由于SMC具有比叠压硅钢材料低的相对导磁率，基于SMC的YASA电机也具有比基于叠压硅钢材料的YASA电机更低的齿槽转矩。

(2)永磁体极弧系数、转子永磁体斜极、定子齿靴宽度系数和定子齿靴偏移均会对电机的齿槽转矩产生影响，针对基于SMC的YASA电机，其齿槽转矩随各因素的变化有着与普通轴向磁场永磁电机和基于叠压硅钢材料的YASA电机不一样的特点。

(3)在确定合理的永磁体极弧系数αpm的前提下，选取转子永磁体斜极角度β、定子齿靴宽度系数αs和定子齿靴偏移角度δ为优化参数，通过建立响应面模型并利用遗传算法对基于SMC的YASA电机的齿槽转矩进行优化设计，使电机的齿槽转矩由优化前的2.14Nm降低为0.18Nm，而电机额定运行时的转矩脉动峰峰值只占额定转矩的3.5%，且优化前后电机的空载反电动势及电磁转矩大小基本保持不变。