非对称延迟对正余弦编码器的影响及补偿策略
杨 敏,杨盼龙, 王 新,虞国平,金 泱
(1.浙江省火力发电高效节能与污染物控制技术研究重点实验室,杭州 311121;2.浙江浙能技术研究院有限公司,杭州 311121; 3.华中科技大学,武汉 430000; 4.浙江浙能电力股份有限公司,杭州 310007)
0 引 言
随着大功率发电机组的持续稳定运行及其带来的稳定经济效益,针对各种类型的故障诊断技术也随之诞生,文献[1-3]对这些故障诊断技术进行了介绍。伴随着嵌入式技术的发展及运动控制理论的不断深入,一种新型的发电机组不抽转子膛内故障检测技术随之诞生。该技术取代了传统过度依赖人工的检测模式,将智能测试平台挂载在转子护环上进行制定齿槽的特种作业。由于发电机定转子齿槽连续且间距相等,想通过平台自动控制精准定位就需要配合高精度的编码器位置采集方案,加之发电机组内环境因素复杂,所以平台上用来计步的编码器必须具有足够强的抗干扰性能且尺寸要尽可能小。按照工作原理可以将编码器主要分为光电式和磁电式两种。光电编码器可以通过光电传感器将待测的机械位置转化为脉冲或数字量进行输出。磁电编码器通过磁电传感器将待测的机械转动转化为电信号的变化,之后通过对电信号解码将机械位置转换成数字信号进行输出。由于磁电编码器需要对模拟信号进行解码,因此在精度方面比光电编码器差,但磁电编码器具有抗干扰性强,低功耗,体积小等优点,因而在发电机组内部的检测平台中更为适用。
磁电编码器通过对磁传感器输出的正余弦信号值进行采样并进一步细分得到待测平台的实时位置信息。目前主流的细分算法主要有CORDIC算法,查表法,闭环反馈跟踪法等。文献[4-8]主要介绍了通过坐标旋转来进行反正切细分得到角度的CORDIC算法,该算法所占内存较小,在保证迭代次数的条件下精度也可以得到保证。文献[9-12]对闭环反馈跟踪算法进行了研究,这种算法通过在采样值与输出角度之间建立闭环系统来调节输出角度。现有研究也对由于安装或器件偏差造成的直流误差、幅值误差、相位误差等方面的影响以及补偿方法进行了研究。文献[13-15]通过Matlab仿真的方法,分别对三种偏差对角度细分以及转速测量等方面的影响进行了分析。文献[16]提出了采用卡尔曼滤波对正余弦信号进行过滤以减小误差的方法。文献[17-18]提出了模拟量补偿以及数字量补偿等偏差补偿方法。
这些研究中,均假设正余弦信号的采样延时均等,均等延时不会影响到细分的精度。由于实际工况以及硬件条件的限制,正余弦两路信号延时可能会出现不等的情况,此时可能会出现正弦信号超前于余弦信号,或者余弦信号超前于正弦信号的情况。在这种情况下编码器的精度就会大大下降,进而影响到发电机智能故障检测设备的精准位置信息采集和计步。
针对实际使用过程中编码器正余弦信号采样延时不均等所带来的计步偏差,本文在对传统编码器位置信息采集处理进行探究的基础上对复杂工况下的延时正余弦信号延时不均等的问题进行了深入分析,并进一步提出了新的采样策略来解决由于延时不等所造成的偏差。仿真和实验结果证明所提出的方案可以有效提高编码器的采样精度,且增强了发电机故障智能检测平台的计步精确性与抗干扰性。
1 传统细分算法
AMR3003L是一款基于AMR效应的角度传感器芯片,可以测量 0~180°范围内的磁场角度,其输出电压正比于两倍磁场角度的正弦或余弦。AMR3003L内部包含两个独特的推挽式惠斯通电桥,每个惠斯通电桥包含四个高灵敏度AMR传感元件,输出信号的峰值可达工作电压的1.6%。此外,独特的 AMR惠斯通电桥结构有效地补偿了传感器的温度漂移。AMR3003L采用标准的LGA封装,具有封装体积小,装配方便的特点。AMR3003芯片内部集成了8个AMR效应磁电阻,通过特殊的内部结构设计, 当磁场某一个时刻角度为θ时,V(x)=Acos(2θ),V(y)=Asin(2θ),其中A、B为常数,利用反正切函数,即可得到磁场的角度信息。
根据以上介绍的AMR3003L的工作原理可以得到实现磁编码器的方法。首先在AMR3003L的表面上放置一块小磁铁,该磁铁在旋转过程中可以在该芯片处产生磁场,磁场的角度与磁场旋转的角度一致,且磁场的方向平行于芯片表面。在旋转的磁场下,该传感器的典型输出曲线如图1所示。
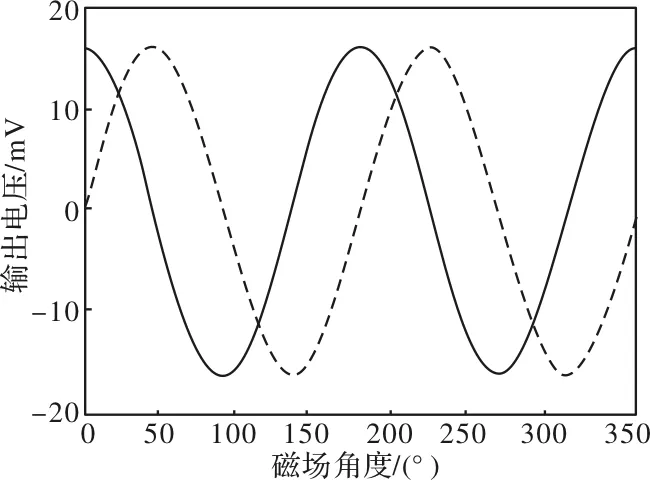
图1 AMR3003L传输特性曲线
根据以上输出特性曲线可以看出,可以通过旋转磁场产生周期性的正余弦信号。通过对正余弦信号进行解码就可以得到实时角度。
CORDIC算法的基本原理在于坐标旋转。假设坐标系上有一点坐标为(x,y),那么可以通过坐标旋转将该点以原点为中心旋转到x轴上,在这个过程中旋转走过的角度就是该点对应的角度。如果以原点为中心将该点顺时针旋转θ,那么旋转后的坐标为

(1)
可以借助二分查找的方法,先将该点以原点为中心顺时针旋转45°,如果旋转后的纵坐标小于0,那么就将该点再逆时针旋转22.5°,否则继续顺时针旋转22.5°。可以重复这一过程多次直到纵坐标足够接近0。把该过程中所有顺时针旋转过的角度求和并减去逆时针旋转过的角度,最后得到的角度就是该点坐标的初始角度。可以通过处理来尽可能减少乘法次数并进一步将乘法转换成移位操作。首先减少乘法次数:

(2)
为了进一步简化计算,可以把式(2)中的cosθ略掉,这样一来每次旋转后的新坐标点到原点的距离都变长了,放缩的系数是1/cosθ,但是对坐标点所对应的角度并无影响。这样的变形非常的简单,但是每次循环的运算量一下就从4次乘法降到了2次乘法。此外,还可以将tanθ取1/2,1/4等值,这样一来可以通过移位操作实现乘法来进一步加快运算速度。
2 传统的误差分析及补偿机制
在理想情况下,传感器输出的正弦信号与余弦信号应该完全正交,幅值相同,直流偏置为
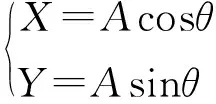
(3)
然而在实际情况下,由于机械安装的偏差以及器件本身的误差,传感器输出的正余弦信号将会产生偏差,主要的偏差有直流偏差,幅值偏差,相位偏差。这样一来正弦信号与余弦信号将变成:
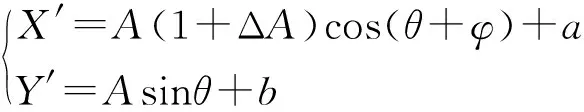
(4)
式中 ,ΔA代表余弦信号相对于正弦信号的幅值偏差,A为正弦信号的幅值,φ为余弦信号相对于正弦信号的相位偏差,a为余弦信号的直流偏差,b为正弦信号的直流偏差。这样当采用查表法或者CORDIC算法等方法进行解码时,在角度为θ时,利用实际采样到的正余弦值X′和Y′计算得到的角度为
(5)
此时计算得到的角度与实际角度的误差为θ′-θ。为消除这个角度误差,可以考虑采用校准查表法。通过另一个高精度的编码器与磁电编码器同轴旋转,记录下每个时刻计算得到的磁电编码器的θ′以及与之对应的高精度编码器的角度η,则η可以看成是θ′所对应的实际角度θ。通过这个方法可以建立一个足够精度的标准表,表中存储磁电编码器角度所对应的实际角度。这样在每次计算磁电编码器的角度θ′时,可以通过把这个角度θ′索引号,去找到标准表中与之对应的实际角度。通过这个方法可以找到每个所对应的实际角度,消除偏差所造成的角度计算误差。
校准查表法可以有效补偿正余弦信号的直流偏差误差,幅值偏差和相位偏差,从而提高细分精度。但是,在传统方案中,均假设正弦和余弦信号上的电路和采样延时均等,并认为均等延时不会对精度造成影响。然而,由于工况和硬件条件的限制,正弦和余弦两路的信号延时可能会出现不等的情况。这种延时偏差会造成细分误差。
3 非对称线路延时影响及补偿方案
在实际应用中很多因素会造成正弦和余弦信号采样延时不对称,无论是只采用一路ADC通道来对正弦信号以及余弦信号进行交替采样,还是采用两路ADC通道来分别对正弦信号以及余弦信号进行采样,两者采样之间都会存在一定的时间差。两者间的时间差将会导致计算角度时所使用的正弦信号与余弦信号存在相位差。本章节将针对此问题进行分析。
3.1 对称延时影响
当正弦与余弦信号延时相等时,正弦与余弦信号表达为
(6)
此时
(7)
可以看出,对称延时不会对转速的精度造成影响,只会造成角度结果的滞后。这种滞后只影响环路响应性能,但不影响细分精度。这也是众多研究不考虑采样延时影响的原因。
3.2 非对称采样延时影响
由于ARM内核的主芯片大多只有一个ADC转换缓存寄存器,导致不能同时进行两路ADC的采样。当对正弦以及余弦信号进行分别采样时,两者之间将会存在一定的延时误差,这个误差将进一步导致两者之间的相位存在一定偏差。根据采样情况,两者之间的相位超前情况主要包括正弦信号采样超前于余弦,余弦信号采样超前于正弦两种情况。下面分别对这两种情况产生的原因以及对角度细分的影响。
3.2.1 正弦信号采样超前于余弦信号
如果按照正弦-余弦循环交替采样的方式进行采样且在两次角度细分的时间间隔内可以进行偶数次采样,那么每次用来角度细分的正弦信号将超前于余弦信号,正弦信号以及余弦信号的数学表达式可分别表示为
(8)
式中,A为正余弦信号的幅值,ω为角速度,t0为两者之间的采样延时,此时解码求得的角度为
(9)
该角度与实际角度的偏差为
(10)
已知三角变换式
(11)
同时对式(10)两边取正切化简之后可以得到
(12)
在细分误差很小的情况下 ,则式(12)可以化为
(13)
通过Matlab仿真正弦信号超前于余弦信号时对角度计算以及转速的影响特性曲线如图2所示。
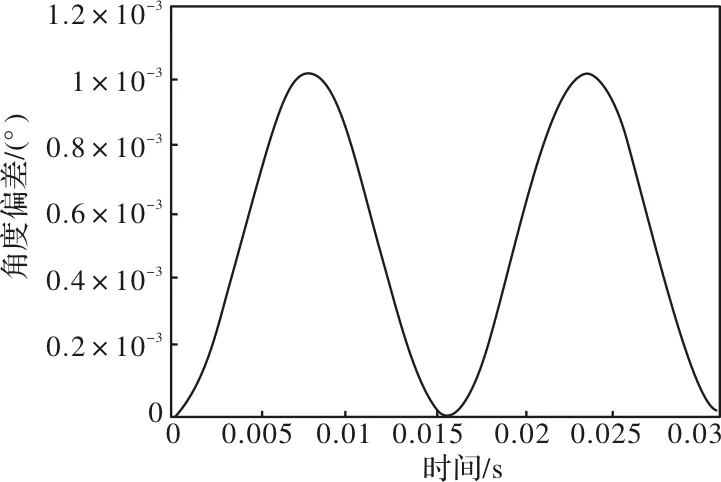
图2 给定转速为960r/min时角度偏差
由图2和图3可以看出,当正弦信号的采样超前于余弦信号的采样时,计算得到的角度与实际角度间会存在一定的偏差并且这个偏差值呈正余弦分布。与此同时,根据计算得到的角度可以求出电机转速,此时电机的转速与给定转速同样存在一定的偏差。由图4可以看出,转速偏差随着给定转速的增加而增加;由图5可以看出,转速偏差随着延时时间的增加而增加,并且转速偏差与延时时间大小呈线性关系。

图3 给定转速为960r/min时转速波动
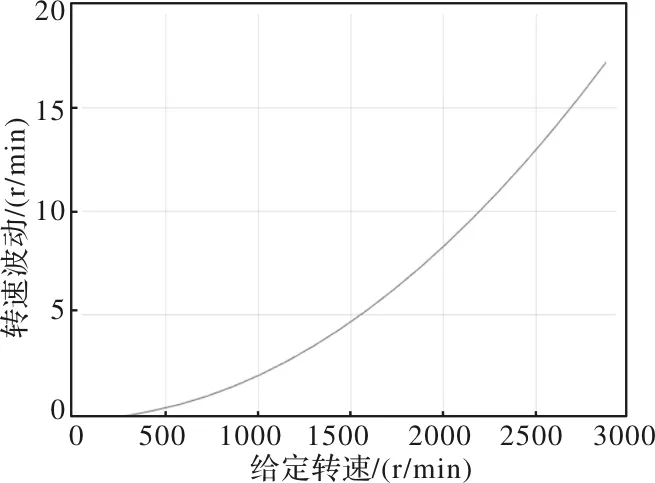
图4 转速波动随给定转速变化图

图5 转速波动随t0变化图
3.2.2 余弦信号采样超前于正弦信号
如果按照余弦-正弦循环交替采样的方式进行采样且在两次角度细分的时间间隔内可以进行偶数次采样,那么每次用来角度细分的余弦信号将超前于正弦信号,正弦信号以及余弦信号的数学表达式可分别表示为
(14)
此时解码求得的角度为
(15)
该角度与实际角度的偏差为
(16)
利用三角变换式(11)对式(16)两边取正切,化简后得到
(17)
在细分误差很小的情况下tanθ≈θ,则式(17)可改写为
(18)
通过Matlab仿真余弦信号超前于正弦信号时对角度计算以及转速的影响特性曲线如图6所示。

图6 给定转速为960r/min时角度偏差
由图6和图7可以看出,当余弦信号的采样超前于正弦信号的采样时,计算得到的角度与实际角度间会存在一定的偏差并且这个偏差值呈正余弦分布。与此同时,根据计算得到的角度可以求出电机转速,此时电机的转速与给定转速同样存在一定的偏差。由图8可以看出,转速偏差随着给定转速的增加而增加,并且差值原来越大;由图9可以看出,转速偏差随着延时时间的增加而增加,并且转速偏差与延时时间大小呈线性关系。
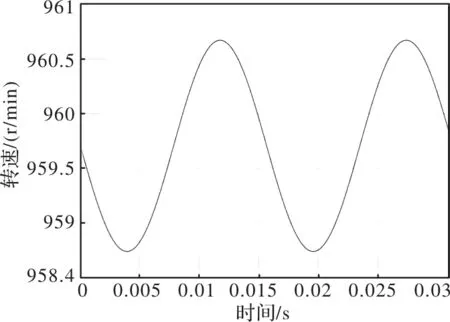
图7 给定转速为960r/min时转速波动

图8 转速波动随给定转速变化图

图9 转速波动随t0变化图
3.3 补偿方案
根据以上的分析可以看出,当正弦采样与余弦采样之间存在采样延时,通过计算得到的角度与实际角度将存在一定的偏差而且转速也将存在偏差。考虑到采样延时产生的原因,可以采取正弦-余弦-余弦-正弦的采样策略来尽可能减少采样延时造成的影响。假设采样时间间隔为t0,则四次采样的数据表达式为
sin1=Asin(ωt)
cos1=Acos(ωt+ωt0)
cos2=Acos(ωt+2ωt0)
sin2=Asin(ωt+3ωt0)
(19)
当t0很小的时候
(20)
(21)
此时正弦与余弦可近似看成为同一时刻的采样值。
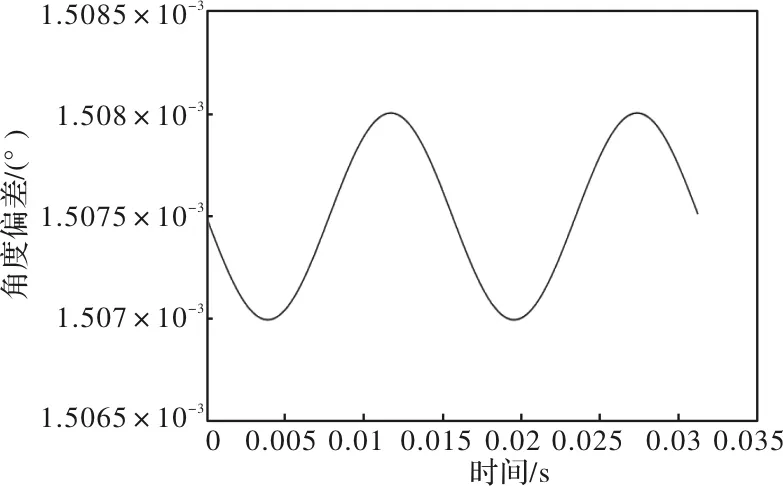
图10 给定转速为960r/min时角度偏差

图11 给定转速为960r/min时转速波动
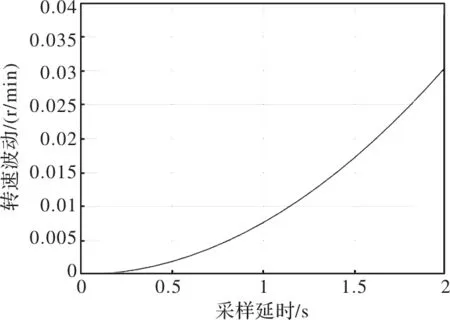
图12 转速波动随给定转速变化图
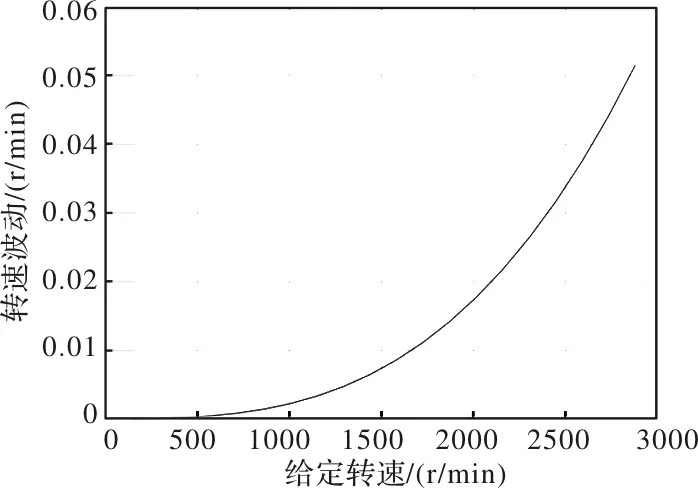
图13 转速波动随t0变化图
由上图可以看出,当采用新的采样策略后,在不同转速以及不同延时大小的情况下,转速的波动得到了有效的改善,精度得到了进一步的提升。在转速达到3000r/min,t0=0.00005s时转速波动仅为0.05r/min。相比之下,精度得到了明显的改善。
4 实 验
使用装有23位高精度编码器的伺服电机以1200r/min的速度转动,在另一侧使用磁电编码器测量转速,反馈角度计算频率为3kHz。正弦和余弦不同演示情况下的转速波动以及采样新的采样策略后转速波动如图14~图16所示。

图14 正弦采样超前余弦时转速波动
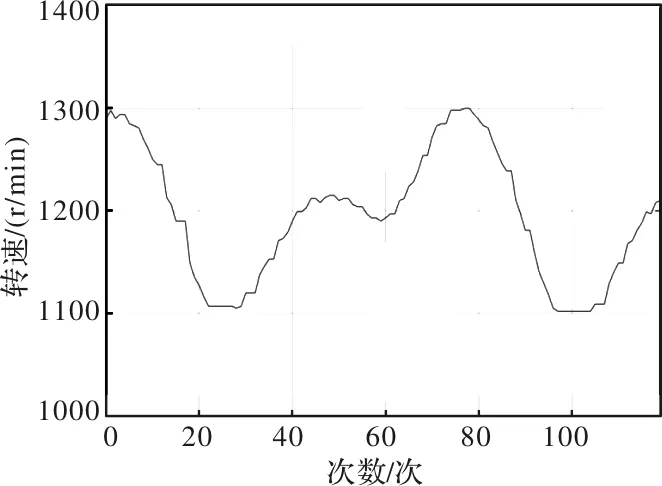
图15 余弦采样超前正弦时转速波动
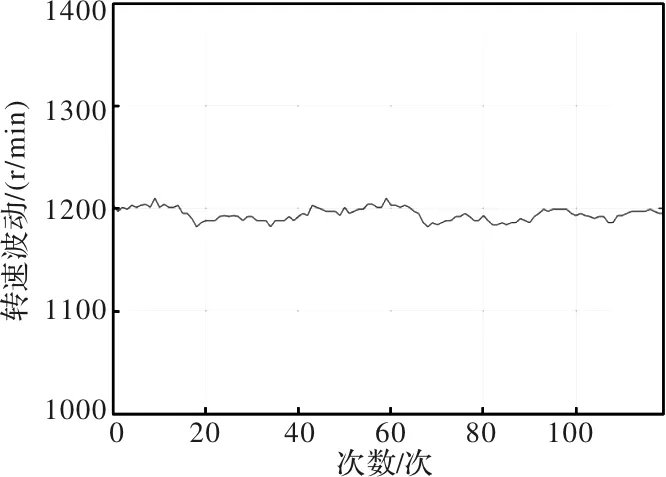
图16 采用新的采样策略后转速波动
由以上实验图形可以看出,在电机以1200r/min的给定转速转动时,当正弦采样超前于余弦或者余弦采样超前于正弦时,转速波动超过了±50r/min;在采用新的策略后,转速波动保持在±20r/min以内,精度有了明显的改善。
5 结 论
根据仿真结果以及实验结果可以看出,当发电机故障智能检测平台上使用的编码器的正弦信号以及余弦信号之间存在采样延时,采用常规的细分得到的角度将会和实际角度存在一定偏差而且位置信息的测量也将存在较大波动。采用本文提出的采样策略可以很大程度上减小采样采样延时的影响,尽可能提高编码器的精度,保证了智能检测平台位置信息采集的精度及计步的准确。
——编码器

