磁阻式旋转变压器极槽配合研究
杜 龙,徐志科,金 龙,姚更生,陈松涛
(1. 东南大学 电气工程学院,南京 210096; 2. 镇江赛尔尼柯自动化有限公司,江苏 镇江 212000)
0 引 言
为了掌握电机转子的位置信息,获得更好的控制性能,通常需要转子位置传感器。常见的位置传感器有光电编码器和旋转变压器。但是光电编码器不适合在高温和振动环境中使用,机械安装也很困难[1-2]。而旋转变压器能够产生高精度位置信号,结构简单且稳定可靠,可以很方便的集成到电机系统中。同时具有耐高温、耐潮湿、抗震动等优点。被广泛用于航空航天、军事、电动汽车等领域。
通常建议使用与永磁电机相同极对数的旋转变压器[2],以使电机具有更好的电子换相和获得更高的传感器精度。但是实际上,并没有这么多与之对应的旋转变压器。同时,现有的文章中,大多是关于旋转变压器设计与信号处理的,很少有关于定、转子极数的配合。本文从采用正弦绕组的磁阻式旋转变压器工作原理出发,根据感应电动势,推导出定子齿数、绕组极对数和转子极对数之间的关系。再对10定子齿的旋转变压器进行有限元仿真,并制作样机进行试验。在此基础上,验证了极槽配合方法的可行性。根据所建立的关系,可以快速地设计出希望的旋转变压器。
1 磁阻式旋转变压器结构与工作原理
磁阻式旋转变压器是利用转子凸极效应,使两相信号绕组输出的感应电动势与转子转角成正余弦变化关系[3-5]。转子转过一周,输出电压变化周期数等于转子凸极数,因而旋转变压器的转子凸极数即为极对数。两相信号绕组输出电压具有相同幅值、频率,且对称布置,相位相差90°电角度。信号绕组输出的感应电动势为[7]
(1)
式中,ku为电压变比;U1为输入电压幅值;w为励磁频率;p为转子极对数;θ为转子转角。根据两相信号绕组输出电压包络线的正切值,即可计算出转子的位置信息。
磁阻式旋转变压器结构主要由定子、转子以及绕组组成。定子由开有齿槽的硅钢片叠压而成,而转子的外圆形状则设计成凸极结构[3]。其励磁绕组与信号绕组全部绕制在定子上。定子齿数为10,转子极对数为4 的旋转变压器如图1所示。

图1 磁阻式旋转变压器结构
励磁绕组主要采用等匝绕组,逐槽反向串联绕制在定子上,第i个定子齿上的励磁绕组匝数为
Nei=Nemcos(i-1)π
(2)
式中,Nem为励磁绕组匝数基数。
信号绕组主要采用等匝绕组或正弦绕组[4]。采用等匝绕组的旋转变压器,信号绕组隔齿反向串联绕制在定子上,其定子齿数与转子极对数之间满足Zs=2mp,其中m为信号绕组的相数[2],一般为2,即正余弦两相信号。第i个定子齿上的信号绕组匝数为
(3)
式中,Nsi为第i个齿上正弦信号绕组匝数;Nci为第i个齿上余弦信号绕组匝数;Nmax为正、余弦信号绕组匝数基数。
采用正弦绕组的旋转变压器,信号绕组匝数按正弦规律变化绕制在定子齿上,两相匝数之间相差90°电角度。第i个定子齿上的信号绕组匝数为
(4)
式中,pw为信号绕组极对数,θ0为常数。
2 磁阻式旋转变压器极槽配合
根据励磁绕组绕线方式,若忽略高次谐波含量,第i个定子齿下的气隙磁通为[4][6]
(5)
式中,φ0为磁通恒定分量;φ1为磁通基波分量[3]。
与文献[4,6]不同,本文引入了信号绕组极对数pw来区别于转子极对数。两相信号绕组匝数计算公式如式(4)。根据励磁绕组的绕制方法,采用正弦绕组的旋转变压器,信号绕组有两种绕制方法。
第一种绕制方法是信号绕组与励磁绕组类似,绕制的方法为逐槽反向串联绕制。根据式(4)、式(5),定子齿间磁通、信号绕组间匝数将有2π/Zs相位差,正弦信号绕组感应电动势可以写成:
其中第一项为零,对第二项化简得:
(7)
由旋转变压器工作原理可知,p+pw或p-pw需是Zs的一个因子,即:
p±pw=KZs
(8)
式中,K为整数。此时,式(7)中的其中一项将为零,另一项为恒定值。正弦信号绕组感应电动势为
Us=2.22fZsNmaxφ1sin(pθ)
(9)
第二种绕制方法是信号绕组绕制方向为同一个方向。因此,偶数齿间的磁通与信号绕组间匝数有2×2π/Zs的相位差,奇数齿情况相同。此时根据信号绕组输出感应电动势同理可得:
(10)
综上,定子齿数Zs、信号绕组极对数pw和转子极对数p之间的关系可以写成式(10)。其中当K取偶数值时,采用第一种绕制方法,当K取奇数值时,采用第二种绕制方法。
式(10)计算出的一些极槽配合由于极对数过高,在实际设计制造中并不实用。本文选取K=0和K=1的两种情况进行研究,此时:p=pw或p=(Zs±2pw)/2,可以得到表1。当p=pw时,式(4)计算得到的正余弦信号绕组匝数应交替乘以(-1),以确定绕制方向。当p=(Zs±2pw)/2时,正余弦信号绕组匝数和绕线方向可以直接由式(4)确定。
由表1可以看出,信号绕组的极对数不一定等于转子极对数,同一个定子可以与不同极对数的转子配合。且信号绕组极对数越高,可以配合的转子极对数越高。因而在不改变定子尺寸的情况下,可以通过增加绕组极对数来增加转子极对数,以此提高旋转变压器的测量精度。当定子齿数一定时,不同极对数的转子可以共用同一套绕组结构,且两个极对数的和等于定子齿数。例如定子齿数为12,信号绕组极对数为2,转子可以选择极对数4或8。当p=pw且p=(Zs-2pw)/2,即Zs=4p,θ0=0或π/2时,信号绕组隔齿匝数相同,隔齿反向串联绕制在定子上,这即是等匝绕组。所以输出绕组采用等匝绕组的方式是采用正弦绕组的特殊情况。
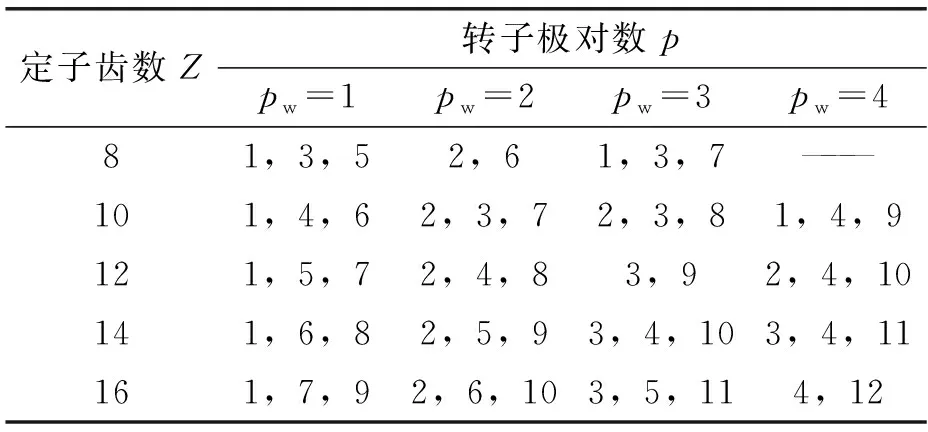
表1 旋转变压器极槽配合方法
3 仿真与实验分析
为了验证得到的定子齿数、转子极对数和信号绕组极对数之间的关系,本文以定子齿数Zs=10为例,由表1可知,信号绕组极对数可以设计成4种,如图2所示,定子齿上信号绕组匝数按正弦规律放置。不同极对数的信号绕组在同一定子齿上的匝数和绕制方向不同。绕组匝数的正负号即表示绕制的方向。
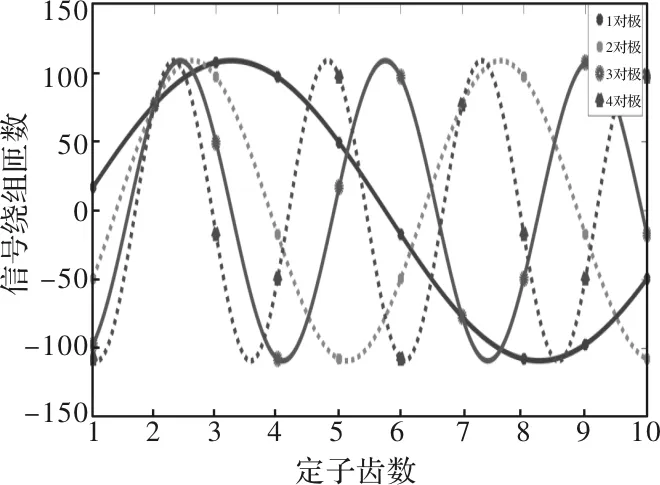
图2 不同绕组极对数下信号绕组在定子齿数的匝数分布
根据表1中定子齿为10的配合关系,建立旋转变压器模型,并进行有限元仿真[8],信号绕组输出电压如图3所示。

图3 定子齿数为10的旋转变压器仿真波形
由图中可以看出,两相信号绕组输出电压幅值相同,频率相同,且相互正交。同时,转子转过一周,输出电压变化周期数等于转子极对数,满足旋转变压器工作原理。由此也可以看出,第一种绕制方法是第二种绕制方法的一种。例如,pw=1,p=1的旋变与pw=4,p=1旋变相同。电压幅值如表2所示,Um为输出电压幅值。可以看出,当定子齿数、信号绕组极对数相同时,转子极对数越多,输出的感应电动势幅值越小,这是因为转子每极分配到定子齿数越小。

表2 定子齿数为10的不同旋变输出电压幅值
根据上文得到的配合关系,制作定子齿数为10、转子极对数为4、绕组极对数为1的磁阻式旋转变压器样机,并搭建实验平台,如图4所示。励磁绕组通入额定频率的电压信号,两相信号绕组输出电压的波形如图5所示。样机信号绕组输出电压幅值和频率相同,且相互正交。因此,本文推导出来的极槽配合方法是可行的。

图4 试验平台
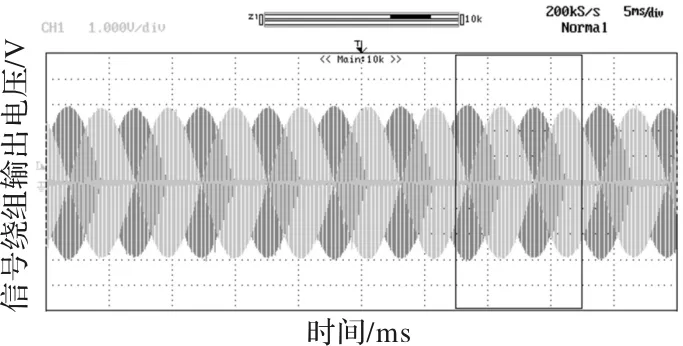
图5 旋转变压器样机输出电压波形
4 结 论
本文针对旋转变压器设计过程中如何选择极槽配合方式的问题,在绕组匝数计算中引入绕组极对数,从旋变的工作原理出发,根据输出感应电动势,推导出定子齿数、绕组极对数和转子极对数之间的关系。并进行有限元仿真和样机试验。结果验证了极槽配合方法的可行性,表明同一个定子可以与不同极对数的转子配合,不同的转子可以共用同一套定子和绕组形式,因而在不改变定子尺寸的情况下,可以通过增加绕组极对数来增加转子极对数,以此提高旋转变压器的测量精度。大大缩短旋转变压器设计时间,提高设计效率,也增加旋转变压器的种类,有利于旋转变压器产品的系列化。

