VAOS克里金插值在三维地震属性平面图的应用
王美琪 李 建
(西南石油大学计算机科学学院 四川 成都 610500)
0 引 言
克里金插值法是一种在地统计学中常用的空间插值方法[1]。该插值方法最优无偏,效果优于距离加权法和趋势面法,目前已应用于许多领域,几乎是20世纪中后期以来应用最为广泛的地理空间插值方法[2],如地质学、土壤学、生态学、气象学、遥感甚至其他研究“时空变量”的领域[3-5]。克里金插值法主要分为两大部分:(1) 量化已知数据的空间相关性即变差函数,一般来说,距离较近的点属性值越接近,距离较远的点属性值相差较多;(2) 确定邻域范围并搜索邻域点,确定克里金方程组,求解克里金方程组得到权重系数,利用权重系数加权求和得到待插值点的属性值。
在石油行业中,通过提取三维地震目的层的属性数据[6],计算得到属性数据的分布平面图,如振幅、频率、属性聚类等含油气预测平面图,为找油找气提供目标方向。三维地震属性平面图的形成需要插值,由于三维地震属性数据巨大,在实际应用中难以全区域计算,一般采用局部邻域为每一个待插值点搜索出合适的邻域点作为输入。目前邻域点搜索多采用指定半径的圆或椭圆,将在圆或椭圆内的点作为邻域点输入,该方法须遍历,并计算所有已知点到待插值点的距离。文献[7]漂移模式和搜索范围参数的影响较小,可忽略不计;文献[8]改进了邻域克里金插值法;文献[9]采用Delaunay三角划分搜索和固定距离的方式搜索点;文献[10]引入KD-Tree的二维索引结构,提出改进J邻近点搜索方法,效率有所提高,但该类搜索仍需计算已知点到待插值点的距离,这无形中增加了计算量。本文提出了一种无须距离计算、无须遍历已知点而直接利用待插值点位置的增减实现邻域点的选取算法,快速实现克里金插值。经过实验证明,在同精度下,该算法比指定距离半径的圆或椭圆搜索算法快,特别对于海量数据,该算法更显优势。
1 VAOS基本原理
数据插值是通过已知邻近数据点获得未知数据点,使数据规则化、网格化的过程。如何快速确定待内插网格点周围的已知邻近数据点是提高克里金插值效率的关键。
1.1 坐标到网格的转换
假设空间数据点的坐标为P(x,y,z),可转换为网格位置P′(ndx,ndy,ndz)来表达,n为网格数,dx、dy、dz为网格间距。将已知数据坐标统一到待插值网格,通过待插值网格位置的增减毫不费时找到已知点P(x,y,z),如图1所示。而已知点原始位置未变,不影响计算,因坐标转换取整有可能几点成为同一点,说明这几点相近。
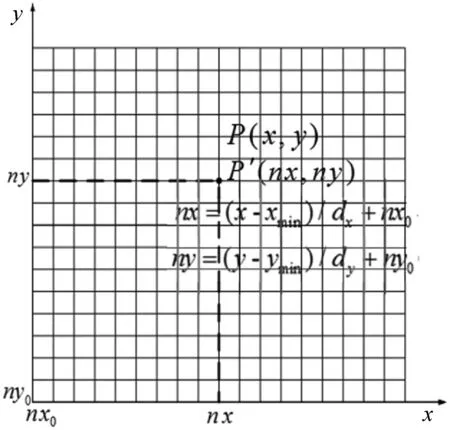
图1 坐标网格统一
假设:(1) 已知点平面位置表示为P(x,y),x、y最小值分别为xmin、ymin;(2) 待插值点网格方向x、y起始位置表示为nx0、ny0;(3) 待插值点方向网格步长表示为dx、dy。
则已知点P(x,y)在待插值点的网格位置可表示为P′(nx,ny),其中:
已知点统一到在待插值网格位置后,只需通过插值点网格位置的增减查找已知点,而已知点的原始位置并未变化,参加克里金插值时不受影响。
坐标到网络转换的伪代码如下:
输入:已知点P(x,y)个数为N;待插值点网格方向起始位置表示为nx0、ny0,待插值点方向网格步长表示为dx、dy。
(1) 已知点N中找到最小的x、y值xmin、ymin。
for (i=0;i { x>xmin;xmin=x; //最小的x y>ymin;ymin=y; //最小的y } (2) 已知点转换为待插值得网格位置nx、ny。 for (i=0;i { nx=(x-xmin)/dx+nx0 ny=(x-xmin)/dx+nx0 flag(nx,ny)=1 //标示该位置有已知点值 } 假设搜索的待插值点为w(i,j),如图2所示。 图2 邻近点搜索算法 (1) 待插值点w(i,j),x、y方向网格位置为i、j。 (2) 待插值点w(i,j),x、y方向增减网格总数nbx、nby。 (3) 待插值点w(i,j),x、y方向网格间距ndx=1,ndy=1。 (4) 待插值点网格x、y方向起始位置表示为:nx0=0,ny0=0。 (5) 待插值点x、y方向终止位置表示为:nxn,nyn。 则待插值点w(i,j)已知邻近点的搜索范围实际变为由i-nbx、i+nbx、j-nby、j+nby网格构成的边长为2nbx、2nby的四边形。判断四边形内的P′(nx,ny)是否有数据。 这样通过待插值点下标位置变量(i,j)的增减循环快速实现对所有待插值点邻近已知点的搜索。该过程伪代码如下: //为所有待插值点搜索邻近已知点 for (i=0;i //x方向位置变化 { for (j=0;j //y方向位置变化 { //为待插值点w(i,j)搜索邻近已知点 //设邻近已知点:N=0 for (m=i-nbx;m //i方向 //判断从i-nbx到i+nbx范围 { m<0 //进行下次循环 m>nxn //进行下次循环 for (k=j-nby;k //j方向 //判断从j-nby,j+nby范围 { k<0 //进行下次循环 k>nxn //进行下次循环 如P′(m,n)有数据n=n+1; } } //克里金插值 } } VAOS算法流程如图3所示。 图3 VAOS算法流程 为验证本计算方法,用实际三维地震属性数据进行插值,并与传统指定距离半径搜索邻近域克里金插值算法、Surfer软件插值算法[11-12]的结果进行对比。 该工区主测线290-420(131条),联络线320-400(81点),样本点数总点数为N=131×81=10 611,待插值网格点数为M=200×200=40 000。 (1) 效果图对比。三种算法插值的效果图对比如图4所示。 (a) Surfer插值结果 (b) 距离半径 (c) VAOS方法图4 算法插值效果 (2) 时间、复杂度对比。距离半径搜索算法:进行一次最邻近点w(i,j)搜索的时间复杂度为O(N),并计算待插值点到N点距离,并判断是否在距离半径内,本次半径距离为3,获得的邻近已知最小5个点,最大12个点,插值时间为135.6 s。VAOS搜索算法:进行一次最邻近点搜索的时间复杂度为O(nbx×nby),不需要计算待插值点到N点距离,只需要判断是否有值。本次给定nbx=3,nby=3,获得的邻近已知最小5个点,最大12个点,插值时间为2.79 s。 表1 算法插值时间对比表 预测目的层如图5(a)所示;提取振幅、频率等多种属性进行聚类,本文算法克里金插值绘制油气预测结果图如图5(b)所示。 (a) 预测目的层 通过对实际三维地震属性数据插值效果图、时间和复杂度进行对比,可以看出:插值的效果图基本一致,距离半径搜索算法复杂度远高于VAOS搜索算法和Surfer,指定距离半径搜索算法需遍历所有已知,并涉及距离计算,十分费时。VAOS算法无须距离计算、无须遍历已知点,直接利用待插值点位置的增减实现邻域点的选取,速度极快。 VAOS算法将遍历数据搜索算法变为图像位置的增减可谓是一个创新,该算法搜索速度快,实用性强。1.2 待插值点位置的增减搜索邻域点算法
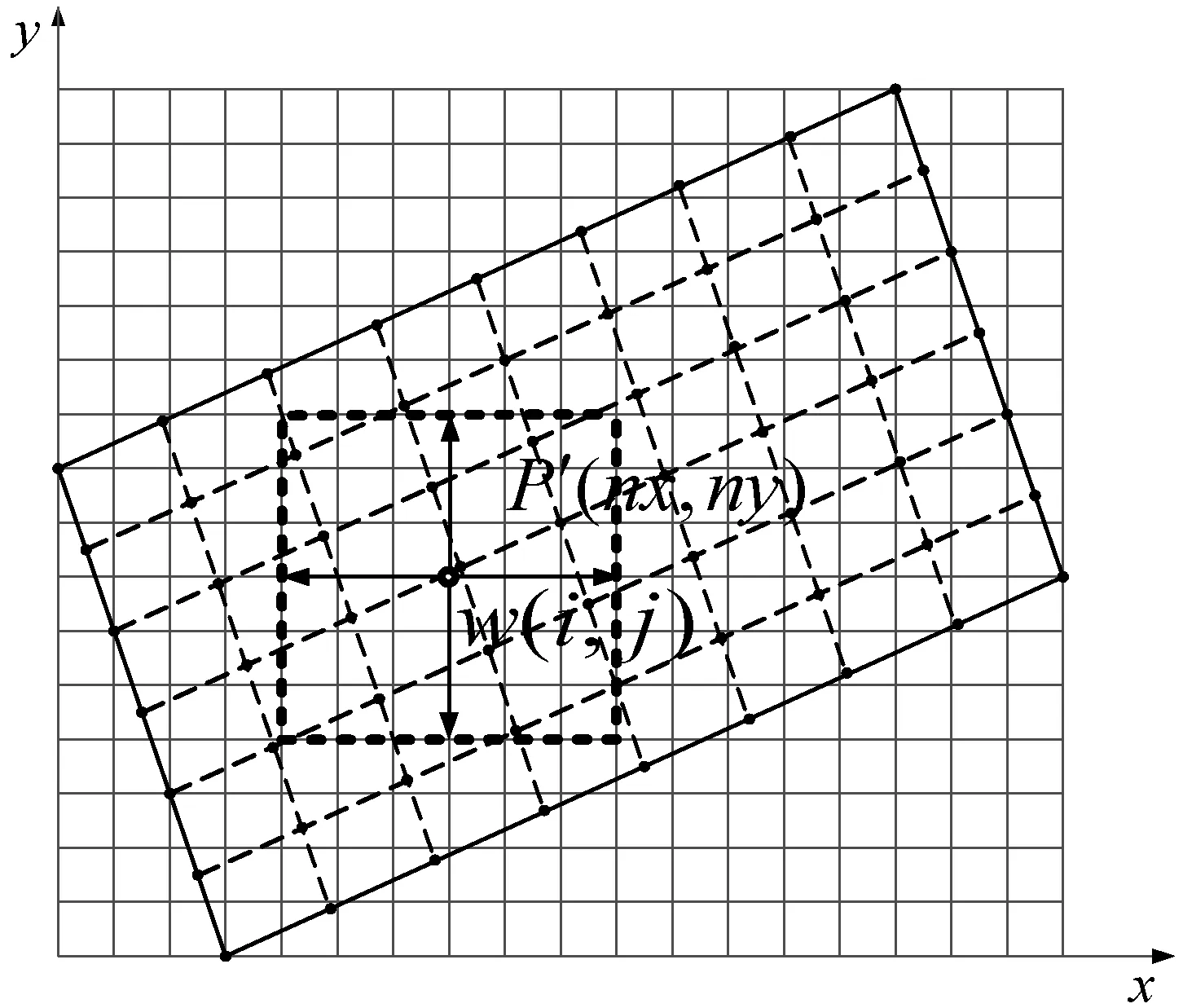
1.3 VAOS算法流程
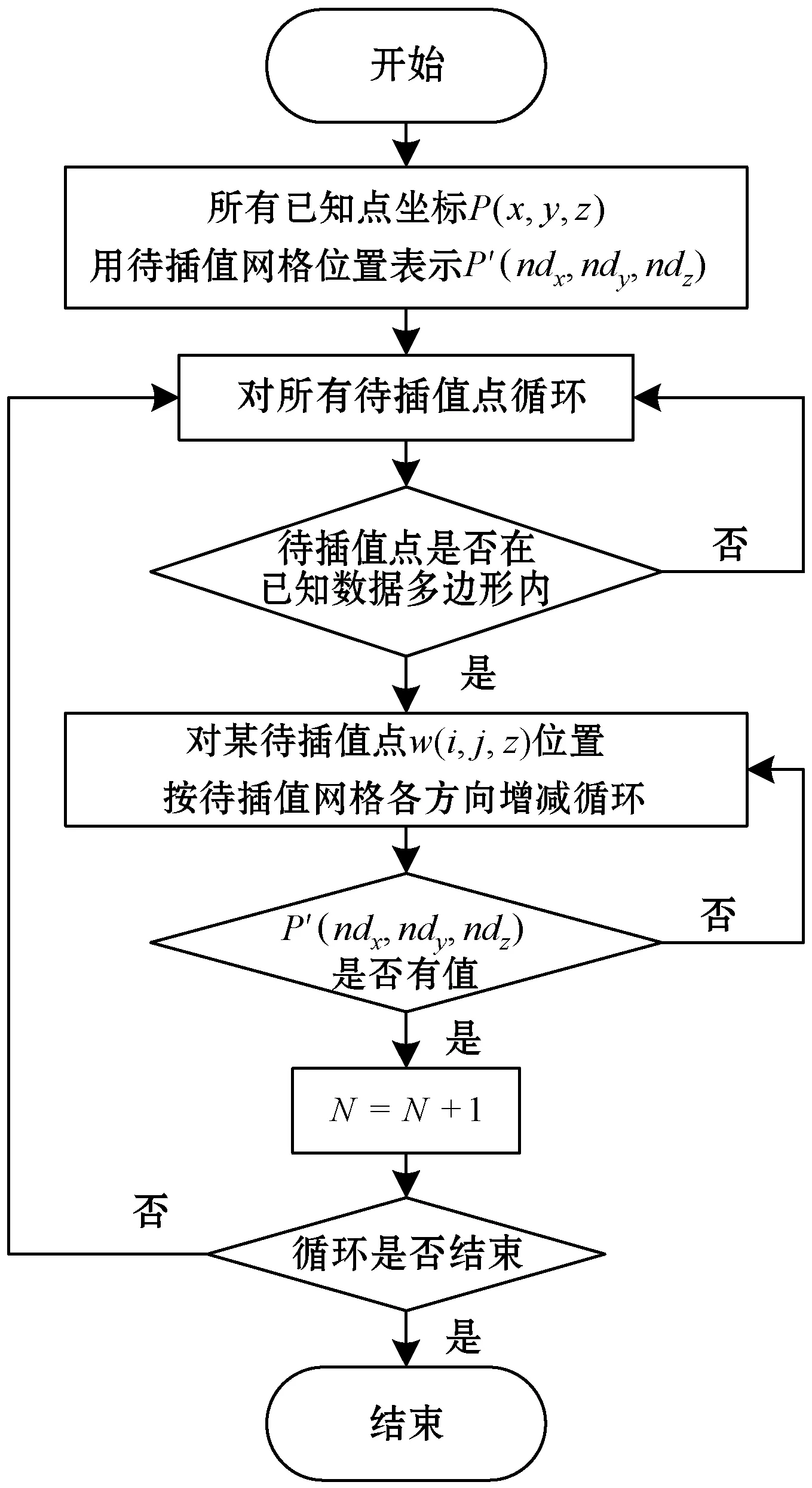
2 验证与应用
2.1 对比分析验证
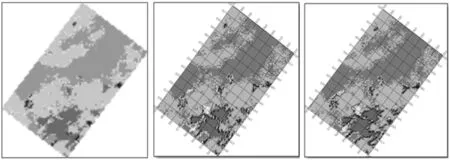

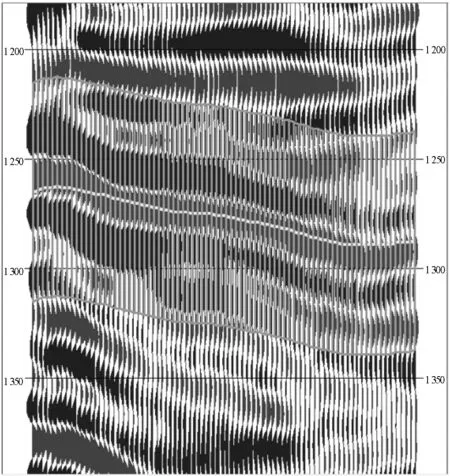
2.2 三维地震油气预测应用
3 结 语

