数列教学中应把握的几个核心

◇ 山东 宁俊平

数列的有关内容是考查考生观察分析、化归转化、推理论证等能力的有效载体,因此数列成为高考试题的主干内容．本文对数列教学应把握的“核心”进行举例说明．

1 核心知识

数列模块中的核心知识主要包括:等差和等比数列的定义、通项公式、求和公式、数列的性质等．

1){an}为等差数列,m,n,p,q,t∈N∗,若m ＋n＝p＋q＝2t,则am＋an＝ap＋aq＝2at．同理,若{an}为等比数列,则有aman＝apaq＝

2){an}为等差数列,即an＝a1＋(n－1)d＝dn＋(a1－d),当d＞0 时,{an}单调递增;当d＜0 时,{an}单调递减．若{an}为等比数列,当a1＞0,q＞1,{an}单调递增;当a1＜0,q＞1,{an}单调递减．当a1＞0,0＜q＜1,{an}单调递减;当a1＜0,0＜q＜1,{an}单调递增．

2 核心问题

问题1求数列的通项公式

1)已知数列类型(等差或等比)求通项公式,可采用基本量法求解,即通过所给关系列出方程或方程组求解即可．

2)已知数列的前n 项和求通项公式,可利用an＝Sn－Sn－1(n≥2)求解,注意对n＝1进行检验．

3)给出递推关系求通项公式,主要是用迭代、构造等方法将一般数列转化为特殊数列(等差或等比)．

例1设{an}的前n 项和为且当n≥2时,4Sn＋2＋5Sn＝8Sn＋1＋Sn－1．

(2)求数列{an}的通项公式．

(1)将4Sn＋2＋5Sn＝8Sn＋1＋Sn－1进行拆项构造可得

即4an＋2＋an＝4an＋1,再进行拆项构造得

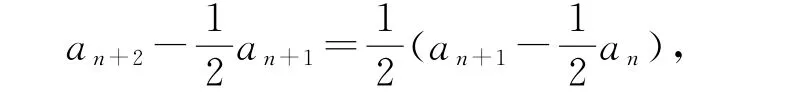
问题2求数列前n 项和的方法

1)对于“等差±等比”型,利用分组求和法．分别利用等差、等比数列求和公式求和,再相加或相减即可．对于“等差×(÷)等比”型,利用错位相减法．

2)若所求和的数列满足a1＋an＝a2＋an－1＝a3＋an－2＝…,可用倒序相加法求和．

例2已知{an}的前n 项和Sn＝3n2＋8n,{bn}是等差数列,且an＝bn＋bn＋1．

(1)求数列{an},{bn}的通项公式;

解析(1)an＝6n＋5,bn＝3n＋1(求解过程略)．

(2)由(1)可知

由①－②,可得

所以Tn＝3n·2n＋2．

例3已知{an}的通项公式为an＝n2,设的前项和为Sn,求证

证明因为an＝n2,所以则

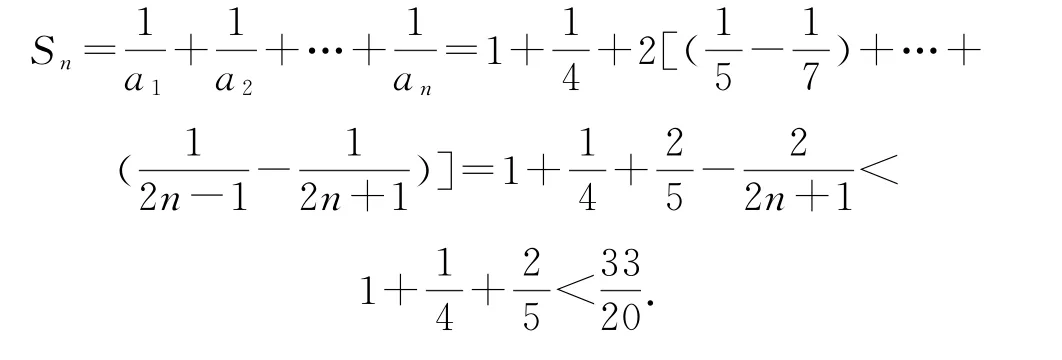
3 核心思维

因数列的规律性较强,所以在处理数列问题时,所涉及的核心思维是关注数列的项数、准确判断数列的属性．另外由于数列中的各项与其项数之间存在一一对应的关系,因此在处理某些数列问题时,可利用函数的思想来认识、理解数列,进而解决问题．

例4已知数列{an}的通项公式为an＝lnn,若存在p∈R,使得an≤pn 对任意的n∈N∗都成立,则p 的取值范围是_____．

解析因为n∈N∗,所以an≤pn,即因此问题转化为求的最大值．设求导得令f′(x)＝0,得x＝e．所以在(0,e)内,f′(x)＞0,f(x)单调递增;在(e,＋∞)内,f′(x)＜0,f(x)单调递减．的最大值在n＝2或n＝3处取得,进而只需比较的大小即可．由的单调性可知所以p 的取值范围是