放缩取点法在讨论函数零点问题中的应用

◇ 山西 赵海涌

利用导数求解与函数f(x)零点有关的综合问题,是近几年高考中的热点题型．求解这类问题大多需要用到零点的存在性定理,这就需要在函数的定义域内取定两个点x1,x2,不妨设x1＜x2,并且使得f(x1)f(x2)＜0,进而确定f(x)在区间(x1,x2)内有零点．然而,满足f(x1)f(x2)＜0的两个点x1,x2的取法,有时较为复杂．本文介绍“放缩取点法”,可以较好地突破这一难点．

例1已知函数f(x)＝(x－2)ex＋a(x－1)2(a＞0),试讨论f(x)零点的个数．

解析f(x)的定义域为(－∞,＋∞),f′(x)＝(x－1)(ex＋2a)．容易看出ex＋2a＞0,所以,当x∈(－∞,1)时,f′(x)＜0,故f(x)在(－∞,1)单调递减;当x∈(1,＋∞)时,f′(x)＞0,故f(x)在(1,＋∞)单调递增．fmin(x)＝f(1)＝－e＜0．

由函数单调性可知f(x)在(－∞,1)上至多1个零点,在(1,＋∞)上至多1个零点．由于f(2)＝a＞0,则f(1)f(2)＜0．根据零点存在性定理可得函数在(1,＋∞)上有唯一零点．当x＜1时,因为(x－2)ex＞(x－2)e,故f(x)＝(x－2)ex＋a(x－1)2＞(x－2)e＋a(x－1)2．

令(x－2)e＋a(x－1)2＝0,即a(x－1)2＋e(x－1)－e＝0,

综上所述,当a＞0时,函数f(x)有2个零点．

点评x0的确定,我们利用了放缩法,即当x＜1时,(x－2)ex＞(x－2)e．事实上,令g(x)＝(x－2)ex－(x－2)e,即g(x)＝(x－2)(ex－e),则g′(x)＝ex(x－1)－e,当x＜1 时,g′(x)＜0,故g(x)在(－∞,1)上单调递减,g(x)＞g(1)＝0,所以(x－2)ex＞(x－2)e．如果感觉这样取点x0比较复杂,那么我们就可以调整放缩．

例如,当x＜1 时,(x－2)ex＞－e,故f(x)＝(x－2)ex＋a(x－1)2＞－e＋a(x－1)2．

令－e＋a(x－1)2＝0,解得这样取得的x1要比上面的x0简单．此时也有f(x1)·f(1)＜0,函数f(x)在(－∞,1)内有唯一零点．

放缩取点法的本质是根据函数解析式中的某部分的单调性进行局部放缩．例如,f(x)＝(x－2)ex＋a(x－1)2＞－e＋a(x－1)2,实质上是利用函数h(x)＝(x－2)ex在(－∞,1)上单调递减,直接把(x－2)ex缩小为在x＝1处的函数值h(1)＝(1－2)e＝－e．

例2讨论函数的零点个数．

解析f (x) 的定义域为 (0, ＋ ∞),

当a≤0时,f′(x)＜0,f(x)在(0,＋∞)单调递减,并且因为a≤0,并且0＜x＜1时当且仅当a＝0时,取等号,故f(x)＝解得所以f(x0)≥0,故f(x0)f(1)≤0．根据函数零点存在性定理可知,函数f(x)在(0,＋∞)内有唯一零点．

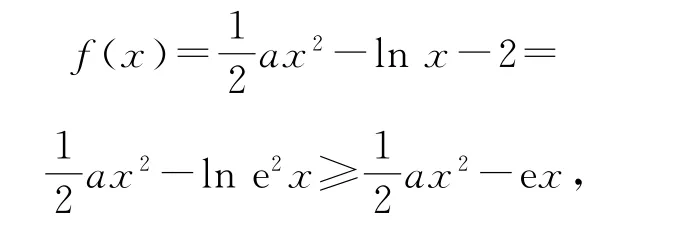
综上所述,当a≤0,或a＝e3时,函数f(x)在(0,＋∞)内有唯一零点;当0＜a＜e3时,函数f(x)在(0,＋∞)内有2 个零点;当a＞e3时,函数f(x)在(0,＋∞)内无零点．

点评当时,对f(x)的放缩,利用了lne2x≤ex．事实上,我们设g(x)＝lne2x－ex,则得0＜x＜所以gmax(x)＝,故g(x)＝lne2x－ex≤0,即lne2x≤ex,因此时,取等号)．