短跑的多重运动与多重运动规律拓展

哈尔滨理工大学理学院 黑龙江 哈尔滨 150080

前言

鉴于经典力学长时间将自由度与运动维度相提并论等因素,现用短跑多重(chong)运动代替初探短跑时提出的短跑多维运动。亦是研究进入新领域的需要。本文强调成功绘制的关键——随行逼近拍测法。深入认知短跑运动图线特点,给出各重速度增量时间图线,认识各重速度增量地等值关系,进一步说明用三四重机械运动规律解析短跑运动可行。并将多重观拓展至一般力学领域。

1 多重运动研究对象

(1)机械运动的四个重度：平动；转动；耗散运动(摩擦、粘滞、形变等将动能转化为非机械能的运动形式)；源动力运动(含内能转化动能、生化能转化动能、电能转化动能等机械运动)。运动重度不与运动维度一一对应。这是引入运动重度的根本原因。耗散运动导致生物体运动中动能损耗。而导致损耗的多种因素归结到一个运动重度——耗散运动。

(2)多重运动理论研究对象是刚体为主的刚体、非刚体、动力装置等的复合体。运动员是集三种特性为一身的复合体。

2 短跑的三四重运动

(1)研究短跑运动图线,分前后支撑两阶段。受短跑前后支撑对应的水平摩擦力冲量比为50 kgm/s/69 kgm/s近似等于3/4启发,受短跑是无滑动滚动启发,提出侧面观测的短跑是三四重(之前称三四维)运动。短跑前支撑的三重动能定理、三重动量定理表达式顺次是

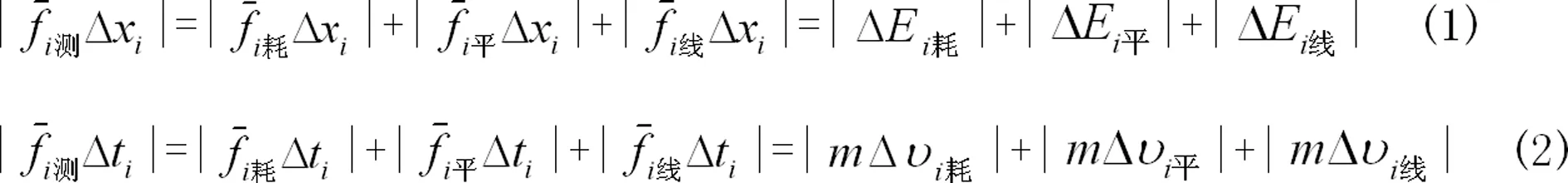
短跑后支撑的四重动能定理、四重动量定理表达式顺次是

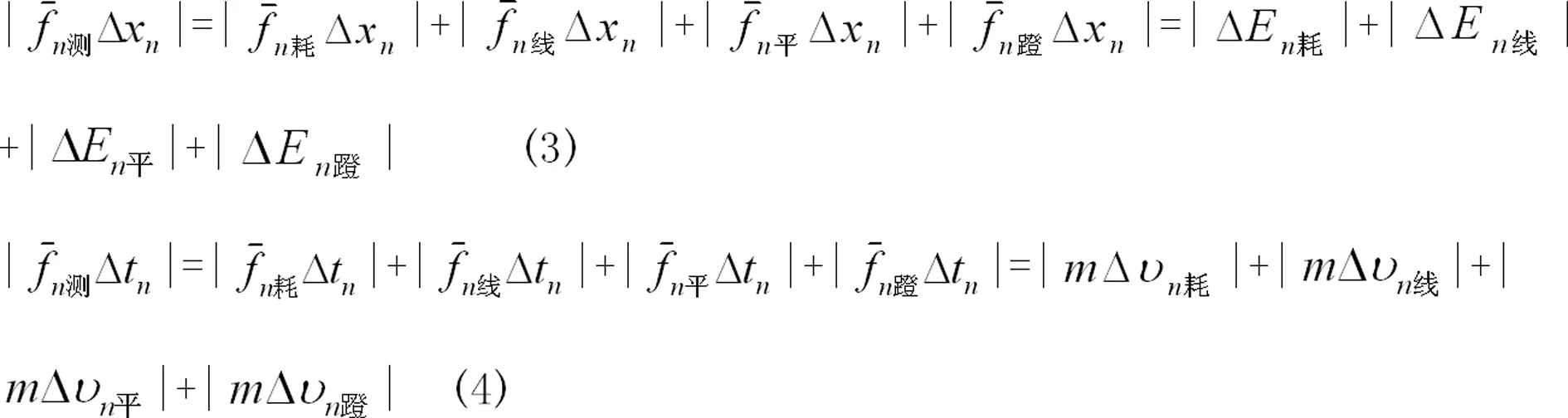
图1表明,后支撑任意小时段人体受反向力偶矩。二式中前两项都与转动相关,蹬伸导致部分前支撑遗留的线速度损耗,部分前支撑遗留的线速度逐步转化为后支撑的平动速度。上诉各关系式长期存在问题：前后支撑‘各小段位移速度增量相等吗?精度如何?’

3 短跑多重运动地增量图线分析法

图2上部曲线为途中跑支撑时段运动员受的水平摩擦力时间图线。即f测-t图线。其中部水平线为时间轴。其下面曲线υ腾ABK为X轴速度图线。它们源自短跑测试图线。曲线υ腾ABK(本文将其竖直向放大数倍)是跑台测试法绘制：拍测时高速摄像机主光轴尽量接近运动员质心(提高精度),运动员脚着皮带前,人体质心及高速摄像机对皮带的水平平动速度为υ腾(测试时皮带对地以速度υ腾向后运动),线速度为0(无转动)。前脚着带前高速摄像机光电装置测力装置同步开始测试,着带瞬间开始推算。依运动员各环节质心坐标给出开始时刻人体总质心坐标,依高速摄像机系列图像推得总质心的后续系列坐标。对应观测法称为随行逼近拍测法。前支撑时段运动员受反向水平摩擦力(图2水平线下部的摩擦力),致使前支撑运动员质心相对皮带的水平位置逐渐落后(前支撑时段观测的系列水平位移增量为负),质心相对皮带的平动速度逐渐减小(系列平动速度增量为负)。这种观测方法关键在于能精确观测人体损失的平动位移增量、平动速度增量(观测涉及人体总质心、摄像机主光轴在观测面投影点的相对运动,这时只涉及人体平动)从而绘制出υ腾ABK段平动速度曲线。

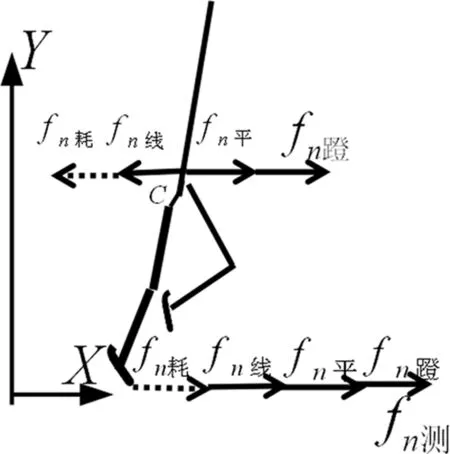
图1 后支撑受力分析

(1)依式(2),前支撑三重运动涉及Δυi耗、Δυi平、Δυi线三个速度增量。图2υ腾K可视为地面上摄像机相对皮带以水平平动速度υ腾匀速运动速度图线。其坐标系为υOt。该图象坐标原点为(O、0),在下述运动图象中排序第一。该图线起点对应线速度为0(着带前运动员无转动)。前支撑任意时段质心的-Δυi耗增量时间图象坐标原点(υ腾、0),速度轴υ腾υ向上为正方向,时间轴υ腾T对应时间标记与0tA段时间的标记相同。任意时段,从速度图线上部任取一小段速度图线Δγi耗在速度轴的投影为损耗的速度增量-Δυi耗,负的增量累加得图2下行损耗速度增量时间曲线υ腾A。TA对应前支撑平动速度的总损耗-Δυ前耗(对应前支撑损耗的总位移,等于υ腾TA的面积值)。任意时段从速度图线下部任取一小段速度图线Δλi在速度轴的投影为平动速度增量-Δυi平,其增量时间图象坐标原点(υ腾、0),速度轴υ腾υA向上为正方向,时间轴υ腾T对应时间的标记与0tA段标记相同。υ腾υAA区域的TA对应前支撑平动速度因转化而减少的总量-Δυ前平(对应前支撑平动减少的总位移,等于υ腾υAA面积值)。-Δυi耗、-Δυi平变化趋势及量值完全相同,它们对应的二条速度增量图线重合为图2下行速度增量时间曲线υ腾A(该曲线具有两面性,该图线可一分为二,排行二、三)。前支撑时段,短跑在无滑动滚动中,减少的平动动能逐渐转化为等量的转动动能,有-Δυi平=+Δυi线。所以质心的线速度增量Δυi线时间图线与图2前支撑平动速度增量时间图线υ腾A呈镜像关系。+Δυi线为对应的一小段线速度图线Δρi在线速度轴υ腾υA上的投影。用镜像法得υAT段上行线速度增量时间曲线,其坐标原点(υA、0),对应线速度0点。向上为正方向(对应图线排行第四),A T对应前支撑线速度总增量+Δυ前线(对应前支撑线速度的总位移,等于υATA面积值)。依图2二、三、四号增量时间图线,时刻有|Δυi耗|=|Δυi平|=|Δυi线|,对应的有|Δxi耗|=|Δxi平|=|Δxi线|,才使得三条图线可共处一图。由于前支撑是三重运动,线速度增量时间图线不具两面性。前支撑任意时段,摩擦力测使三重运动的状态发生等量变化,故得式(1)式(2)。这是首次依速度增量时间图线给出式(1)式(2)。

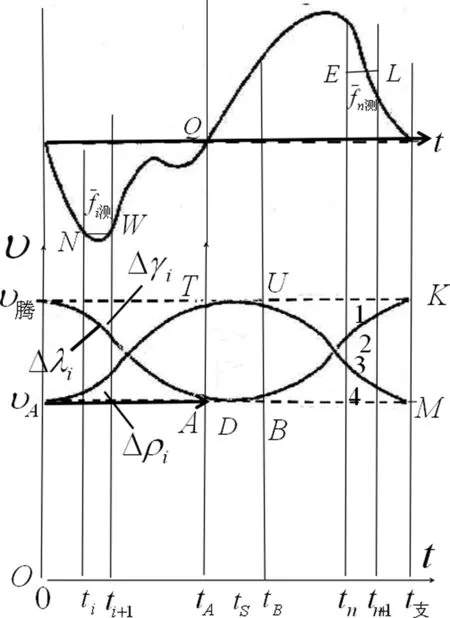
图2 复合速度图线与关联分析

(2)后支撑包括过渡与发力两个阶段。实测表明过渡阶段(tAtB时段)运动员并未蹬伸。过渡阶段动力是运动员依转动惯性前摆,身体重心降低等提供。后支撑蹬伸动力源包括这部分动力。蹬伸使后支撑为四重运动。蹬伸提供的动能在四重运动均分。高速摄像机拍摄的系列影像反映后支撑时段质心相对皮带的速度逐渐增大。对应的平动位移增量、速度增量都是正的,反映蹬伸对运动员平动速度等地补偿。后支撑时段的反向力偶矩则起反作用。依式(4),后支撑四重运动涉及Δυn耗、Δυn蹬、Δυn平、Δυn等效四个速度增量。TA对应前支撑平动速度总增量-Δυ前平。Δυn蹬与+Δυn平同步,二者与-ΔυA前平合成ABK段上行平动速度增量时间曲线。或者说二图线起于坐标原点(A、tA),向上为正。在TABK区域(1区)看ABK速度增量图线任意小段对应的是速度增量+Δυn蹬。在ABMK区域(2区)看任意小段速度图线对应的是平动速度增量+Δυn平。二增量为正,补偿平动速度。-Δυn等效、-Δυn耗加上前支撑时段转动遗留的顺时针线速度+Δυ前线(对应T点),三者合成的线速度增量时间图线与ABK段上行速度曲线反相。用镜像法得TUM下行线速度增量时间曲线,其原点坐标(T、tA)(轴线TA对应tA瞬时线速度值,向上为正方向。在TUKM区域(3区)看线速度图线任意小段在线速度轴线TA上的投影是线速度增量-Δυn等效,它等于对应时段前支撑遗留线速度的减少量(转化为Δυn平)。在TUMA区域(4区)看线速度增量图线任意小段在线速度轴线TA上的投影是线速度增量-Δυn耗。ABMK包围的面积值等于后支撑时段-Δυn耗的总损耗,实为对应前支撑遗留线速度的总损耗(蹬伸阻碍顺时针转动),其总值等于TA。-Δυn耗、-Δυn等效、+Δυn蹬、+Δυn平四个增量等值,它们对应的各位移增量也等值。四个增量对应四条增量时间图线。后支撑任意时段,摩擦力测使四重运动的状态发生等量变化,故有式(3)式(4)。结果表明,式(1)式(2)式(3)式(4)都是精准关系式。这表明,复合图线分析法与多重运动规律匹配；随行逼近拍测法与短跑运动图线匹配。随行逼近拍测法测试过程拍摄的运动员影像,一是支撑时段影像排列的情况：中间疏两边密。这段对应时长等于支撑时长,这段长度对应支撑时段位移。二是腾空时段运动员影像的质心重合,只能从影像看到各环节的摆动。

场地拍测法得到系列近似等距排列的运动员影像。依腾空时段运动员质心通过的位移和用时可求出运动员X方向的腾空速度υ腾；依支撑时段运动员质心通过的位移和用时可求出支撑时段运动员质心X方向视速度的平均速度。视速度是平动速度与线速度合成的速度。场地拍测法得到的是两种速度,二速度关系尚未知,不能共图(线速度占比小,近似计算可共图)。场地拍测法与短跑运动图线不匹配。场地测试数据不能直接检验跑台测试数据。

依短跑腾空速度10 m/s(与短跑测试图线对应的腾空速度非常接近)推算,短跑前支撑时段平动速度总波动量约0.21 m/s。依短跑前支撑三重运动的平动动量改变总量对应前支撑总冲量的三分之一,数值上有mΔυA前平/50 kgms-1=1/3,得被测运动员质量m=79.4 kg。与优秀短跑运动员质量非常接近。再次证明多重运动规律解析短跑途中跑运动可行。

4 一例二重机械运动的观测与解析

一长方形木块质量为m,用同一推动装置使一较大木块和高速摄影机以水平初速度υ0并行。木块全部滑上测试水平面(测试平面上有刻度,木块上有光电同步拍测装置)滑道,撤掉对木块的推力,开始测算。观测过程高速摄影机始终以水平初速度υ0并行。观测时还用置于水平面下的测力板测量木块运动时受的水平摩擦力,通过fOt坐标系绘出水平摩擦力时间曲线,图3上部近似与时间轴0t平行且略波动的图线示意。高速摄像机主光轴与木块上一标志点等高(由于观测木块平动,可取其上任意点为标志点,但一般情况下应尽量对着质心)始终以υ0匀速前进。木块沿测试水平面运动时,观测记录标志点不断落后产生的损耗位移增量-Δxi耗,推算损耗速度的系列速度增量-Δυi耗,绘制出损耗速度增量时间图线。见图3线段υ0t下面的υ0A段曲线(该曲线与向下的系列箭头对应)。该图线具有两面性。该图线在υ0υAA区域对应的平动速度增量为-Δυi平。且任意时段有Δυi耗=Δυi平。

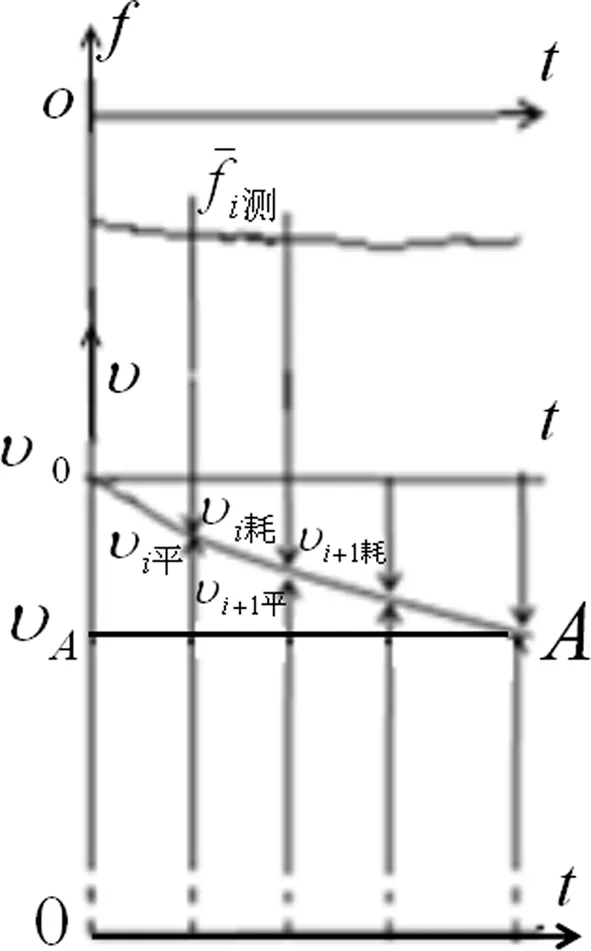
图3 二重速度图线

显然Δti段实测合力在两重运动的二分力相等,即对任意小时段。式(5)是摄像机以υ0速度跟拍观测结果的关系式。改变接触面光滑度,测试绘制的速度增量时间曲线的斜率有会有变化,但对应规律不变,仍可用式(5)形式表示。式(5)是此类二重机械运动动量定理表达式。水平线段υ0t对应的匀速直线运动是一重机械运动,只涉及木块的平动。再作一件事：求任意时段木块的平均平动加速度平,将其乘以木块质量得。实测得这样结果能深入认识υ0A段曲线的两面性。

雪地摩托沿平地无动力滑行为二重运动。其加速运动为三重运动。这里的重度显然与维度不同。初中物理用弹簧秤测摩擦力实验是平动振动耗散运动三重运动。目前尚无法解。

各种车辆整体都可视为复合体。可从各种简单电动车入手探索多重运动规律的应用。因为电动车便于进行各种测量。

5 初步结论

(1)随行逼近拍测装置方法是研究多重运动地保证。随行逼近拍测法与短跑测试图线匹配。

(2)多重运动规律适用于以刚体为主体的复合体。

(3)依机械能转换特点将复合体机械运动分为平动、转动、耗散运动、动力运动四个重度。

(4)多重运动规律不止适用于途中跑,还适用于解析一些力学问题。

(5)探索复合体多重运动是跨学科基本力学规律探索。做相关力学实验可精确测量检验。

(6)多重运动复合图线是剖析多重运动地好方法。能揭示复合体任意时段各种增量的等值关系。复合图线分析法与多重运动规律匹配。

(7)给出随行逼近拍测法与场地拍测法的影像区别。便于对照检验。

几十年前就有力学工作者对短跑运动进行整体观测,得到短跑运动图线。但少有深究。长期剖析短跑运动图线,初步明确短跑运动是多重运动,并初步给出多重运动规律。使全面测试短跑运动,智能分析短跑运动成为可能。

多重运动规律还可用于解析一些力学复合体运动问题。可进一步拓展多重运动规律的应用。力学相关实验可测的更准确。从而可探究复合体各成分占比等问题,可探究多重运动规律适用范围。目前多重运动规律尚系科学猜想,需要多方实验检验。