基于高中数学一题多解的学习研究

张鼎峰

(甘肃省敦煌市敦煌中学 736200)

一、基于高中数学一题多解的应用价值

一题多解在高中数学教学中的应用价值，主要体现在以下两个方面：其一，培养学生思维的灵活性.思维的灵活性基于思维的广阔性，对于培养学生敏捷性、独创性、批判性思维具有重要辅助作用.思维的灵活性体现在学生可以紧跟事物变化来完成观点的更新，进而实现从多层次、多角度出发来看待和思考问题，以及使用多种方法来厘清思考问题的方向；灵活运用数学定理公理来解题，突破思维局限性的制约.其二，有助于发散性思维的培养.发散性思维体现在学生可以站在各种角度并使用各种方法来围绕同一个问题做出深入思考，并从各个方面找到具备多样化特点的答案；除此以外，发散性思维还是学生深化理解数学知识必备的思维条件.

二、一题多解在高中数学教学中的应用研究

1.创设教学情境，渗透变式思想

高中数学教学的精髓就是“问题”，在能够发现各种问题的前提下，才能促进对新知识的探究.高中教师应怎样在新授课中创设有效的问题情境呢？笔者认为，通常情况下，其一是由已知问题来衍生新的问题，其二则是引导学生根据实际生活来抽象出具体的教学内容.灵活应用一题多解的变式方法完成教学情境的创设，并围绕学生认知水平和“最近发展区”，科学使用问题来源，为学生建设具备梯度性的变式问题情境，促使学生能够积极自主探究新旧知识间的联系，通过已有知识来总结归纳出新的知识.此时，在教师创设的变式情境下，能够促使学生更加深入思考“为什么”“怎么办”，进一步为新授课的高效开展奠定坚实基础.

例如，在进行“充分条件与必要条件”的教学时，出于让学生自由发挥想象，积极探求问题本质，实现逻辑思维“一题多解”的目的，教师可结合学生现阶段的学习水平，给学生创设以下变式问题情境组：

(1)杨利伟作为我国登上太空的第一人，其具备的“身体条件优势”和其“成为宇航员”间有着怎样的关系？

(2)老师今天感冒了，我的感冒能不能好和我打针吃药有着怎样的关系？

(3)观察教室的照明系统，“开关闭合”和“灯泡亮”间有着怎样的关系？

2.动态探究，系统构建

在高中数学教学中，探究活动是串联整体教学流程的关键一环，既能引导学生学会质疑、反思，培养良好学习习惯，也能促进学生对新旧知识的衔接，增强学习体验.在具体教学中渗透变式探究教学，能够打开学生创新思维之门，不仅可以培养发散性思维，而且还能培养归纳、类比等数学思维，促使学生能够从多方位、全角度来看待、分析和解决数学问题，有针对性地引导学生通过“变”的现象发现“不变”的本质.

例如，进行“等比数列的求和公式”教学时，不仅要求学生娴熟应用相应公式，还要求学生扎实掌握“错位相减法”这一数列求和公式的推导方法.出于不断深化和拓展本章教学内容，以及夯实学生掌握“错位相减法”使用条件，熟练计算过程的目的，教师可依据有关变式教学的理论，逐步渗透“一题多解”和“多题一解”的教学方式，为学生创设具备梯度性的变式题组，从而培养学生数学思维，使其扎实应用解题技巧.

(1)试求y=x+2x2+…+nxn的和为多少.

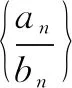
三、教学案例设计

在人教版高一数学上册130页中例4的学习时，笔者认为可带领学生深入挖掘，灵活运用等差数列前n项和公式及其性质，探究更多的解题方法，进一步实现一题多解的目标.

例4已知一等差数列前10项和为310，前20项和为1220，由此能确定其前n项和的公式吗？

分析一把已知条件代入等差数列前n项和的公式，可得到关于a1和d的关系，从而确定a1和d，最终得到所求前n项和公式.

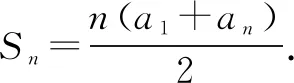
分析三因为{an}是等差数列，所以可设Sn=An2+Bn，此时再求A，B便可以了.

高中数学的一题多解就是启发学生在解题时进行更加深入的思考，灵活应用已知的性质公式，从而产生新的思想，促进学生思维的发散.最终促使学生真正明白，问题可能只有一个， 但是可以解决这个问题的思想方法却有千千万万种.

综上所述，一题多解在高中数学中的应用，需要教师关注学生在进行解题时如何实现对原有知识结构的二次认识，如何激发学习潜能的二次发挥；采取怎样的教学方式可以更好促进学生深入理解可推广的通性以及通法.总的来说，一题多解的应用需要教师做到因势利导、触类旁通，进一步落实培养学生数学素养的目标.