论高中物理中的电磁偏转问题

丁泽超

(安徽省宣城中学 242000)

静电场及磁场是高中物理知识学习的重点，也是考试中涉及的重点内容，一般情况下，考察学生带电粒子在静电场及磁场中的运动情况解析能力，对应的物理知识是电偏转及磁偏转内容.多数物理题目考察对象为带电粒子，两种偏转知识具有相似度，导致学生在解题过程中无法找到解题关键点，发生题目内容混淆问题，容易在解题时失分.一般情况下，两种偏转在物理规律及运动轨迹等方面存在一定差异，学生还需进行系统对比与分析，才能找到差异所在，明确解题思路，进一步提升解题准确性及解题效率.

一、电偏转问题

在高中物理学习过程中，电偏转内容主要是研究带电粒子运动轨迹及电偏转规律，为有效让学生掌握粒子运动轨迹及电偏转规律，可通过两个平行金属板及固定电压展开实验，比如，金属板的长度为l，电压值为U，将具有正电荷及电荷量为q、质量为m的粒子处于金属板间运动，其运动速度为v0，平行射入.粒子脱离静电场区域时，飞行速度为v，处于金属板垂直方向偏移距离为y，初始速度与飞出速度呈夹角，利用θ表示，该夹角便是电偏转后的偏转角.粒子进入电场后，在电场中呈现抛物线运动，对该运动方式进行分解，垂直金属板方向做匀加速直线运动，平行金属板运动方向则是匀速直线运动.带电粒子在电场中会发生偏转，在解题过程中，可先对物理量进行思考，并获得处理物理量的对应公式.在思考电偏转问题时，飞出速度v是重要条件，尤其是带电粒子在射出电场后速度延长线经过电场中心点.对此，还需对高中物理电偏转物理量关系进行分析，假设带电粒子射出电场区域的速度为v，电场与带电粒子速度反向延长线中心点是O1，带电粒子在运动过程中，射出电场区域时与该点位置水平方向距离为x，那么x的计算公式便是：

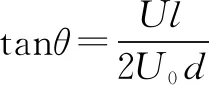
二、磁偏转问题

高中物理磁偏转问题在学习过程中，需认识到受力特点，质量m，电荷量q粒子在速度v0垂直进入匀强磁场中，感应磁场强度为B，受到洛仑磁力影响，获得F=BqV0，F方向一直与速度方向垂直，F只能够让粒子运动速度方向发生变化，速度方向变化会导致F方向发生变化.基础运动规律为，运动方向是持续变化的，若粒子在运动过程中，根据运动轨迹可分析圆的半径与周期.比如，在一个半径为R的绝缘筒中，顺着轴线方向匀强磁场中，磁场方向与纸面垂直向内，匀强磁场感应强度用B表示，圆筒磁场中边界是弹性材料.质量为m、电荷量为q的正离子在速度作用下顺着小孔M进入筒中，速度与半径θ是呈现30°夹角，与磁场方向垂直.离子与筒壁在接触后并未发生能量损失，若选择适当的进入速度，离子自M孔进入，那么离子速度多大，能够最短时间返回M孔？若离子与筒壁产生两次接触后自M孔射出，离子运动速率为多少？离子进入圆筒后返回M孔需要的时间是多少？

又比如，一个带电粒子进入匀强磁场，带电粒子在洛仑兹力下，发生运行偏转及磁偏转现象.带电粒子垂直进入均匀磁场后，速度为v，磁感应强度为B，可忽视重力影响，带电粒子在洛仑兹力作用下，展开匀速圆周运动，运动轨迹为圆弧.在运动过程中，带电粒子偏移量为y，水平位移距离是1，偏移角度为θ，周期为T，半径为r，角速度为ω，运动时间为t，各个物理量关系可通过以下关系表述：qvB=mv2/r=mω2r=m(2π/T)2r；r=mv/qB；ω=v/r=qB/m；t=Tθ/2π=θm/qB；T=2πr/v=2πm/qB.磁偏转实际问题解决过程并不复杂，学生在解答问题过程中往往综合思考圆形平面几何问题，导致解题难度增加.在实际解决磁偏转问题时，还需根据轨迹，找到运动规律，提升做题准确率.轨迹确定后，找到带电粒子圆周运动半径及圆心，可分为两种类型，分别是给出轨迹位置及方向，此情况下，连接两点做垂线，从而确定圆心.题目给出粒子运动轨迹一点位置后，找到两点速度方向.此情况下，可通过角平分线交点方式，确定圆心，明确轨道半径与线速度关系，圆心角与已知角关系，通过三角函数关系也能够解答磁偏转问题.

高中生物理知识学习过程中，电磁偏转问题一直是重点物理内容，在学习过程中学生容易将知识混淆.对此，在教学过程中针对电磁偏转问题还需深度分析，对知识点进行总结归纳，从而让学生顺利掌握电磁偏转问题知识，有效解答问题的同时，为学生顺利学习物理知识奠定坚实的基础.