数形结合思想在高中数学解题中的应用
张跃龙
(甘肃省西和县第二中学 742100)
数学主要是将实际生活中的事物通过相应的逻辑关系以及运算关系,在人脑中进行反映,并通过大脑的抽象处理与加工获得的结果.高中生在对数学概念进行学习时,可将抽象知识转变成形象知识,并在解题中,运用大脑对数学试题的含义进行理解.同时,高中生熟练掌握数形结合的数学方法,不仅可以使高中生的解题效率得到有效提高,而且还能使高中生灵活地运用相关数学方法,使高中生实现高效学习.因此,高中生在数学解题时,需注重数形结合思想的运用,以此使学生将相应的数学题目转变为数学图形,从而使学生习题理解力得到提高的同时,实现解题效率的提高.
一、基于数形结合思想的数轴类解题
数轴属于数形结合展现的一种主要方法,通过数轴可构建实数和数轴上各点的对应关系,通过数轴上的“形”实现“数”的融合,以实现解题思路的有效拓展,并迅速地解决相关数学问题,从而使数学知识更具生命力,并实现学生自身的思维视野拓展.
例1 假设集合A={x∣x∈Z,且-10≤x≤-1},B={x∣x∈Z,且∣x∣≤5},那么,A∪B当中的元素个数是( ).
A.11 B.10 C.16 D.15

图1
解析图示法作为集合类试题较为常见的一种表示方法,在对相关抽象问题进行解决的时候,通常能实现形象与直观的目的.对于本题的求解,其主要指集合当中的元素个数,通过数轴的运用,能够有效诠释出集合A与B当中的元素,并把代数问题转变为集合问题实施解决,即根据图1可知,A∪B中共包含了16个整数点.
二、基于数形结合思想的三角类问题解题
对于数形结合而言,其本质内涵就是把数据和图形相结合,以获得相对直观、形象的解题思路.在对三角类的相关问题进行解决时,与相对僵化且常见的代数分析法,通过数形结合的运用,更容易挖掘出其中的几何背景,并对问题的根本进行深入分析,以单位圆呈现的直观性,有效缩短数学问题解决花费的时间.


图2
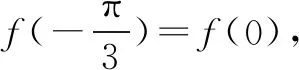
三、基于数形结合思想的不等式类问题解题
高中数学的教学中,学生在对代数式或者方程式的问题进行解答时,通常习惯性地从代数方向实施解答,这种状况下,学生解题就会被“数”所束缚,并影响到问题的高效解决.而通过数形结合的运用,可将代数与方程等问题转变成几何问题,这不仅有利于学生具备的几何直观发展,而且还能使学生顺利解决相关方程或代数问题.


图3

四、基于数形结合思想的函数类问题解题
以图象的形式对函数的相关性质进行研究通常是极其常见的一种方法.在对方程与不等式等相关问题进行解决时,主要是在“数”上进行构“形”,其不仅有利于对题意进行理解,探究相应的解题思路,而且还能体验到解题的结果,从而使函数的抽象化问题得到完美解决,并使学生对函数概念及性质实现高效认识,以此对函数的未知性质进行挖掘,从而使学生的解题思路更加灵活化.
例4 已知log2(-x) 图4 解析本试题将代数作为出发点,就很容易出现思维卡壳,此时,则可融入学生相对熟悉与常用的数形结合,对问题难度进行瓦解,实现解题思路的简化.如图4所示,在解题的时候,可先作出函数y=log2(-x)与函数y=x+1的图象,由题意log2(-x) 在高中数学教学中,在对方程个数进行求解的时候,是最适合使用数形结合思想的.通常情况,在具体的方程个数求解教学中,教师可指导学生结合函数,并将其图形绘制出来.当绘制完成之后,题目也随之解决. 例5 方程ax-x-a=0,已知a的取值范围是(1,+),方程有几个解? 图5 分析如果学生从正面对其进行求解,存在极大的难度,不仅仅浪费了大量的时间,还会导致学生在求解的过程中,出现多种错误.在这种情况下,教师可指导学生将方程转化为两个函数y=ax和y=x+a,借助图5的形式,将函数之间的关系直观、形象地描绘出来,从而根据两个函数图象的交点即可确定几个解,进而帮助学生对其进行解决.如此一来,学生无需花费大量的时间和精力,在极短的时间内,即可对其进行有效的解答.同时,也在很大程度上避免了错误的发生率. 综上所述,数形结合在高中数学解题中具有广泛的应用,以数助形更能够帮助学生找出其中的数学规律和答案,降低学生思考的难度,实现学生解题的有效性.高中数学教师在教学中,应该将数形结合思想渗透到各种数学问题的分析和解决中,让学生能够灵活地进行数与形的转化,帮助学生掌握数学思想的要点及应用范围,提高学生灵活解题的能力和数学思想应用能力,实现学生核心素养的培养.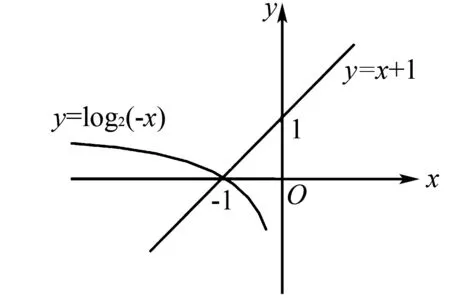
五、基于数形结合思想的方程问题解题


