通过“一题多解”提升学生的高阶思维能力

吕俊君

(九江市同文中学，江西 九江 332000)

1 核心素养与高阶思维

普通高中物理课程标准中提出学生通过物理学科的学习能够具备“科学思维”核心素养.“科学思维”主要包括模型建构、科学推理、科学论证、质疑创新等要素.[1]主要表现在基于原始问题提炼主要因素建构物理模型，能够对物理问题分析推理与论证，在客观事实的基础上对不同观点进行评价与质疑，进而提出创造性的见解.

思维的形成与提升是教育研究中最复杂的内容之一.美国教育家布鲁姆提出教育目标分类包括记忆、理解、应用、分析、评价、创造.达成记忆、理解、应用目标所需的认知能力较低，表现为低阶思维；而分析、评价、创造目标需要更高层次的认知能力，表现为高阶思维.低阶思维是高阶思维的基础，高阶思维是低阶思维进入深度学习区后表现出的具有更高水平的思维过程和成果.[2]2001版布鲁姆教育目标分类情况如表1所示.[3]

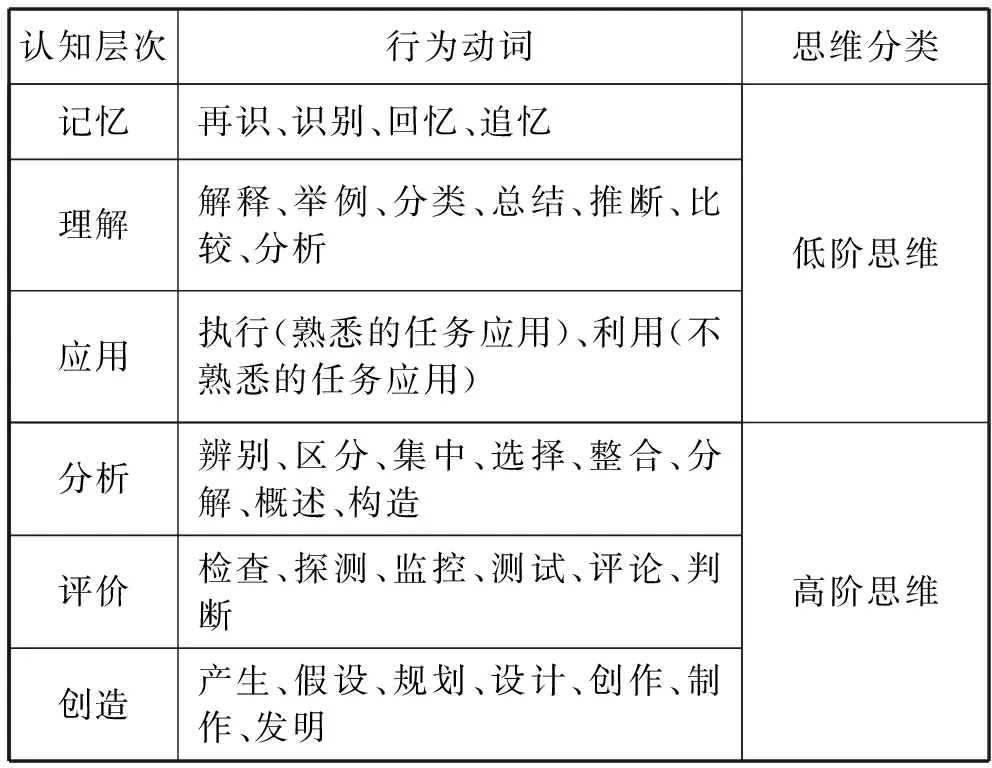
表1 2001版布鲁姆教育目标分类情况

不难看出，“科学思维”核心素养是高阶思维的反映.培养学生的高阶思维能力就必然需要高阶的学习方式，可以通过构建自由开放的思维课堂，鼓励学生点评质疑，提出自己的创造性观点等方式促成高阶思维的训练.

2 “一题多解”与高阶思维

在物理教学中，“一题多解”是常常用到的教学手段.不同方法不仅是解题技巧的差别，更是思维方式的差异.例如物体做匀减速直线运动减速到零求位移这一问题，可以按照匀减速直线运动规律求解；也可以将物体看作反向的匀加速直线运动；还可以应用v-t图像.这些方法对应着正向思维、逆向思维、图像信息等不同的思维方式，教师在教学中如果能够从思维方式切入，引导学生对方法的合理性进行判断、对方法的便捷性进行评论、对方法的普适性进行反思，甚至创造新的方法，将对高阶思维能力的提升起到积极的作用.

3 案例

下面以一道调研题的“一题多解”为案例，探讨高阶思维能力通过“一题多解”的提升.

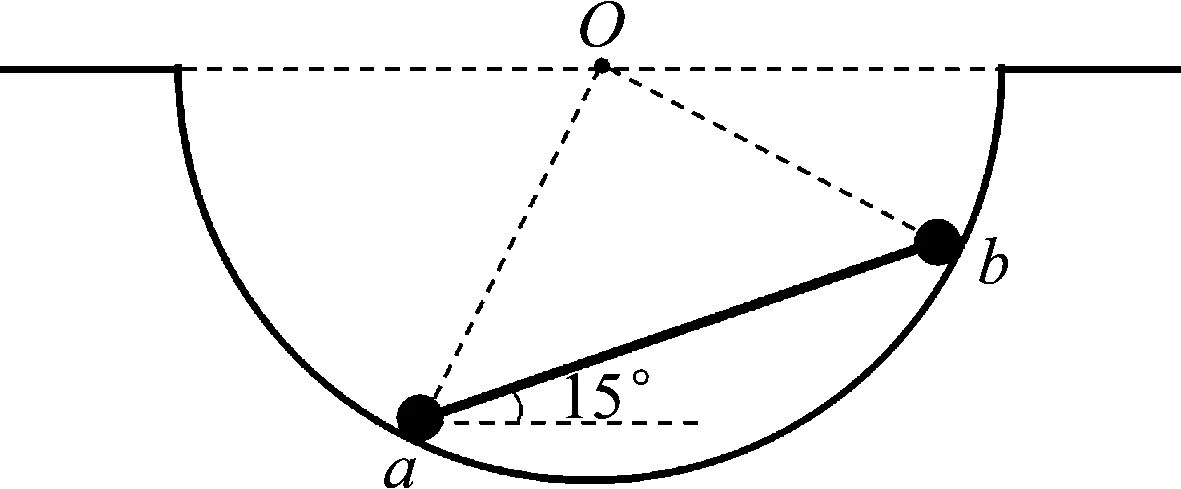
图1 原题图

(1) A同学.A同学采用常规的正交分解法求解.对小球隔离分析，作出受力分析图，沿水平方向和竖直方向建立坐标系，将支持力N1、N2与细杆弹力F分解至坐标轴，如图2所示.列出a、b两物体的平衡方程：

图2 正交分解

N1sin30°=Fcos15°.

(1)

N1cos30°=Fsin15°+G1.

(2)

N2cos30°=Fcos15°.

(3)

N2sin30°+Fsin15°=G2.

(4)

(2) B同学.B同学对A同学的解法表示肯定，但B认为：“A的解法过于繁琐，原因在于将力分解至水平方向与竖直方向，既要分解F，也要分解N1与N2，而15°的正弦余弦值也不常规，计算量相当庞大.”在A同学的基础上，B同学提出了改进方法如下.

沿球所受碗的支持力方向与垂直碗的支持力方向建立直角坐标系，将重力G1、G2与细杆弹力F分解至坐标轴，如图3所示.列出a、b两物体的平衡方程

G1cos60°=Fcos45°.

(5)

G2cos30°=Fcos45°.

(6)

图3 正交分解(改进后)

(3) C同学.C同学认为：“A同学的思路虽然常规，但计算量庞大；B同学解法虽然便捷，但这种建立坐标系的思维难以在考场上想到.考虑到本题属于三力平衡问题，采用三角形定则求解是本类问题的普适性方法.”于是C同学提出解法如下.

依据三角形定则将碗对a球的支持力N1和细杆对球的弹力F合成，合力与重力G1等大反向，b球同理.如图4所示.

对a球分析，由正弦定理得

(7)

同理对b球分析得

(8)

图4 三角形定则(结合正弦定理)

(4) D同学.D同学认为:“C同学的思路固然清晰,但解题所需的数学工具为正弦定理,必须对正弦定理的使用很熟练,而且要寻找题中的各种角度.在C同学的基础上,不需要正弦定理,借助初中学习的三角形相似就可以求出.”随后,D同学展示解法如下:

过圆心作竖直辅助线交细杆于C点,过a球作辅助线垂直OC交于E点;过b球作辅助线垂直OC并交于D点,如图5所示.

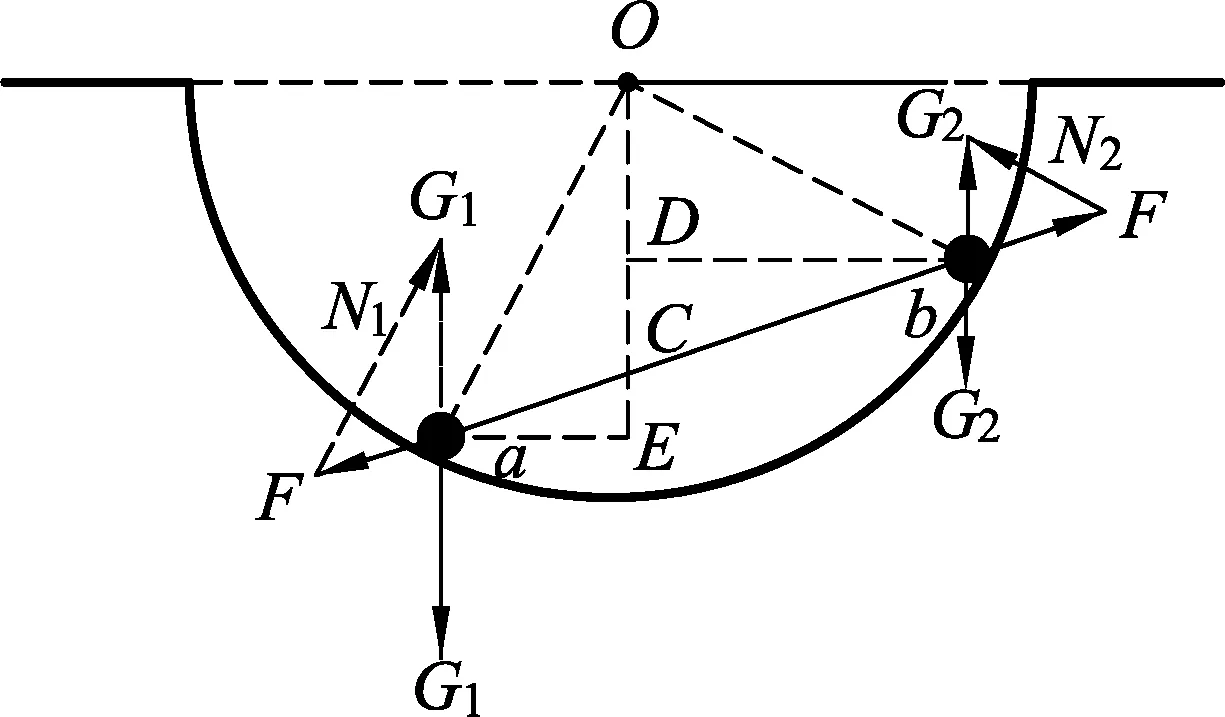
图5 三角形定则(结合三角形相似)

对a球分析可得,力三角形aG1F与几何三角形OaC相似,有

(9)

同理对b球分析可得

(10)

根据△aCE与△bCD相似可知

(11)

(5) E同学.E同学提出了完全不同的观点:“本题可以运用力矩平衡的方法求解,选择两个球与轻质细杆整体为研究对象,碗对两球的支持力均指向球心,如果选择球心为转轴,则支持力的力矩为零,只要计算重力的力矩就可以解出答案,非常快捷.E同学解法如下.

对a、b与细杆整体分析,以O点为转轴,支持力N1与N2不产生力矩.G1产生逆时针转动效果的力矩,力臂为OD,G2产生顺时针转动效果的力矩,力臂为OE,如图6所示.

图6 力矩平衡

根据几何关系得

OD=Rcos60°.

(12)

OE=Rcos30°.

(13)

根据力矩平衡条件可得

G1·OD=G2·OE.

(14)

(6) F同学(参加全国中学生物理竞赛).F同学是全国中学生物理竞赛培训班的一员,通过竞赛课的学习,他接触了理论力学相关知识,并且意识到该系统受到理想约束.受到理想约束的力学体系平衡的充要条件是此力学体系的诸主动力在任意虚位移中所作元功之和等于零.这个关系是1717年伯努利首先发现的,叫做虚功原理,也叫虚位移原理.[4]于是,他提出了自己的解法,受到了同学们的一致好评.

设ab整个系统以O点为中心旋转了一个虚位移角δθ,如图7所示.在这一过程中主动力G1与G2做虚功.由几何关系可知a球升高了虚位移:

图7 虚功原理

δh1=Rcos30°-Rcos(30°+δθ)=R(cos30°-cos30°cosδθ+sin30°sinδθ).由于δθ极小,在数学上cosδθ=1,sinδθ=δθ,故

(15)

同理b球降低了虚位移

δh2=Rcos(60°-δθ)-Rcos60°=

R(cos60°cosδθ+sin60°sinδθ-cos60°)=

(16)

根据虚功原理,

δW=-G1δh1+G2δh2=0.

(17)

4 评价与结语

4.1 评价

A同学采用常规的正交分解法,将力分解至水平和竖直方向,列出4个方程.B同学敏锐地发现A同学解法繁琐的核心原因在于坐标轴的选取不合适,于是在其基础上改变了坐标轴的选择,只需列出两个方程就求出答案.从思维来看,B同学能够意识到A同学坐标轴选择的不够合理,说明具备了一定的判断与评价能力;能够根据自己的判断得出更加简便的方法,说明具备了一定的分析能力.就本题而言,B同学展现出更高层次的思维.

C同学提出用三角形定则求解三力平衡问题,说明他脑海中存在一个意识:“正交分解法虽然普适性强,但更多用于四力

及更多力的问题,对于三力平衡,三角形定则更加高效.”这表明C同学已经对两种方法进行了区别和分类,能够准确的筛选出解决此类问题的高效方法.在数学工具选择上,应用了正弦定理求解,体现出跨学科的思维能力.D同学和C同学的区别在于数学处理方式的差异,将问题的信息集中在受力分析图上,用平面几何的思维解决物理问题.这两位同学均展现出了区分、筛选、分析等能力,在思维层面上高于A、B两位同学.

E同学解法的区别不仅是应用了力矩平衡,而且是研究对象选择的差异.前面4位同学的做法都没有脱离隔离法这一框架,而E同学选择对整体分析,体现出整体的研究思想,说明他能够根据具体的问题选择合适的对象.E同学解法的另一亮点在于转轴的选择上,应用力矩如果转轴选择不合适,只会适得其反,该同学选择球心为转轴,消去了支持力的力矩,大大减少了计算量.F同学通过竞赛课获得了更为宽阔的思维,突破了牛顿力学的束缚,采用分析力学的思维求解静力学问题.虽然这种解法对高中生不做要求,但对开阔学生思维依然有积极作用.总体而言,这两位同学均体现出了辨别、区分、选择、整合、判断、创造等能力,体现出高于前面四位同学的思维能力.

4.2 结语

本题的研究不局限于此,教师也可以引导学生对问题进行拓展,让学生改变题中的相关条件创造新的问题.例如: (1)本题中碗对球的弹力之比为多少? (2) 如果将两球质量改为相等,从图中所示位置静止释放,则两球的最大速率为多少?(设半球形半径为R,重力加速度为g).可以将习题改编作为一项课后作业,进一步强化思维能力的提升.总之,高阶思维的提升是物理教学中非常重要的一项课题,只要教师勤于思考、敢于尝试,一定能获取更多的经验与成功.