基于光谱数据的南疆农田土壤有机碳含量估算模型研究
张 丽 郝梦洁 鲁新新 郭又波 阿迪力·亚森 蒋青松
(塔里木大学信息工程学院,新疆 阿拉尔 843300)
随着全球气候变化研究的深入,围绕全球气候变化中土壤有机碳库的研究受到普遍关注[1]。土壤有机碳(soil organic carbon,SOC),是指土壤中存在各种形式和状态的碳化合物[2],包括动物、植物和微生物的遗骸以及降解和合成的产物。这是土壤中天然有机物的精细非生物形式的通用名称。土壤有机碳作为土壤最重要的组成成分,是土壤质量的核心,是准确评价土壤肥力的重要依据,也是全球碳循环和气候变化研究的一个重要内容,地球表面最大的碳库是陆地土壤,陆地上的有机碳储量约为1 550 Pg[3]。农田土壤具有比较高的固碳潜力,并且可以有效地减少大气中二氧化碳(CO2)的浓度,其中有机碳的含量是判断该土壤质量极其重要的指标之一,有机碳含量的减少不仅会导致农田生态的退化,而且还会降低农田的可持续利用性[4]。由于土地利用的变化,自19世纪以来,大气中二氧化碳的大部分增加是由于将自然土壤转化为永久性农业用地而导致的。农田上的土壤碳沉积直接影响大气中碳沉积的源汇效应。在全球陆地生态系统的碳库中,农业土壤碳存储在很大程度上被人类破坏,并使得其可以进行短期的人为调控[5]。荒漠地区的发展和农业用地的耕作,导致养分的流失和土壤结构的破坏以及土壤中二氧化碳的降解。农业用地是大气中温室气体积累的主要因素[6]。
高光谱技术具有高分辨率、多波段和图谱合一的特点,由于其独特的光谱特征而被广泛用于农业、工业和医学领域,可以说是未来遥感技术的最重要技术之一[7]。数十年来发展起来的高光谱技术,在研究土壤有机质方面做了大量的工作,为后续研究者提供了良好的借鉴。徐彬彬等[8]比较有机质去除前后土壤光谱反射率曲线的变化,发现可见光是监测土壤有机质含量的重要波长范围;于雷等[9]运用偏最小二乘回归建立了土壤有机质含量的估算模型,CARS-SPAPLSR混合模型不仅简单,且预测效果较好,该模型可以作为评估该地区土壤有机质的重要方法,对未来土壤近地传感器设备的发展具有明确的方向性作用;郭斗斗等[10]利用25种光谱预处理方法,结合3种建模方法来构建不同的潮土有机质高光谱预测模型。偏最小二乘回归模型结合最大值标准化预处理所建模型精度高、可靠性强,且建模过程数据运算更为简便,是筛选出的最佳潮土有机质高光谱预测模型。新型的高光谱遥感技术在很大程度上弥补了传统监测的空白,并且由于其动态、快速、高效和宏观经济的优势,它逐渐取代了传统的监测方法,成为了区域监测土地资源探测新方法[11];丁建军等[12]详细论证建模过程中建模组样本数与验证组样本数的数量关系,分析得出基于PLSR的土壤有机碳预测模型最优条件;李硕等[13]使用主成分回归,偏负平方回归和传播神经网络对基于可见-近红外光谱数据的土壤氮进行预测,并比较三种建模方法以选择最佳模型;卢艳丽等[14]对基于近红外数据利用逐步回归分析和主成分回归分析建立了东北黑土有机碳回归预测模型;Gimsauh等[15]研究发现土壤有机质含量与红光波段的反射率具有较高的相关性。这些研究表明可以使用高光谱对有机碳进行监测,但所有研究都是线性模型,不能很好地解决非线性问题。因此,在今后的研究中尝试用非线性模型对土壤有机碳的预测是十分必要的。
南疆位于我国西北部,天山以南,地处于干旱、半干旱荒漠地区,腐殖质的合成和有机碳的分解受到土壤水分的强烈影响[16]。南疆广阔的土地资源是我国重要的农业地区,4.27%的土地资源承载着95%以上的人口,随着人口的增长,现有土地资源无法满足经济社会发展的需要,对进一步开发和利用土壤资源提出了新的要求[11]。如何合理开发并利用现有的土壤资源对于社会经济可持续发展尤为重要。土壤肥力是合理开发利用土壤资源的重要参考依据,而土壤有机碳是评估土壤肥力的主要指标。因此,如何快速、有效地监测土壤中有机碳的含量,为合理开发和利用土壤资源提供科学依据已成为南疆农业经济的重要需求点[17-18]。传统测定有机碳的方法虽然具有较高的准确性,但会花费较多的人力、物力和财力,难以快速的监测到土壤中有机碳的动态变化趋势,其测定结果通常具有滞后性,无法满足实际应用的需求。随着3S技术的快速发展,其作为一种重要的监测工具,在土壤信息中的应用也日益广泛[19]。作为遥感技术(RS)重要组成部分的高光谱技术以其快速、有效、经济和环保等属性被广泛应用于有机碳含量的估算,为有机碳的定量研究提供了新方法[20-21]。Dematte等[22]、徐彬彬[23]、彭杰等[24-25]甚至发现无论在全波段还是在紫外、可见光和近红外波段去除土壤有机质均可以提高土壤的反射率。研究表明:在600 nm附近的波段处,有机质与土壤光谱之间的弓曲呈现负相关关系[26];土壤有机质含量与反射率之间具有非线性和显著负相关性[27]。当前对于土壤有机质的定量估算在空间尺度上主要限定于局域性研究,对于类似全球性的大尺度、全局性的研究工作,基于采样的复杂性、时空的变异性、建模方法的稳健性和模型精度的局限性等因素,致使相关报道鲜见。在现有的文献中,有关南疆土壤有机碳定量估算的研究报道比较少见,且已有研究工作在估算精度方面有待进一步提高。鉴于以上分析,本文以新疆维吾尔自治区南疆地区的阿瓦提县、温宿县、和田市、新和县等四个地区的农田土壤为研究对象,运用Unscrambler 10.5对光谱数据做多项式平滑、归一化、线性基线校正、标准正态变量变化、多项式平滑+归一化等作变换处理,据此对光谱数据做相关性,并运用全波段数据利用偏最小二乘法以及主成分回归法来构建土壤有机碳的估算模型,以期从5种预处理方法中,筛选出建模精度最佳的预处理方法,从而通过比较获取较优的有机碳预测模型,并将其应用于南疆农田土壤有机碳含量的定量评估与分析中。相关研究工作为简便、快速、有效地监测土壤有机碳的含量提供了重要依据与技术支持。
1 材料与方法
1.1 样本采集
在新疆维吾尔自治区南疆地区阿瓦提县(北纬39°31′~40°50′、东经 79°45′~81°05′)、温宿县(北纬 40°52′~42°15′、东经 79°28′~81°30′)、和田市(东经79°50′20″~79°56′40″、北纬36°59′50″~37°14′23″)、新和县(东经80°55′~82°43′、北纬40°45′~41°45′)进行样本采集,采样区域分布图如图1所示。
采用网格采样法在研究区域0~20 cm土层采集261份土样,样点的间隔大约100 m,以起始点为样点中心,沿着东、西、南、北四个方位进行土样的采集,每个方位的样点几乎在同一条水平线上,每个土样的质量大约为2 kg[28]。将采集的土样带回室内,在实验室风干,然后将一部分土样经过细磨,过孔径2 mm筛选处理,用于光谱测试;另一部分土样细磨过孔径2.5 mm筛选处理,用于理化性质分析。处理过的土样均匀的混合后,分别按照其名称装在自封袋中[17]。经过测试,供试土样的有机质统计数据如表1所示。
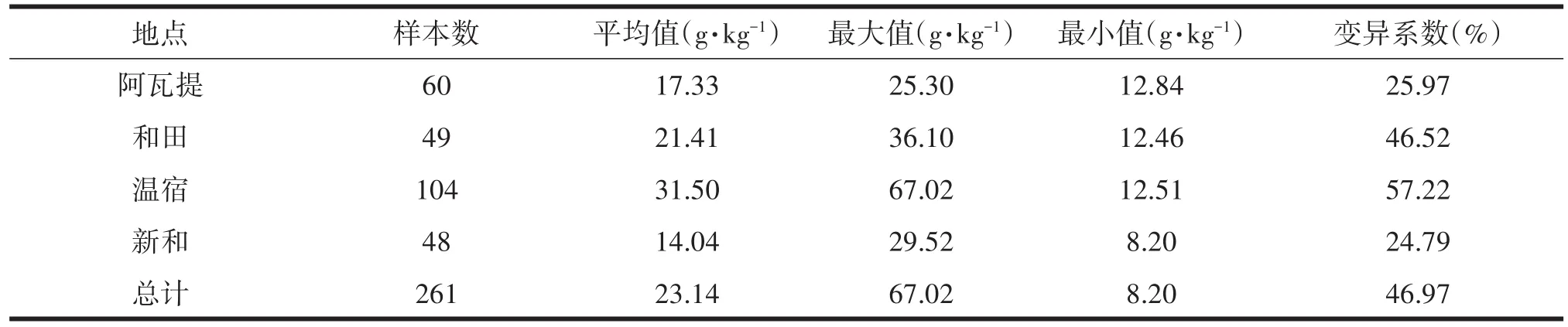
表1 供试土样有机质数据统计
通过分析表1数据可知,四个样区土样的有机质含量有着明显的差异,其中,温宿地区土样的有机质平均含量最高,新和地区有机质的平均含量最低;从有机质含量的变异系数来看,也是来于温宿地区土样的有机质变异系数最大,而来于新和地区有机质的变异系数最小。统计数据与实际情况吻合度较高。
1.2 光谱测定与数据处理
使用美国ASD公司的Field Spec Pro FR光谱仪采集土壤光谱数据,其波长范围在350~2 500 nm之间,在350~1 000 nm之间光谱采样间隔为1.4 nm,光谱的分辨率为3 nm;1 000~2 500 nm的光谱采样间隔为2 nm,光谱的分辨率为10 nm。光谱仪最终将在1 nm处对数据进行重新采样[29]。光谱的测量在一个可以控制光照条件的暗室内进行,光源为50 W的卤素灯,距土壤样品表面不超过70 cm,天顶角为30°,将土壤样品放在直径10 cm和深2 cm的容器中,刮平表面。采用的探头为25°视场角探头,传感器探头位于土样表面正上方15 cm处。在测试之前,需要进行白板校正。每个土壤样品采集10条光谱曲线,并以算术平均值获得了该土壤样品的实际反射光谱数据[30]。光谱仪器在收集数据时容易受到环境影响,而且收集的数据通常包含很多噪声。此外,光谱仪器还会收集大范围波段的光谱数据。因此,对于模型需要的数据有必要进行异常数据剔除。因此,本文使用The-Unscrambler 10.5对光谱数据分别进行了以下变换处理:多项式平滑、归一化、线性基线校正、标准正态变量变化、多项式平滑+归一化等。
1.3 建模方法
1.3.1 偏最小二乘法
偏最小二乘法不仅是一种基于多因变量与多自变量之间相关关系的回归建模方法,也是一种新型的多元统计分析方法,该方法集成了相关性分析、主成分分析以及多元线性回归技术的特点,能够有效地解决多因变量对多自变量的回归建模以及光谱波段间存在的多共重线性问题[12]。PLSR对样本数量的要求较低,当样本个数小于自变量个数时,PLSR也可以建立回归模型。它与主成分分析法都可以提取数据的特征信息,它有一个“响应”矩阵,且它提取的成分不仅可以很好的概括自变量系统中的信息,还可以很好的解释因变量,因此具有估测功能[31]。
1.3.2 主成分回归法
主成分回归法是回归分析方法的一种,它不但可以解决自变量间存在的多重线性问题[32],在保留原有信息的基础上还有降维的作用。它在1965年被马西提出,其基本步骤如下:第一步:把自变量转变为标准分;第二步:求出标准分的主成分并去除特征根较小的主成分;第三步:对因变量与剩下的主成分做回归;第四步:将回归方程中的主成分换成标准分的线性组合,得到回归方程。
1.4 数据划分与精度评价
将261个样本按比例(2:1)分成建模集和预测集,即174个样本用于建模,87个样本用于模型预测,建模集与预测集有机碳数据见表2。建模方法主要采用基于偏最小二乘法以及主成分回归。评价模型稳定性和预测准确性的指标为R2、RMSE、RPD。其中RPD是量纲指标,其值越大,表明模型的预测能力越强,RPD划分见Saeys[33]。模型的R2越大,RMSE越小,其预测精度就越高越稳定。
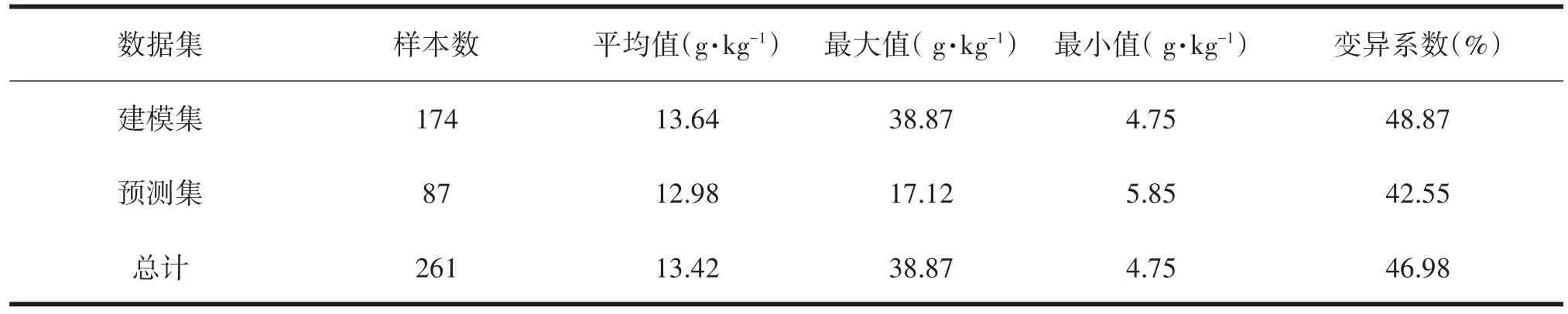
表2 建模集与预测集有机碳数据统计
2 结果分析
2.1 土壤有机碳与高光谱数据的相关性分析
将土壤有机质含量与光谱原始数据以及经过多项式平滑、归一化、线性基线校正、标准正态变量变化、多项式平滑+归一化变换处理后做相关性分析,且做相关系数在0.01水平上的显著性检验,如图2所示。
农田土壤有机碳含量与原始数据、多项式平滑、线性基线校正只有正相关,原始数据与多项式平滑710~962 nm、1 258~1 392 nm、1 686~2 645 nm、3 621~3 999 nm波段的相关性通过0.01水平上的显著性检验(图2a、图2c),且最大正相关系数位于1 686~2 645 nm波段,相关系数达到了0.502;线性基线校正只在1 686~2 645 nm、3 621~3 999 nm波段的相关性通过0.01水平上的显著性检验(图2e),最大正相关系数位于1 686~2 645 nm波段,相关系数达到了0.486;而光谱原始数据经过归一化(图2b)、多项式平滑+归一化(图2d)、标准正态变量变化(图2f)变换后,不仅有正相关,还有负相关,这三种变换形式在1 756~2 041 nm、2 468~2 605 nm波段呈正相关,在1 033~1 210 nm、1 492~1 565 nm波段呈负相关,且在1 756~2041 nm、2 468~2 605 nm、1 033~1 210 nm、1 492~1 565 nm波段的相关性通过0.01水平上的显著性检验(图2b、图2d、图2f),最大正相关系数位于1 756~2 041 nm波段,相关系数达到了0.527,最大负相关系数位于1 033~1 210 nm波段,相关系数达到了-0.410。光谱原始数据经过归一化(图2b)、多项式平滑+归一化(图2d)、标准正态变量变化(图2f)变换后所得到的光谱数值与土壤有机质含量相关系数与多项式平滑、线性基线校正变换后相比均有提高。原始数据、多项式平滑、线性基线校正与有机碳含量相关性的连续性较差,正相关和负相关的规律性较弱。而经过归一化、多项式平滑+归一化、标准正态变量变化处理后,有机碳含量的相关性看起来更简单、更具连续性。
2.2 偏最小二乘法农田土壤有机碳高光谱估算模型
基于PLSR方法的有机碳估算模型中,预处理方法采用多项式平滑、归一化、线性基线校正、标准正态变量变化、多项式平滑+归一化,其中多项式平滑+归一化的模型建模效果相对最好。表3给出无预处理和经预处理多项式平滑、归一化、线性基线校正、标准正态变量变化、多项式平滑+归一化的基于PLSR的有机碳估算结果精度。图3给出基于多项式平滑+归一化处理后的PLSR有机碳含量模型的估算结果散点图。相比其他数据预处理的PLSR估测模型而言,经多项式平滑+归一化的PLSR估算模型的精度更高、预测能力更好。

图2 农田土壤有机碳含量与光谱变换形式的相关性曲线
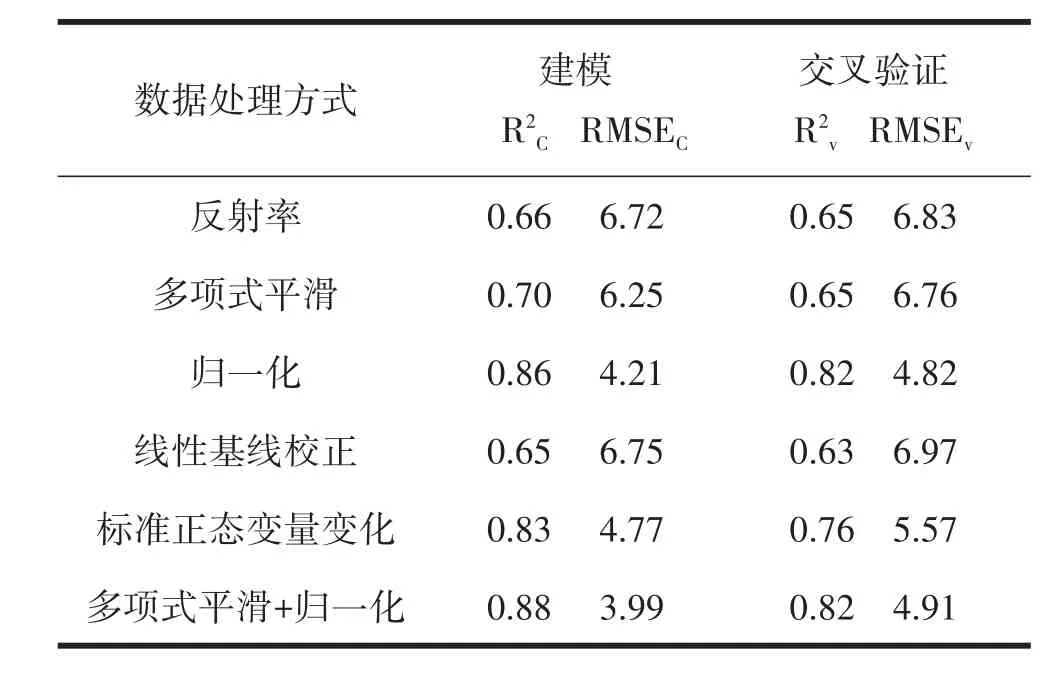
表3 偏最小二乘法不同数据预处理方法的精度对比
从表3中可以看出,就PLSR模型而言,无预处理与5种预处理方法中建模集的R2C均高于交叉验证集的R2V,而RMSEC则均低于对应的RMSEV。在无预处理与5种预处理方法中,基于多项式平滑+归一化处理后的PLSR估测模型的决定系数R2C最高,为0.88;均方根误差RMSEC值最低,为3.99。基于归一化与多项式平滑+归一化处理后的PLSR估测模型的R2v一样,且基于归一化的PLSR估测模型的RMSEv更低。研究表明,在反射率、多项式平滑、归一化、线性基线校正、标准正态变量变化、多项式平滑+归一化这无预处理与5种预处理方法中,经归一化与多项式平滑+归一化处理后的建模精度最高。据此表4给出基于归一化与多项式平滑+归一化处理后的PLSR预测结果精度。

表4 偏最小二乘法方法的归一化与SG平滑+归一化预测精度对比
由表4中可知,基于归一化与多项式平滑+归一化处理后的PLSR估测模型,多项式平滑+归一化处理后的建模精度最高,其R2、RMSE、RPD分别为0.84、3.47 g·kg-1、2.63。为了验证该模型经多项式平滑+归一化后的精度与稳定性,本文用建模之外的87个样本对估算模型进行了验证,验证结果的预测值与实测值的散点图如图3所示。
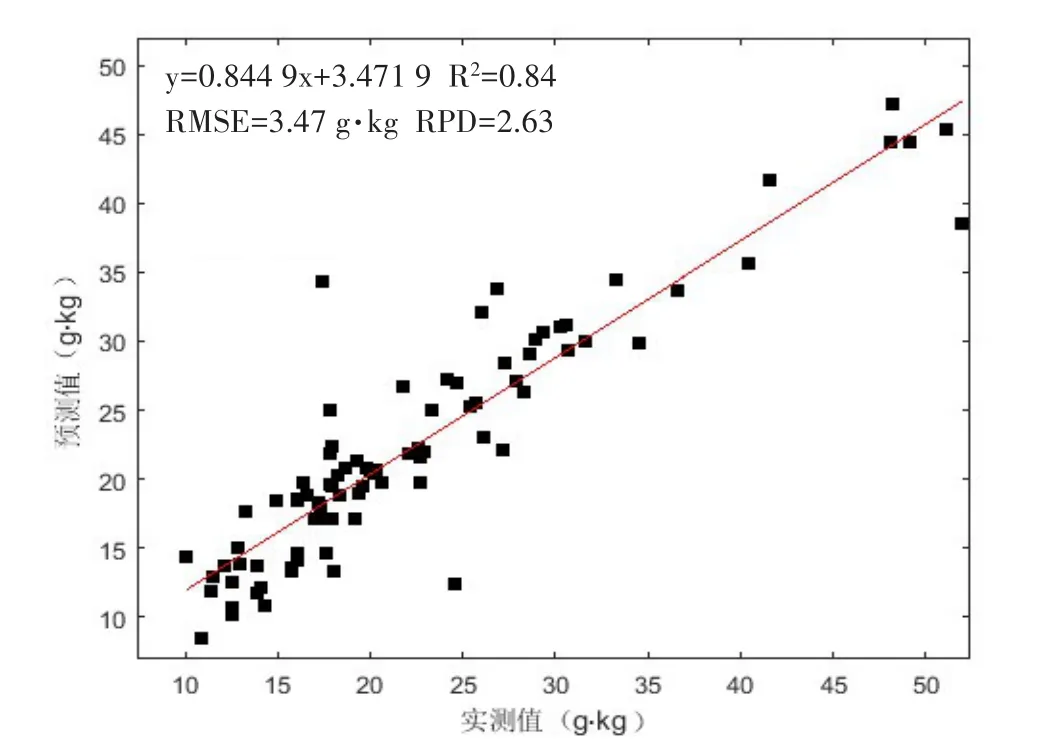
图3 基于多项式平滑+归一化处理的PLSR有机碳含量模型的估算结果散点图
由图3可以看出,87个土壤样本有机碳含量的PLSR模型预测值与实测值之间的R2为0.84,RMSE为3.47 g·kg-1,与PLSR模型在建模集(0.88和3.99)和交叉验证集(0.82和4.91)的数值相差不多,该RMSE甚至比交叉验证集的RMSE更低,说明PLSR模型的稳定性较好,而RPD为2.63,根据Saeys等[33]的评价标准,说明该模型具有较好的预测能力。
2.3 主成分回归农田土壤有机碳高光谱估算模型
基于PCR的有机碳估算模型中,预处理采用多项式平滑、归一化、线性基线校正、标准正态变量变化、多项式平滑+归一化,其中经过标准正态变量变化预处理的模型建模效果相对最好。表5给出无预处理和经预处理(多项式平滑、归一化、线性基线校正、标准正态变量变化、多项式平滑+归一化)后,采用PCR建模得到的结果精度。图4给出基于标准正态变化变量处理后的PCR模型的估算结果散点图。相比其他数据预处理的PCR估测模型而言,经标准正态变量变化处理后的PCR估算模型的精度更高、预测能力更好。
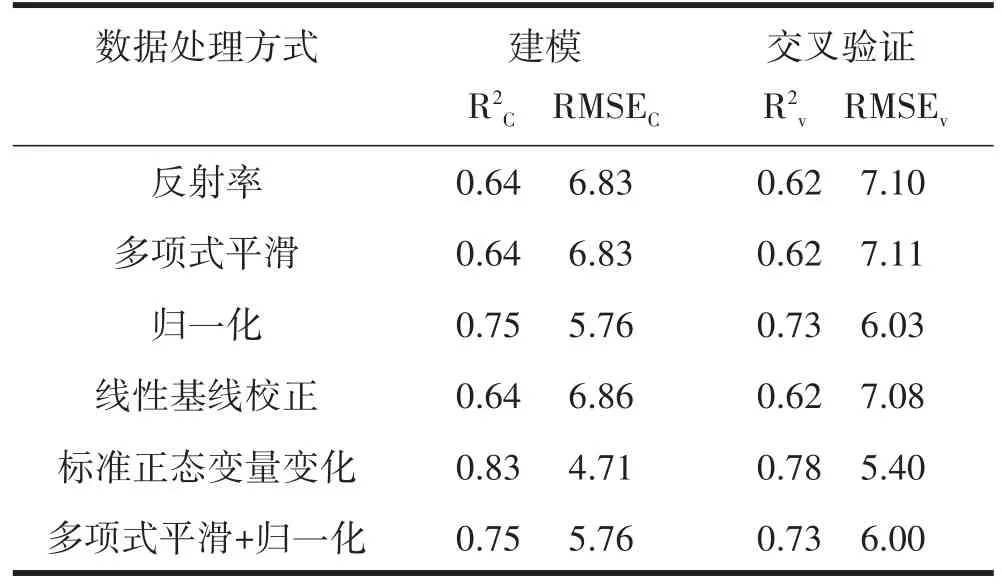
表5 主成分回归方法不同数据预处理方法的精度对比
从表5中可以看出,就PCR模型而言,无预处理与5种预处理方法中建模集的R2C均高于交叉验证集的R2V,而RMSEC则均低于对应的RMSEV。在5种预处理方法中,基于标准正态变量变化处理的PCR估测模型的决定系数R2C值最高,为0.83;均方根误差RMSEC值最低,为4.71。研究表明,针对无预处理与5种预处理方法(多项式平滑、归一化、线性基线校正、标准正态变量变化、多项式平滑+归一化)而言,标准正态变量变化处理后的建模精度最高。
由表5中可知,在PCR建模所涉及的无预处理与5种预处理方法中,标准正态变量变化的建模精度最高,其R2、RMSE分别为0.83、4.71 g·kg-1,为了验证该模型经标准正态变量变化处理后的精度与稳定性,本文用建模之外的87个样本对估算模型(PCR)进行了验证。验证结果的预测值与实测值的散点图如图4所示。
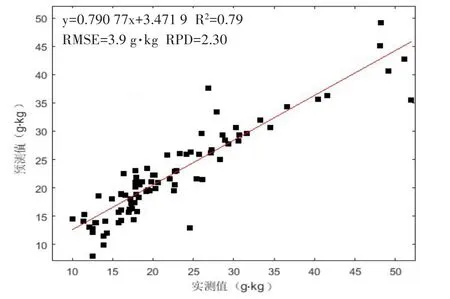
图4 基于标准正态变量变化处理的PCR有机碳含量模型的估算结果散点图
由图4可以看出,87个土壤样本有机碳含量的PCR模型预测值与实测值之间的R2为0.79,RMSE为3.9 g·kg-1,与PCR模型在建模集(0.83和4.71)和交叉验证集(0.78和5.40)的数值相差不多,该RMSE甚至比交叉验证集的RMSE更低,说明PCR模型的稳定性较好,而RPD为2.30,根据Saeys等[33]的评价标准,说明该模型具有较好的预测能力。
2.4 有机碳含量高光谱估算模型结果对比分析
表6给出PLSR与PCR方法在最优预处理下的模型估算对比结果。从表6可看出,就有机碳含量的模型估算结果而言,数据在经预处理后,PLSR已经明显优于PCR。

表6 偏最小二乘法与主成分回归法的有机碳高光谱估算模型结果对比
此外,在经预处理后,无论是PLSR还是PCR,模型精度较之预处理前都有显著提升。研究结果表明:针对同样的数据预处理方式,就PLSR与PCR方法比较而言,前者RMSEv的值更小,而R2v的值更大,同时RPD的值更高。因此,PLSR比PCR方法的建模精度更高、预测能力更好。由此可见,PLSR较PCR更适用于土壤有机碳含量的估算。
3 结论
土壤有机碳的含量作为评价土壤肥力的重要依据,探索土壤有机碳快速、有效的监测方法对土壤资源的合理开发和利用有重要的意义。本文对采集新疆维吾尔自治区阿瓦提、温宿、和田、新和的261个农田土壤样本,运用5种预处理方法,并结合偏最小二乘法以及主成分回归法,来构建阿瓦提、温宿、和田、新和农田土壤有机碳的估算模型。
研究结果表明:5种预处理方法中,基于多项式平滑+归一化处理的偏最小二乘模型精度最高,其R2为0.84,RMSE为3.47 g·kg-1,RPD为 2.63;基于标准正态变量变化处理的主成分回归模型精度也较高,其R2为0.79,RMSE为3.9 g·kg-1,RPD为2.30;根据Saeys等[33]的评价标准,这两种模型都具有较好的预测能力,但前者因其R2更大,RMSE更小,同时RPD也更高,从而具有更好的预测效果。因此,针对相同的数据处理方式而言,PLSR较PCR方法更适用于土壤有机碳含量的估算。
尽管本文仅运用了5种数据预处理方法(多项式平滑、归一化、线性基线校正、标准正态变量变化、多项式平滑+归一)及两种非线性模型偏最小二乘法和主成分回归法,所得模型结果均比较理想,用于预测的效果较好。但因土壤有机碳含量的估算问题,基于问题本身的复杂性和模型预测精度的不确定性,随着科技的进步和研究工作的深入,势必会产生更多更优的预测模型,期待更多相关领域的研究成果,用以丰富其理论知识和实践应用。

