热压工艺对涤纶湿法非织造材料断裂强力的影响及优化控制
郑 帏 刘倩男 庄旭品 汪晓银*
(1天津工业大学数学科学学院,天津 300387)
(2天津工业大学纺织科学与工程学院,天津 300387)
水污染以及淡水资源匮乏都是当今全球面临的主要问题之一[1]。膜分离技术在水处理方面具有高效率、低能耗、自动化程度高的优势,是缓解淡水资源短缺的有效途径[2-3]。
目前,微滤、超滤、纳滤以及反渗透技术在我国水净化、水处理领域得到了大规模应用,相应分离膜的研发也得到了快速发展[4-7]。纳滤膜和反渗透膜等分离膜被广泛应用于海水淡化领域,其结构通常包括一层极薄的皮质层、聚合物多孔支撑层和织物支撑层。皮层通常为聚酰胺薄膜脱盐层,其功能是保留溶质,多孔支撑层为膜提供了一定的强度,通常是由聚砜或聚醚砜等聚合物在相分离过程中产生的,底层的织物层可以是机织物、针织物或非织造布,主要为膜提供高强度的机械支撑[8-9]。研究发现,当膜的机械强度不足时,膜在运行过程中的变形对膜的结构和性能有显著影响[10-11]。理想的分离膜支撑体应具有均匀光滑的表面、合适的孔隙结构和优良的力学性能,这是评价反渗透膜支撑体性能优劣的重要指标[10,12-14]。
湿法非织造技术所制备的非织造布表面平整均匀,力学性能优异,具有各向同性,被广泛应用于分离膜支撑体[15-16]。在湿法成网过程中,通常将低熔点纤维与高熔点纤维混合分散在水介质中形成纤维悬浮液并输送到成网机构,纤维在湿态下成网并烘干。湿法技术突破了传统的纺织原理,该技术无需对纤维原料进行反复加工,大大降低了能耗,节省了人力物力。然而,湿法技术所形成的非织造布纤维间的粘结强度较低,纤维网通常是疏松的。因此,需要对湿法非织造布进行物理或化学处理,以克服这些缺点,提高其力学性能[17]。热压粘合工艺是提高湿法非织造布机械性能的一种有效方法。通过热压辊或热压板对非织造布进行加热加压,低熔点纤维在压力和温度的联合作用下逐渐软化熔融,在纤维间流动和扩散,冷却后,纤维被粘接,从而提升了纤维间的结合力,非织造布的机械性能也会随之提升[18-19]。
非织造材料的力学性能不仅受到湿法成网均匀性的影响,还受到热压温度、时间和压力等不同热压参数的影响。上述三种工艺参数的配合调整对非织造布材料的结构和力学性能有显著影响,如果仅采用全试验设计,显然加重了实验难度。因此本文选择正交试验设计进行实验,简化实验过程。
1 涤纶湿法非织造材料断裂强力的热压工艺影响实验
1.1 实验试剂与仪器
实验中非织造材料制备所用纤维:常规涤纶纤维(PET-260),0.5 D*3 mm,熔点260℃,宝泓新材料有限公司(广州,中国);低熔点涤纶纤维(PET UDY),1.6 D*5 mm,熔点180℃,东丽(中国)投资有限公司;聚氧乙烯(PEO),500 kDa,阿拉丁试剂有限公司(上海,中国)。
实验中非织造材料制备所用仪器:纤维标准解离器,AT-XW,山东安尼麦特仪器(中国);湿法成型器,山东安尼麦特仪器(中国);平板热压机,PCH-600DG,天津恒创科技(中国);磁力搅拌器,78-1,山东鲁华电热仪器(中国);万能强力测试仪,YG028,温州方圆仪器(中国);数字测厚仪,YG141LA,莱州市电子仪器(中国)。
1.2 涤纶湿法非织造材料制备
涤纶湿法非织造材料通过现代湿法造纸工艺和热压技术制备得到。首先,在纤维标准解离器的槽桶内中加入2 250 mL水、2 mL 0.5% PEO分散剂以及6:4比例的1.507 g PET-260纤维和1.005 g PET UDY纤维,启动解离器分散纤维以形成纤维悬浮液。然后,将悬浮液倒入纸页成型器的容器中以排干绝大部分水形成湿的纤维网,将湿纤网在100°C下干燥10 min形成涤纶湿法非织造材料。最后,通过平板热压机对涤纶湿法非织造材料进行热压粘合从而获得涤纶湿法非织造薄膜。
1.3 热压参数设计
1.3.1 控制因素
本文通过湿法成网-热压工艺制备涤纶湿法非织造材料,探究热压工艺参数对非织造材料性能的影响。将热压工艺参数(热压温度、热压压力以及热压时间)作为控制因素,探究热压工艺参数对非织造材料的断裂强力的影响及优化热压工艺条件。经过多次的反复实验,确定了热压工艺参数的范围。其中,热压温度:205℃,210℃,215℃;热压压力15 Pa,16 Pa,17 Pa;热压时间20 s,30 s,40 s。
1.3.2 正交试验表
根据控制因素的取值,设计了热压温度、热压压力以及热压时间的三因素三水平L9(34)的正交试验。正交试验设计的具体情况见表1。
1.3.3 实验数据
依据正交试验表制备涤纶非织造材料,测量其断裂强力。为了使数据具有准确性和可靠性,同时研究交互作用的效应,需在同一组控制因素下重复三次实验,依次将9次正交试验的热压温度、热压压力、热压时间、断裂强力的实验数据列出,见表1。

表1 正交试验的实验数据
1.4 涤纶湿法非织造材料的形貌表征
涤纶湿法非织造材料的断裂强力采用万能强力测试仪进行拉伸实验。图1为涤纶湿法非制造材料热压前后的扫描电镜图,其中a,b,c,d分别表示涤纶湿法非织造材料热压前表面、热压前横截面、热压后表面、热压后横截面。给出这些电镜图目的是观察热压之前和之后的非织造材料表面和横截面的变化情况。如图1(a,b),在热压之前纤维相互缠绕,并且排列松散无序,涤纶湿法非织造材料的整体结构是多空且疏松的;图1(c,d),热压后的涤纶湿法非织造材料的整体结构变得紧密且孔隙减小。

图1 涤纶湿法非织造材料的扫描电镜图
2 涤纶湿法非织造材料断裂强力的影响工艺分析
2.1 交互性方差分析基本理论
交互性方差分析需要假定在不同水平组合下样本相互独立[20],且Xijk~N(μijk,σ2),i,j,k=1,2,3。其中i,j,k分别表示为热压温度、热压压力以及热压时间的水平。记为

称μ为一般平均,αi为热压温度的第i个水平的效应,βj为热压压力的第j个水平的效应,γk为热压时间的第k个水平的效应,显然满足关系式[20]
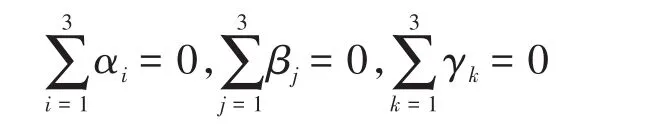
若μijk≠μ+αi+βj+γk,则μijk-μ-αi-βjγk=τij+λjk+ωik+θijk,其中,τij为热压温度的第i个水平与热压压力的第j个水平的交互效应;λjk为热压压力的第j个水平与热压时间的第k个水平的交互效应;ωik为热压温度的第i个水平与热压时间的第k个水平的交互效应;θijk为热压温度的第i个水平与热压压力的第j个水平以及热压时间的第k个水平的交互效应,则数学模型如下:
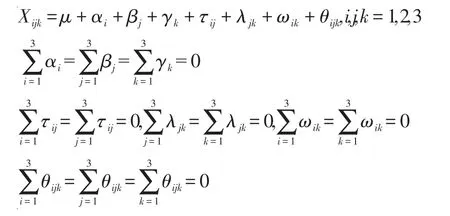
现假设检验为:
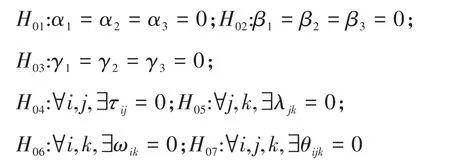
2.2 影响工艺分析
为了更好的分析控制因素以及它们之间的交互作用对非织造材料断裂强力的影响,选择运用热压温度、热压压力、热压时间、热压温度*热压压力、热压温度*热压时间、热压压力*热压时间以及热压温度*热压压力*热压时间的方差分析对涤纶湿法非织造材料断裂强力进行显著性检验,检验结果见表2。
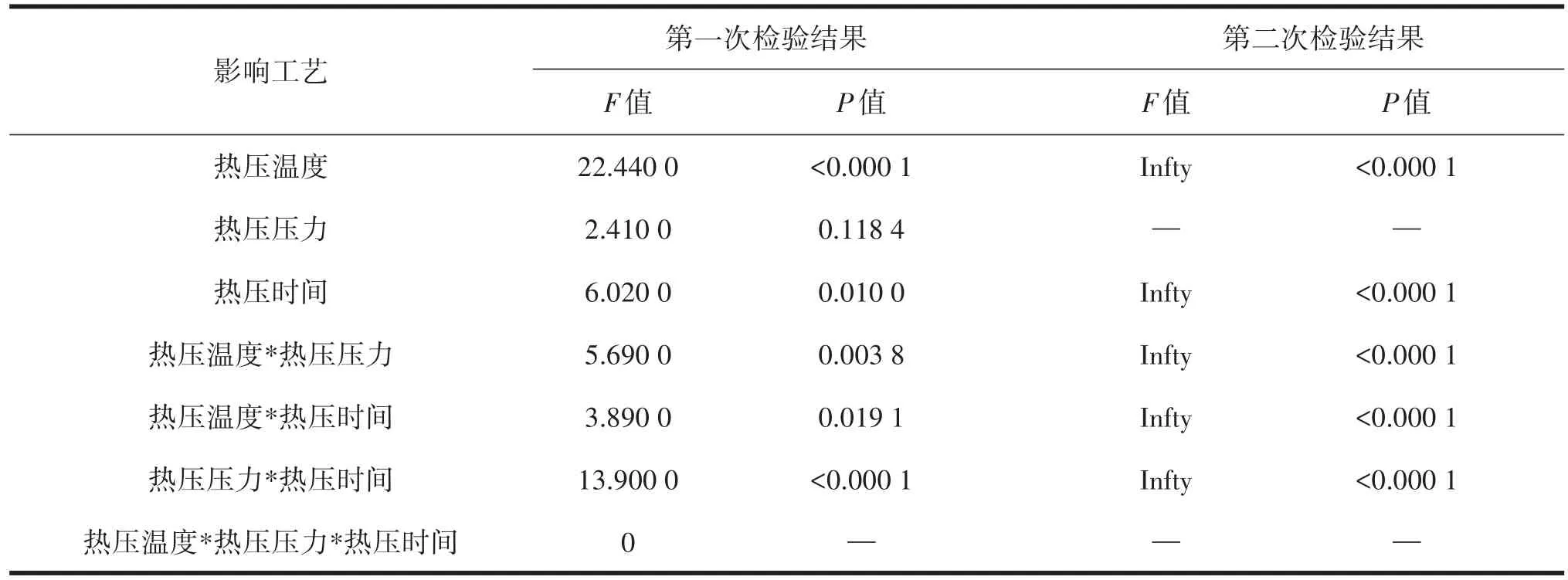
表2 热压参数对断裂强力的显著性检验结果
表2中第一次检验结果表示全因素检验结果,第二次检验结果表示去掉“热压压力”、“热压温度*热压压力*热压时间”交互的显著性检验结果。表2的第一次检验结果表明:“热压温度”、“热压时间”、“热压温度*热压压力”、“热压温度*热压时间”以及“热压压力*热压时间”,它们的P值均小于0.05,所以这些因素均对涤纶湿法非织造材料断裂强力具有显著性影响;“热压压力”的P值大于0.05,因此“热压压力”对湿法非织造材料断裂强力没有显著性影响;“热压温度*热压压力*热压时间”的F值为0,P值计算不出,无法说明“热压温度*热压压力*热压时间”对断裂强力是否有影响。
表2中第一次检验结果还能说明它们对断裂强力有显著性影响因素的主次效应。从表2中可知,“热压温度”对应的F值为22.44,“热压压力”对应的F值为2.41,“热压时间”对应的F值为6.02,“热压温度*热压压力”对应的F值为5.69,“热压温度*热压时间”对应的F值为3.89,“热压压力*热压时间”对应的F值为13.9。F值越大就越说明影响就越重要,因此主效应排序依次是“热压温度”、“热压压力*热压时间”、“热压时间”、“热压温度*热压压力”、“热压温度*热压时间”、“热压压力”。
“热压温度*热压压力*热压时间”的F值、P值出现异常的情况,选择利用SAS软件检验“热压温度”、“热压压力”、“热压时间”三者之间的相关性,结果表明:“热压温度*热压压力”与“热压温度*热压压力*热压时间”、“热压时间*热压压力”与“热压温度*热压压力*热压时间”、“热压温度*热压时间”与“热压温度*热压压力*热压时间”这三对之间是相关的。因此,“热压温度*热压压力*热压时间”可以由“热压温度*热压压力”、“热压温度*热压时间”、“热压时间*热压压力”表示,故“热压温度*热压压力*热压时间”可以忽略。去掉“热压压力”、“热压温度*热压压力*热压时间”重新检验,得到最终的检验结果见表2的第二次检验结果。
表2的第二次检验结果表明:“热压温度”、“热压时间”、“热压温度*热压压力”、“热压温度*热压时间”以及“热压压力*热压时间”F值均是无穷大,P值均小于0.000 1,小于0.05,因此“热压温度”、“热压时间”、“热压温度*热压压力”、“热压温度*热压时间”以及“热压压力*热压时间”均对湿法非织造材料断裂强力有显著性影响。
3 涤纶湿法非织造材料断裂强力的热压工艺优化控制
3.1 正交回归设计基本理论
正交回归设计是指试验方案的结构矩阵具有正交性的回归设计,是在正交设计基础上发展起来的,可建立方程。其突出优点是用很少的处理组合得出完全试验相同项数的回归模型,计算过程极为简单并已消除了回归系数之间的相关性,统计性质得到了明显改善。
对于正交回归模型,其中包括常数项、线性项、线性交互作用项及二次项,在该文中将热压温度、热压压力和热压时间作为自变量。需要说明的是,由影响工艺分析发现,热压压力对湿法非织造材料断裂强力没有显著影响,因此这里不考虑热压压力以及热压压力自身的交互,但是由于热压温度、热压时间对其有显著性影响,这里认为热压温度和热压压力的交互、热压时间和热压压力的交互是有影响的,因此得出二次正交回归模型为:
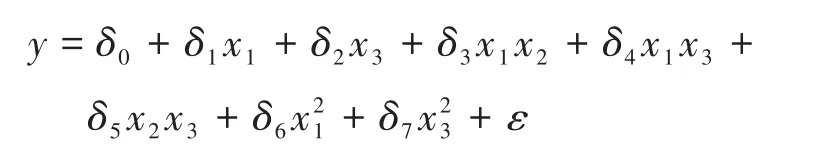
其中,δl(l=0,1,…,7)表示回归系数;x1,x2,x3分别表示热压温度、热压压力、热压时间;两者的乘积表示其交互效应,比如:x1,x2表示热压温度和热压压力的交互效应;ε表示误差。用y表示断裂强力。
3.2 最优热压工艺控制点的计算
运用SAS软件,建立了正交回归方程,并对模型和回归系数进行了显著性检验,详见表3。
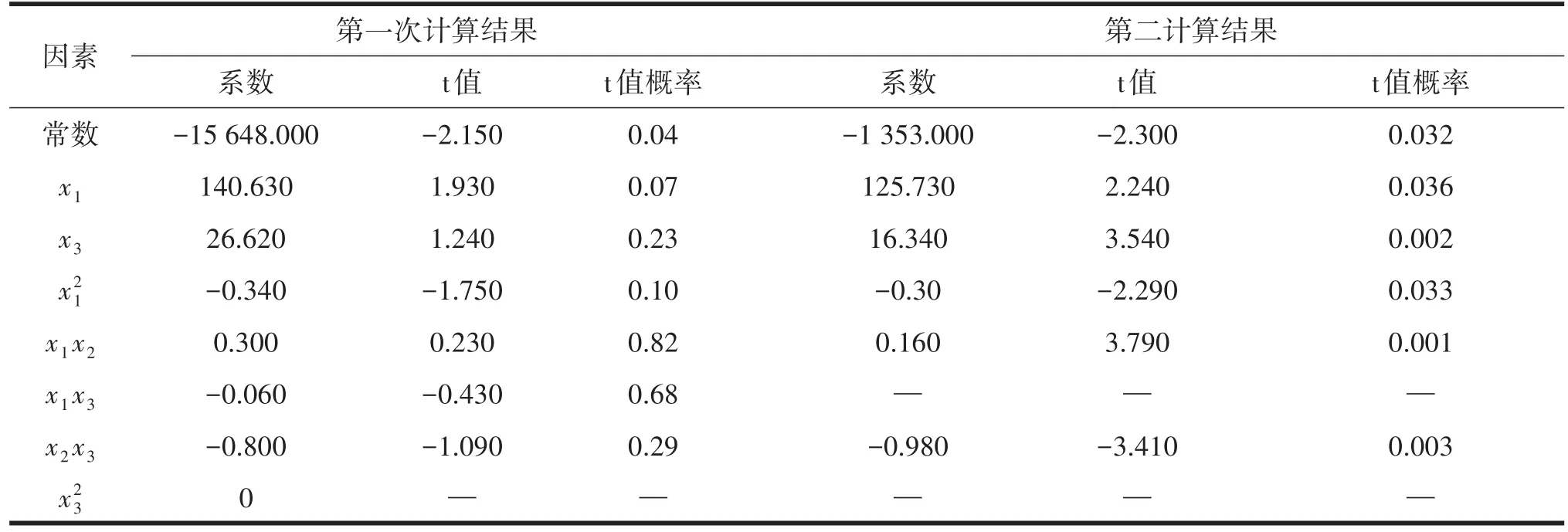
表3 断裂强力的二次正交回归方程
表3第一次计算结果表示初步的二次正交回归方程,第二次计算结果表示最终的二次正交回归方程。表3的第一次计算结果发现,对应的系数为0,而t值以及它的概率均没有显示,这是由于它可以由其他的因素表示出来,即
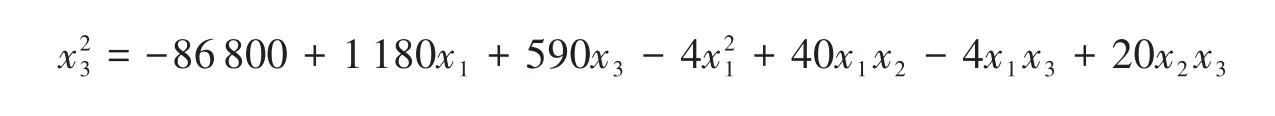
该方程表明它与其他各个因素都存在着相关性。因此,需要重新调整模型,不考虑热压压力、热压温度与热压时间之间的交互、热压压力与自身的交互以及热压温度,热压压力和热压时间三者之间的交互,得到新的二次正交回归模型(见表3的第二次计算结果)。
为了进一步优化涤纶湿法非织造材料断裂强力,这里给出优化模型(目标函数和约束条件)来求解最佳控制点以及涤纶湿法非织造材料的最大断裂强力。具体模型如下所示:
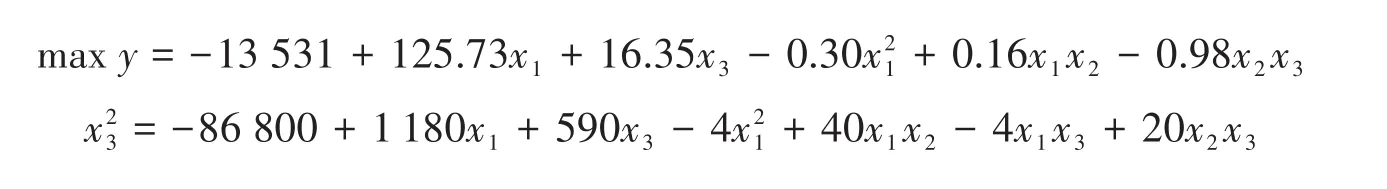
利用LINGO软件求解,得到x1=206.55℃,x2=15.17 Pa,x3=48.63 s,y=80.87 N,即在热压温度为206.55℃,热压压力为15.17 Pa,热压时间为48.63 s时,材料最大断裂强力为80.87 N。
3.3 实验验证
为了验证理论结果的正确性,本文进行了实验验证。首先,在纤维标准解离器的槽桶内中加入2250 mL水、2 mL 0.5% PEO分散剂以及6:4比例的1.507 g PET-260纤维和1.005 g PET UDY纤维,启动解离器分散纤维以形成纤维悬浮液。其次,将悬浮液倒入纸页成型器的容器中以排干绝大部分水形成湿的纤维网,将湿纤网在100°C下干燥10 min形成涤纶湿法非织造材料。然后,通过平板热压机在x1=206.55 ℃ ,x2=15.17 Pa,x3=48.63 s,y=80.87 N条件下对涤纶湿法非织造材料进行热压粘合从而获得涤纶湿法非织造薄膜。运用万能强力测试仪上进行拉伸实验并记录断裂强力值。
经过上述的实验,可以得到涤纶湿法非织造材料断裂强力为78.9 N。然而理论求得的涤纶湿法非织造材料最大断裂强力为80.87 N,两者数值差距很小,误差大约在2%左右。显示断裂强力的优化控制合理有效。
4 结论与讨论
在对涤纶湿法非织造材料断裂强力建立二次正交回归方程之前,需要利用正交试验得到的实验数据并做方差分析。根据方差分析的结果建立二次正交回归方程,并将正交回归方程作为求解最佳工艺条件的目标函数,通过优化求解得到最佳控制工艺点。这种研究思路和方法可以为其他材料制备提供参考。
运用方差分析研究因素对因变量的影响,因素之间的交互作用是非常重要的。因此需要做重复实验研究它们之间的交互作用。交互作用可以为建立正交二次回归提供参考,从而减少回归自变量个数,降低模型建立的难度。
寻找最佳工艺条件,也可以尝试用其他方法,如更高次数的回归。但这需要更多的实验数据,对实验的要求也随之提高。在实验数据不变的情况下,选择其他非线性回归也是一个尝试,如对数线性回归、半对数线性回归等。
对湿法非制造材料断裂强力进行优化控制,是为了得到断裂强力最好的涤纶湿法非织造材料,这有利于在此基础上制备性能更好的膜,使得制备非织造材料的质量达到最佳,以便在纺织行业得到更好的应用。

