含白噪声的随机糖酵解化学反应模型的动力学行为

李丹彤，杨 颖

(长春师范大学数学学院，吉林 长春 130000)

1 预备知识

糖酵解是一种通过代谢过程将葡萄糖转化为丙酮酸的生化反应，是活细胞利用葡萄糖获得能量的方法.文献[1]给出了一个基本模型，它可以通过以下两个耦合的一阶微分方程[2]来表示：

(1)

其中：x和y分别表示二磷酸腺苷(ADP)和磷酸果糖(F6P)的浓度；参数(α，β)非负.方程(1)为无量纲化之后的形式，容易看出P(β，β/(α+β2))是系统(1)的唯一正平衡点.如果适当选择参数α和β，系统(1)存在一个稳定的极限环[3].此外，有关糖酵解数学模型的细节可见文献[4-6].文献[7-9]扩展了对于糖酵解模型的分支分析和定性性质的研究.文献[10]构造了一个非标准差分形式，利用离散时间模型的极限环行为证明了解的正性.文献[11]讨论了离散时间模型的定性行为、分岔分析和混沌控制.

本文旨在研究随机糖酵解模型的动力学行为.最近通过研究一些随机化学反应模型得到了它们的遍历性[12-14].显然，生化反应模型不可避免地会受到环境白噪声的影响.反应中的催化剂、溶剂、温度等因素都会对反应过程产生影响，因此在化学反应中考虑随机扰动是合理的.现将确定性糖酵解模型(1)加入白噪声系统扰动，将其转化为伊藤随机微分方程：

(2)

首先给出一些常用的记号和公式.在本文中，令

除非另行说明，总假设(Ω，F，{Ft}t≥0，P)为满足通常条件(右连续且F0包含所有的零测集)的带有域流{Ft}t≥0的完全概率空间.下面考虑给定初始值x(t0)=x0∈R+的d维随机微分方程：

dx(t)=f(x(t)，t)dt+g(x(t)，t)dB(t)，t>t0.

(3)

LV(x，t)=Vt(x，t)+Vx(x，t)f(x，t)+1/2trace[gT(x，t)Vxx(x，t)g(x，t)].

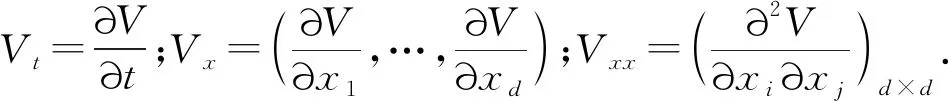
dV(x(t)，t)=LV(x(t)，t)dt+Vx(x(t)，t)g(x(t)，t)dB(t).

2 正解的存在唯一性

首先说明系统(2)的解是正的和全局的.对于任意初始值，为了得到唯一的全局解，即解在有限时间内不会爆破，方程的系数被要求满足局部Lipschitz条件和线性增长条件[15].然而随机系统(2)中的xy2项是非线性的，因此系统(2)的系数显然不满足线性增长条件.这样解可能会在有限时间内爆破.这里利用Lyapunov分析方法，说明系统(2)的解如文献[16-18]提到的那样是正的和全局的.

定理2.1如果σ1，σ2满足

(4)

P{τn≤T}>ε.

(5)

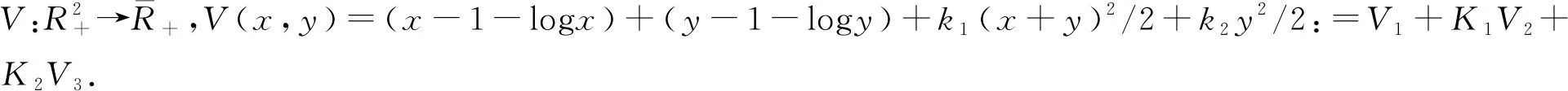
dV(x，y)=LVdt+σ1(x-1)dB1(t)+σ2(y-1)dB2(t)+k1(x+y)(σ1xdB1(t)+σ2ydB2(t))+k2σ2y2dB2(t).

(6)

这里L是系统(2)的生成算子，且有

(7)

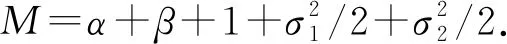
(8)

(9)

由函数V(x，y)的定义及(7)—(9)式，可得

(10)

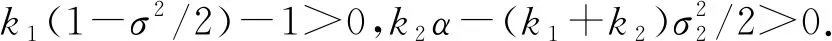
3 遍历性

先给出文献[20]中的一个重要引理，读者也可以参考文献[21].

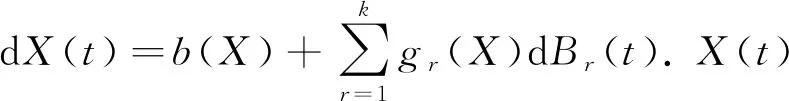
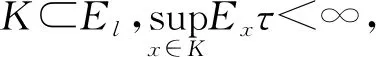
引理3.2设X(t)是El中正则时间的齐次Markov过程.如果X(t)相对于某个有界域U是递归的，那么它相对于El中的任何非空域都是递归的.

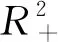
定理3.1如果σ1，σ2满足

(11)

证明为了证明这个定理，需要证明在条件(11)满足的情况下，引理3.1中的条件(B1)和(B2)成立.首先，将系统(2)写成以下形式：

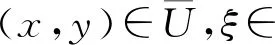
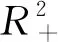
由于条件(11)成立，所以可以取C1，C2，C3为正常数，满足：

(12)

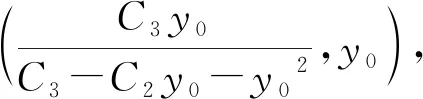
LV≤-(C2+C3-C1β)x-[αC2-β(1+C1)]y-C3β/y-αC3y/x+C3x2+K.

(13)

K-βC3/ε<-1，

(14)

K-αC3/ε<-1，

(15)

K-(C2+C3-C1β)/ε2<-1，

(16)

K-[αC2-β(1+C1)]/ε<-1.

(17)

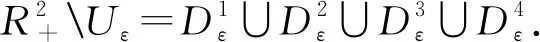
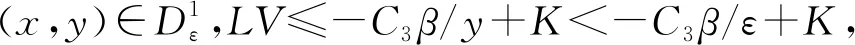
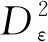
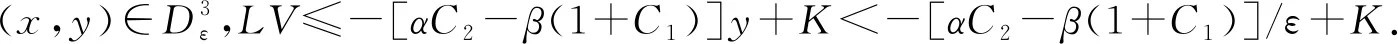
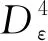
基于对上述情形的讨论，引理3.1中的条件(B2)也满足.这样就完成了定理3.1的证明.

4 数值模拟

假设时间的单位为min，反应物的浓度单位为mol/L.在模型(2)中选取两组不同的参数值，得到了模型(1)和模型(2)的散点分布比较图，并进一步模拟了随机系统的解及其直方图.选取Δt=0.002，使用MATLAB软件进行模拟.

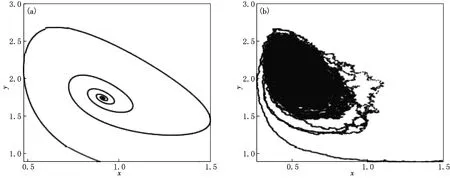
(a)确定性系统(1) (b)随机模型(2)

例4.2系统(2)的参数选取如下：α=0.099，β=0.8，σ1=0.1，σ2=0.1.选取与例4.1相同的初始值，可以计算出P(x*，y*)=P(0.8，0.988).图2给出了常微分模型(1)和相应的随机模型(2)的散点分布对比图.图2表明，系统的稳态周围有一个极限环.

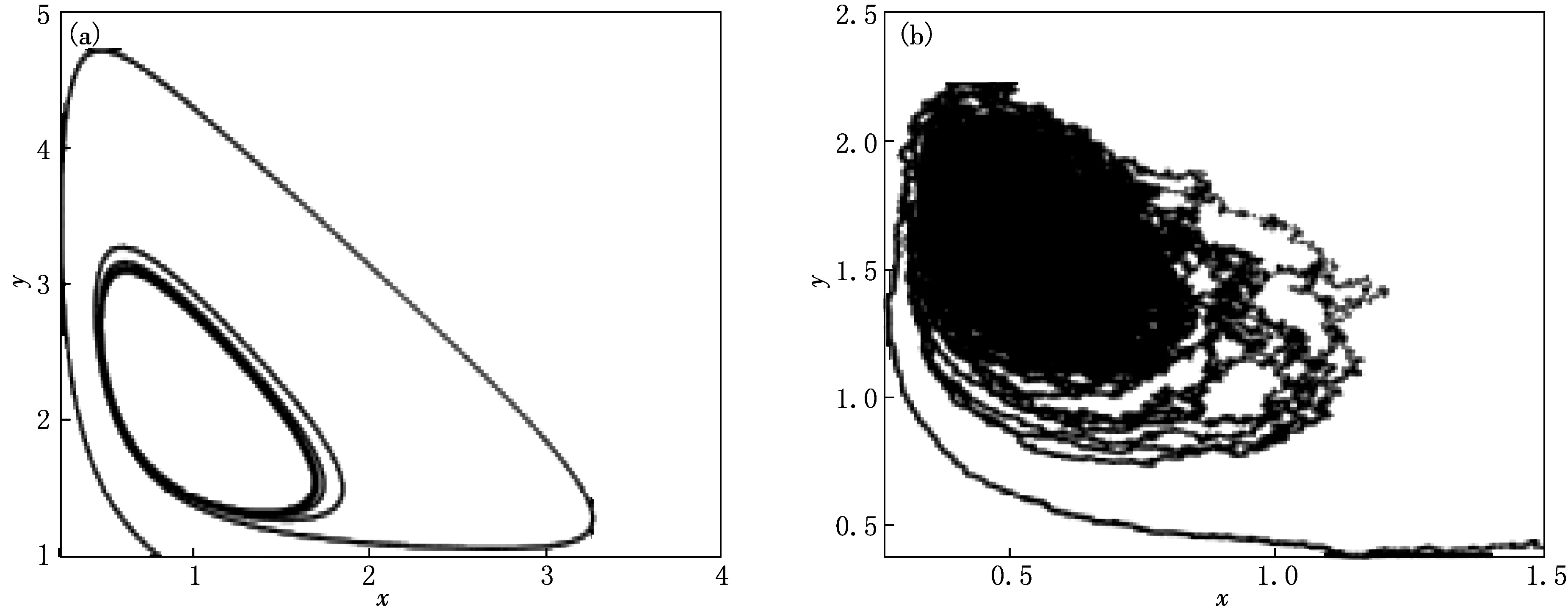
(a)确定性系统(1) (b)随机模型(2)

例4.3系统(2)中参数的选取与例4.1相同，则系统(2)满足定理3.1中的条件(11).由此可得一个平稳分布，见图3右侧的直方图.图3的左图显示系统(2)的解在一个小邻域内波动.

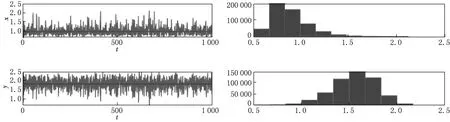
图3 例4.3中随机系统 (2)的解及其直方图

例4.4系统(2)中的参数的选取与例4.2相同，随机系统的模拟结果如图4所示.

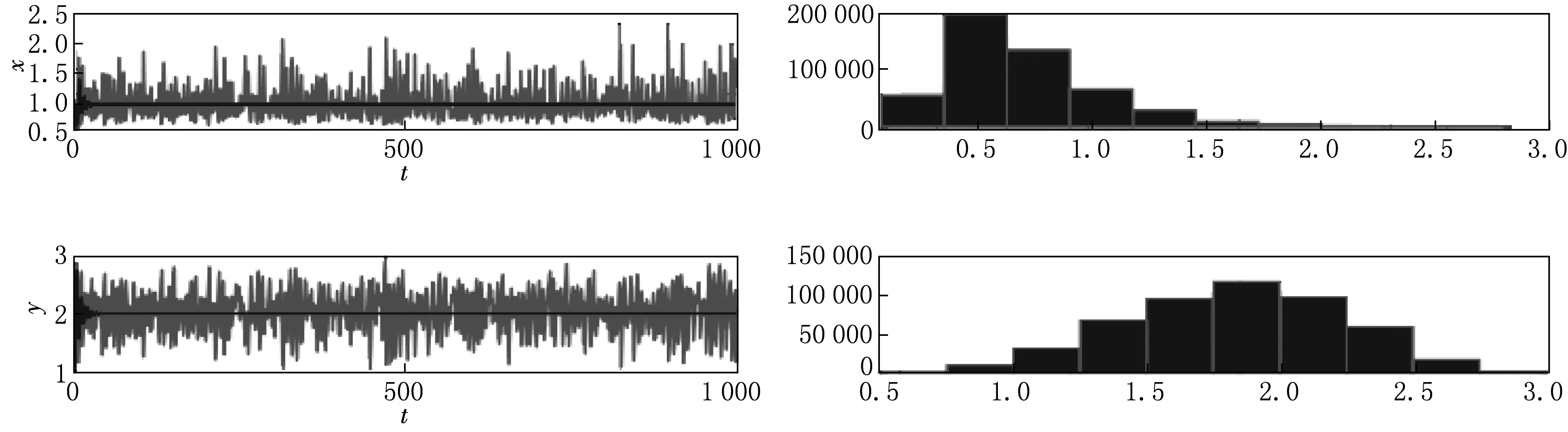
图4 例4.2中随机系统(2)的解及其直方图

从模拟的结果可以看出，确定性系统的稳态有时是稳定的，有时存在极限环.在糖酵解模型中加入随机扰动，会得到一个随机化学的糖酵解模型.如果白噪声的强度满足定理3.1的条件，则无论确定性系统平衡点的形式如何，相应的随机模型都具有遍历性.而且似乎白噪声的加入导致了糖酵解系统的弱稳定性.