删失数据下部分线性模型的贝叶斯P-样条估计
王纯杰,罗琳琳,李纯净,袁晓惠
(长春工业大学数学与统计学院,吉林 长春 130012)
0 引言
近年来,卵巢癌的发病率逐年上升.由于早期卵巢癌不易察觉,故其对女性的身体健康产生了巨大的潜在威胁.由于其发病原因并不明确,因此,对卵巢癌数据的研究具有重大的实用价值.2009年,Cho和Shih[1]对卵巢癌进行了细致描述并给出了针对卵巢癌的一些可用模型;2012年,李阳敏等[2]就早期卵巢癌的诊断数据建立多元线性回归模型,以期找到早期卵巢癌的病理特征;2018年,赫艳玲等[3]对卵巢癌各阶段的治疗方案进行了阐述.
线性回归模型假定响应变量与协变量的关系是线性的,在实际研究中,如果数据的协变量与响应变量的关系为非线性时,线性回归模型的拟合效果较差,于是便产生了易解释且具有更好拟合效果的部分线性模型.部分线性模型最初由Engle等[4]提出,用于研究天气对电力的影响.随后很多学者对此类模型进行了拓展研究.1995年,黄四民和梁华[5]运用部分线性模型分析居民消费结构;2015年,Müller和Geer[6]将部分线性模型拓展到高维情形;2018年,Wu[7]在部分线性模型的DBE(Difference-Based Estimator)估计的基础上进行改进,得到了估计效果更好的DBRE(Difference-Based Ridge Estimator)估计.
在医疗领域,学者们将部分线性模型与生存分析中的删失数据相结合,并对此进行了大量研究.2002年,陈敏和朱力行[8]给出了随机删失数据下的部分线性模型的拟合优度检验;2018年,Wang[9]研究了右删失数据下部分线性模型的经验似然推断.
相比于频率学派,贝叶斯充分利用了先验的信息,在小样本情况下得到了更好的估计效果.2004年,Lang和Brezger[10]首次针对AM(Additive Model)模型提出贝叶斯P-样条,随后此估计方法得到了广泛的运用;2006年,Brezger和Lang[11]将贝叶斯P-样条应用于GAM(Generalized Additive Model)模型;2016年,Bruno[12]等人将贝叶斯P-样条应用于完整数据的部分线性模型;2018年,William和Gholamreza[13]将贝叶斯P-样条应用于RSM(Risk-Sharing Model)模型.
本文基于贝叶斯P-样条,针对右删失数据,运用部分线性模型分析一些因素对卵巢癌患者生存时间的影响,得到了有效的参数估计,为卵巢癌的防治提供了有效建议.
1 部分线性模型及贝叶斯P-样条
部分线性模型最初由Engle等[4]提出,由于其可以处理非线性关系,因此具有很高的灵活性,其模型如下:
log(T)=g(Z)+αTX+ε.
其中:T为响应变量;X为p维变量;Z为一维变量;g(·)是未知函数;α为p维变量X的系数;ε为随机误差,满足Eε=0,Eε2=σ2,其分布可取标准正态分布(Normal)、标准极值分布(Extreme)和标准逻辑斯谛分布(Logistic).
在生存分析中很难得到完整的数据,所以需要处理不完整数据,其中最为常见的为右删失数据.令事件发生的确切时间为T,但一些病人在实验结束后要观察的事件仍然没有发生,只知道事件发生的时间大于删失点C.用δ=I(T≤C)表示数据是否删失,故得到Y=min(T,C)的观测数据,其数据结构为D={Y,δ,X,Z}.
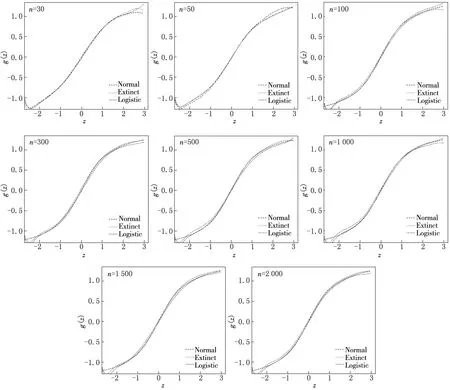
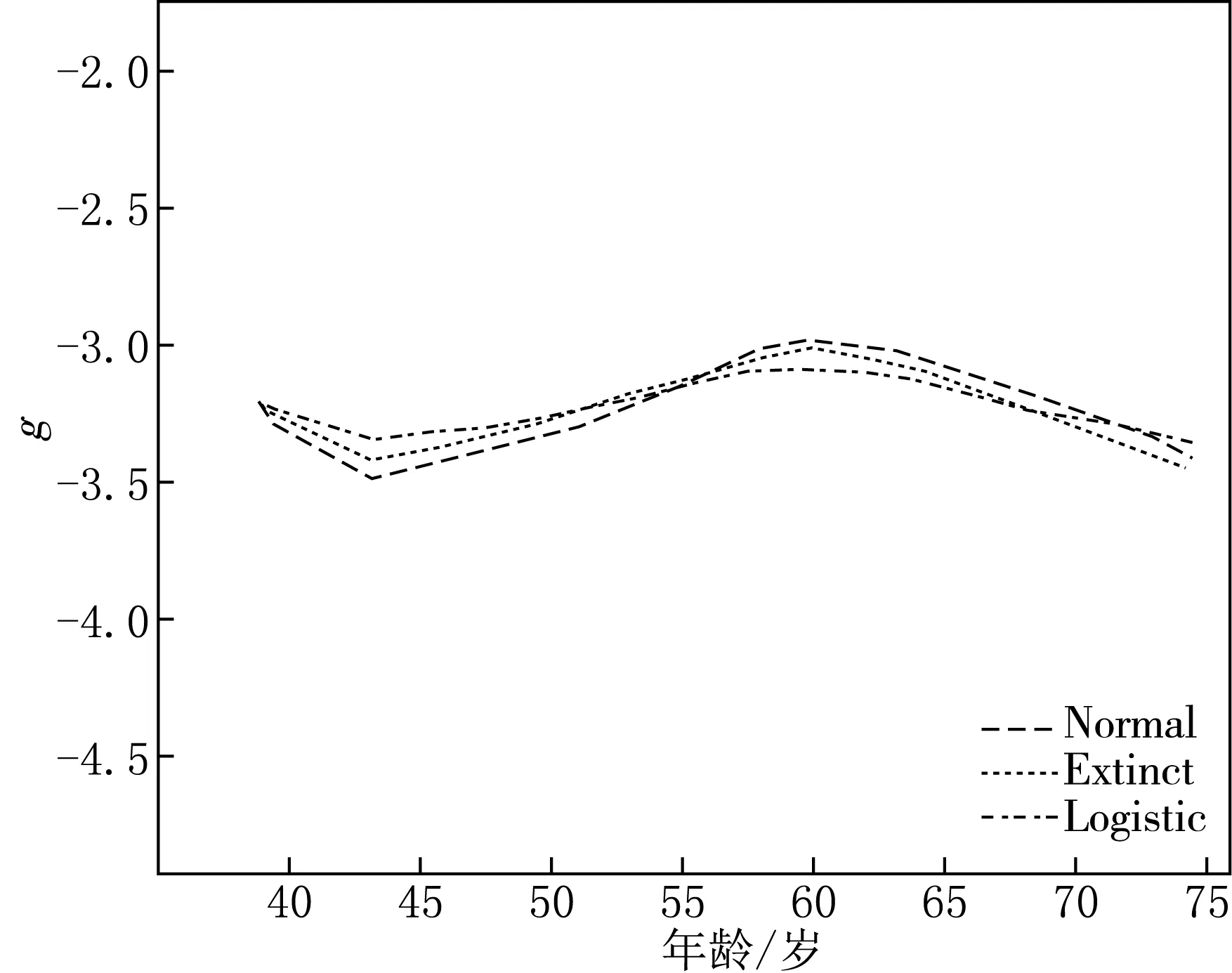
部分线性模型中较为重要的部分在于如何估计非参数部分g(Z).自从部分线性模型提出后,出现了许多关于g(Z)的估计方法,如样条估计、核估计、M估计等.在这些方法中较为成熟的估计方法是B-样条估计.在B-样条中假定协变量的定义域为[a,b],将协变量分成m段,a=k0 其中B(Z)为样条基函数,其定义为 在B-样条中,当m很大时,容易出现过拟合现象.为了确保其有效性,1996年Eilers和Marx[14]提出了P-样条,即在每个样条基函数的系数上定义一个粗略的惩罚项以保证拟合出的曲线充分光滑.根据Eilers和Marx[14]的文章得到的惩罚似然函数如下: 其中:Δtβ为β的t阶差分;f(yi|Xi,Z,β,α)为在给定Xi,Z,β的条件下Yi的密度函数;F(Yi|Xi,Z,β,α) 为给定Xi,Z,β的条件下Yi的分布函数.在标准正态分布、标准极值分布和标准逻辑斯谛分布下的似然函数如下: P-样条在处理大样本问题中具有很高的有效性,且相比于B-样条而言,节点的选择对估计的影响较小.但样本量不够多时,P-样条的估计效果并不理想,于是Lang和Brezger[10]在P-样条的基础上加入了贝叶斯,得到的贝叶斯P-样条方法在样本量较小时仍有很好的估计效果.根据Lang和Brezger[10]的文章,对系数β取如下二阶差分: βj=2βj-1-βj-2+ωj. 其中ωj~N[0,τ/ψ],τ用于保证函数的平滑度,ψ用于保证每一段上的曲率是不同的.根据Song等[17]的研究结果,非线性部分有如下约束: 故在贝叶斯部分,对β取有约束的高斯先验,各参数的先验分布如下: 在模拟与实例中假定样条的段数m=18,差分阶数t=2,参考文献[10],取α1=1,α2=0.005,v=1,α0=0.5,ϑ=1.由此得出参数的后验如下: τ-1~Gamma(α1+(m-t)/2,α2+βTM(ψ)β/2), ψ~Gamma((v+m-t)/2,v/2+(βj-2βj-1+βj-2)/2τ), (1) 给定初值α0,β0. (3) 从U(0,1)中抽取u1t,若 则αt=α(new),否则αt=αt-1. β(new)=β(e)-B(BTB)-1BTβ(e). (5) 从U(0,1)中抽取u2t,若 则βt+1=β(new),否则βt+1=βt. 重复循环10 000次,为去除初始值的影响去掉开始的5 000次抽样结果.剩余5 000次循环结果的均值即为β和α的估计值. 通过模拟检验贝叶斯P-样条在删失数据部分线性模型下的估计效果.部分线性模型的具体形式如下: log(T)=g(Z)+αX+ε. 其中:g(z)=arctan(z),Z~U(0,1),α=2,X为成功概率为0.5的伯努利分布随机数.对误差ε取3种不同的分布(见表1). 表1 误差分布 令删失比为40%,算得3种情况下的删失点分别为C=αX+g(Z)+U[0,0.15],C=αX+g(Z)+U[0,0.02],C=αX+g(Z)+U[0,0.1].考虑不同样本量的右删失数据.用来衡量α的估计好坏的指标为偏和均方误差.具体计算结果见表2. 表2 两种不同方法的估计效果比较 由表2的结果可以看到,贝叶斯P-样条方法在不同的误差分布下α均拥有较小的bias与MSE,且样本量越大,bias与MSE的值越小.说明在不同的误差分布下部分线性模型的参数部分拟合效果很好.而用B-样条方法时,当样本量较大时的估计效果与贝叶斯P-样条结果类似,但在样本量较小时贝叶斯的估计效果要优于B-样条的方法,说明贝叶斯方法要优于普通的B-样条方法.取不同误差分布的贝叶斯P-样条非参数的g(Z)部分的拟合结果如图1所示.图2为B-样条方法得出的曲线图.对比图1—2可以看出,贝叶斯P-样条的拟合图像具有较好的拟合效果,而B-样条在前端与真实曲线相差较大,且贝叶斯P-样条估计出的曲线更为平滑.由此可以看出贝叶斯P-样条得到的曲线更光滑且样条节点的选择对其影响更小. 图1 贝叶斯P-样条下g(z)的拟合图 本文将部分线性模型的贝叶斯P-样条估计应用于一个医学问题中.数据来自于Edmunson等[16]的研究,该研究记录了对患卵巢癌的女性进行两种不同的治疗(化疗与放疗加化疗)的疗效,结合患者的自身因素,分析了不同的治疗方案以及患者自身因素对卵巢癌患者生存时间的影响.该研究共收集了26例卵巢癌病人的有效数据,删失比为46%.选取4个影响因素:患者的年龄X1,患者对治疗的耐受能力X2,治疗方案X3,患者是否有其他疾病X4.对生存时间的对数log(T)采用部分线性模型建模,非参数部分运用贝叶斯P-样条的方法进行拟合. 图2 B-样条下g(z)的拟合图 先对4个变量进行筛选,用生存时间的对数对4个协变量建立加速失效模型,结果见表3.由于发现有些变量的P值大于0.05,故进行逐步回归筛选变量.逐步回归结果见表4,逐步回归过程剔除了患者对治疗的耐受能力X2与患者是否有其他疾病X4,保留的患者的年龄与治疗方案均有较小的P值,故接下来用这两个变量建模. 表3 AFT模型估计结果 表4 逐步回归后估计结果 患者年龄与生存时间对数图像见图3.由图3可知,患者的年龄与生存时间的对数之间存在非线性趋势,故令Z为患者的年龄,X为治疗方案,建立如下部分线性模型: log(T)=g(Z)+αX+ε. 由于误差ε的分布未知,故分别选取标准正态分布,标准极值分布与标准逻辑斯谛分布进行拟合.线性部分治疗方案的系数估计结果见表5. 表5 线性部分治疗方案系数的估计 非线性部分的拟合结果见图4. 图4 g(·)的拟合图 在有可能影响卵巢癌患者生存时间的4个因素中,年龄与治疗时采取的治疗方案对卵巢癌患者的生存时间影响显著.对误差分布取3种不同的形式建立部分线性模型.其中治疗方案对卵巢癌患者生存时间的影响是线性的,且呈正相关,即化疗的治疗方法比化疗加放疗的治疗方法好,可更好地延长患者的寿命.年龄对卵巢癌患者生存时间的影响呈现非线性关系,这也符合客观规律.由图4可知60岁以下卵巢癌患者的生存时间与年龄成正比,而60岁以上的卵巢癌患者生存时间与年龄成反比. 本文运用部分线性模型的贝叶斯P-样条估计方法分析了卵巢癌数据,在模拟中贝叶斯P-样条方法拟合的未知曲线更为光滑且其具有较小的bias和MSE.因此贝叶斯P-样条方法可用在部分线性模型中对未知曲线进行拟合. 卵巢癌大多发生在40岁以上的女性身上,且未婚未育女性发生卵巢癌的几率更大.卵巢癌若早发现,早治疗,痊愈的概率很大,但老年人由于年龄的增长,身体各项机能减弱,患病后很难痊愈,所以在实例中得出的结论是正确的.即对卵巢癌患者生存时间影响显著的两个变量是治疗方案与患者年龄.其中患者年龄与卵巢癌患者的生存时间呈现非线性关系:当年龄小于60岁时,年龄与生存时间成正比;当年龄大于60岁时,年龄与生存时间成反比.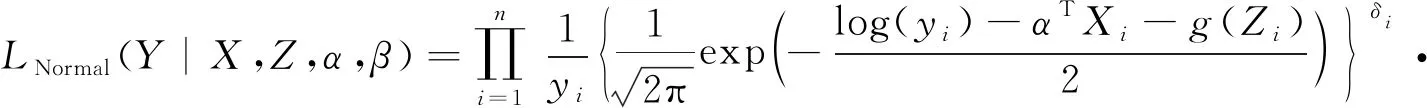
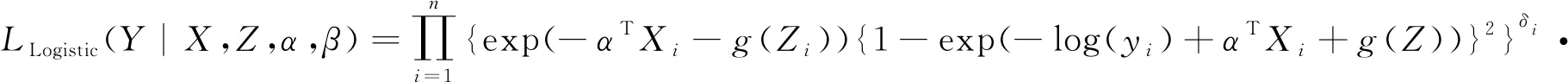
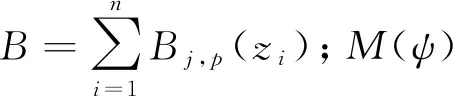
2 MCMC算法

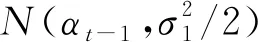
3 模拟研究


4 实证研究




5 总结

