随机种群模型的平稳分布和数值模拟
付 静,魏丽莉,陈 岩
(长春师范大学数学学院,吉林 长春 130031)
1 预备知识
20世纪40年代,Leslie[1]提出:捕食者的环境容纳量与食饵的数量成正比;捕食者和食饵的增长率都有一个上限,对于捕食者来说,当食饵与捕食者的比例充分大时达到上限,对于食饵来说,当捕食者的数量充分小时达到上限;给出了著名的捕食-食饵模型
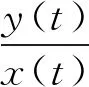
(1)
其中α1是正常数.给出了:系统(1)存在唯一的正平衡点;如果其是局部渐近稳定的,那么它是全局渐近稳定的.
为了方便计算,Huang等[13]将模型转化为如下形式:
(2)

由于现实环境中会受到很多因素的影响,越来越多的学者研究了随机种群模型,而生物种群模型的确定性忽视了环境噪声的干扰,依据中心极限定理知,这种扰动可以由均值为零的正态分布来刻画[14].本文根据文献[15]的方法添加了随机因素
其中:B1(t),B2(t)是独立的白噪声;σi>0(i=1,2)代表噪声强度.得到了如下随机捕食-食饵模型:
(3)
因为随机种群模型没有内部平衡点,所以不能像确定性模型那样通过讨论内部平衡点的稳定性来确定随机种群的持久性.随机系统的平稳分布是一种弱稳定性,遍历性表示时间均值意义下随机系统是持久的.因此研究随机系统的平稳分布和遍历性具有非常重要的意义.本文研究了随机系统(3)的平稳分布,并且将结果与确定性模型进行了比较,给出了两种模型的数值模拟.
下面给出文中需要的几个重要结论:
定理1(伊滕公式)[16-17]设X(t)(t≥t0=0)是方程(13)的解,V∈C2,1(Rn×R+;R).则V(X(t),t)仍是一伊滕过程,且满足随机微分方程:

(4)
称此公式为伊滕公式.
定理2(随机比较定理)[16-18]设Xi(t)(i=1,2)是随机微分方程
dXi(t)=fi(Xi(t),t)dt+ɡ(Xi(t),t)dB(t)
的解,其中:f(X,t)∈C([0,∞)×R),ɡ(X,t)∈C([0,∞)×R).如果:
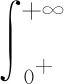
|ɡ(X,t)-ɡ(Y,t)|≤ρ(|X-Y|),X,Y∈R,t≥0;
(2)f1(X,t)≤f2(X,t),X∈R,t≥0;
(3)X1(0)≤X2(0).
则对t≥0有
X1(t)≤X2(t),a.s..
定理3(随机系统的平稳分布)[19]设X(t)是El中的一自治Markov过程,满足下面的随机微分方程:

(5)
其扩散阵为
假设存在具有正则边界的有界区域U⊂El满足下列条件:
(A1)在U和它的一些邻域内,扩散阵Λ(x)的最小特征值是非零的;
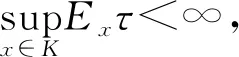
令f(·)是关于测度μ可积的函数,则对所有的x∈El,有下面的公式成立:
验证(A1)成立,只需证明F在U中是一致椭圆的,其中Fu=b(x)·ux+1/2tr(A(x)uxx),即证存在正数M,满足
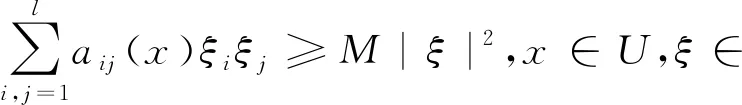
验证(A2)成立,只需证明存在非负C2类函数和邻域U使得对任意EU,LV是负的.
2 随机系统(3)的遍历性
假设(Ω,F,P)是完备的概率空间.考虑F的部分σ-代数构成的类{Ft}t≥0,如果下列条件成立:
(1) 当s≤t时,Fs⊂Ft;
则称这个类是(Ω,F,P)上的一个流.若它是单调递增右连续的,且F0包含所有的零测集,则称流{Ft}t≥0满足通常条件.在本文中所有研究都在赋予流{Ft}t≥0的概率空间进行.
由于系统的解表示捕食者和食饵的密度,因此只考虑正解的存在性.对于任何给定的初始条件,方程的系数需要满足线性增长条件和局部Lipschitz条件[16],这是方程存在唯一全局解的必要条件.然而系统(3)的系数既不满足线性增长条件,也不是局部Lipschitz连续的.首先通过下面引理1,利用伊滕公式和随机微分方程比较原理,可得到系统(3)的解是全局非负的.

证明考虑如下扩散过程:
(6)
由于方程(6)的系数是局部Lipschitz连续的,则对于任意给定的初始条件u(0)=lnx(0),v(0)=lny(0),在t∈[0,τe)中存在一个唯一的局部解,其中τe是爆破时间[16].则系统(6)存在一个唯一的局部解x(t)=eu(t),y(t)=ev(t),只需证明其是全局的.考虑如下两个随机微分方程:
(7)
(8)
设其满足初始条件Φ(0)=φ(0)=x(0)和Ψ(0)=ψ(0)=y(0),则方程(7)和(8)的解分别为
利用随机微分方程的比较原理,得到
φ(t)≤x(t)≤Φ(t),ψ(t)≤y(t)≤Ψ(t) a.s.,
对于t≥0成立,则唯一局部正解是全局的.
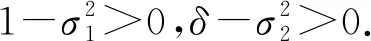
证明
得到扩散矩阵
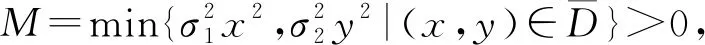

从而定理3的条件(A1)成立.下面需要证明定理3的条件(A2)成立.为了方便,把(x(t),y(t))记为(x,y).定义一个C2-函数V:R2→R+如下:
V(x,y)=1/x+q/y+x+Qlogy-Qlogq/Q,
(9)
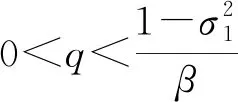
考虑有界集
则
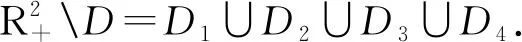
其中:
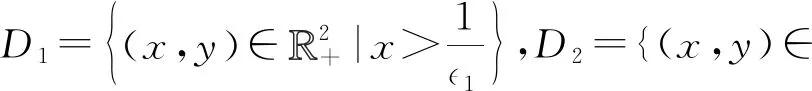
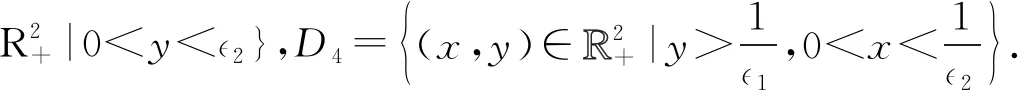
(10)
(11)
(12)
(13)
K在后面被定义.下面分4种情况进行讨论:
情况1当(x,y)∈D1时,得到
其中
(14)
由(10)式得LV≤-1.
情况2如果(x,y)∈D2,则
由(11)式得LV≤-1.
情况3如果(x,y)∈D3,有
由(12)式得LV≤1.
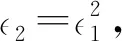
由(13)式得LV≤-1.
从而证明了定理3的条件(A2)成立,因此随机系统(3)有唯一的平稳分布μ(·),且是遍历的.定理证毕.
3 随机系统(3)的灭绝性

4 随机系统(3)的数值模拟
这里用文献[22]中的方法,借助于Matlab软件来验证本文的结果.随机系统(3)的离散化方程为
其中ξk和ηk(k=1,2,…,n)是服从N(0,1)分布的独立Gaussian随机变量.根据文献13]中引理2.1,将分3种情况讨论噪声对种群的影响.
情况1选取适当的参数,使得确定性系统(2)中的Δ>0,那么确定性系统(2)存在唯一的正平衡点,白噪声只要足够小,那么随机系统存在遍历的平稳分布.

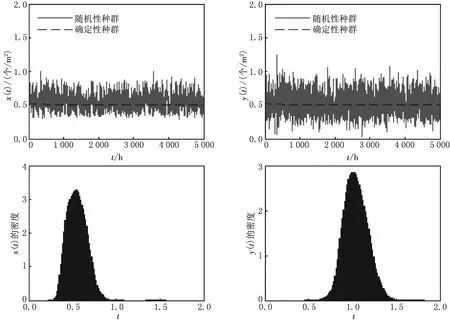
图1 给定初始值(x0,y0)=(0.5,0.5),取参数d1=8,m1=-5,δ=3,β=3,σ1=0.1,σ2=0.1
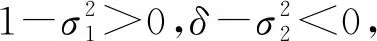
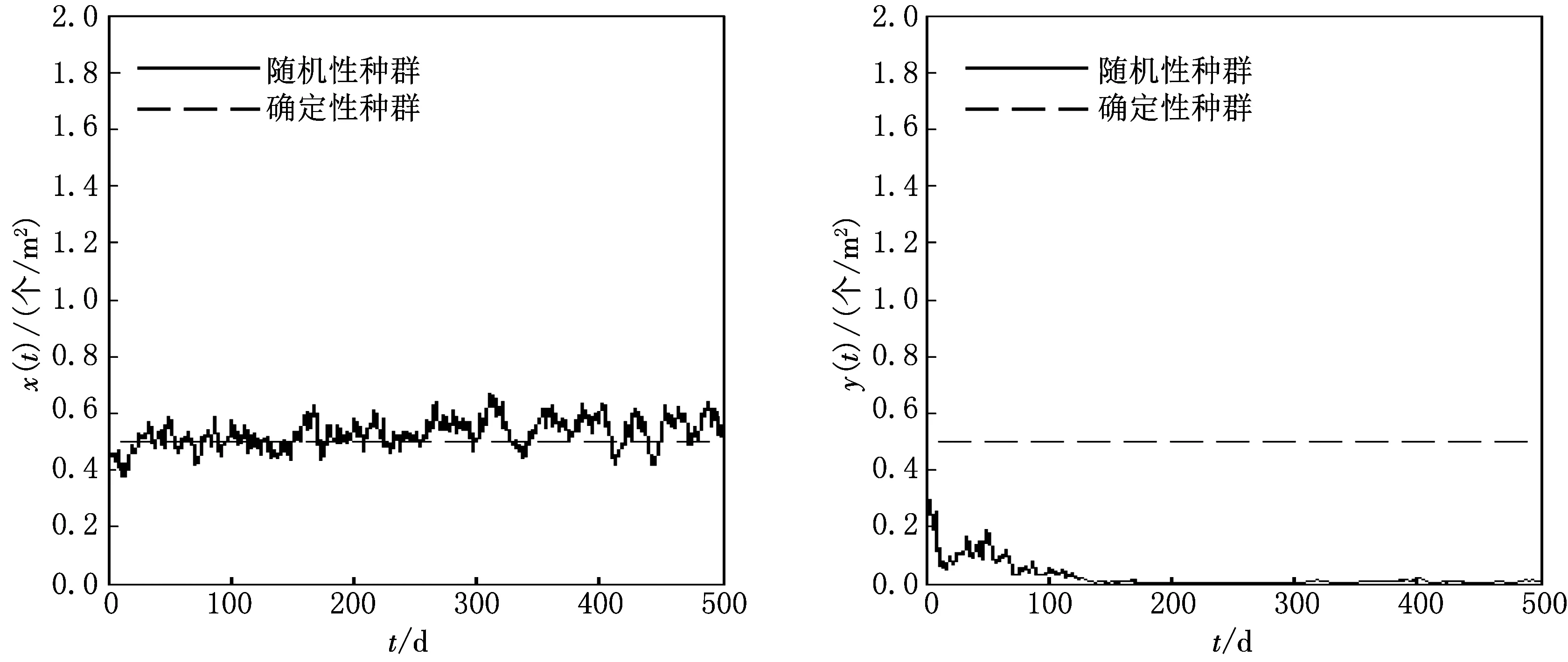
图2 给定初始值(x0,y0)=(0.5,0.5),取参数d1=8,m1=-5,δ=3,β=3,σ1=0.01,σ2=1.8
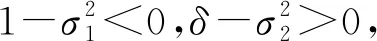
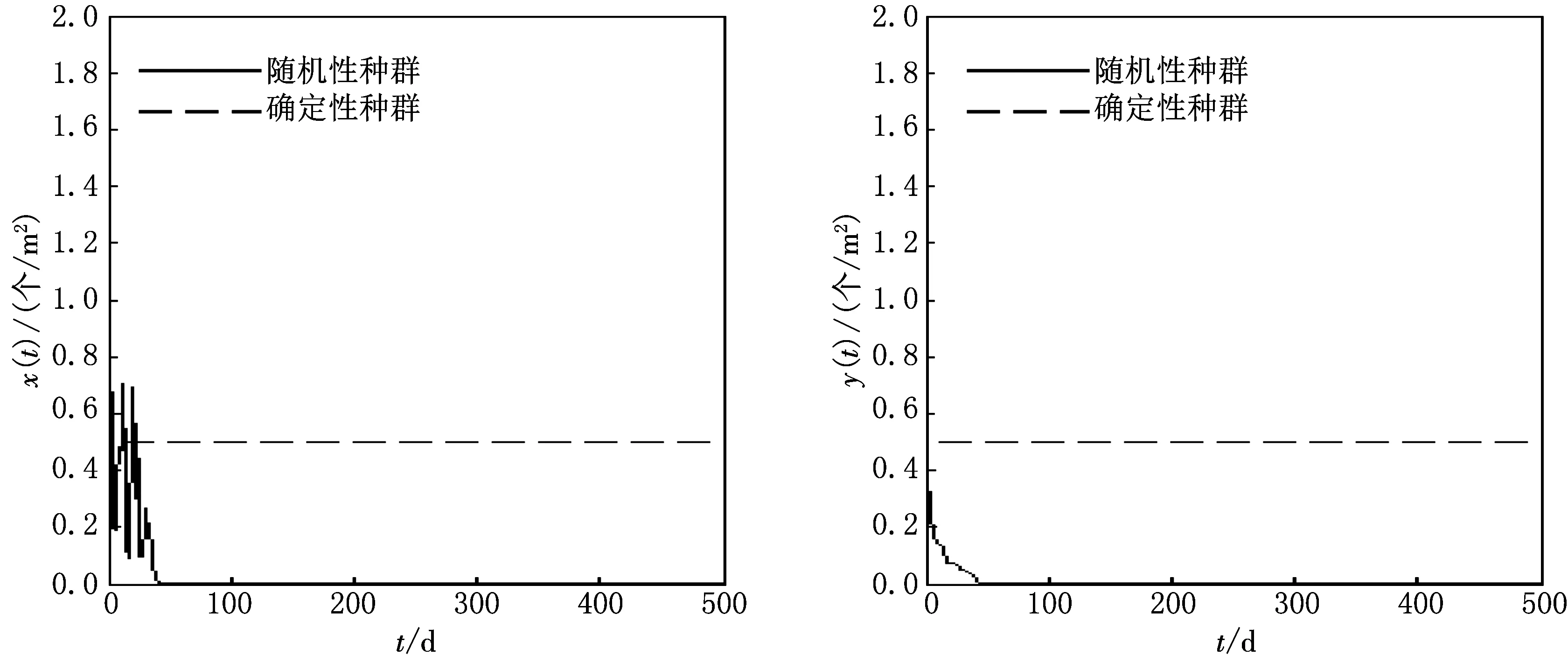
图3 给定初始值(x0,y0)=(0.5,0.5),取参数d1=8,m1=-5,δ=3,β=3,σ1=1.05,σ2= 0.01
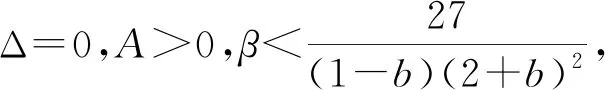

(a)随机模型 (b)确定性模型

(a)确定性模型

(b)随机模型
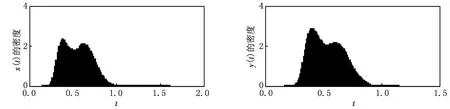
(c)密度函数

