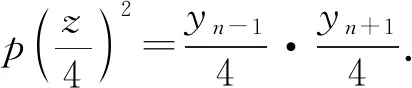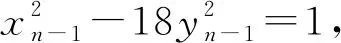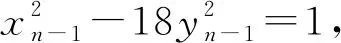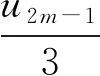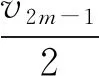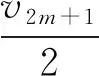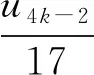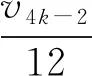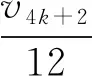关于不定方程组x2-18y2=1与y2-bz2=16的公解
瞿 云 云
(贵州师范大学数学科学学院,贵州 贵阳 550001)
1 主要结论
近年来,关于不定方程组x2-ay2=k与y2-bz2=l(a,b∈Z+,k,l∈Z)的公解问题一直受到人们关注.当(k,l)=(1,1)时,文献[1]证明了当a,b是不同的非零正整数时,x2-ay2=1与y2-bz2=1有至多3组正整数解(x,y,z);文献[2]证明了当a=4m(m+1),m,b∈Z+时,x2-ay2=1与y2-bz2=1至多有1组正整数解(x,y,z);文献[3]证明了当a=4m2-1,m,b∈Z+时,此方程组至多有1组正整数解(x,y,z);文献[4]得到了对于任意的素数p,x2-24y2=1与y2-pz2=1仅有正整数解(x,y,z,p)=(49,10,3,11),(485,99,70,2).当(k,l)=(1,4)时,文献[5]讨论了a=2,b=p或pq(p,q是不同的素数)的情形.当(k,l)=(1,16),a=18时,文献[6]讨论了b=2p1…ps(1≤s≤4),p1,…,ps是互异的奇素数的情形;文献[7]讨论了b=2n,n∈Z+的情形.本文讨论了b=p(p为任意素数)或b=pq(p 定理1若p为任意素数,则不定方程组 x2-18y2=1与y2-pz2=16 (1) 只有平凡整数解(x,y,z)=(±17,±4,0). 定理2若p,q(p x2-18y2=1与y2-pqz2=16 (2) 除开对于任意素数p,q有平凡整数解(x,y,z)=(±17,±4,0)外,有1组非平凡整数解(x,y,z)=(±19 601,±4 620,±136),此时p=2,q=577. 引理1[8]设k>1是一个整数且k≠169,除开k=2v2,v∈Z的情形,方程x2-(k2-1)y4=1有另一正整数解(x,y)=(8v4-1,2v)之外,此方程仅有正整数解(x,y)=(k,1). 引理2[9]设b,d>1都是非平方的整数,方程b2x4-dy2=1至多有1组正整数解(x,y). 引理4(1) 不定方程x2-332 928y4=1仅有正整数解(x,y)=(577,1); (2) 不定方程x2-288y4=1仅有正整数解(x,y)=(17,1); (3) 不定方程32X4-2Y2=1仅有正整数解(X,Y)=(1,2); (4) 不定方程X2-8Y4=1除开(X,Y)=(3,1)外,无其他正整数解; (5) 不定方程172X4-2Y2=1仅有正整数解(X,Y)=(1,12); (6) 不定方程X4-2Y2=1不存在正整数解. 证明(1) 332 928=5772-1,由引理1可知命题成立. (2) 288=172-1,由引理1可知命题成立. (3) 方程32X4-2Y2=1有1组正整数解(X,Y)=(1,2),由引理2可知命题成立. (4) 由文献[11]中引理可知命题成立. (5) 方程172X4-2Y2=1有1组正整数解(X,Y)=(1,12),由引理2可知命题成立. 其中:ε=γ2,η=δ2.则xn,yn,un,vn具有如下性质: (1)yn-1=17yn-4xn,yn+1=17yn+4xn,yn+2=577yn+136xn. (2)y2n≡0(mod136),y4n+1≡4(mod136),y4n-1≡132(mod136). (3) 当n是奇数时,(yn-1,yn+1)=136;当n是偶数时,(yn-1,yn+1)=4. (6)u2m-1≡0(mod3),v2m-1≡0(mod2),u4m-2≡0(mod17),v4m-2≡0(mod12),v4m≡0(mod204),m∈Z+. 证明Pell方程x2-18y2=1,x2-2y2=1的全部非负整数解为(xn,yn),(un,vn),n≥0,由数列xn,yn,un,vn的性质可得到性质(1)—(2),(6)—(7). (3) 当n是奇数时,令n=2k+1,则由性质(1)—(2)有 (yn-1,yn+1)=(y2k,y2k+2)=(y2k,577y2k+136x2k)=(y2k,136)=136; 当n是偶数时,令n=2k,则由性质(1)—(2)有 (yn-1,yn+1)=(y2k-1,y2k+1)=(y2k-1,577y2k-1+136x2k-1)=(y2k-1,136)=4. (5) 由于 定理1的证明Pell方程x2-18y2=1的全部非负整数解为(xn,yn),n≥0.设(xn,yn,z)为方程组(1)的非负整数解,由引理5性质(4)可知, (3) (4) 或 (5) 其中z=z1z2. (6) 或 (7) 其中z=z1z2. 定理2的证明Pell方程x2-18y2=1的全部非负整数解为(xn,yn),n≥0.设(xn,yn,z)为方程组(2)的非负整数解,由引理5性质(5)可知 (8) 情形1n为偶数.令n=2m,m>0,于是由引理5性质(6)及(8)式可得 (9) 情形2n为奇数.令n=2m+1,m≥0,于是由引理5性质(6)及(8)式可得 (10) 当m=0时,由(10)式可得方程组(2)的平凡整数解(x,y,z)=(±17,±4,0);当m>0时,对m分奇数与偶数两种情形进行讨论. 当m=2k-1,k≥1时,由(10)式得 (11) 当m=2k,k≥1时,由(10)式得 (12)2 若干引理
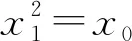
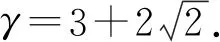


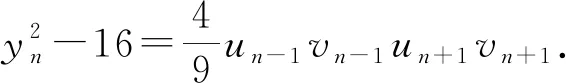
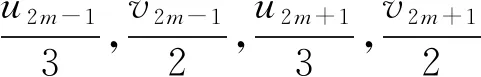

3 定理的证明