电磁测力系统研究

葛 锐 王小三 孙凤举 崔忠亮

(1.浙江省计量科学研究院，杭州310018；2.北京航天计量测试技术研究所，北京100076)

1 引 言

电磁测力系统是利用通电线圈在磁场中受力的原理进行测力的系统，广泛应用于电子天平、电磁天平中，用于完成测量点受力的测量。在工程应用中，电磁测力系统所测力值与通电线圈中的电流强度成正比，测量线圈中的电流强度可与电磁力大小建立联系。

德国Sartorius公司、瑞士METTLER TOLEDO公司的电磁测力系统产品已经商业化，分辨力达到0.1μg，处于国际领先水平，其研究内容属于技术秘密，较少见到相关报道。国内相关研究较少，仍处于原理性应用阶段。一般来说，国内电磁测力系统的测量范围在100g到10kg不等，分辨力在0.1mg到1g不等。

介绍一套电磁测力系统，该对磁感应强度和通电线圈的长度保持为常量的条件下进行研究，可以提高电磁测力系统准确度。

2 电磁测力系统

电磁测力系统基本构成主要由杠杆支点、杠杆横梁、永磁体构成的磁场及通电线圈组成的力矩器以及速度变换器、位移传感器、数采系统等组成[1]，如图1所示。电磁测力系统的测量原理为

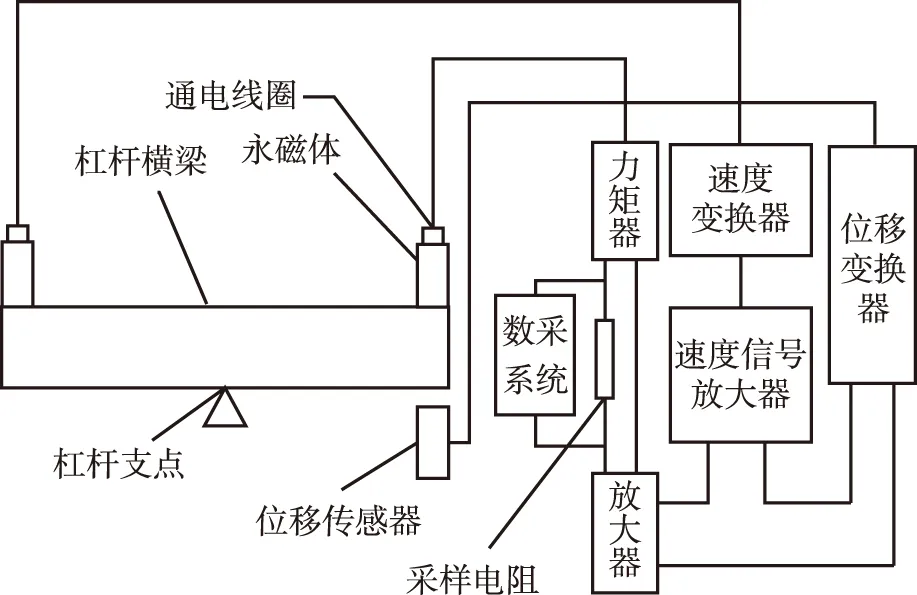
图1 电磁测力系统基本构成示意图Fig.1 Schematic diagram of electromagnetic force measuring system

F=BIL

(1)

式中：F──通电线圈在磁场中受力，N；B──磁感应强度，T；I──通电线圈中的电流强度，A；L──通电线圈的长度，m。

当有不平衡力作用在杠杆上时，杠杆绕支点旋转，位移传感器测量出杠杆横梁的偏转角度，输出电流，进入放大器。与此同时，横梁偏摆，在永磁体构成的磁场中，线圈切割磁力线，参数电流输出，该效应在原理图中体现为速度变换器，作为阻尼信号，速度变换器的输出电流经过放大后，与位移变换器的输出信号进行加和放大，电流反馈到作为力矩器的通电线圈中，该线圈在在永磁体组成的磁场中受力，与杠杆系统所受不平衡力矩相平衡。相关过程的控制方框图如图2所示，由控制方框图可知，当采样电阻阻值一定时，采样电阻上的电压降与质量成唯一对应关系。

图2 电磁测力系统控制方框图Fig.2 Control block diagram of electromagnetic force measuring system

3 永磁力矩器

3.1 永磁力矩器结构

永磁力矩器示意图如图3所示。图中，导磁体和永磁体一起形成磁路，通电线圈在磁路中受竖直方向的力。为保持通电线圈在磁路中所受的磁感应强度为常量，需对磁系统进行研究分析：一是永磁力矩器内磁感应强度的分布，二是通电线圈在磁场中的位置。

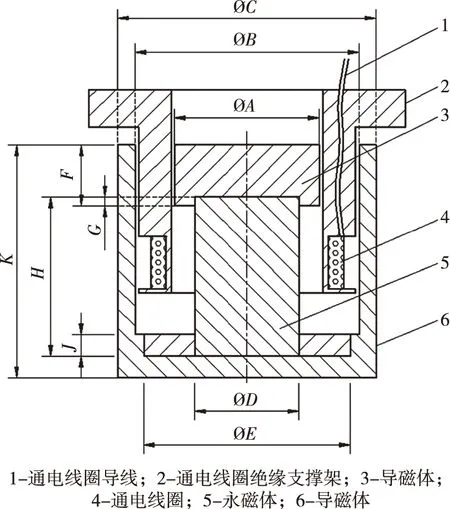
图3 永磁力矩器示意图Fig.3 Structure diagram of the permanent magnet torquer

3.2 磁系统

3.2.1磁系统基本参数

为了确保磁系统的磁感应强度的均匀性、稳定性满足要求，拟对多组结构进行分析，具体参数如表1所示。使用Maxwell 3D建立的永磁力矩器模型如图4所示，模型路径绘制如图5所示，模型路径是指为计算指定区域的磁感应强度分布，在计算之前绘制的一个考察路径。导磁体的BH曲线如图6所示。

表1 永磁力矩器结构参数Tab.1 Structureparametersofthepermanentmagnettorquermm尺寸代号第一组尺寸第二组尺寸第三组尺寸第四组尺寸A11173890B172652104C213060120D8.4123080E16.8244896F4.971428G0.7124H12.9518.53774J2.52.5510K18.92754108

图4 Maxwell 3D建立的永磁力矩器模型Fig.4 Permanent magnet torquer model established by Maxwell 3D

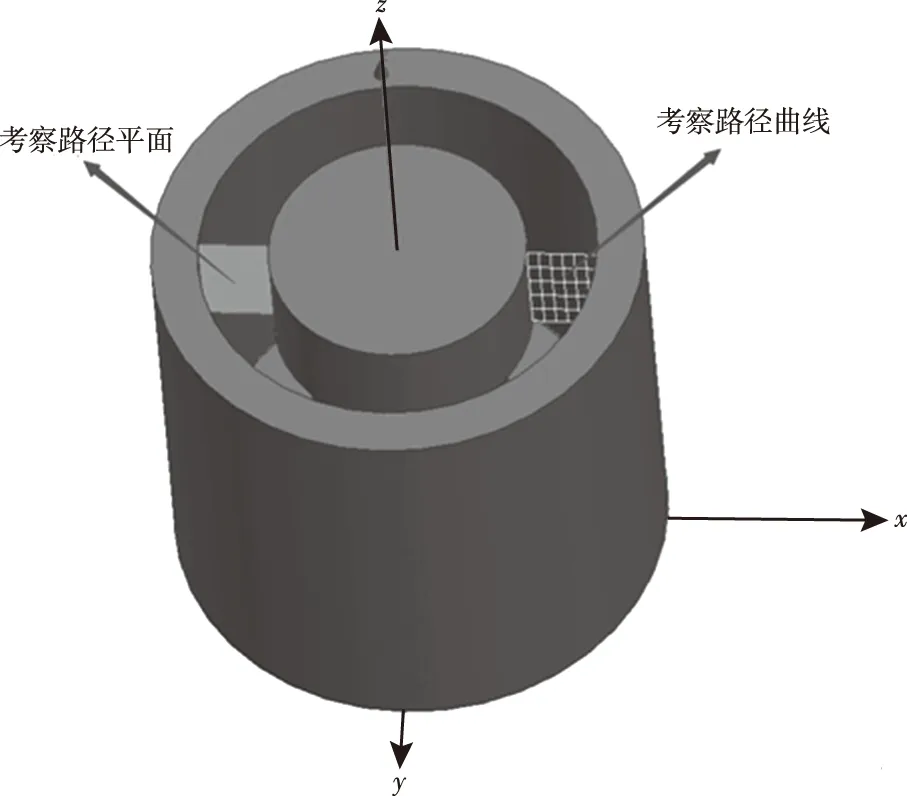
图5 绘制指定路径Fig.5 Draws the specified path

图6 导磁材料的BH曲线Fig.6 BH curve of the magnetic material

3.2.2三维静磁场分析

(1)三维静磁场分析结果

对表1给出的力矩器，使用Maxwell 3D工具，分别分析其模型磁密的模分布云图、模型剖面磁密的模分布云图和考察路径平面磁密分布图，第一组为结果如图7～图9所示，其余三组图略。

图7 模型磁密的模分布云图(第一组)Fig.7 Distribution cloud chart of the model magnetic density norm(group 1)

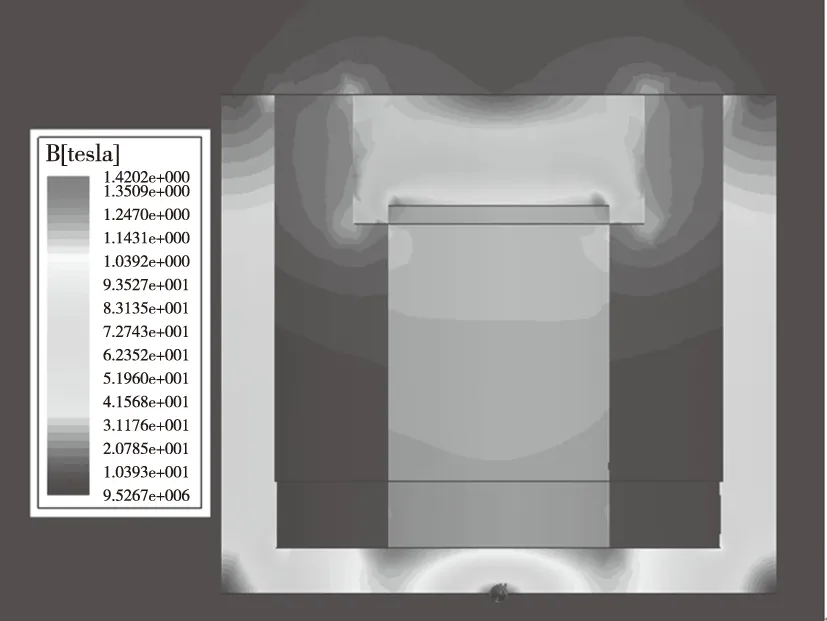
图8 模型剖面磁密的模分布云图(第一组)Fig.8 Distribution cloud chart of the model magnetic density norm on one section(group 1)

图9 考察路径平面磁密分布图(第一组)Fig.9 Distribution map of magnetic density on the plane of the studied path(group 1)

通过对以上四组不同尺寸的力矩器模型仿真分析，可以得出：力矩器的磁通在线圈工作的气隙中最集中。磁通尽可能沿磁阻小的磁路闭合。通过分析对比四组考察路径平面的磁场分布，第一组气隙磁场分布很不均匀，差异很大，大部分分布在(0.15～0.23)T。第二组的气隙磁场分布比较不均匀，差异比较大，大部分分布在(0.12～0.26)T。第三组的气隙磁场分布比较均匀，大部分分布在(0.18～0.28)T。第四组的气隙磁场分布比较均匀，大部分分布在(0.27～0.48)T。靠近工作气隙的地方出现饱和现象，且沿轴向气隙磁场分布比较不均匀。在平行于z轴的气隙两端磁感应强度呈现先减小再增大的趋势，在中间部分磁感应强度呈现先增大趋于稳定值，然后再减小的趋势。在平行于y轴的方向上，磁感应强度呈现逐渐均匀减小的趋势。力矩器磁路的几何参数决定着其磁场分布，它的外缘厚度影响着外部的漏磁大小，而足够大的磁钢环厚度保证了工作气隙有较高磁感应强度。

(2)三维静磁场优化改进

根据以上分析结论，结合电磁测力系统，对三维静磁场实施优化改进，改进完成后的实际尺寸如表2所示。

表2 优化后永磁力矩器结构参数Tab.2 Structuralparametersoftheoptimizedpermanentmagnettorqueconvertermm尺寸代号ABCDEFGHJK尺寸值385266304830237554

改造完成后，空气域磁感应强度的曲线在30mm内有一段变化量较小，相关设计工作可以在这一段内完成。相应的设计图3所示的通电线圈的尺寸大小可为15mm，即在用磁力矩器的5mm到22mm处，一边留1mm的余量，在这个范围内基本上磁感应强度由468mT到458mT之间线性变换。所以要保持磁感应强度为常量，只要通电线圈在永磁力矩器中的位置发生改变，事实上较难实现。为了满足理论模型，提高测量准确度，有两种途径：一是使通电线圈所处位置磁感应强度尽量均匀，二是使整个过程中通电线圈在用磁力矩器中的位置变化尽量少。

3.3 通电线圈在磁场中的位置控制

3.3.1测控系统

测控系统设计所考虑的核心问题是要完成极小力值的高准确度测量。为了确保极小力值的高准确度测量，从电磁力公式入手，考虑两方面问题：一是测量过程中，磁感应强度必须保持恒定，具体手段为尽力降低杠杆横梁的偏转角度，使通电线圈在磁场中的位置变化在可接受的范围内；二是在测量过程中，合理调整通电线圈长度，既要满足电流的测量需求，又要考虑横梁位置必然偏转，适度加大通电线圈长度，可对磁感应强度的变化产生平均效果，结合极小力值测量需求，小电流的准确测量为项目的不可避免的研究内容。测控系统设计总体思路如图10所示。

图10 测控系统设计总体思路Fig.10 Overall design idea of the measurement and control system

3.3.2控制系统

控制系统是具有负反馈线路的电磁补偿系统，主要由高隔离度电路、高闭环回路增益的放大、负反馈线路的电磁补偿以及电磁系统驱动电路组成。其控制原理是当存在力矩差时，杠杆横梁倾斜，位移变换器敏感该信号，经隔离电路和高增益放大后，通过驱动电路给力矩器提供驱动电流并使矩器产生力矩，使横梁反向倾斜，确保杠杆快速稳定。

若提高位移信号的增益，测量过程中，杠杆横梁的偏转角度将变小，对本项目具有非常积极的意义：可同时满足质量法干扰力矩消除技术中提出的两个基本条件；可使测量过程中，通电线圈在磁场中的位置保持恒定，提高模型准确度；通电线圈的长度可适度降低，提高系统中通电线圈中的电流强度，降低测量难度。

(1)高增益高稳定度电路

针对杠杆横梁偏转角度的控制要求，在控制系统中设计了高增益电路，系统闭环增益达到万倍，满量程时杠杆横梁的偏转角度由0.2865°降低为0.002°。

(2)分段微分自校准

测控系统的输入信号来自于位移变换器，将杠杆横梁倾斜的角度转换为位移(即弧长)后以电信号的方式输出给驱动电路，如图11所示。位移变换器的位移信号在全范围内并非线性，具有一定的弧度，因此在全范围内必须提升其线性。通过研究分段微分自校准技术，将位移信号在整个量程内划分为多个等距的极小弧度，通过微分原理，使得极短的弧线可视为直线，从而位移信号和电压信号便是线性转换关系，电压信号可以通过线性转换方程计算出位移信号。通过分段微分自校准，提升了电磁测力系统的线性度。

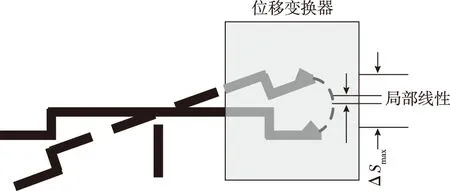
图11 分段微分工作原理示意图Fig.11 Schematic diagram of the segmented differential operation principle

4 试验结果对比

完成永磁力矩器研究后，其它配置保持不变，在1mg～10g范围内进行了测试[2]，将测量结果与采用最小二乘法拟合得到的不同加载时的理论值进行比较[3～5]，如表3所示。根据对比，本次研究效果良好。

表3 研究前后试验结果对比表Tab.3 Comparisonofthetestresultsbeforeandafterthestudy序号加载砝码值(g)偏转角度(°)示值(mV)最小二乘法拟合值(mV)拟合值与示值之差(mV)研究前研究后研究前研究后研究前研究后研究前研究后10.001//0.000100.000100.00121-0.000040.00111-0.0001420.005//0.000490.000500.001610.000360.00112-0.0001430.020.0001/0.002020.002000.00310.001860.00108-0.0001440.050.0021/0.004950.005000.00610.004860.00115-0.0001450.10.0032/0.010010.010000.011080.009870.00107-0.00013

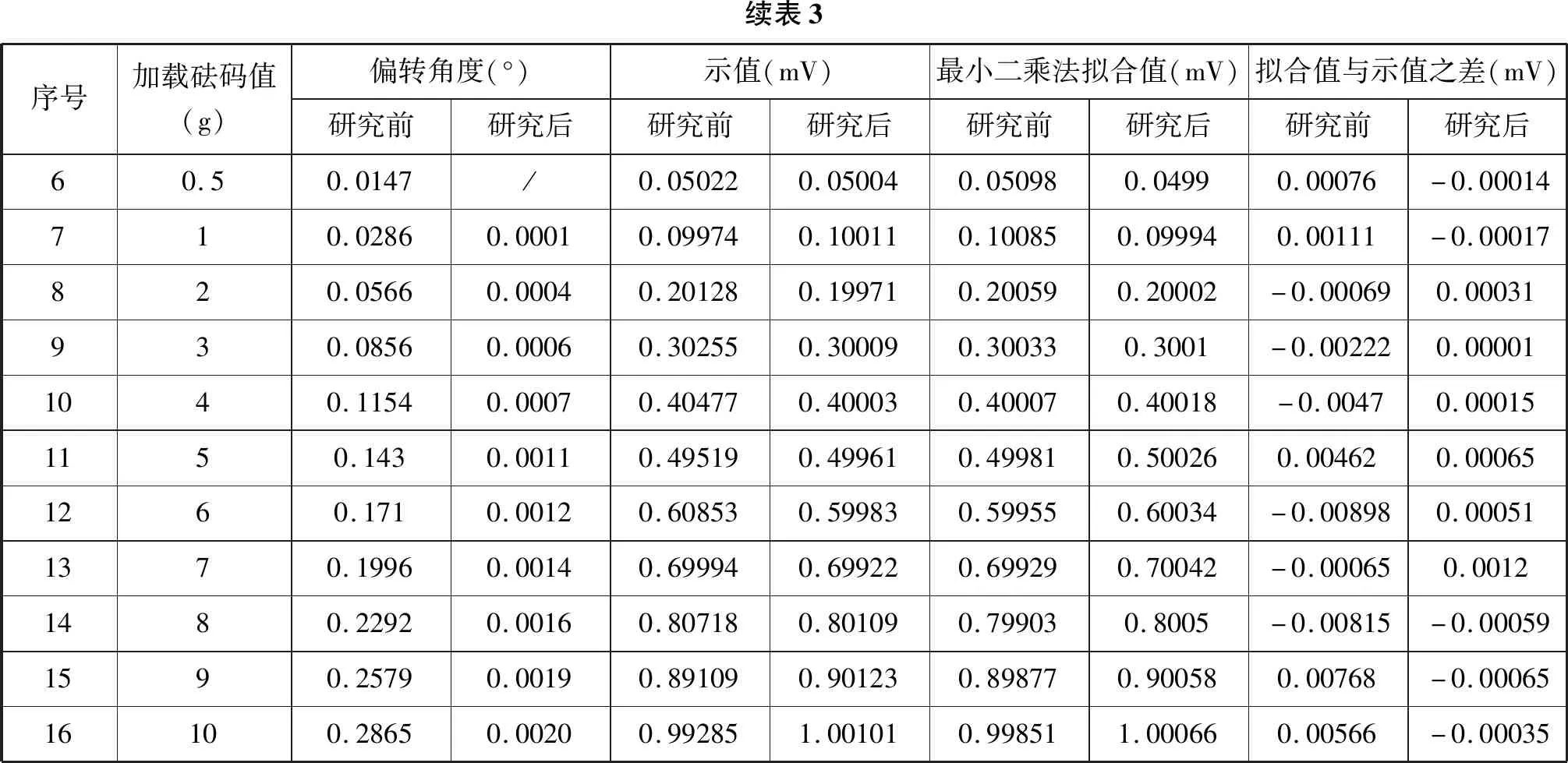
续表3序号加载砝码值(g)偏转角度(°)示值(mV)最小二乘法拟合值(mV)拟合值与示值之差(mV)研究前研究后研究前研究后研究前研究后研究前研究后60.50.0147/0.050220.050040.050980.04990.00076-0.00014710.02860.00010.099740.100110.100850.099940.00111-0.00017820.05660.00040.201280.199710.200590.20002-0.000690.00031930.08560.00060.302550.300090.300330.3001-0.002220.000011040.11540.00070.404770.400030.400070.40018-0.00470.000151150.1430.00110.495190.499610.499810.500260.004620.000651260.1710.00120.608530.599830.599550.60034-0.008980.000511370.19960.00140.699940.699220.699290.70042-0.000650.00121480.22920.00160.807180.801090.799030.8005-0.00815-0.000591590.25790.00190.891090.901230.898770.900580.00768-0.0006516100.28650.00200.992851.001010.998511.000660.00566-0.00035

5 结束语

本文对电磁测力系统进行了研究，主要以磁感应强度的分布、通电线圈在磁场中的位置控制为研究对象，通过优化磁系统结构改善磁路均匀性，优化测控电路减小通电线圈在磁路中位置改变等措施，降低了电磁测力系统的系统误差，使电磁测力系统的测量准确度有较大提高。下一步将集中在磁感应强度分布均匀性、通电线圈常量化以及通电线圈温升补偿等方面进行研究。