基于逆频响函数法的浅水域目标水下辐射声源级反演
刘玉财 陈 毅 易文胜 杨柳青
(杭州应用声学研究所,杭州 310023)
1 引 言
近几十年,随着经济的快速发展及科学技术的进步,人类对广袤海洋的探索、开发和利用逐渐增多,涉及海洋的新领域也越来越广。由此,将不可避免地给海洋环境造成各种各样的影响。目前,除水质污染、生态污染外,海洋人为噪声污染也是一个不容忽视的重要方面,其造成的相关危害也正逐渐加大[1~3],越发引起人们的关注[4]。此外,军用舰船以及水下无人运动平台自身辐射噪声强度也将对其声隐蔽性和水声设备性能造成影响,甚至危害其自身安全,如何准确有效地对辐射噪声进行定量评估就显得尤为重要[5,6]。
要减少大型振动结构件水下辐射噪声的危害及影响,须对振动声源加以研究控制[7]。准确测量噪声源强度成为噪声振动控制的一个重要手段,可为评估设备自身噪声及噪声治理效果提供基础数据[8]。目前,常用的声源强度测量方法有:时域分析法、频域分析法、波束形成法和声全息法等[9~11]。每种方法都可满足不同的需求。而我国近海海洋环境大部分为浅水域,测试的声学环境不满足理想自由场条件,往往存在多源、复杂反射及高背景干扰等问题,使得上述方法的应用受到限制[12]。
IFRF方法是基于信道的频率响应函数,通过构建的声传播模型建立起测量场点复声压与声源信号之间的关系,对声传递函数矩阵进行求逆来推算声源强度分布。P.A.Nelson和S.H.Yoon[13]对IFRF方法在近场声源成像方面的性能做了理论分析,并在实验室空气环境下证实了该方法的有效性,为近场测量反演声源强度提供了理论指导。由于求逆的频响逆矩阵函数常常是病态的,会产生不适定问题。为此,S.H.Yoon和P.A.Nelson[14]引入Tikhonov正则化法和截断奇异值法来改善病态传递矩阵在求逆过程中的畸变,有效提高了重建声源强度的准确性,不过会使得IFRF方法重构结果具有有限的空间分辨率。在随后的时间里,Q.Leclere、A.Derouiche 和N.Hamzaoui等[15~19]人相继研究并发展了IFRF方法反演理论。
IFRF方法反演声源强度具有较高的准确性,目前对该算法的研究还不够完善,大多数都是集中在空气消声室或是消声水池的自由场环境下,而在实际工程测量所遇到的声学环境大都是非自由场。由于该算法具有不受声学系统限制的特点,本文对IFRF方法应用于浅水域水下目标声源级反演的可行性和有效性进行了探索,结合射线理论的虚源法构建水下目标辐射声场计算模型,给出了IFRF方法反演的基本过程,仿真分析了噪声等关联因素与IFRF反演算法准确性的关系,最后通过水池和湖上试验对本文所提算法的准确性进行了验证测试。
2 基本原理与算法
2.1 虚源法原理
虚源法基于射线声学理论,将有界水域辐射总声场视为点源和一系列虚源辐射声波叠加干涉的总和,每个虚源对声场的贡献遵循球面波传播规律,各虚源的声源强度应由界面反射系数及反射次数进行加权[20]。根据《GJB 4057-2000舰船噪声测量方法》[21]对测试的规定,在近距离测试及测试时间较短时,可忽略水体介质的声吸收,并且认为水体密度、声速保持不变。因此,对均匀浅水域单点声源辐射声场进行建模,不失一般性,选取水平向右为x轴正向,竖直向下为z轴正向,如图1所示。

图1 声场计算模型Fig.1 Sound field calculation model
考虑深度为H的浅水域环境,G点为声场中任意接收点,目标声源Q01坐标为(0,Z01)。为匹配水底界面反射特性,应附加一个与声源Q01相对水底对称的虚源Q02,设为第一个虚源,为使满足水面处的边界条件,同样在海面附加Q01和Q02分别关于水面对称的虚源Q03和Q04,将此四个声源记为零阶声源。零阶四个声源相对水面水底分别又有对称虚源,如此反复,建立无限多个虚源,即构成有限水域声场计算模型。令
(1)
式中:Rlζ——虚源Qlζ与测量点的距离;L——点声源与测量点间水平距离;H——水体深度;l——虚源阶数;ZS——点声源深度;ZR——测量点深度。
略去时间因子,依据声波叠加原理,点声源辐射空间声场中任意点处的声压信号为
(2)
式中:j——虚数;k——波数;Wi1,Wi2——分别为第i阶虚源中第1条、第2条声线的水底反射系数;V——水面反射系数,假定为-1。
第l阶虚源第ζ条声线的入射角为
(3)
水底反射系数遵循瑞利反射模型为[22]
(4)
式中:Wiζ——第i阶虚源中第ζ条声线的水底反射系数;m——沉积物密度与水介质密度的比值;n——水介质和沉积物介质中声速的比值。
2.2 基于逆频响函数的反演算法
频响函数建立起了测量场点复声压与声源强度之间的关系,通过对频响函数矩阵进行求逆[23]处理,就可从辐射声场测量中反演得到声源强度值。空间声场中任何位置测量到的声压在时域上可以表示为
p(hG,t)=psignal(hG,t)+pnoise(hG,t)=
H(hS,hG,t)×q(hS,t)+pnoise(hG,t)
(5)
式中:p(hG,t)——深度hG处测量点G接收到的时域声压信号;psignal(hG,t)——测量接收到的时域目标信号;pnoise(hG,t)——测量时的干扰噪声;H(hS,hG,t)——声源S至测量点G的信道响应函数;q(hS,t)——深度hS处的声源时域信号强度。
为便于分析,可通过快速傅里叶变换将时域信号转化到频域上
p(hG,ω)=H(hS,hG)q(hS,ω)+pnoise(hG,ω)
(6)
式中:p(hG,ω)——深度hG处接收时域信号的傅里叶变换;H(hS,hG)——声源S至测量点G的信道频响函数;q(hS,ω)——深度hS处声源的频响函数;pnoise(hG,ω)——深度hG处测量点接收噪声的频响函数。
考虑在空间声场中存在N个声源,并选取M个测量接收点进行声场信号的采集,从声源到测量接收点的声传播问题可以表示为
(7)
将公式(7)表示为矩阵向量形式
PM×1=HM×NQN×1+Pnoise=Psignal+Pnoise
(8)
式中:PM×1——测量场点复声压向量;HM×N——复频响应函数矩阵;QN×1——声源强度向量;Psignal——测量场点信号声压向量;Pnoise——测量场点噪声声压向量。

(9)
将公式(9)用矩阵向量形式重新表示为
(10)
式中:Qreal——实际声源强度向量;Qbias——反演声源强度误差向量。

当M>N时,无法直接对矩阵HM×N求逆,求解公式(10)为超定问题。可以利用矩阵广义逆来求解
(11)

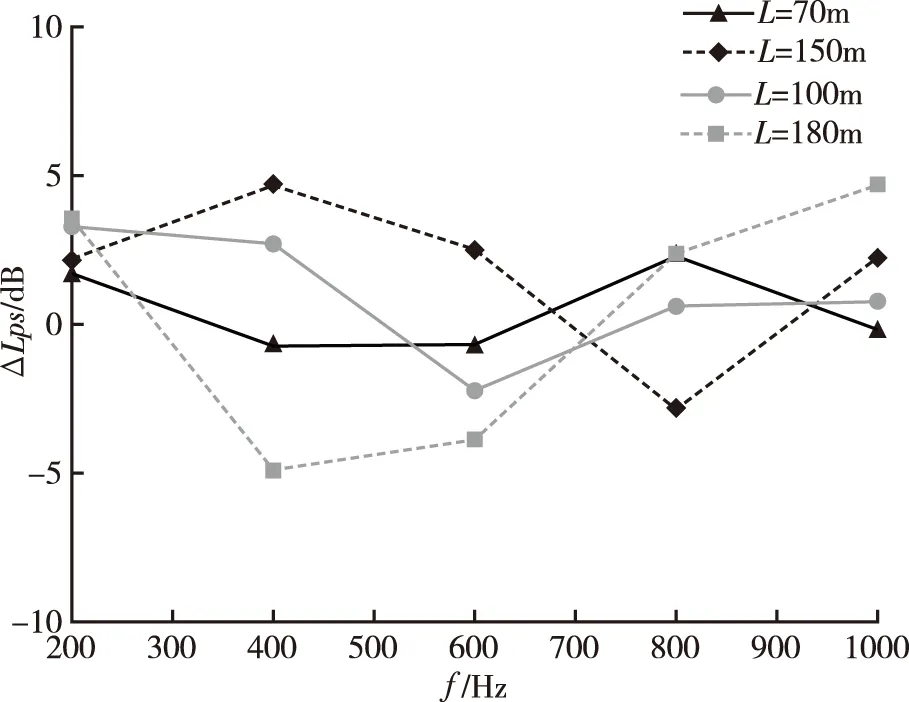
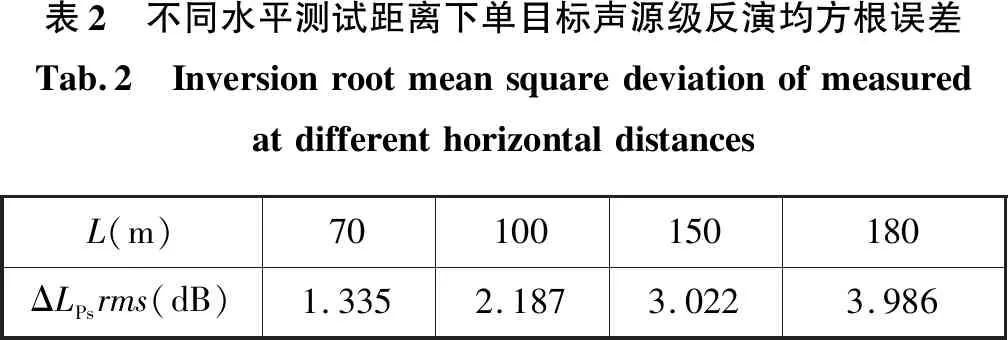
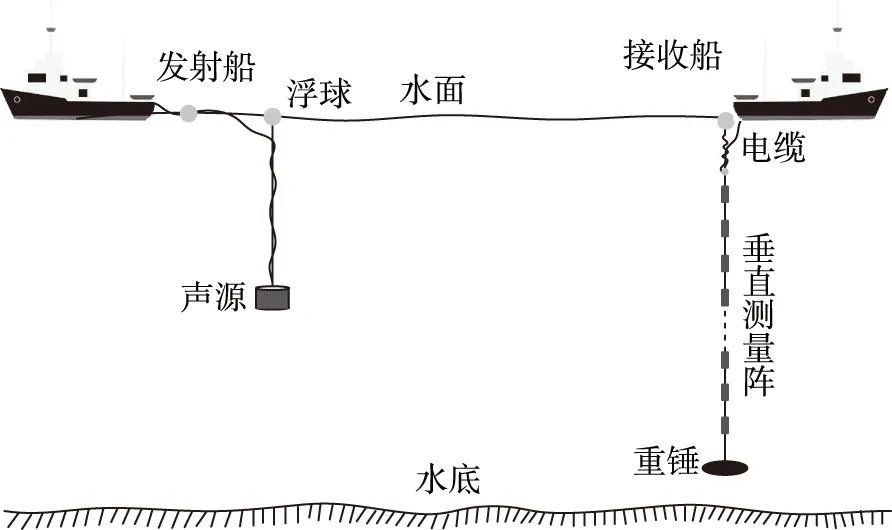
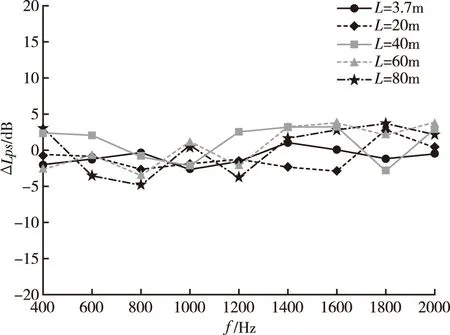
当M (12) 逆频响函数法反演声源强度的原理可用图形化表示,如图2所示。 图2 逆频响函数方法原理Fig.2 Schematic of inverse frequency response function method 从实际测量角度出发,典型外场测量环境通常为浅海、天然湖泊或大型水库,测试对象有单目标或多目标,在此假定测试对象可视为点声源,并采用垂直线阵进行声场测量,测量声阵位置需满足目标辐射声场远场条件。 2.3.1单目标声源 浅水域环境单点声源辐射空间声场任意位置声压可以看做不同虚源辐射声波的叠加,令 qlζ=κlζ·q01 (13) 式中:qlζ——第l阶虚源中第ζ号声源的声源强度;κlζ——声源强度系数;q01——实际点声源的声源强度。 将公式(2)重新表述成下列形式 (14) 式中:pnoise——测量场点噪声声压。 将公式(7)展开成下列形式 (15) 式中:τ——测量声压序号。 2.3.2多目标声源 水下多目标声源的空间辐射声场是多个点声源及其对应虚源辐射声波叠加干涉的结果,可将多目标辐射声场中某点处的声压描述为 p=pnoise+ (16) 式中:qγ——第γ号声源的声源强度。 为便于分析,将公式(16)表示为 p=[H1…HN][q1…qN]T+pnoise (17) 仿真选取均匀浅水域环境,以单目标为测试对象,在计算获得的声压信号中添加高斯白噪声来模拟获得带噪声的接收信号,其余部分仿真参数为:声场模型虚源阶数选取8阶,设定水深65m,水平测试距离100m,点声源深度15m,采用32元等间距垂直线阵进行测量,阵元间距2m,信号频率为(200~2000)Hz。得到声源强度反演误差随频率和信噪比的变化关系如图3所示。 图3 反演误差随信噪比和频率的变化Fig.3 Variation of inversion error with SNR and frequency 为便于直观对比分析,选取的信噪比为3dB和6dB时的反演误差对比曲线如图4所示。测试频带内对于不同信噪比下反演误差的均方根值如图5所示。 图4 不同信噪比对应反演误差曲线Fig.4 Inversion deviation under different SNR 图5 不同信噪比对应频带内反演均方根误差Fig.5 Inversion root mean square deviation in frequency bands under different SNR 分析图3及图4中的曲线,可以看出,在(200~2000)Hz频段内,不同信噪比所对应的声源级反演误差随频率呈现无规律起伏波动变化;在信噪比较低时,部分频点处的误差将高于3dB,随着信噪比的提高,这种情况得到明显改善。结合图5统计数据分析,在整个测试频段内,随着信噪比的提高,反演误差逐渐减小,并趋于稳定,并且在较低信噪比下,仍具有较好的测试精度。 浅水域环境声源辐射空间声场呈现出明显起伏分布特征,测量深度及测点个数不同,获取的声场信息将存在较大差异,并直接影响IFRF方法中频响函数矩阵的特性。为准确分析不同声场测量点数单一变量对IFRF方法反演目标辐射声源级的影响。设定信噪比为20dB,采用不同阵元个数的等间距垂直线阵对空间垂向声场进行测量,同时保证阵列最上方水听器深度相同,测量阵位置满足目标声场远场测试条件,入水深度2m,水平测试距离50m,其余仿真条件不变,仿真结果如图6所示。不同声场测试点数下声源强度反演误差的均方根值如表1所示。 图6 不同测试点数对应声源强度反演误差Fig.6 Inversion deviation under different sound field test points 表1 不同场点测试点数下的声源强度反演均方根误差Tab.1 InversionrootmeansquaredeviationunderdifferentsoundfieldtestpointsdBN161820242832ΔLPsrms1.0930.3780.2600.2360.1950.149 对比分析图6曲线及表1给出的统计值,可知,在(200~2000)Hz测试频段内,随着声场测量点数的增多,反演得到的声源级误差曲线起伏逐渐减弱,反演均方根误差相应呈现下降趋势。当测试点数大于24时,随着测试点数的增加,测试频带内的反演误差减小不明显,这是由测试信号中带有噪声引起的测量误误差。当测试点数小于18时,有部分频率处的误差开始增大,超出合理范围,并逐渐在低频段出现大的畸变。经分析,该现象是由频响函数矩阵特性引起的,声场测量点数的减小会导致频响函数矩阵条件数的增大,低频辐射声场分布特点会使得阵列测试信号相关性增大,导致频响函数矩阵出现大的奇异值,这种病态矩阵将给目标声源级反演带来较大影响。 为验证IFRF方法的合理性和仿真结果的准确性,分别在波导水池和外场湖泊两种声学环境下进行了测试试验。受波导水池尺寸限制,为模拟声源在实际浅水域环境下的声场特征,采用缩比测量方式,提高测试信号频率;在湖上测试时,直接采用低频声源辐射低频声信号进行试验。 为验证IFRF方法反演单目标声源级在不同参数条件下的准确性,试验选择在杭州应用声学研究所的波导水池进行,水池参数及测试系统示意图如图7所示。水池四周铺设有橡胶吸声尖劈,采用的标准声源和测量水听器型号分别为杭州应用声学研究所自研的RHS-20和RHC-10,等间距垂直测量阵包含12个阵元,阵元间距0.1m,线阵最上方水听器入水深度0.1m,标准声源入水深度0.6m。根据水深与频率的对应关系,在(10~50)kHz频段内选取部分频率信号进行测试,信号形式为连续波,垂直线阵水平测量距离满足换能器辐射声场为远场的测试条件。在对试验数据进行处理时,测试参数已换算为实际环境对应参数表示,图8和表2给出了不同水平测试距离下声源级反演误差变化,图9和表3给出了不同声场测试点数下声源级反演误差变化情况。 图7 波导水池及试验布置示意图Fig.7 Waveguide pool and test layout diagram 图8 不同水平测试距离下单目标声源级反演误差Fig.8 Inversion deviation of measured at different horizontal distances 表2 不同水平测试距离下单目标声源级反演均方根误差Tab.2 InversionrootmeansquaredeviationofmeasuredatdifferenthorizontaldistancesL(m)70100150180ΔLPsrms(dB)1.3352.1873.0223.986 图9 不同测试场点个数下单目标声源级反演误差Fig.9 Inversion deviation of measured at different sound field test points 表3 不同测试场点个数下单目标声源级反演均方根误差Tab.3 InversionrootmeansquaredeviationatdifferentsoundfieldtestpointsdBN681012ΔLPsrms3.7333.1282.8381.835 从图8中可以看出,实测信号反演误差随频率呈现无规律的起伏变化,结合表2中不同测试工况下反演均方根误差值可知,在近距离范围内,IFRF方法反演声源强度具有较高的精度,随着测试距离的增大,反演得到的声源强度误差增大。对图9及表3中的数据分析可知,声场测试点数选取对反演误差具有较大的影响,测试点数的增多,可以明显改善方法反演性能。在本试验中,测试点数约在10个以上,可以保证结果的准确性。通过上述两组参量分析,可以看出,试验结果与仿真结果具有很好的一致性,验证了IFRF方法反演单目标声源级的可行性。 通过水池试验验证IFRF方法反演双目标声源级的性能,试验选用两个一致性较好的RHS-20型发射换能器作为声源,声源垂向布置,间距为0.3m,上方声源入水深度0.5m,上下声源分别记为1#和2#目标,得到不同水平测试距离下双目标声源级反演误差变化如图10所示。 图10 不同水平距离下双目标声源级反演误差Fig.10 Inversion deviation of double target sound source level at different horizontal distances 从图10中可以看出,采用IFRF方法能够较好的反演出两个目标各自的声源级值。在整个测试频段内,随着水平测试距离的增大,IFRF方法反演双目标声源级的误差会开始增大,这是由于声波随距离的增长存在扩展,同一水池深度、不同水平距离处的声信号强度量值不同,造成不同水平距离下声阵测试信噪比不相等而引起的。 测试采用IFRF方法反演目标声源强度在实际环境下的可行性和准确性,同时与水池试验结果进行相互验证。试验于某湖上水声试验中心进行,采用船载移动测试方式,试验测试示意图如图11所示。测试水域底部平坦,平均水深约为45.6m,水面平静,采用16元等间距垂直线阵,阵元间距1m,声阵覆盖水下(4~19)m范围深度,低频声源入水深度5m,测试频率范围为(400~2000)Hz,信号形式为连续波。图12和图13分别给出了不同水平测试距离的对应目标声源级反演误差曲线及测试频带内反演误差统计值。 图11 湖上试验测试示意图Fig.11 Schematic diagram of lake test 图12 不同水平测试距离下声源级反演误差Fig.12 Inversion deviation of sound source level at different horizontal distances 图13 不同水平距离对应频带内反演均方根误差Fig.13 Inversion root mean square deviation infrequency bands under different horizontal distances 从图12可以看出,水平测试距离的增加,在测试频段内,部分频点处的误差超过3dB,起伏也较大,但整体误差都在合理范围内。结合图13的统计数据可知,在近距离测试条件下,偏差随距离的增加是缓慢增长的。主要由两方面因素引起:一是距离的增大使得测试信号信噪比减小,以及声传播信道的影响增大。综合上述两次试验数据分析,两次试验数据具有很好的一致性并且与理论仿真分析结果相符合,有效验证了本文IFRF方法反演水下目标辐射声源级的可行性和准确性。 本文提出了一种采用IFRF方法反演浅水域目标水下辐射声源级的方法,从理论和试验上对该方法的可行性和准确性进行了推理验证。与传统球面波衰减法及波束形成法推算相比,逆频响函数法将各边界面反射信号作为有效输入,同时考虑了声信道及声场起伏的影响。对虚源法声场计算理论以及IFRF反演方法的原理进行了推导描述,应用于浅水域水下目标辐射声源级反演计算建模,给出了场点声压与源点信号强度之间的函数关系。选取单点声源为目标,模拟分析了IFRF方法反演声源级的效果。最后,在波导水池和湖上分别进行了验证试验,分析不同测试状况下的声源级反演效果。仿真及试验结果表明,本方法对浅水域环境目标水下辐射声源级的反演是准确可行的。在后续的工作中,将进一步研究该方法在宽带连续信号及非均匀浅水域环境等情况下的实际应用效果。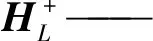

2.3 声场模型
3 数值仿真研究
3.1 背景噪声对声源级反演的影响



3.2 声场测试点数对声源级反演的影响


4 验证试验及结果分析
4.1 波导水池环境下单目标声源级反演试验



4.2 波导水池环境下双目标声源级反演试验

4.3 典型外场环境下单目标声源级反演试验

5 结束语

