管道有源噪声控制中壁面分布次级声源的空间分布优化

罗平展 张芳杰 徐健 李晓东†

(1 中国科学院噪声与振动重点实验室(声学研究所)北京 100190）

(2 中国科学院大学北京 100049）

0 引言

有源噪声控制技术已成功应用于管道中的低频噪声控制。相比于控制管道中的平面波，高阶模式声波的控制要求更高，是有源控制的难点问题[1]。由于控制高阶模式声波需要多个换能器，其中一个难点是设计次级声源和误差传声器等换能器在管道中的空间布放。已有文献对控制管道中的高阶模式声波进行了一些探索，但是换能器的最优空间分布尚未得到阐明[2-3]。考虑到实际应用中诸如风洞和地铁等大型通风管道，为了保障畅通，要求换能器分布在管道侧壁[4-5]。因此，本文主要研究次级声源在被约束于管道壁面条件下的空间分布优化问题。

管道中次级声源常被布放于管道截面。由于高阶模式主要由管道截面特性所决定，当次级声源合理分布在截面时，能有效控制各高阶模式声波。理论上使用N个次级声源最多可以控制前N个模式声波，即工作频率上限逼近第N+1阶模式声波的截止频率[2]。已有的研究工作表明，次级声源布放在管道截面时能够有效控制工作频率范围内的高阶模式声波，阻碍其通过截面传播至管道下游，从而得到优异的全局控制效果[3,6-7]。这种位于截面的布放方式应用广泛，对于在管道和腔体等出口处抑制噪声辐射同样有效[8]。因此，将次级声源布放在管道截面上成为有源噪声控制中的常见方案。

然而在部分应用中，由于实际条件限制使得次级声源被约束在管道壁面。此时噪声控制效果相比于次级声源位于管道截面时通常有所劣化，表现出降噪量下降且工作频率范围显著低于理论最优值等现象，更加凸显了优化设计管道壁面上次级声源空间分布的重要性[9]。已有研究工作针对壁面分布次级声源的空间分布优化问题的研究尚不充分。Stell等[2]指出次级声源的布放应当避开高阶模式声波的节线，以保证次级声源能较好地激励高阶模式声波。Zander等[10]针对2个次级声源的简单情形讨论了轴向间距的选择。Laugesen[11]考虑到在刚性壁假设下所有高阶模式声波在管道角落都能取到最大值，建议将次级声源布放在管道角落处以提高控制效率。在仿真实验中他还发现将次级声源沿管道轴向展开，可以增加系统控制的鲁棒性。Zhang等[12]对比了次级声源与误差传声器的径向分布，发现当次级声源和误差传声器的数量较少时，在相对的平行壁面上布放它们可以更好地控制高阶模式声波。但是这些研究工作由于缺乏详细的理论分析，没有得到系统性的完整结论，难以成为次级声源空间分布优化设计的具体指导准则。迄今为止，次级声源被约束在管道壁面时对于控制高阶模式声波的局限性，以及优化设计次级声源空间分布的原理和方法均未得到清晰彻底的解释。

针对管道中高阶模式声波的有源控制问题，本文研究了次级声源在管道壁面的空间分布优化问题。本文首先介绍了管道中次级声源激励高阶模式声波的理论模型；然后显式推导了次级声源空间分布对控制性能的影响，分析了次级声源空间分布的优化准则；最后在最优控制策略下，通过数值仿真，验证了次级声源空间分布优化准则的有效性。

1 理论模型

1.1 管道中次级声源激励高阶模式声波建模

不失一般性，假设一无限长刚性壁面的矩形管道，其截面为S=Lx×Ly。次级声源被约束在管道壁面，如图1所示。建立直角坐标系，约定z轴方向为管道轴向，xy方向为管道周向。将次级声源根据其振速分布建模为W(r′)，其中r′=(x′,y′,z′)表示声源位置。矩形管道中的格林函数为G(r|r′)，其中r=(x,y,z)表示观测点位置。为了表述简便，在下文的推导中省去时间项eiωt。

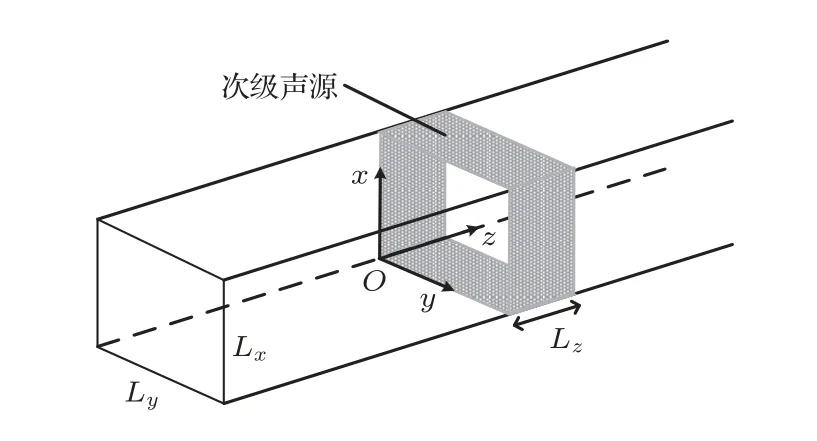
图1 壁面分布次级声源示意图Fig.1 The sketch of the boundary-located secondary sources

管道中次级声源所激励声场声压根据格林函数可以表示成[13]

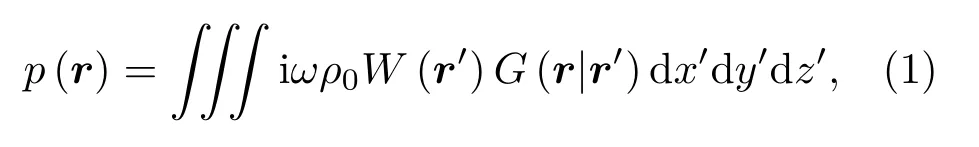
其中，ω为激励频率，ρ0为空气密度，格林函数G(r|r′)可以表示为

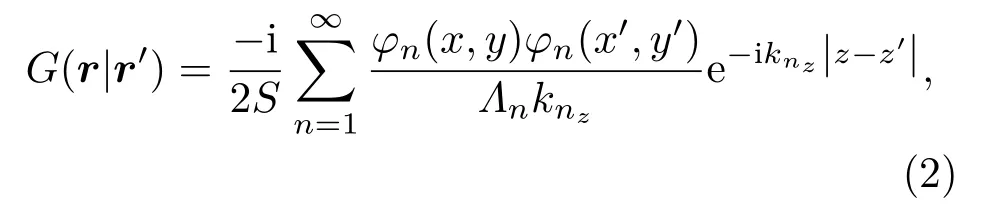
其中，φn表示管道的高阶模式声波。对于四周为刚性壁面的矩形管道，φn满足

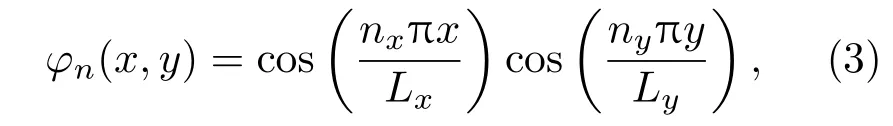
对应的归一化系数为

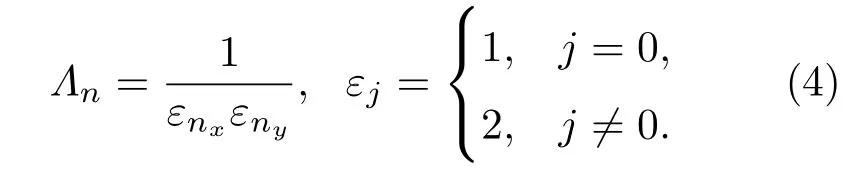
第n阶模式声波的波数k在各方向上的分量可以分别表示为

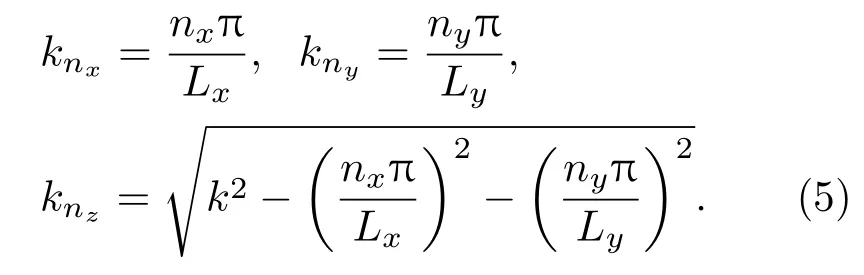
下文开始讨论壁面分布次级声源的空间分布对控制管道高阶模式声波的影响。假设次级声源的分布范围限于0≤z≤Lz范围内的4个壁面。构造次级声源分布Wm(r′)满足

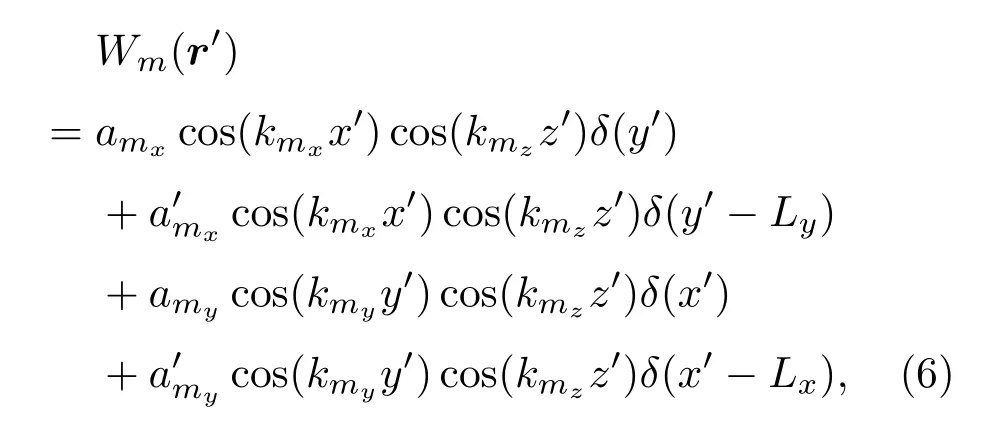
其中，δ()表示狄拉克函数的定义与式(4)中相同，即等于第m阶模式声波各方向上的波数。显而易见，Wm(r′)代表了在管道壁面上空间频率与第m阶模式声波的频率相同的4个面声源分别是这4个面声源的强度。根据傅里叶变换的原理，壁面上任意有限的次级声源的空间分布均能表示成不同Wm(r′)的叠加[14]。因此，通过研究Wm(r′)代表的次级声源分布对高阶模式声波的激励机制，可以推演得到任意有限分布的次级声源对高阶模式声波的激励。

不失一般性，只考虑向管道下游传播的高阶模式声波，管道内的声场可以分解成模式声波叠加的形式[13]，即

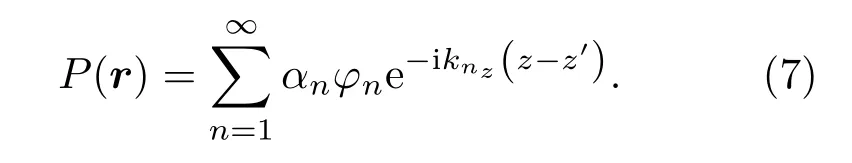
次级声源Wm(r′)在管道中所激励的高阶模式声波，可以通过将式(6)代入式(1)中得到，对比式(7)，得到Wm(r′)所激励的各阶模式声波的系数为

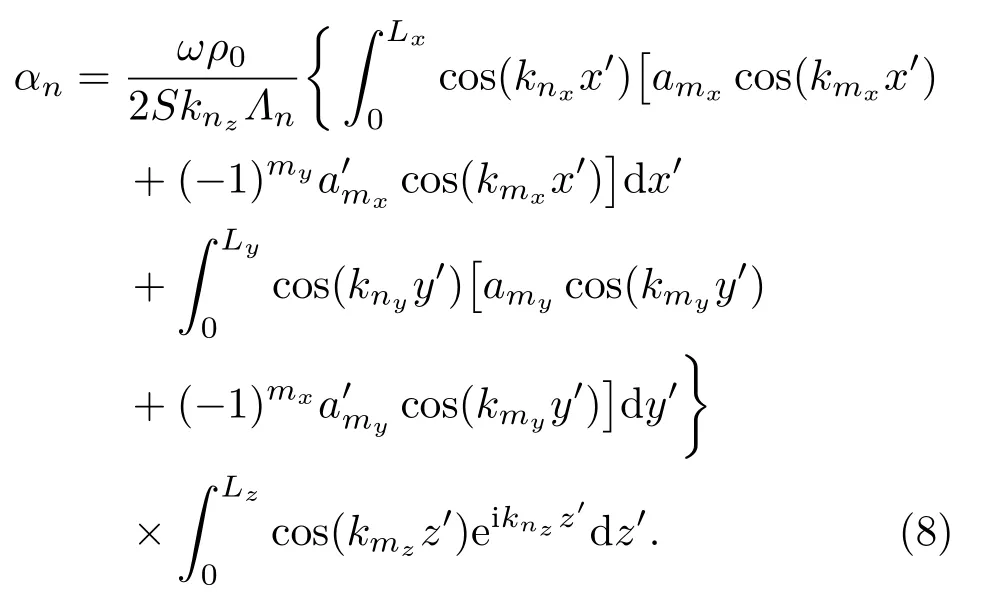
式(8)中包含了x、y和z三个方向的积分，彼此独立，分别计算如下。

首先，次级声源在x方向空间分布对于激励高阶模式声波的贡献可以写成

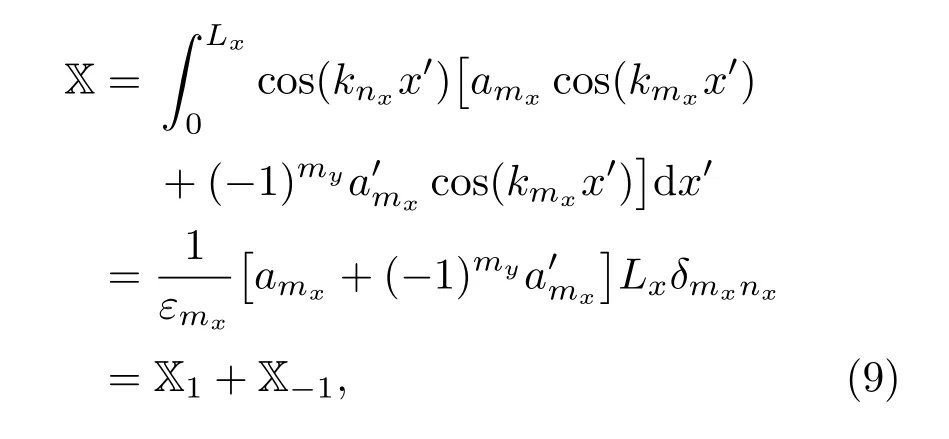
其中，δmn为克罗内克函数，它的值仅当m=n为1，其他时候均为0。式(9)中x方向的积分表明，在x方向按分布的次级声源，只激励mx相关的高阶模式声波，不会对其他模式声波产生影响。同时，管道中x方向上两个相对的平行墙面上次级声源的贡献分别为X1和X-1。可以令，则对于my为奇数的模式声波，X1和X-1反向，X为0，此时只激励my为偶数的模式声波；同理，可以令，此时只激励my为奇数的模式声波。这可以解释为，两个沿x方向沿伸的平行墙面等同于y方向的两点空间采样，可以控制my相关的两个模态，使得根据my的奇偶性可以区分和独立控制相关模式声波。

同理可得次级声源在y方向的空间分布对于激励高阶模式声波的贡献为

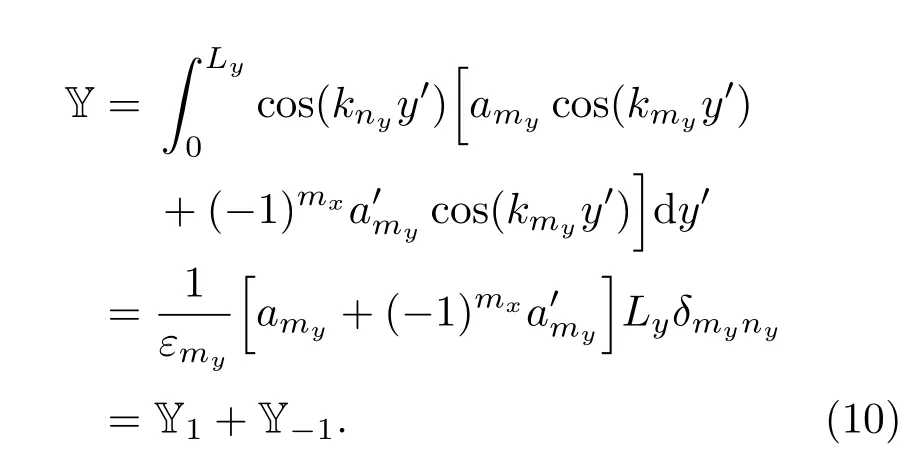
式(10)中y方向的积分表明，在y方向按kmy分布的次级声源，只激励my相关的高阶模式声波，不会对其他模式声波产生影响。同时，可以通过选择amx和a′mx的符号来决定Y1和Y-1的值，以选择性的激励mx相关的奇数阶或偶数阶模式声波。

最后，次级声源在z方向的空间分布对于激励高阶模式声波的贡献可以写成

其中，sinc(x)=sinx/x。式(11)表明壁面分布次级声源无法对z方向上的模式声波进行严格的独立控制，必然会激励各种高阶模式声波，这是壁面分布次级声源控制高阶模式声波局限性的体现。但是应注意到，式(11)中关于Lz/2只有一个线性项，其他均为随Lz的震荡衰减的sinc函数。因此，当Lz增大时，线性项增大从而显著大于其他sinc函数，使得在z方向上按照kmz分布的次级声源在轴向的尺寸Lz较大时能显著激励z方向上波数为kmz的模式声波。进一步考虑到，当x＞π时，有sinc(x)≪1，因此一般要求壁面分布次级声源的轴向尺寸Lz＞2π/min(knz-kmz)，其中min()表示在各种nz和mz的组合中选择波数差的最小值。

将式(9)、式(10)和式(11)代入式(8)，得到壁面分布次级声源激励的高阶模式声波可以写成

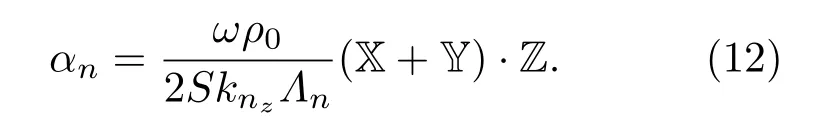
式(12)表明，壁面分布次级声源在x方向和y方向，即在管道周向的空间分布对激励高阶模式声波的贡献会直接线性相加，再与z方向即管道轴向上空间分布的贡献相乘，共同激励高阶模式声波。当次级声源在管道壁面上按照Wm(r′)分布时，主要激励第m阶模式声波；同理，第m阶模式声波也主要由Wm(r′)分布的次级声源激励。次级声源的空间分布频率和激励高级模式声波存在对应关系，是对高阶模式独立控制的理论依据。为了形象展示壁面分布次级声源在各方向上的空间分布对于控制高阶模式声波的贡献，图2给出了X、Y和Z对激励第m阶(mx,my)模式声波的贡献示意图，其中第m阶模式声波的幅度被归一化到1以方便比较。图2表明，壁面分布次级声源的空间分布对其控制性能非常重要。当次级声源在合理优化空间分布后能近似独立地控制管道中各高阶模式声波，从而实现较好的控制效果；但是若未被合理的布放，在激励目标模式声波时也将同时激励其他模式声波，无法实现独立激励各高阶模式声波，从而丧失对高阶模式的控制效果。

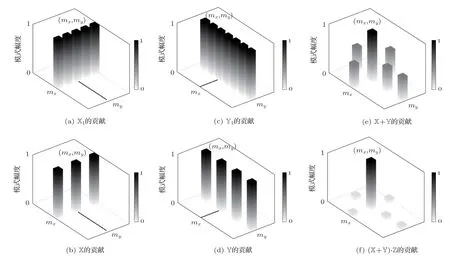
图2 壁面分布次级声源Wm(r′)激励(mx,my)模式声波的示意图Fig.2 Illustration of the mechanism of generating the(mx,my)mode by boundary-located secondary sources Wm(r′)

1.2 点声源控制策略

在实际应用中，常以扬声器作为有源控制系统的次级声源。由于其尺寸相对声波波长较小，此时次级声源应被建模成点声源。点声源可以看作声源连续分布W(r′)的空间采样，因此在满足采样定律的条件下前文所得关于次级声源空间分布的结论同样适用。次级声源最优驱动强度可以通过以最小化管道中声能流为目标的全局控制策略得到。本小节介绍控制策略的推导，以便后文对比次级声源空间分布对控制效果的影响。

为了表述方便，定义管道中的N个传播模式声波为a=[a1,a2,···,aN]T，M个次级点声源的驱动强度为q=[q1,q2,···,qM]T，对应的空间位置为对式(8)在上述位置进行空间采样，受激模式声波与次级声源的关系可以用矩阵的形式来表示：

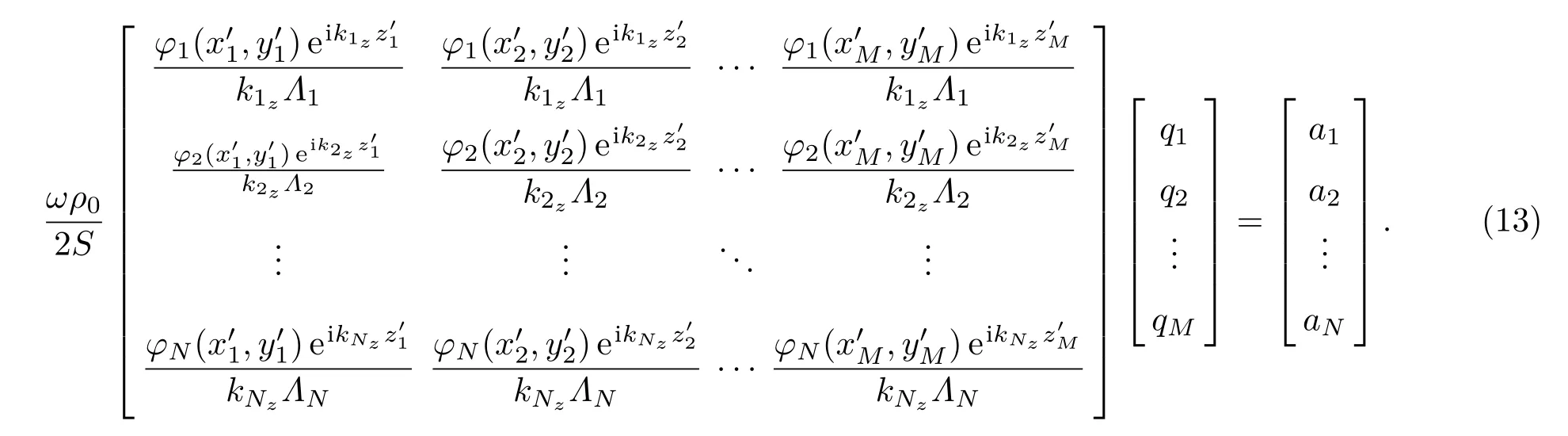
定义N×M维阻抗矩阵Ω(r′)，其各元素为

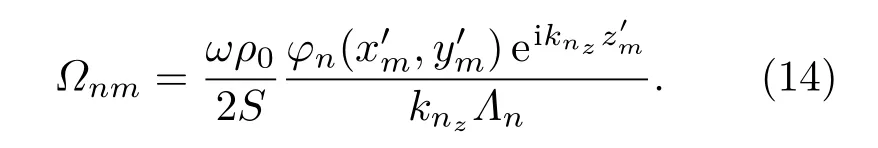
根据式(14)的定义，将式(13)重写为

下面讨论以最小化管道中声能流为目标的全局控制策略以及次级声源最优驱动强度的求解[3]。管道中声能流可以表示为

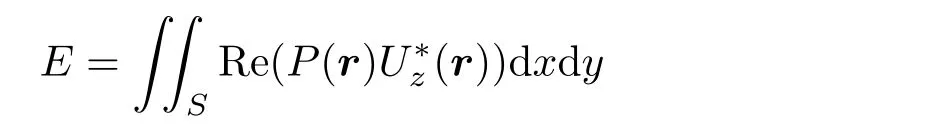
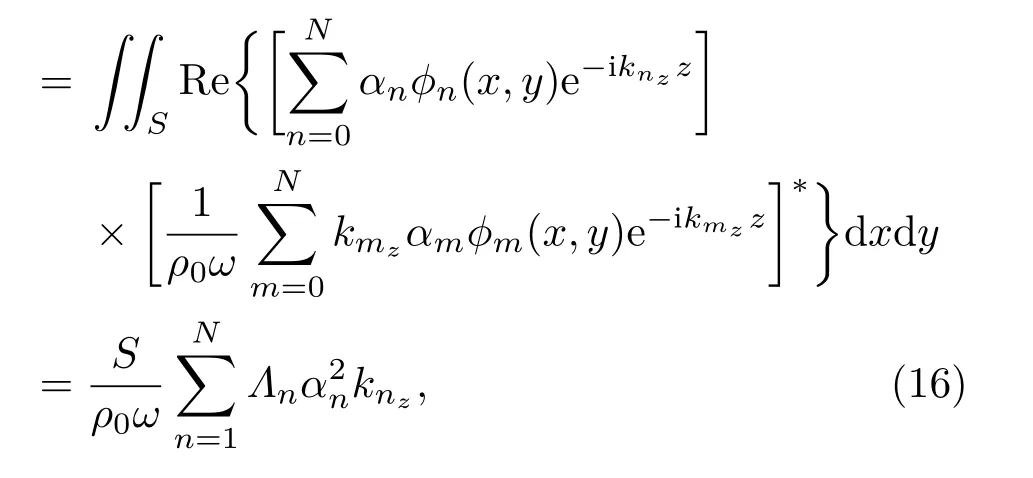
其中，Re()表示取复数的实数部分，Uz(r)是声场在z方向上的粒子振速，*表示共轭。注意只有传播模式声波能传递声能流。

定义一个N×N的对角矩阵，表示为

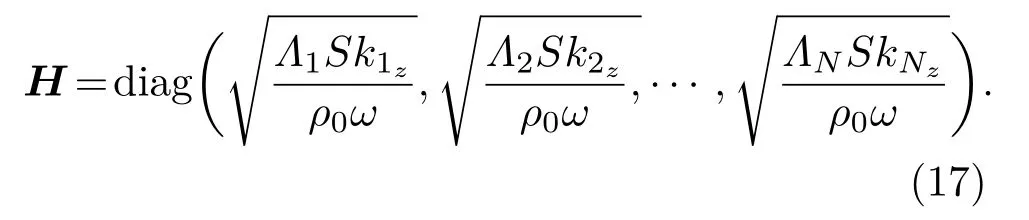
因此，式(16)中的声能流可以写成

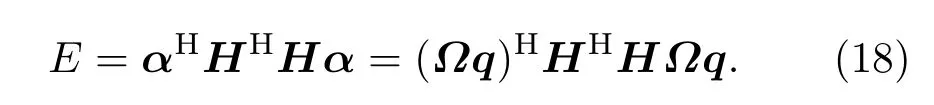
选用下标p和s分别表示与初级声源和次级声源相关的参量。初级声源的驱动强度、阻抗矩阵和激励的模式声波分别记作qp、Ωp和ap；同理，次级声源的驱动强度、阻抗矩阵和激励的模式声波分别记作qs、Ωs和αs。选择代价函数J为管道中初级声源和次级声源共同激励的总声能流与表示次级声源强度的惩罚项之和[2]，写成

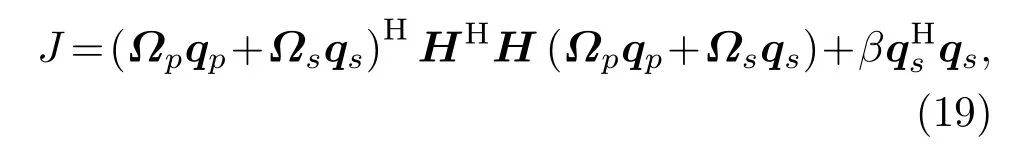
其中，β为正实数，用来限制次级声源的驱动强度大小[15]。取代价函数J对qs的导数为零，可得最优次级声源驱动强度qopt为

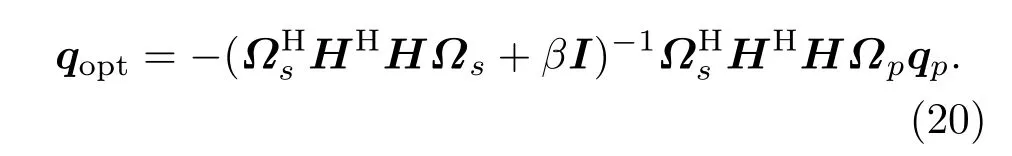
2 仿真实验与分析

下文通过数值仿真对比壁面分布次级声源在前文所述控制策略下的各种空间分布对高阶模式控制效果的影响，以验证本文所提出的理论模型和结论的有效性。

仿真实验中无限长矩形管道的截面积设为4.0 m×3.0 m(Lx×Ly)。管道中初级声场由布放在(0.0,0.0,-10.0)m处的点声源所激励，仿真中声波的频率范围设为30～210 Hz。在这个频率范围内，最多存在18个传播模式声波，对应的截止频率为fn=c/2[(nx/Lx)2+(ny/Ly)2]1/2。它们的阶数和截止频率的具体取值如表1所示。

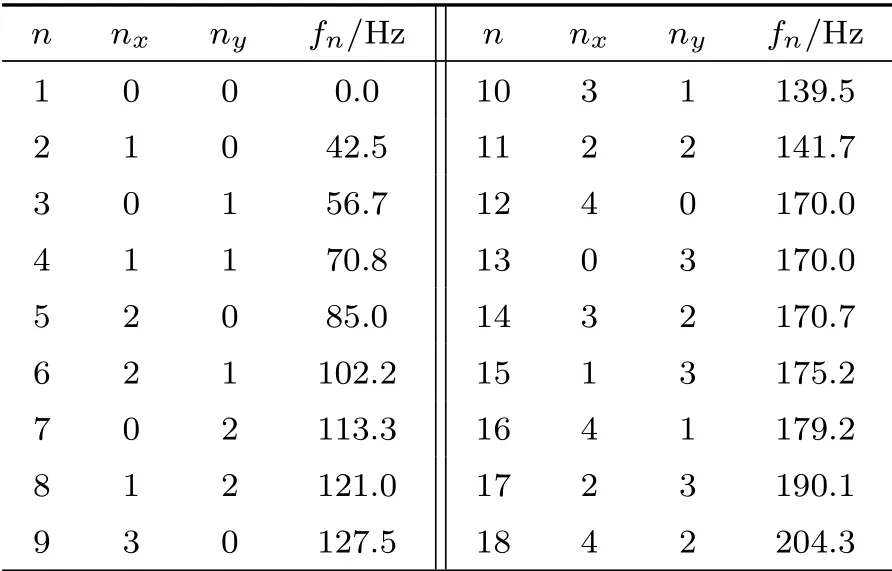
表1 管道中各阶模式声波的截止频率Table 1 The higher-order modes in the duct and the corresponding cut-on frequencies

对于前18阶模式声波，其阶数满足nx≤4和ny≤3，即在x方向上不超过5个模式声波，在y方向上不超过4个模式声波。因此根据采样定律，在x方向上和y方向上分别需要5个和4个次级声源。在z方向上对于可能的多层分布次级声源，其层间距和轴向尺寸分别记为ΔLz和Lz。为了方便比较，壁面分布次级声源在各方向上都服从均匀分布。仿真中β始终设为矩阵最大特征值的1/1000以保证矩阵求逆鲁棒性。为了与前文所述最小化管道声能流的控制策略一致，本文采用管道中残余的声能流作为控制效果的评价标准，并将得到的声能流做归一化处理，其中0 dB对应1.0×10-12W。

图3给出了x和y方向上壁面分布次级声源的空间分布示意图和相应的控制效果。其中，空间分布(1)～(4)分别对应前文中的X1、X、Y1和Y，即图2(a)～图2(d)。图3所示的结果表明，在低频段高阶模式声波数目相对较少时，各种空间分布的次级声源均能取得较好的控制效果。这是因为在这些频率范围内壁面分布次级声源对所有高阶模式声波均能实现独立控制，从而取得了接近最优的控制效果。但是，图3所示的壁面分布次级声源对高阶模式控制效果存在明显的工作频率上限。例如，对于图3中的次级声源空间分布(1)，其工作频率上限为56.7 Hz，对应第3阶(0,1)模式声波的截止频率。这是因为当频率低于56.7 Hz时，管道中仅有第1阶(0,0)和第2阶(1,0)模式声波。空间分布(1)为一个x方向上的线阵，可以独立控制不同nx的模式声波。当频率高于56.7 Hz时管道中出现了第3阶(0,1)模式声波，而空间分布(1)所示的次级声源无法独立控制(0,0)和(0,1)两个nx=0的简并模式，导致控制效果显著下降。而对于空间分布(2)，通过增加了一个x方向上的线阵，使得其可以独立控制ny相关的两个模式，因此可以同时控制(0,0)和(0,1)模式声波，相应的工作频率上限为(0,2)模式声波的截止频率113.3 Hz。此时空间分布(2)对应的次级声源无法同时独立控制(0,0)、(0,1)和(0,2)这3个nx=0的简并模式。同理可以解释空间分布(3)的工作频率上限为42.5 Hz是因为无法独立控制(0,0)和(1,0)模式，而空间分布(4)的工作频率上限为85.0 Hz是因为无法独立控制(0,0)、(1,0)和(2,0)三个简并模式。

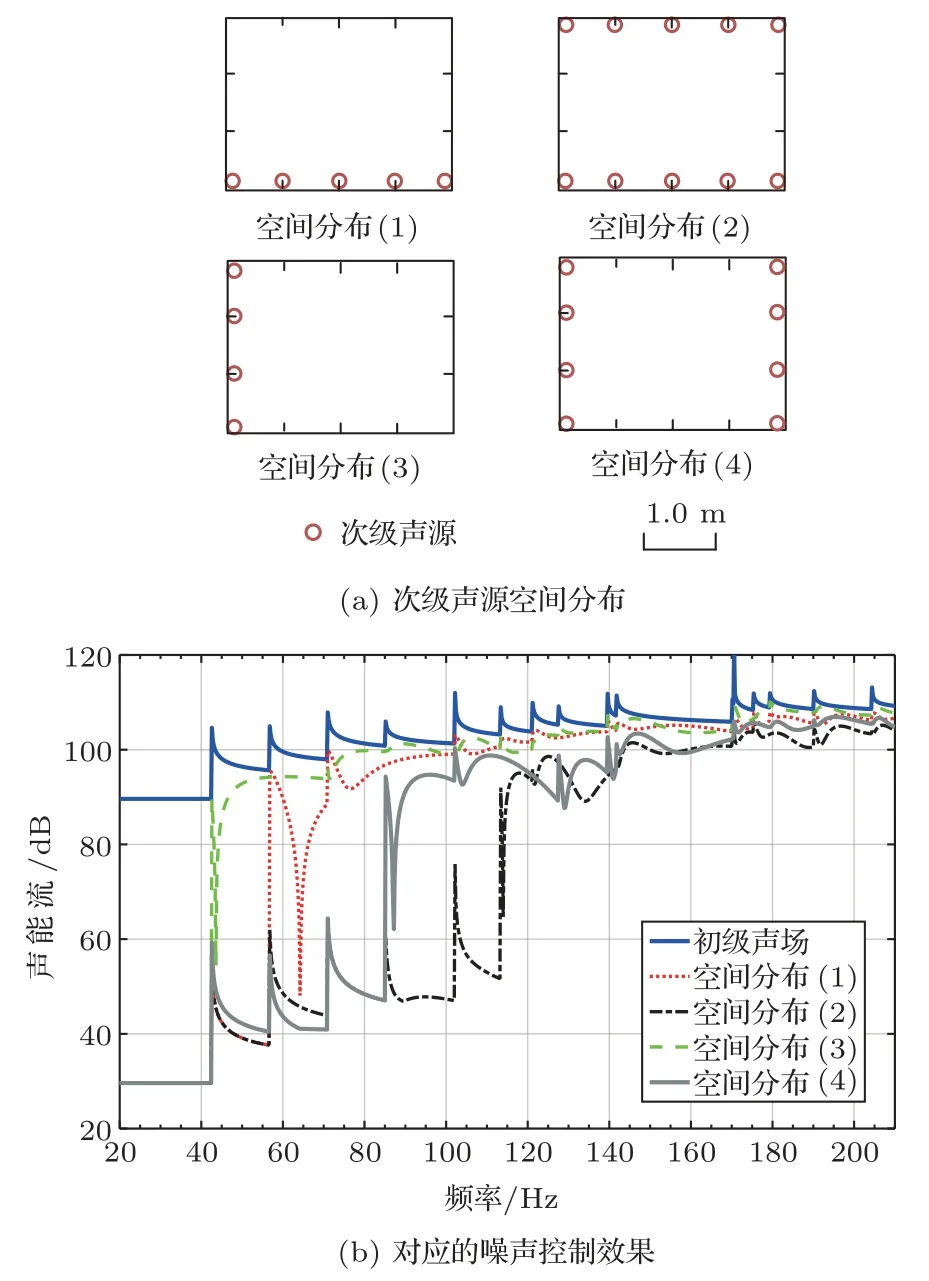
图3 壁面分布次级声源的空间分布与对应的噪声控制效果Fig.3 The spatial distribution and the corresponding control performances of the boundary-located secondary sources

图4给出了管道中单层和多层壁面分布次级声源的空间分布示意图和相应的控制效果。其中，空间分布(1)和空间分布(2)分别对应前文的X+Y和(X+Y)·Z，即对应了图2(e)和图2(f)。通过将x方向上和y方向上组合起来的单层壁面分布次级声源，对高阶模式声波的控制效果更好。此时，其工作频率的上限提升至141.7 Hz，对应第11阶(2,2)模式声波的截止频率，因为(2,2)模式声波在x和y方向上均有3个简并模式而单层壁面分布次级声源无法同时控制这些简并模式。通过在z方向增加一层次级声源，构成轴向间距ΔLz=1 m的双层分布，相比于单层分布的次级声源能够在高于141.7 Hz以上的频段取得20 dB以上的降噪量提升。该结果表明，次级声源沿着管道轴向分布时能更好地控制高阶模式声波，在频率相对较高和高阶模式声波数目较多时对于控制效果的改进更为明显。

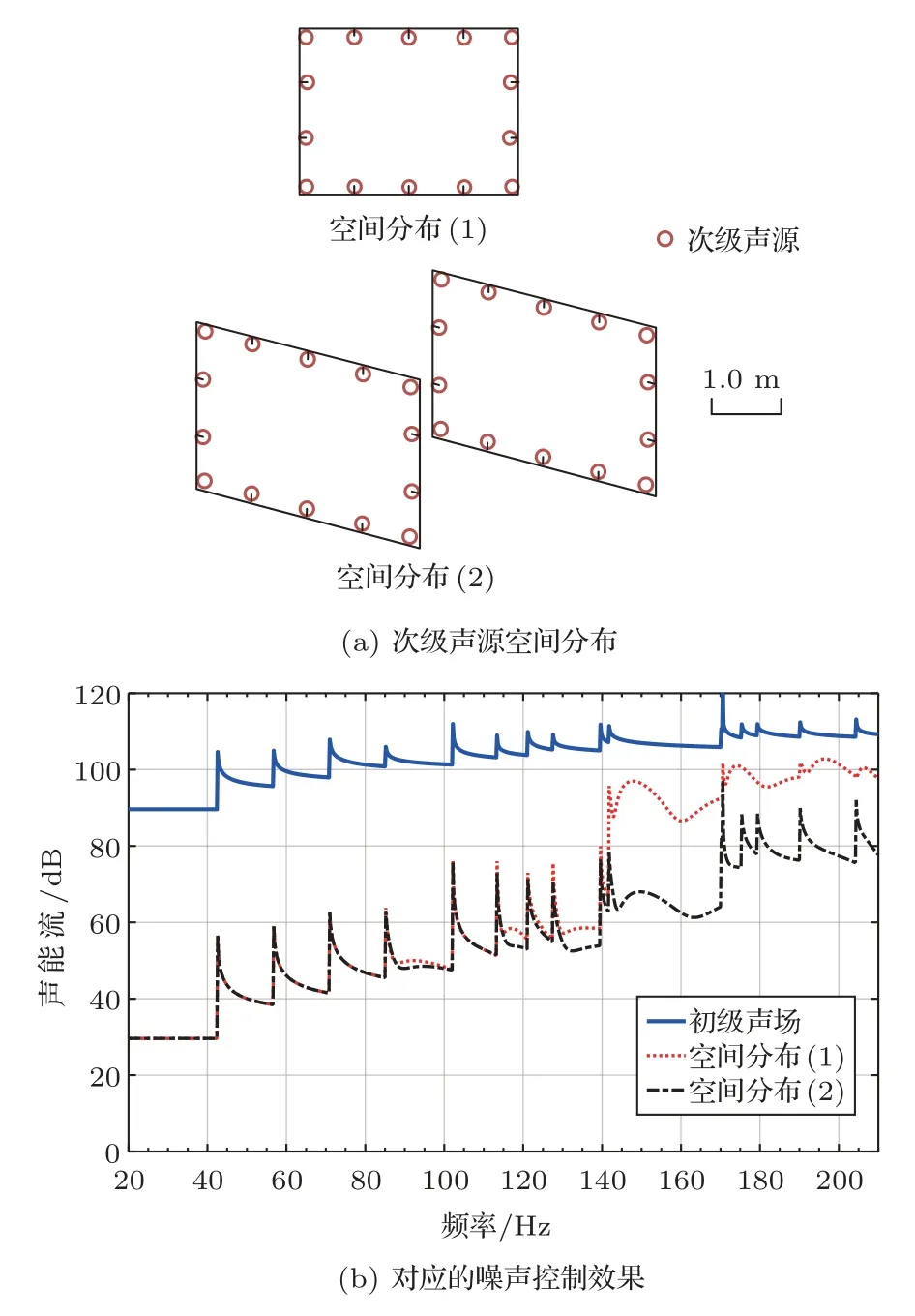
图4 壁面分布次级声源的空间分布与对应的噪声控制效果Fig.4 The spatial distribution and the corresponding control performances of the boundary-located secondary sources

进一步研究壁面分布次级声源的数量和间距对高阶模式声波控制效果的影响。首先讨论次级声源在管道周向上数目的影响。图5中展示了管道周向上6个、14个和22个壁面分布单层次级声源以及对应的控制效果。相比于周向上14个次级声源，周向上仅有6个次级声源时其工作频率上限降至113.3 Hz，对应着(0,2)模式声波的截止频率。这是因为此时次级声源在y方向上仅有2个次级声源，根据空间采样定律只能独立控制ny=0和ny=1两类模式声波，当频率超过113.3 Hz后(0,2)模式声波开始在管道传播时，壁面分布次级声源将失去控制效果。但是，次级声源在管道周向上的数目增加至22个并没有提升控制效果。根据采样定律这是因为22个次级声源属于过采样，不能改善控制效果。

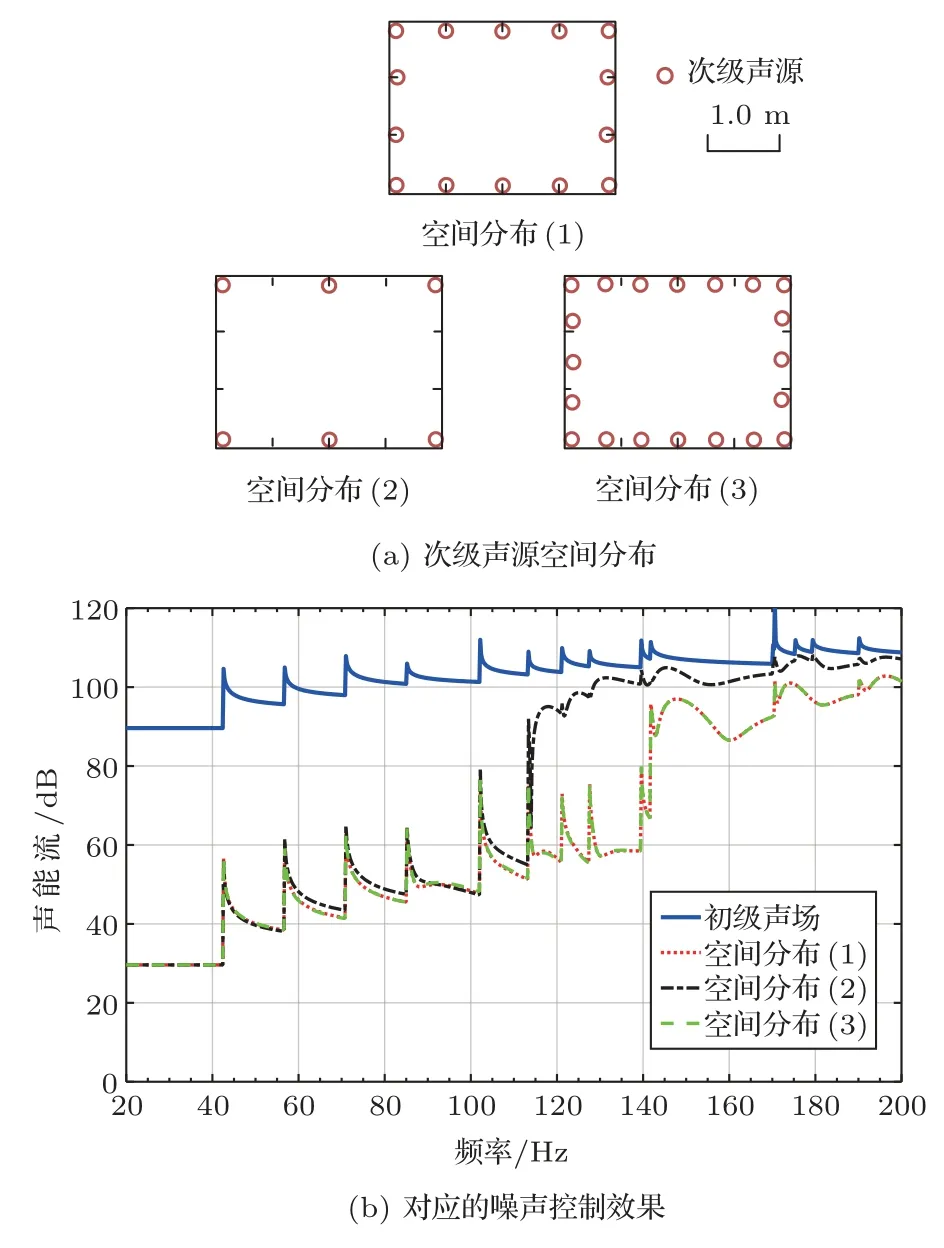
图5 壁面分布次级声源的周向上次级声源数量对控制效果的影响Fig.5 The influence of the number of the single-layer boundary-located secondary sources in the circumferential direction on the control performance

接下来研究次级声源在管道轴向上的数目和间距的影响。将壁面分布次级声源在周向上固定分布为14个，即按照图5(a)中空间分布(1)，层间距固定为ΔLz=1 m，轴向上不同层数的次级声源对高阶模式的控制效果如图6所示。图6中14×2表示在管道周向上有14个次级声源，在轴向上共有2层，其余表述以此类推。图6的结果表明，通过增加壁面分布次级声源在管道轴向上的层数，扩大次级声源在管道轴向上的分布范围，能进一步提高控制效果，尤其在相对高频段，高阶模式声波数目较多时控制效果提升更为明显。当次级声源的层数超过6层时，即轴向尺寸Lz超过5 m，壁面分布次级声源对高阶模式声波的控制效果达到接近最优，实现近60 dB的降噪量。

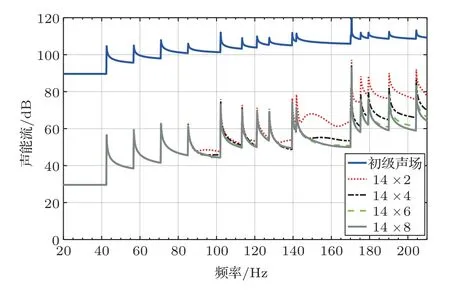
图6 轴向上不同层数的壁面分布次级声源对高阶模式控制效果Fig.6 The control performances achieved by different layers of boundary-located secondary sources

最后讨论壁面分布次级声源的轴向间距对控制效果的影响。本文提出的理论模型表明次级声源分布的轴向尺寸较大时有利于对控制高阶高阶模式，因此通过使用双层分布次级声源并增加层间距也能起到增大轴向尺寸的效果。壁面分布的14×2双层次级声源不同轴向间距对高阶模式声波的控制效果如图7所示。图7的结果表明，采样壁面分布双层次级声源并适当增大轴向间距同样能够获得较好的控制效果，尤其在相对中高频段增大轴向间距可以显著提高控制效果。但应该注意到在轴向间距很大时可能在部分频段出现降噪量下降的现象，例如对于轴向间距ΔLz=5 m相对于ΔLz=2 m在140 Hz左右对高阶模式的控制效果反而出现了恶化。这主要是轴向间距过大导致在轴向上不满足采样定律，使得控制效果恶化。尽管如此，总体来看采用壁面分布双层次级声源并适当增大轴向层间距，能够以相对较少的次级声源实现对高阶模式声波的控制。

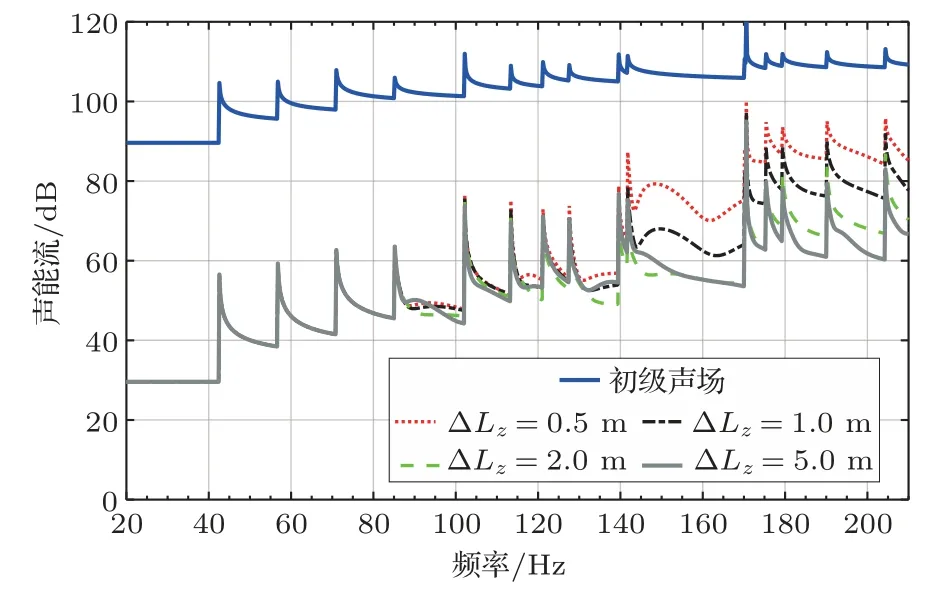
图7 壁面分布双层次级声源的不同轴向间距对高阶模式声波的控制效果Fig.7 The control performances achieved by different axial spacings of the boundary-located double-layer secondary sources

本节的仿真实验模拟了理论模型中所述几种典型的壁面分布次级声源的控制性能。仿真结果显示，壁面分布次级声源控制高阶模式声波的工作频率范围明显受限于次级声源的空间分布。其中，仅沿x方向分布的次级声源，其工作频率上限不超过(0,2)模式声波的截止频率；仅沿y方向分布的次级声源，其工作频率不超过(2,0)模式声波的截止频率；同时沿x和y方向分布的次级声源的工作频率上限则可以提高至(2,2)模式声波的截止频率。根据理论模型推理可得，这是因为次级声源沿x和y方向的空间分布对高阶模式声波的贡献只能控制mx和my相关的高阶模式，且由于对于矩形管道在x和y方向只有两面墙，使得在x和y方向最多控制两个不同的高阶模式。此时，在更高频率段次级声源对高阶模式的控制性能主要取决于其轴向分布范围。当次级声源在管道轴向上范围较大时，能显著提高对高阶模式声波的控制效果。

在理论模型中通过将次级声源的分布离散化，根据采样定律也能得到次级声源在各方向上的数量和间距对控制效果的影响。壁面分布次级声源在管道周向上的数目及间距需要满足采样定律，但更多的次级声源会导致过采样，对提升控制效果没有帮助。在管道轴向上，尽管壁面分布次级声源在轴向间距过大时可能造成控制性能下降，但由于增大了轴向分布范围因此整体上依然能提高控制性能。

3 结论

针对管道有源噪声控制中的壁面分布次级声源空间分布优化设计问题，本文提出了壁面分布次级声源独立控制高阶模式声波的理论模型，显式推导了次级声源的空间分布对于控制高阶模式声波的贡献，分别指出次级声源在管道周向和轴向空间分布的优化准则；然后通过将次级声源空间分布离散化介绍了点声源控制策略，并根据采样定律分析了次级声源的数目和间距对于控制效果的影响。通过对比多种次级声源空间分布以及对应的控制性能，其结果表明为了优化壁面分布次级声源的空间分布，需要在管道周向所有壁面布放足够数量的次级声源以满足采样定律，同时在轴向上增大间距来获得较大的分布范围。