基于三维数字图像相关法应力测量技术

袁 媛 孙增玉 王 杏 高 越 刘 柯

(北京航天计量测试技术研究所，北京 100076)

1 引 言

在航空航天飞行器研制领域，通过风洞模型试验研究飞行器性能，降低飞行器研制风险和成本。在雷诺数模拟能力相同的情况下，相比于常规风洞，低温风洞显著降低了风洞尺寸及对洞体结构的强度要求，风洞造价也随之降低，所需动压、驱动功率、峰值功率和总能消耗降低。由于低温风洞运行环境复杂性，相关实验研究仍处于探索阶段，风洞天平是测量风洞中气流作用在模型上的气动力和力矩的测量设备，可以实现气动力和力矩沿三个坐标系分解并精确测量。但风洞天平的测量精度受低温风洞内运行温度及运行环境的影响较大，诸如低温下传感器材料的特性变化、低温下应变片零点及工作灵敏度的温度补偿难以得到有效控制等。因此急需针对超低温高速风洞的特殊试验环境，研究飞行器应力的高精度测量技术，以非接触测量的方式解决超低温风洞下模型状态测量，为飞行器试验提供必要检测手段[1,2]。

与二维数字图像相关不同，三维数字图像相关法可以实现被测模型的全场高效三维形貌和变形测量，且不需要二维数字图像相关法中对于测量相机的光轴与被测模型表面相垂直和被测模型主要为面内形变等条件约束，其主要优点有非接触高效光学精密测量、大量程动态实时测量、高精度多参数同步测量，整个测量光路简单且适合于特殊运行环境下的应力测量。本文直接利用被测物体表面人工形成的随机散斑图案在变形前后参考和目标图像子区的灰度变化来获取模型表面的三维位移场和应变场，进而获得模型在低温环境下的应力场。

2 三维数字图像相关方法

三维数字图像相关法是采用两台高速摄像机同步采集被测模型表面图像，结合双目立体视觉进行变形测量的一种光学非接触高精度测量方法[3,4]。其基本思想是通过拍摄和处理被测模型图像子区变形前后二维图像获得被测模型表面的三维位移和应变分布。三维数字图像相关法通过匹配被测模型变形前后两幅散斑图像中的不同图像子区来计算三维位移场，通过数值微分计算获得应变场[5～7]。

2.1 双目视觉成像模型及相机内外参数标定

双目视觉技术的主要原理是基于视差来实现，利用两个空间位置姿态关系已知的相机在不同方位下同时采集被测特征的图像，通过图像处理及同名点匹配等技术获取被测特征对应的同名像点对，利用相机成像模型建立成像光线方程，构建光线三角交会约束，组建双目视觉测量数学模型，解算被测特征空间三维坐标[8]。双目立体视觉测量原理示意图如图1所示。

图1 双目立体视觉测量原理示意图Fig.1 Schematic diagram of binocular stereo vision measurement principle

(1)

式中：R——o-xyz坐标系与or-xryrzr坐标系间的旋转矩阵；T——两坐标系间的平移矩阵。

空间三维坐标可以表示为

(2)

已知焦距fl、fr和空间点在左右相机中的图像坐标及旋转矩阵R和平移矩阵T，可解算空间任一点的坐标。

双目相机内外参数标定是基于三维数字图像相关法解算应变的前提，标定结果的好坏影响到最终的测量结果。相机标定就是为了正确建立空间中某点和它在图像平面上对应像点之间的关系。相机标定包括两部分，分别为内参数和外参数标定，内参数即相机和镜头的畸变相关参数，主要有主点位置、焦距、等效像素、畸变因子等；外参数即两相机坐标系间的空间转换关系，包括位置关系和角度关系。根据透视投影关系有

s=A[RT]

(3)

式中：s——任意的非零尺度因子；——图像平面上的二维点坐标的齐次坐标；A——相机内部参数矩阵；——平面模板上的三维点坐标的齐次坐标。

(4)

假设有n幅标定图像，每一幅标定图像上有m个特征点，则建立非线性优化模型为

(5)

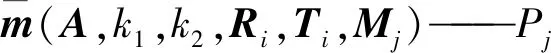
将每幅图解得的A,Ri,Ti及每点对应的图像和世界坐标点对，畸变参数k1,k2的初值为0，通过非线性优化得到全局最优解。

2.2 立体匹配

如图2所示，左图为物体变形前散斑图像，右图为物体变形后的散斑图像，在左图中选取以某待求点P(x0,y0)为中心的像素尺寸为(2M+1)×(2M+1)的矩形参考图像子区，在变形后图像中选取若干个相同大小的样本子区进行逐一比对匹配，按标准化协方差互相关系数的计算结果，以寻找与协方差相关系数绝对值为最大时对应的目标图像子区点P′(x′0,y′0)，确定x和y方向的位移分量。在利用数字图像进行实际计算时，以虚拟网格的形式对测量图像进行划分，求得每个虚拟网格节点的位移来获取全场三维应变场。

图2 物体变形前后参考图像子区和目标图像子区Fig.2 Reference image sub-region and target image sub-region before and after object deformation

变形前后图像子区之间的协方差相关系数C为

(6)

一般来说，与参考图像子区相比，目标图像子区的中心位置和形状都会发生改变。在采用一阶函数的情况下，参考图像子区中的某一点Q(x,y)与目标图像子区中对应点Q′(x′,y′)之间存在一定的函数关系，即形函数为

(7)

式中：Δx和Δy——点(x,y)到P(x0,y0)的距离；u和v——参考子区中心在x、y方向上的位移；ux,uy和vx,vy——图像子区的位移梯度。

由公式(7)求出变形后图像搜索区域中所有目标子区中心点在x、y方向上的位移和位移梯度的值，就可以得到模型表面的三维位移量和变形值。由于高速相机采集得到的测量图像灰度信息是离散的，因此在目标子区搜索时位移只能以整像素为单位来进行，然而物体真实的位移值或变形值并不一定是像素的整数倍，采用亚像素搜索算法，通过对相关系数矩阵做曲面拟合运算，由拟合曲面的极值点解算得到亚像素级别的位移量，提高被测模型三维位移和变形的测量精度。

3 应力测量系统设计

采用双目立体视觉和数字图像相关技术可实现低温环境下被测试件应力参数的现场测量，测量装置由两台高速相机、散斑喷涂装置、被测试件、图像处理计算机及测量软件组成。其中，两台高速相机型号为V1612，最高帧频可达16000帧/s，分辨率为1280×800，像元尺寸为28μm，均可满足测量图片的高速高分辨采集的要求，其应力测量示意图如图3所示。

图3 应力测量示意图Fig.3 Schematic diagram of stress measurement

测量时，先对双目测量系统进行标定，确定相机内参数和两台相机坐标系间的空间转换关系(相机外参数)，构建全局坐标系，求解被测模型坐标系与全局坐标系的空间关系。根据测量需要，可在风洞的观察窗处架设一套双目视觉系统。测量过程中，基于电路输出TTL信号给两相机的外触发接口，同步触发装置同时触发两台高速摄像机。在被测模型上喷涂散斑图案，利用两台高速数字相机同时采集变形前后的散斑图像。被测试件在风洞内环境和温度变化过程中，被测系统以16kHz的采样频率对试件的空间姿态进行实时测量，两个高速相机同步采集测量图像，传输到数据处理系统进行分析和解算，通过立体匹配精确获得左右相机对应子区中心点的精确匹配，结合双目立体视觉测量模型解算各点在全局坐标系下的空间三维坐标。

在高马赫数风洞试验条件下，不可避免会产生抖动现象，对视觉系统的姿态测量精度会产生影响。在风洞试验程中被测模型发生的运动实际上是一个抖动和姿态变换的复合运动，本文采用运动分离的方法，通过监视被测模型固定架自身的抖动，把该抖动量从飞行器实际运动中消除，获得被测模型的运动参数。针对风洞试验的具体环境，在风洞侧壁安装固定参考点，通过固定点反推相机的抖动量和飞行器的抖动量，将抖动量从复合运动中减掉，即可获得被测模型真实的姿态变化。

在变形前，可选取左相机测量图像中要计算的对应图像子区，通过立体匹配可得到右相机对应的图像子区，基于视觉原理可得到该子区中心点在T0时刻的空间三维坐标(x0,y0,z0)；变形后，基于图像数字相关法分别找到左、右相机对应的目标子区，得到T1时刻变形后的子区中心点的空间三维坐标(x1,y1,z1)；变形前后图像子区中心点的三维坐标的差，即为所求的三维位移，平滑后通过差分计算求得相应的应变场。在应力参数测量中，风洞条件下应力不能直接测量得到，但由力引起的应变可获取得到应力量。

4 三维数字图像相关法算法

立体匹配是双目视觉中的难点，主要涉及两种匹配：第一种是左相机测量图像集的相关匹配，与二维数字图像相关法中的相关匹配原理相同；第二种是左右相机测量图像集之间的相关匹配，两相机的测量图像存在视差。整个方案的立体匹配算法流程图如下图4所示。

图4 立体匹配算法流程图Fig.4 Stereo matching algorithm flowchart

首先，对左、右相机进行内外参数标定，读取左右相机图像，以左相机第一幅测量图像作为左相机测量图像系列匹配的参考图像，也作为右相机测量图像集的参考图像，实现左相机图像间的匹配、及左右相机对应图像间的匹配。以计算点为中心，截取一定大小的参考图像子区和目标图像进行Shift初值估计，迭代收敛计算。若满足迭代收敛条件，则利用形函数计算得到该计算点的上、下、左、右四个点的初值估计点，计算所有网格点，通过三维重建得第k幅图像计算点的三维坐标值。

5 试验与分析

试验装置由薄壁圆形平板试件、两台高速相机、同步触发装置、高低温试验箱和图像处理计算机组成。其中，试件材料为5A06铝合金，其弹性模量为70GPa，试件直径为160mm，厚度为2mm。将试件放置于高低温实验箱内，在试件表面喷涂散斑，架设双相机同步采集测量图像，通过立体匹配算法进行图像子区的相关匹配，获得不同温度条件下试件上多点的三维坐标值，并解算得到试件在-30℃时多点的应变值，被测试件在常温下和-30℃下的点的三维坐标值数据、被测试件在温度下降到-30℃时多点应变值数据见表1所示。由变形前后试件表面的三维坐标值通过后续解算可得到试件表面的应变场。图5(a)为在常温下，试件表面11个点的三维坐标值解算图，当温度下降为-30摄氏度时，通过立体匹配算法对测量图像进行多点的相关匹配，计算得到试件表面多点的三维坐标值解算图，如图5(b)所示。

图5 常温下和-30℃下试件表面多点的三维坐标值Fig.5 Coordinate values of multiple points on the surface of the specimen at room temperature and-30℃

由试验可得，基于三维数字图像相关算法实现了左相机测量图像集的相关匹配，及左右相机测量图像集之间的相关匹配，完成了被测试件表面点的立体匹配及应力测量。

6 结束语

本文探讨了基于高速三维图像数字相关法的模型应力测量方法，结合立体匹配算法可获得变形前后物体上计算点的三维坐标值，可得模拟表面的应力场分布，为解决低温风洞下模型状态测量问题提供一种可行的测量方法。

表1 常温下和-30℃下被测试件多点的坐标值及多点应力值Tab.1 Solutioncoordinatevalueofthespecimenatroomtemperatureand-30℃andstrainvaluesofmultiplepoints常温下x(mm)y(mm)z(mm)-30℃x(mm)y(mm)z(mm)应变值应力值(GPa)点132.23536.9840.119点132.29536.8430.0560.075%0.0525点235.4835.2670.096点235.5225.1580.0130.106%0.0742点336.944-31.8920.009点336.979-31.978-0.0810.195%0.1365点4-0.00265.7700.114点40.06365.6310.0710.092%0.0644点50.58923.8220.232点50.65023.7040.1840.153%0.1071点62.142-15.6330.163点62.189-15.7240.1340.144%0.1008点7-3.384-55.0060.003点7-3.344-55.089-0.0290.207%0.1449点8-42.55957.344-0.052点8-42.47357.226-0.1330.111%0.0777点9-44.65016.3660.158点9-44.56116.2420.0850.092%0.0644点10-35.365-22.6020.064点10-35.297-22.6980.0290.114%0.0798点11-75.895-9.206-0.093点11-75.825-9.299-0.1110.130%0.0910