CTRM加固震损短肢剪力墙连梁抗弯性能研究

蒋隆敏，刘 奥，竹永恒，龚 鑫

（湖南工业大学 土木工程学院，湖南 株洲 412007）

0 引言

碳纤维具优异的抗拉性能，可被用于建筑材料加固中，较多科研工作者对此进行了研究[1-8]。碳纤维板材、布材、筋材用于结构加固的技术现已比较成熟，工程上也得到了广泛运用，但存在一定的局限性。使用碳纤维网增强的高性能复合砂浆（CTRM）加固建筑结构有较多优势，也是当前的热门研究领域之一，但是将其用于连梁加固的研究现还处于空白。

实际工程应用中，有些建筑结构因使用年限增长及地震作用等影响，造成连梁损坏，梁根部产生较大弯矩，导致混凝土开裂，最终导致整个构件被损坏。当发生地震时，构件的连梁根部会形成塑性铰，通过它的转动消耗能量，而且墙体前产生的弯曲破坏为第一道抗震防线，因此，有必要对发生震损后的短肢剪力墙连梁进行修复加固处理，并对加固后的连梁抗弯性能进行研究。

本文拟对CTRM 加固震损短肢剪力墙连梁模型进行试验研究，然后在此基础上对其进行有限元分析，得出加固研究结论，以期为CTRM 的工程运用提供一定的理论参考。

1 试验设计

1.1 模型设计、制作和预损

本研究中短肢剪力墙试验模型，取自结构中间层边节点的上下反弯点处，连梁取自中间层反弯点处，地震作用下的试验模型和具体受力情况见图1。

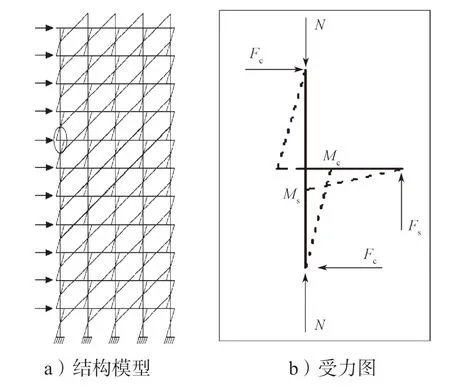
图1 地震作用下的弯矩图和试验模型的选取Fig.1 Selection of bending moment diagram and test model under earthquake action

此次试验制作了2 个缩尺比例为1∶3 的“T”型带连梁短肢剪力墙试验模型，其具体尺寸和配筋详见图2 和3。

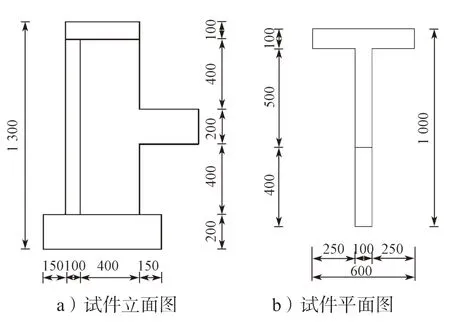
图2 模型尺寸图Fig.2 Test model size

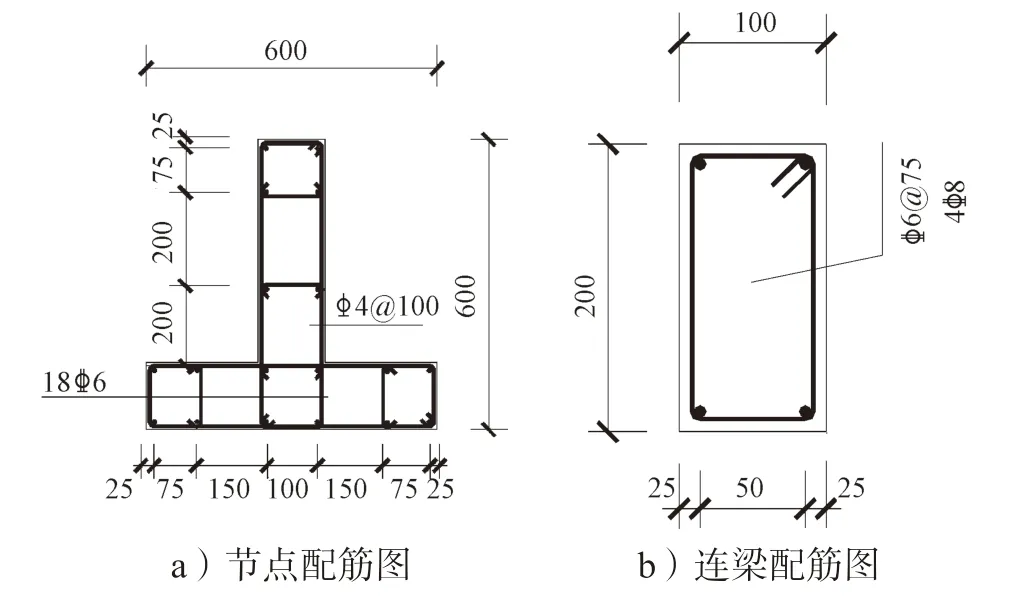
图3 模型配筋图Fig.3 Model reinforcement drawing

本研究中，命名两个初始试验模型为S1和S2，遭震损破坏并被修复加固后的试验模型为R1和R2。分别对初始模型S1和S2的连梁端部施加不同荷载，使两个模型产生不同程度的震损[9]。

试验中测得初始试件S1和S2的混凝土抗压强度均值分别为28.22 MPa 和29.22 MPa。震损加固后试件R1和R2的高性能复合砂浆抗压强度均值分别为35.7 MPa 和34.8 MPa。

本试验中，S1模型为严重受损试件，其轴压比为0.3，预损后梁根部出现大量裂缝，混凝土被压碎，梁内纵向钢筋屈服并发生滑移现象；S2模型为轻微受损试件，其轴压比为0.3，预损后梁根部出现了裂缝，混凝土因挤压而出现轻微开裂现象，梁内钢筋没有屈服。试件预损后，采用碳纤维网增强的高性能复合砂浆对两个试验模型进行修复加固处理，两者的加固方式相同。

1.2 试件加固方案

首先，在连梁根部和腹板与连梁交接处铺设两层200 mm×100 mm 的L 形碳纤维网格，将其布置在梁的上下两侧。为了防止梁根处的碳纤维网脱落，在梁根处环形缠绕两层宽度为100 mm 的碳纤维网；为了防止腹板网格脱落，取2 层400 mm×100 mm 网格，紧贴在墙腹板处至腹板处的内侧网格上，然后用预设钢板和螺钉锚固。具体试验模型设计的加固方式如图4 所示。

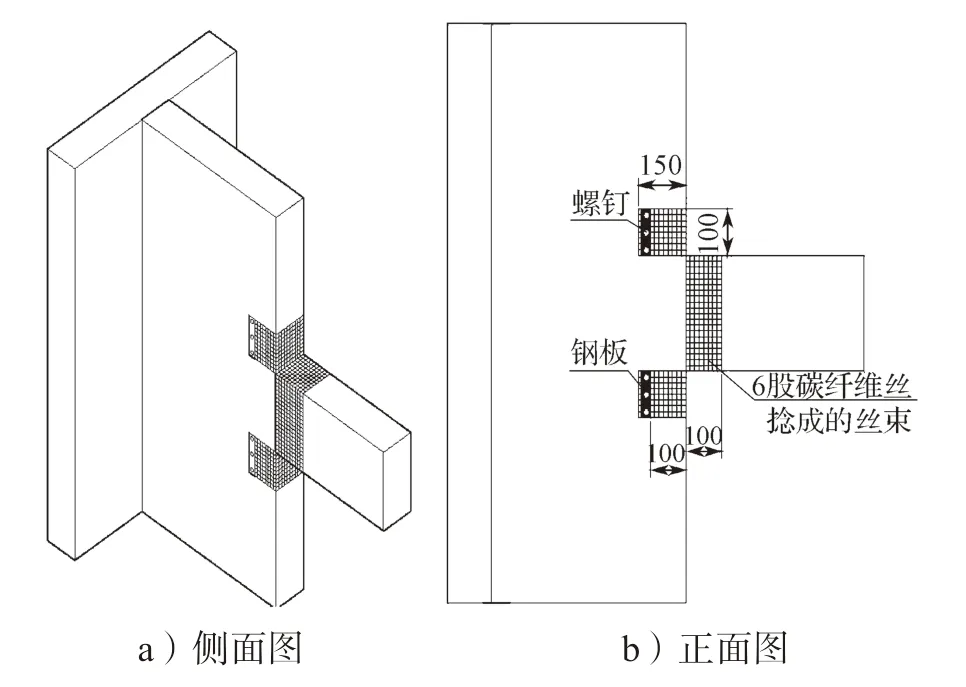
图4 试件加固方案Fig.4 Reinforcement scheme of specimen

1.3 试件加固施工工艺及要点

实际结构工程应用中，当需要对构件进行加固时，恒载和活荷载并不能够被完全消除，故模拟试验模型的墙体所承受的轴压荷载不变情况下进行加固，即进行二次受力加固。根据已有的构件加固规程及相关文献[10-12]，本研究使用CTRM 对震损短肢剪力墙连梁进行修复加固，施工工艺及加固步骤如下。

1）凿毛及钻孔。首先，对标记的区域进行凿毛处理，凿至其表面漏出粗骨料。同时，在槽内对钢板孔距相应的部位钻孔，并清除混凝土外部的抹灰和松动的细小石子。

2）凿毛面清洗。先用钢刷对混凝土外部松动的石粒进行清除，再用压力水枪对待加固区域进行反复地冲洗、冲刷，直至无杂质浮尘和松动的细小石块。

3）布置碳纤维网。将裁剪好的碳纤维加强塑料（carbonfiber-reinforced plastics，CFRP）网格布置在加固区域，用加工好的钢板将网端部压紧，网格搭接区域用钢丝绑扎，并用螺丝锚固。

4）涂抹界面剂。先洒水湿润混凝土表面，然后用毛刷在构件加固区的表面涂抹界面剂，涂抹界面剂时需要使用毛刷对CFRP 网进行反复地挤压摁实，以防止漏涂，且应在保证没有漏涂的前提下，尽量使界面剂涂刷均匀。

5）涂抹高性能复合砂浆。砂浆涂抹通常分3 次进行，且第一次尤为重要。第一次涂抹即在CFRP 网格及加固区域混凝土表面孔洞用砂浆填实；第二次用高性能复合砂浆覆盖所有的CFRP 网，让砂浆和CFRP 网形成良好的有机整体，共同受力；第三次涂抹是为了使加固层厚度达预设要求。涂抹完成后还需对加固层表面进行平整。

6）浇水养护。先将试件刷白以便于后续观察裂缝的生成情况，然后在自然环境下养护28 d，定期洒水保持试件表面湿润。

1.4 试验加载装置

试验加载装置如图5 所示。

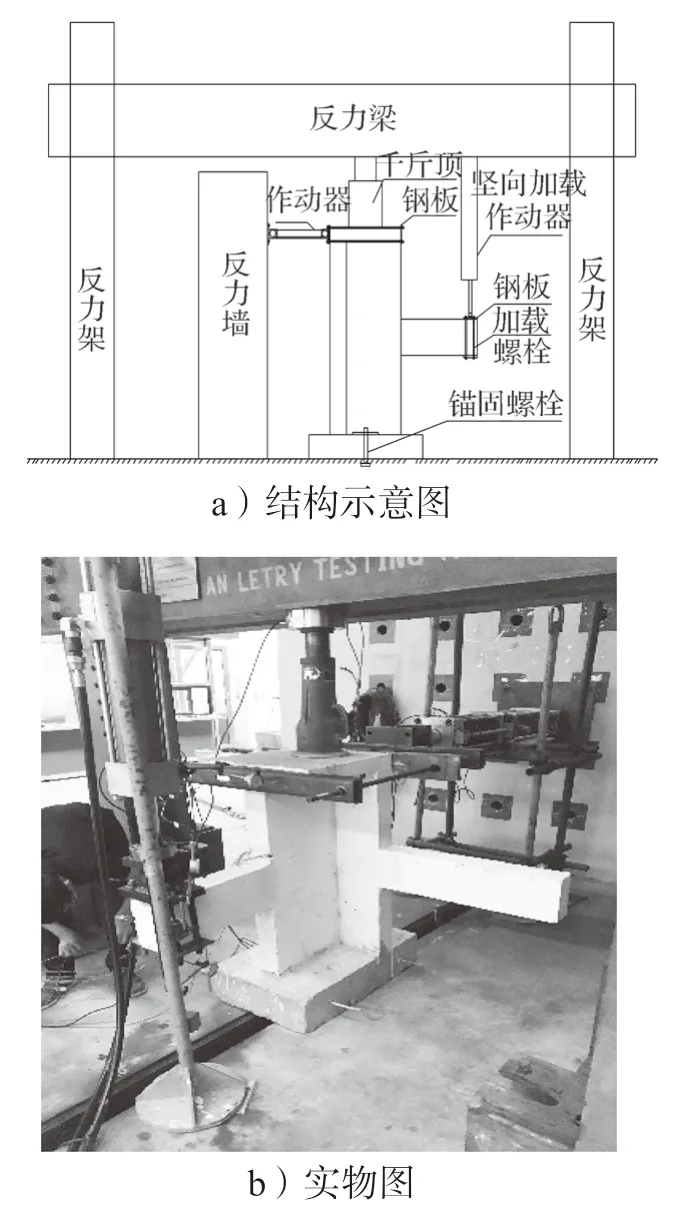
图5 试验加载装置图Fig.5 Test loading device diagram

1.5 试验加载制度

本研究中采用荷载-位移的混合加载制度。在构件梁端施加竖向的周期荷载，且每级循环一次[13]。当剪力墙连梁出现明显裂缝时停止加载，此时的荷载定义为开裂荷载[14]。当进行位移控制阶段时，以梁端竖向位移Δ 作为位移加载阶段的加载基数，按其倍数逐级循环进行，并且每一级循环两次[13]。当模型的最大承载力降低至极限荷载的85%时，停止加载，定义此时的荷载为破坏荷载，并定义破坏荷载对应的位移为极限位移，结束试验[15]。具体的加载制度如图6 所示。

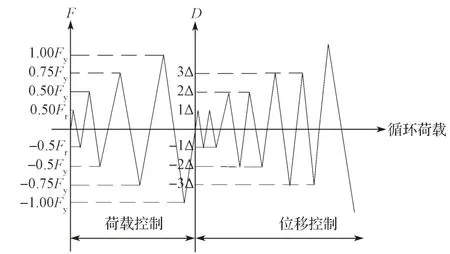
图6 试验加载制度示意图Fig.6 Test loading system

2 试验结果与分析

2.1 模型破坏形式分析

1）试验模型S1。当力加载到14 kN 时，连梁根部出现了一条竖向裂缝，即为开裂荷载。在位移控制阶段，当其级数达6Δ 时，混凝土被压碎，脱落，梁根部裂缝宽度扩大，但是连梁侧面没有斜裂缝产生，试验模型呈现弯曲破坏。

2）试验模型S2。当力加载到13 kN 时，连梁根部右侧面出现竖向裂缝，左侧面出现人字形裂缝，此时梁端竖向位移为9 mm，因对S2所需预损程度较轻，故停止加载。

3）加固试验模型R1。当力加载到16 kN 时，在连梁根部加固层中出现一条裂缝，即为开裂荷载。在位移控制阶段，当位移增加至5Δ 时，连梁根部上下方竖向裂缝连通，混凝土有脱落迹象，且混凝土被压碎，当位移增加至6Δ 时，梁根部和腹板加固层裂缝宽度明显增大，此时承载力降到极限承载力的85%，加固试验模型S1仍表现为弯曲破坏。

4）加固试验模型R2。当力加载到21 kN 时，连梁根部加固层区域出现一条裂缝，即为开裂荷载。在位移控制阶段，当位移增加至6Δ 时，连梁根部上下方竖向裂缝相连。当位移加载至8Δ 时，承载力降到极限承载力的85%，连梁根部裂缝较多，但连梁侧面未产生斜裂缝，至试验结束，加固层未出现剥离，试验模型R2仍表现为弯曲破坏。

各试件的最终破坏形式如图7 所示。

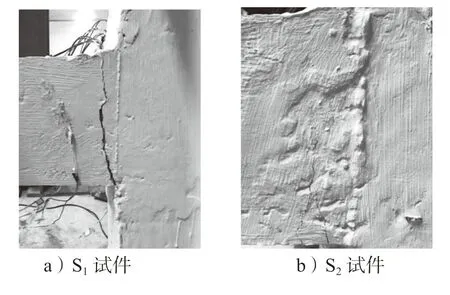
图7 试件破坏形式Fig.7 Failure mode of specimen

由图7 可知：R1和R2的连梁根部混凝土有脱落迹象，但未发生加固层剥离，CFRP 网格仍保持良好，未被拉断。

2.2 模型滞回曲线及耗能分析

对结构的抗震性能进行研究时，常采用绘制其滞回曲线的方法。本研究所得各实验模型的滞回曲线详情如图8 所示。

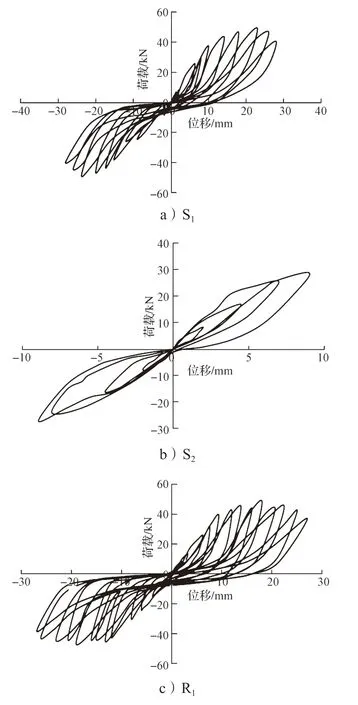
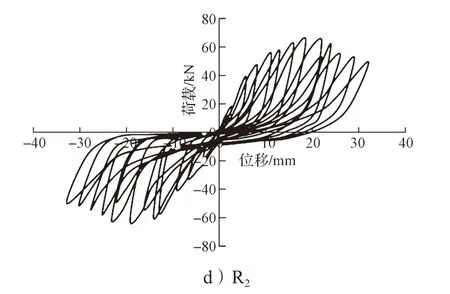
图8 各试验模型的滞回曲线Fig.8 Hysteresis curves of each test model

1）对比试验模型R1与S1的滞回曲线，发现都有“捏缩”现象，且两者的变化趋势基本上是一致的，但是相较而言，模型R1的曲线更加饱满，这说明加固后其延性和耗能要更好。

2）加载初期，各试验模型都为弹性阶段，加固层未发挥作用，残余形变和刚度退化不明显。加载至弹塑性阶段时，滞回环的面积越来越大，表明连梁的钢筋黏结滑移越来越严重，连梁端部的荷载没法得到有效传递，导致曲线发展呈现出“S”型。

3）从抗弯承载力方面对试验模型进行分析，可知预损程度较重的R1试件的极限荷载能基本恢复到原来的试验模型水平，而预损较小的R2试件的极限荷载提升幅度较显著，说明采用CTRM 对震损短肢剪力墙连梁进行修复加固，能有效提升其抗弯承载力，且震损越轻，改善效果越明显。

2.3 骨架曲线分析

骨架曲线是研究构件抗震性能的一项重要指标，本实验测得各试验模型的骨架曲线详见图9。分析图9 可以得知，各试验模型的骨架曲线变化趋势在加载初期较为接近，说明均处于弹性状态。R1由于震损严重，其延性与S1比较而言改善不明显。而R2相对于R1，其抗弯承载力和极限位移均有较为明显的提升，这一结果说明，随着震损程度的加重，加固后试件的承载力和延性改善幅度减小。

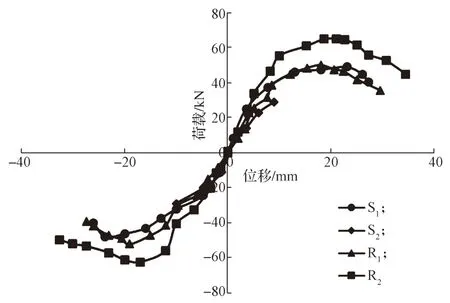
图9 各试验模型的骨架曲线Fig.9 Skeleton curves of each test model

2.4 抗弯承载力及延性分析

对所得试验模型的性能指标数据进行归纳总结，整理于表1 中。

表1 各试验模型的性能指标Table 1 Performance index of test model

分析表1 中的数据，可知试件S1和试件R1相比，其抗弯极限荷载基本一致；而试件R1与试件R2相比，试件R2的屈服荷载提高了43.4%，延性提高了9.3%，抗弯极限荷载提高了31.0%，极限位移提高了20.4%。

3 模拟分析结果与试验结果对比

3.1 单元选取及材料本构模型

本研究中高性能复合砂浆和混凝土构件均采用SOLID65，钢筋取Link8 单元，加固层材料CFRP 网表现为抗拉，故选Link10，刚性垫块选SOLID65 单元。碳纤维网的屈服强度为5.3×103MPa，弹性模量为2.1×105MPa，钢筋屈服强度为290 MPa，弹性模量为2.1×105MPa；混凝土弹性模量为2.55×104MPa，高性能复合砂浆的弹性模量为3.2×104MPa，材料的泊松比均为0.3。

3.1.1 复合砂浆与混凝土本构关系

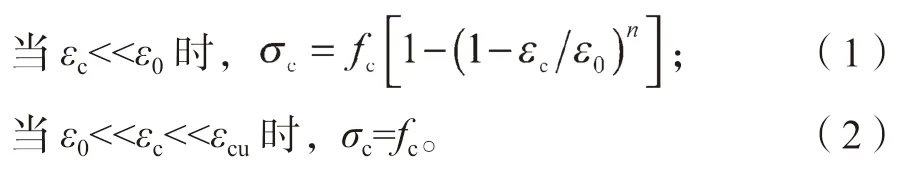
式（1）（2）中：εcu为混凝土极限压应变，取0.003 3；ε0为当混凝土压应力达到fc时的应变，取0.002；n为系数，该系数最大取值为2；fc为混凝土抗压强度设计值；σc为当混凝土压应变为ε0的压应力。

3.1.2 钢筋本构关系

数值分析中选用双线性等向强化模型BISO 为试验模型钢筋，其应力-应变关系如图10 所示，应力-应变计算公式如下：

式中：σs为钢筋拉应力；εy为钢筋屈服应变；Es为钢筋线弹性模量；fy为钢筋屈服应力。

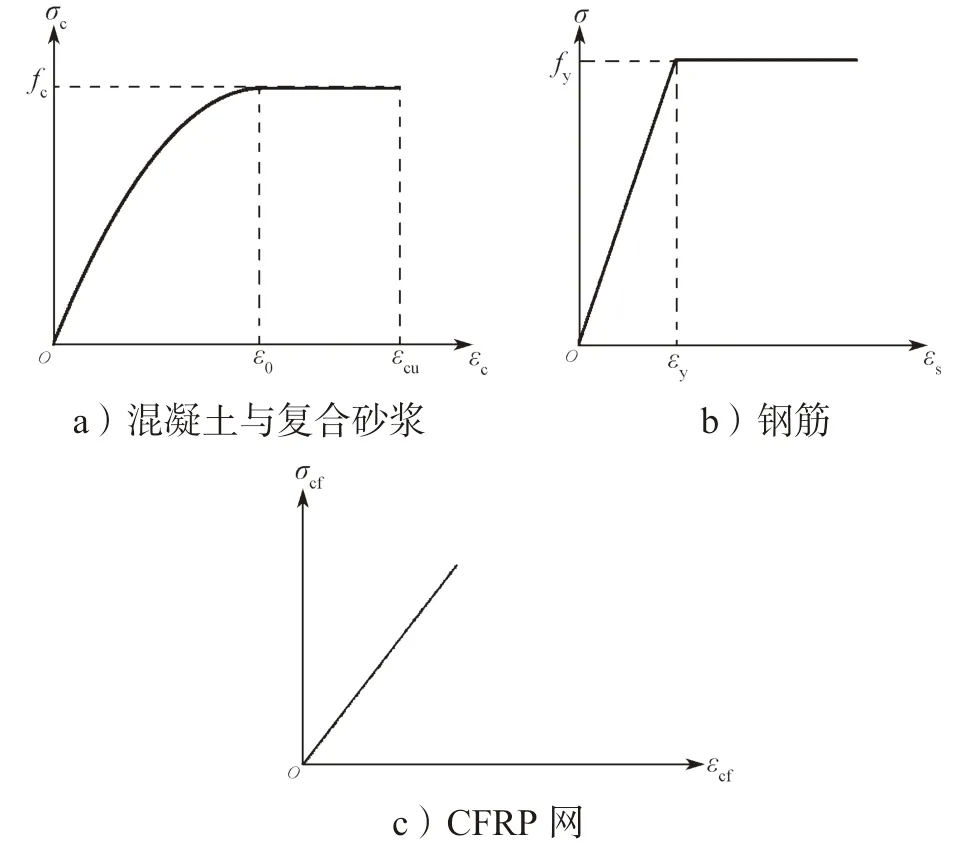
图10 材料应力-应变曲线Fig.10 Material stress-strain curve

3.2 有限元模型建立

采用分离式建立有限元模型，忽略钢筋与混凝土间的黏结滑移，共建立如图11 所示原试验模型与加固层模型两种有限元模型。

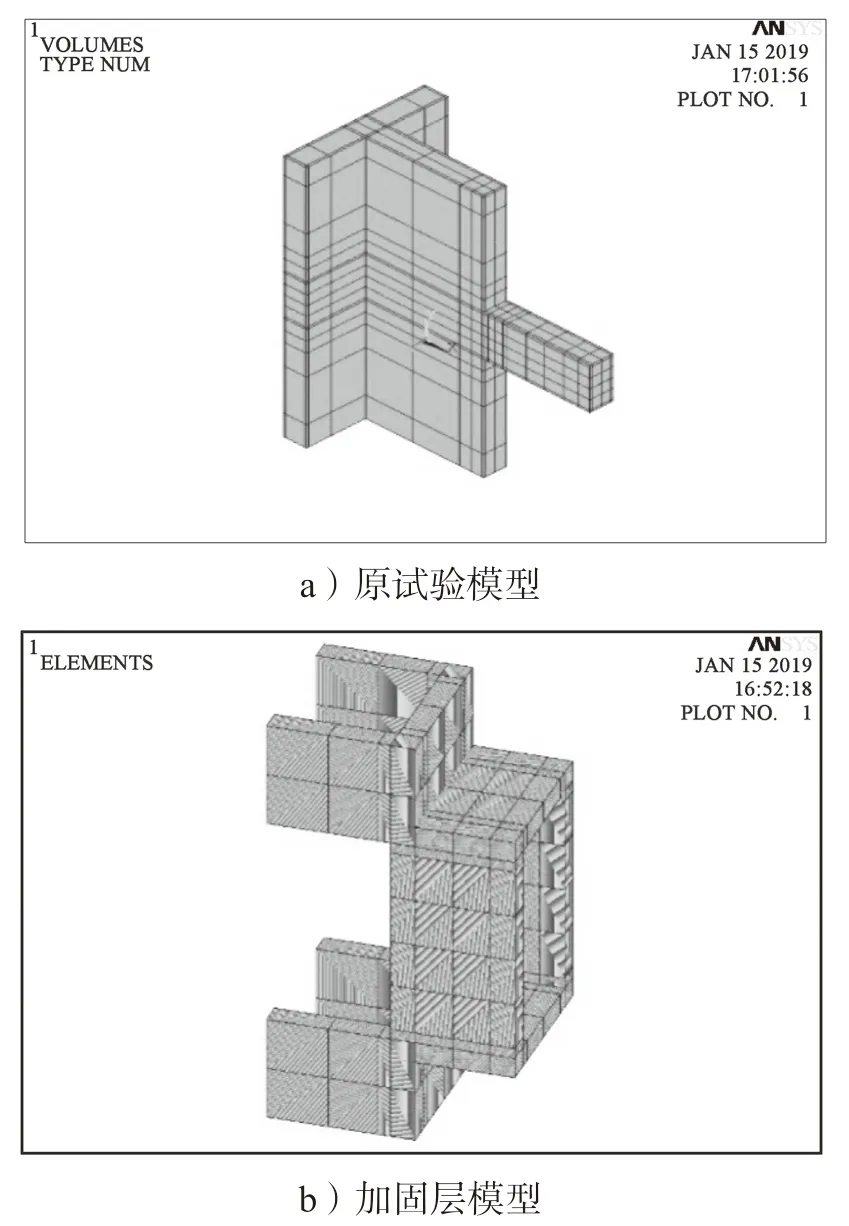
图11 试件的有限元模型Fig.11 Finite element model of test specimen

3.3 有限元模型加载与求解

为模拟短肢剪力墙连梁上下层反弯点间的约束状况，对模型底部x、y、z 方向均加以约束，对其顶部给予y 和z 方向上的约束，在模型顶面施加轴压力，并且维持轴力不变，试验模型连梁端部竖向低周往复加载方法通过荷载步文件加载。针对试验中震损加固模型的模拟，即在建模时已将加固层建好，在试验模型震损及卸载阶段，通过“杀死”加固层，以模拟对其震损加载过程；在对震损试验模型加固后的二次加载阶段再“激活”加固层单元，以模拟震损加固试验模型的加载过程。图12 所示为施加边界约束的试验模型。

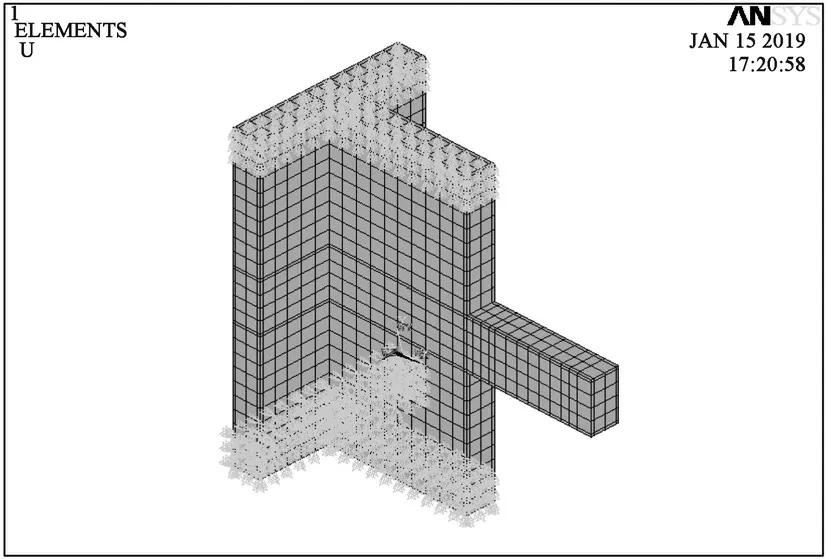
图12 边界约束与加载条件Fig.12 Boundary constraints and loading conditions

3.4 数值模拟和试验数据的滞回曲线对比分析

各试验模型的数值模拟和试验数据的滞回曲线详见图13。

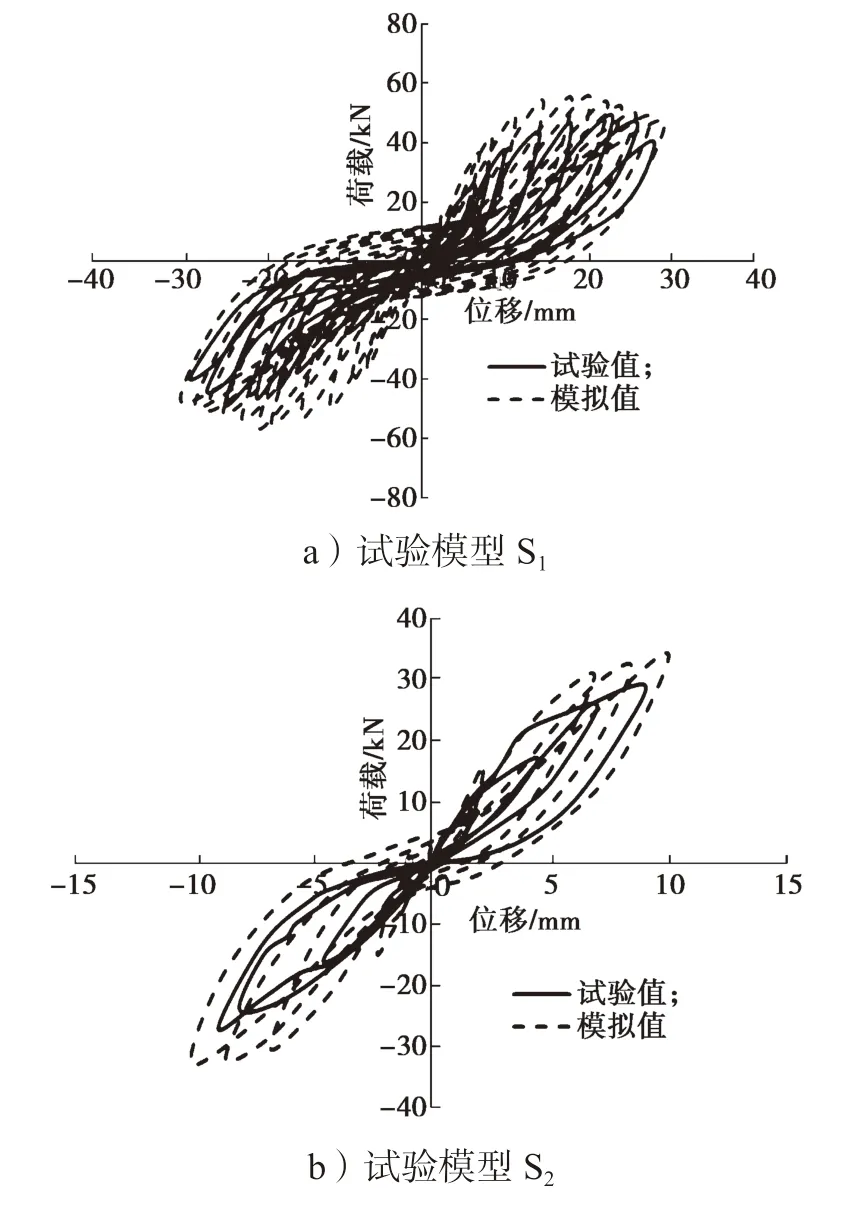
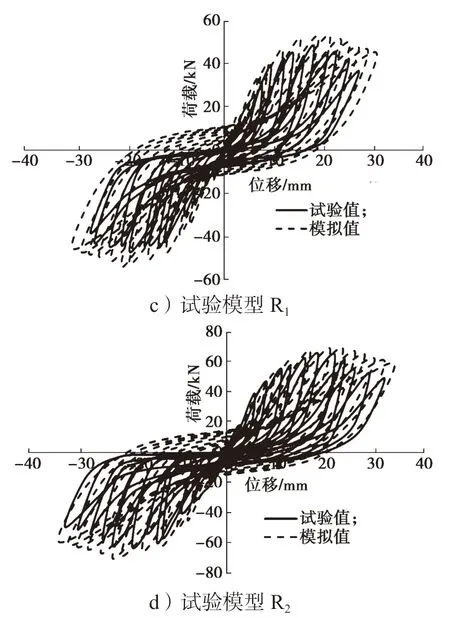
图13 数值模拟和试验数据滞回曲线对比图Fig.13 Hysteretic curve comparison chart

通过对比图13 中各滞回曲线可知：各模型试验值和模拟值的滞回曲线差异不大，较为吻合。从各滞回曲线中可以看出，数值模拟所得试验模型的极限荷载比试验所得荷载要大，这可能是因数值模拟中各材料较试验所用材料更均匀，且未考虑钢筋、混凝土间的黏结滑移。

3.5 数值模拟和试验数据的骨架曲线对比分析

将用ANSYS 模拟所得试验模型滞回曲线的各循环最大荷载点依序连成一条曲线，拟定为试验模型骨架曲线，详情见图14。

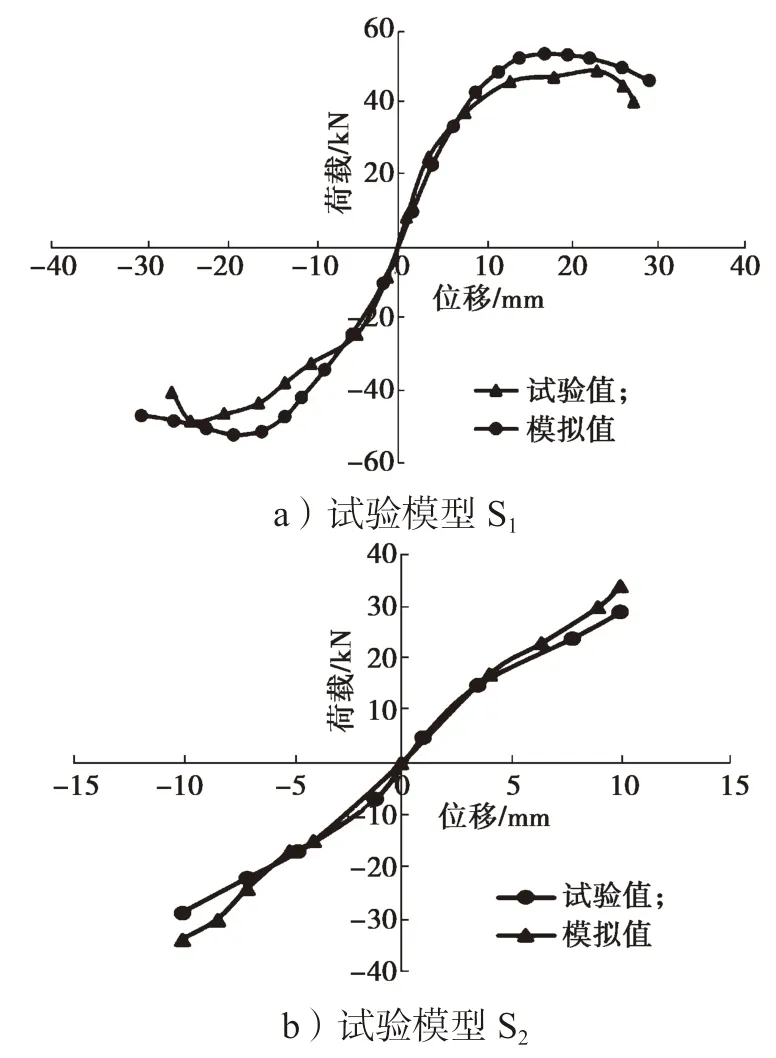
图14 数值模拟和试验数据骨架曲线对比图Fig.14 Skeleton curve comparison chart

通过对比图14 中各试验模型骨架曲线：发现在加载初期，试验值和模拟值都呈线性变化，但后期出现不大的差别，其模拟承载力数据比试验数据大，这可能是因数值模拟采用的混凝土材料较均匀，且不考虑混凝土、钢筋间的黏结滑移。试验和模拟的骨架曲线，均体现出如下规律：即相较于原试验模型，震损后加固的试验模型的抗弯承载力、延性、耗能等性能都有不同程度的改善。

3.6 连梁抗弯承载力试验值与模拟值比较

表2 给出了各试验模型的最大抗弯承载力试验值和模拟值。但由于S2的震损相对较轻，其连梁抗弯承载力没有达到极限值，所以没将其列入表2 中。分析表2 中的数据可知，最大抗弯承载力的试验数值比模拟获取的数值要略小，这可能是因为对模型进行了简化造成的，但是数据间相差都不大，这表明所提对遭受荷载损伤的短肢剪力墙连梁抗弯加固设计及计算可以起到一定的参考作用。

表2 最大抗弯承载力试验值和模拟值Table 2 Test and simulation values of maximum flexural capacity kN

4 结论

本文基于两个缩尺比例为1∶3 的“T”型带连梁短肢剪力墙试验模型，在不卸轴力下用CTRM 对两个试验模型进行二次受力加固，结论如下：1）采用CTRM 加固带连梁的短肢剪力墙是一种有效加固方案，加固后连梁的承载力、延性、耗能性能都明显提高，说明加固处理能提高连梁抗震性能。2）整个试验过程中，试件未出现加固层剥离现象，表明本试验所采用的加固方案及锚固方法是行之有效的。3）模拟结果和试验结果中，所得滞回曲线和骨架曲线总体相差不大，体现了建模的可靠性。

本文总结出的一套使用CTRM 加固震损短肢剪力墙连梁的施工工艺流程，对于实际工程结构加固有一定的参考价值。