仿蚱蜢跳跃机器人腿部结构设计与性能分析
熊勇刚,成 威,龚 琦,田万鹏
(湖南工业大学 机械工程学院,湖南 株洲 412007)
1 研究背景
相比于轮式、步行和履带式等移动模式,跳跃运动具有更好地适应非结构化地形、更加快速地越障和避让危险的优势。因此,在察探地形、探寻矿石和侦探敌情等领域之中,跳跃机器人拥有广阔的应用前景[1]。同时,由于跳跃机器人可以轻松地越过数倍于自身尺寸的障碍物,这使得它在面对不平整地形上能发挥出更大的优势。因而,跳跃机器人逐渐进入机械设计领域研究者们的视野中,现已成为机械设计研究的热门领域之一。
蚱蜢、蝗虫、跳蚤、袋鼠、松鼠等生物因表现出了优秀的运动性能,都可以被作为跳跃机器人的仿生对象。如陈东良等[2]通过研究蝗虫的后腿结构特性,以具有仿生特性的四连杆结构模拟蝗虫的后腿结构,以弹簧为储能结构,设计出仿蝗虫跳跃机器人。实验测得该机器人具有良好的跳跃性能,其跳跃高度可达20 cm,跳跃距离可达80 cm。倪虹等[3]基于蝗虫的跳跃性能和力学特性,设计出以六连杆结构为腿部机构的仿生跳跃机器人。实验测得该机器人的跳跃高度能达到自身高度的129%。王欣等[4]通过对蝗虫的生理结构进行分析,采用双摇杆机构模拟蝗虫后腿结构,并且通过优化算法对其结构进行了优化。国立首尔大学研制的仿跳蚤跳跃机器人,利用记忆合金模拟跳蚤的后腿肌肉伸缩过程,并且以四连杆结构为基础设计出机器人的后腿机构。该跳跃机器人的质量仅为1.1 g,身长2 cm,却可以实现相当于自身30 倍的跳跃高度[5]。加州大学伯克利分校科研人员以平面八连杆机构为基础,结合串联弹簧驱动器,研制出了平均每隔0.58 s 便可以实现一次跳跃的机器人Salto[6-7]。王永健等[8]通过对松鼠的生理结构和运动机理进行研究,并且基于柔性脚趾设计出一种松鼠腿部跳跃机构,最后以实验证明了该机构能有效地模拟松鼠的跳跃特性。然而在大自然之中,与其他仿生对象相比,蚱蜢的跳跃性能更为优异,其跳跃距离能达到自身长度的15~30 倍[9-10]。加之蚱蜢在空中可以通过翅膀调整姿态,并且落地时的缓冲性能良好,因而成为了众多学者的研究对象。
本研究拟以蚱蜢为仿生研究对象,通过分析蚱蜢运动机理和后足的生理结构,仿生设计一种具有高爆发和出色的跳跃性能的腿部跳跃机构,然后对跳跃机构进行简化,根据运动学分析方法建立蚱蜢跳跃运动模型,并且从动力学和运动学的角度对模型进行分析与计算。最后,通过ADAMS 虚拟样机,对设计的跳跃机构进行仿真实验,以证明其在爆发性和跳跃性能方面的优越性。
2 蚱蜢跳跃机构模型的建立
2.1 蚱蜢腿部结构与运动机理
蚱蜢与自然界中大多数能够跳跃的生物类似,起跳的能量主要由发达的后足肌肉收缩提供。腿节、胫节、跗足3 部分构成蚱蜢的后足,其中跗足起稳定和支撑躯体的作用,并通过跗关节与胫节连接,腿节通过膝关节与胫节连接,通过肌腱的伸缩拉动胫节绕膝关节转动,腿节通过髋关节与身体相连。蚱蜢后足的结构如图1 所示[11]。
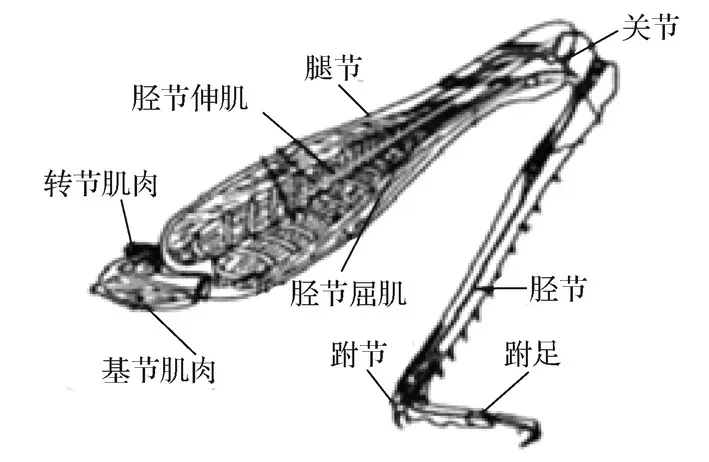
图1 蚱蜢后足的生物结构模型Fig.1 Biological structure model of grasshopper hind feet
胫节伸肌和胫节屈肌是蚱蜢后足肌肉的主要组成部分,其相互配合,使胫节绕关节向腿节方向转动,从而完成蚱蜢的起跳过程。已有研究结果表明,在蚱蜢的后足膝关节处有一个与弹簧相似的半月板结构,蚱蜢在起跳前依靠腿节的肌肉收缩带动半月板,在起跳瞬间释放出半月板中积蓄的能量,让胫节快速后摆,完成起跳动作。图2 所示为一个完整的蚱蜢起跳过程示意图。
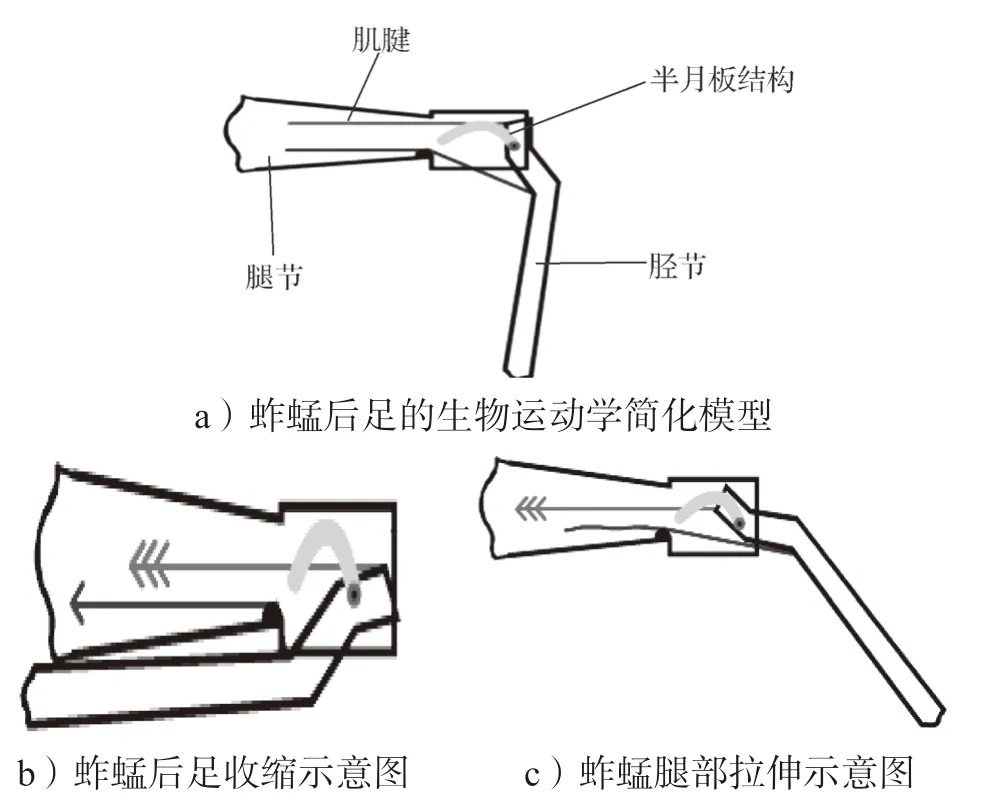
图2 蚱蜢起跳阶段后足运动示意图Fig.2 Schematic diagram of the hind foot movement of the grasshopper in the take-off phase
2.2 蚱蜢跳跃机构建模
基于对蚱蜢生理结构和运动机理的分析,仿生设计了蚱蜢后足机构模型,如图3 所示。蚱蜢跳跃机构模型主要包括4 部分:弹簧装置、减震系统、三连杆和曲柄滑块结构。在起跳阶段,通过拉动曲柄滑块结构使弹簧装置蓄力,并拉动胫节完成蓄力阶段,随后释放弹簧,依靠弹簧的瞬间释放使模型对地面产生极大的作用力,从而使模型获得最大的起跳速度。在落地阶段,通过减震系统,缓冲对地面的冲击力,并且为第二次起跳积蓄能量。
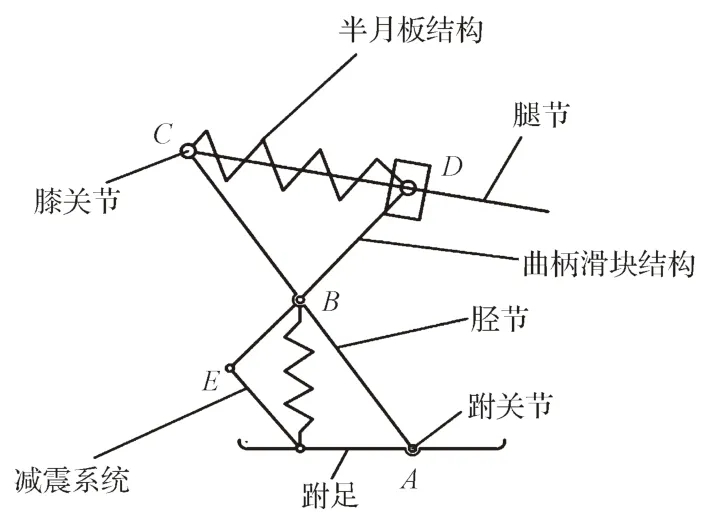
图3 蚱蜢跳跃机构模型示意图Fig.3 Schematic diagram of grasshopper jumping mechanism model
3 跳跃机构的建模分析
3.1 运动学建模与分析
对所设计的蚱蜢腿部跳跃机构模型进行简化,将各关节简化为自由度为1 的转动副。l1绕固定点O转动,l1和l2绕跗关节点A 转动,l2和l3绕膝关节点B 转动,l3和l4绕髋关节点C 转动。采用运动学分析方法[12]建立如图4 所示的运动学模型,其中X0-Y0是基坐标系,l1、l2、l3、l4分别为跗足、胫节、腿节、躯体。θ1、θ2、θ3、θ4分别为跗足与地面夹角、跗足角、膝关节脚、髋关节角。
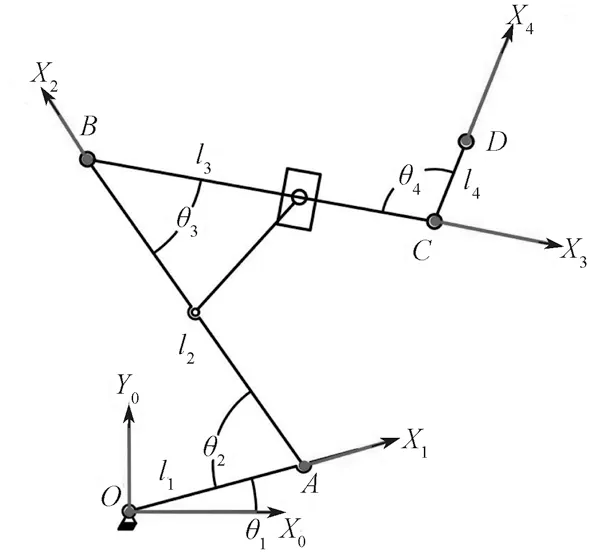
图4 蚱蜢腿部机构运动模型简图Fig.4 Sketch of the movement model of the grasshopper leg mechanism
两相邻连杆之间的齐次变换矩阵如下:
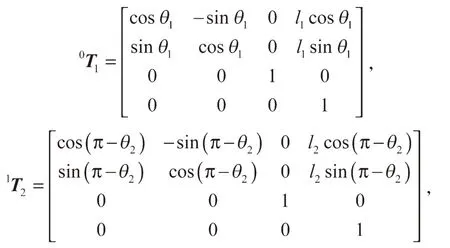
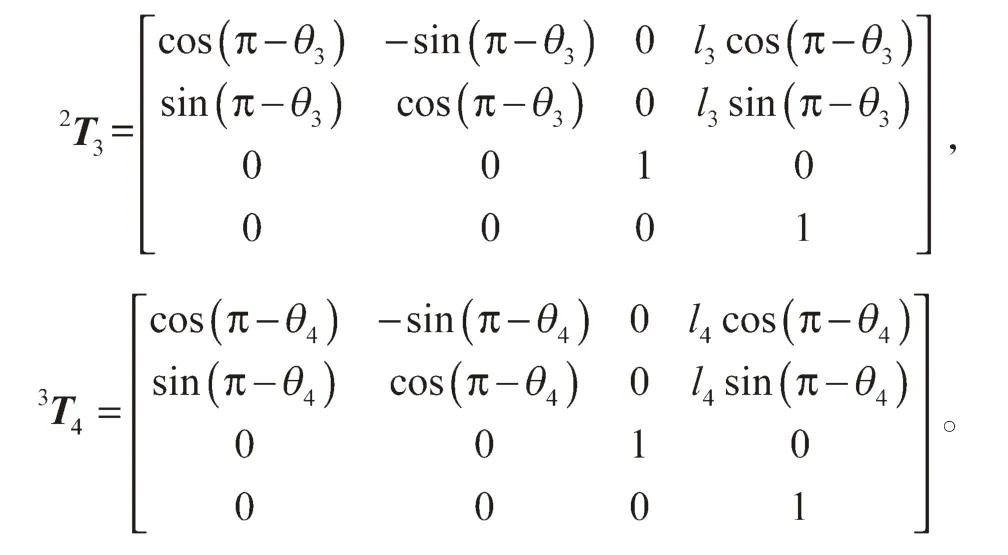
机器人各关节关于基坐标系OX0Y0Z0的位姿可由下式计算得:
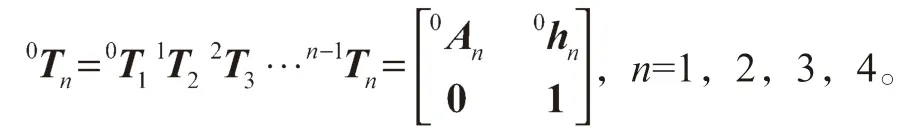
式中:0An为关节坐标系相对于X0-Y0坐标系的旋转矩阵;0hn为各关节坐标系相对于X0-Y0坐标系的位移矢量;0、1 均为分块矩阵。
髋关节的变换矩阵为
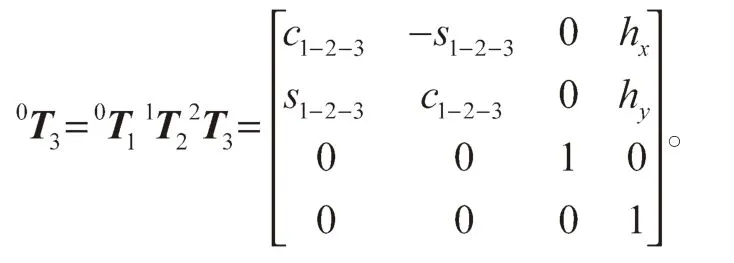
式中(hx,hy)为髋关节的位置坐标,且

将蚱蜢腿部关节角度的离散数值[13]通过Matlab进行多项式曲线拟合后,得到如图5 所示的各关节角度变化规律曲线。
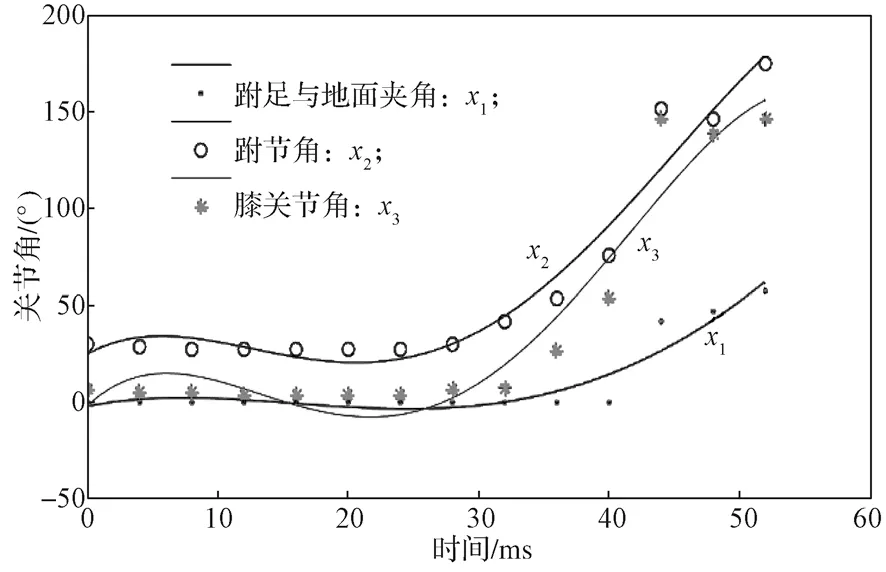
图5 蚱蜢起跳阶段关节角度变化规律曲线Fig.5 Regular curves of the joint angle change of grasshopper during the take-off phase
将图5 中蚱蜢起跳阶段的各关节角度和表1[14]所示蚱蜢的腿部尺寸代入机构运动学表达式(1)中。基于Matlab 对表达式进行编程计算,得到起跳阶段蚱蜢腿部关节在X 方向和Y 方向的位移变换曲线,如图6 所示。

表1 蚱蜢腿部尺寸Table 1 Grasshopper leg sizes mm
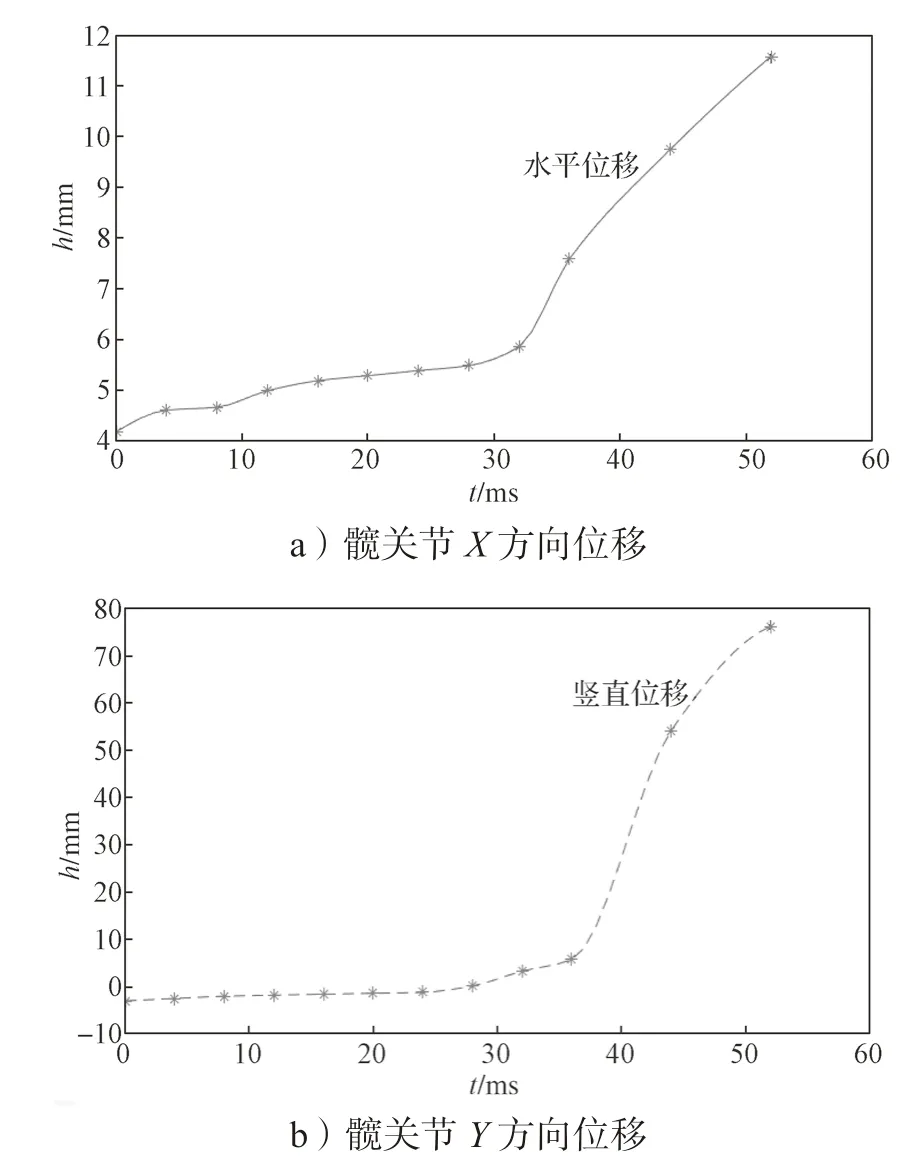
图6 髋关节位移曲线Fig.6 Hip joint displacement curve
把蚱蜢仿真中得到的髋关节的数据与图6 进行对比分析,发现两者的曲线变化趋势基本上一致,这表明模型在运动学方面的分析是正确的。
在跳跃机器人的研究中,发现影响跳跃机器人弹跳性能的主要因素为弹跳高度和起跳速度。因此从运动学角度上来说,微分分析对于弹跳机构的研究也是必不可少的。在机器人学中,利用雅可比矩阵对跳跃机器人进行微分运动求解是最常用的手段之一,一般采用雅可比矩阵把关节速度和机构末端的笛卡尔速度关联起来[14],即
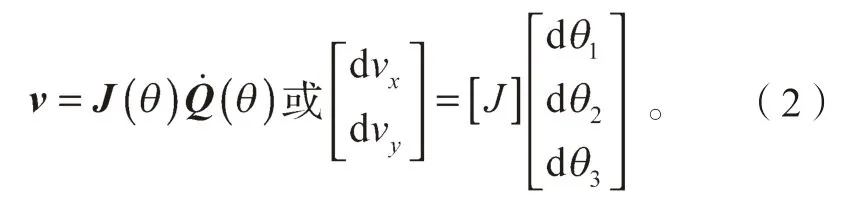
为了表明仿蚱蜢跳跃机构的运动学特性,课题组选取髋关节为对象进行研究,通过Matlab 对机器人起跳阶段的运动学进行数值计算,然后分析髋关节在起跳阶段的速度变化。数值计算步骤如下:采用最小二乘拟合方法对图6 中的关节角度数据进行处理,得到各关节的运动函数,将运动函数进行微分求解,得到角速度;其次,由髋关节的变换矩阵,得到雅可比矩阵J(θ);最后,把身体参数代入前文研究成果中,通过Matlab 对表达式(2)进行编程求解。图7 是求解所得的髋关节在起跳阶段的速度曲线图。
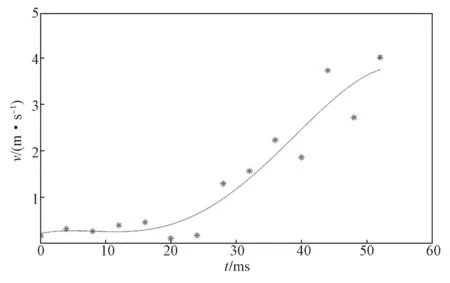
图7 起跳阶段髋关节速度曲线Fig.7 Hip joint velocity curve during the take-off phase
由图7 可以看出,一个完整的起跳过程可以分为两个阶段:起跳前期(0~28 ms),此阶段髋关节速度变化不明显,主要是腿节肌肉的蓄力。起跳后期(28~52 ms),在伸肌和屈肌的共同作用下,各骨骼关节快速展开,膝关节半月板中存储的能量迅速释放,让髋关节速度快速增大,进而以最大的起跳速度离开地面。
将图7 所示起跳阶段速度与髋关节起跳阶段仿真结果(如图8 所示)进行对比,发现两者的变化趋势大体上一致,从而证明了所建立的仿蚱蜢腿部结构模型的合理性与可行性。
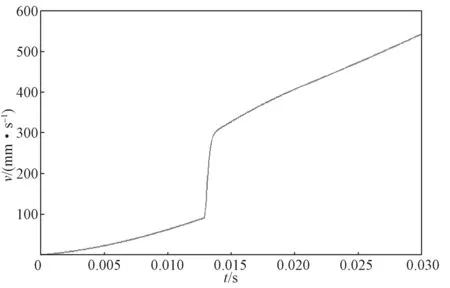
图8 起跳阶段髋关节速度仿真曲线Fig.8 Hip joint velocity simulation curve during the take-off phase
3.2 动力学建模与分析
从能量的角度对动力学分析是拉格朗日方程的优点之一。拉格朗日方程的建立是基于对模型的动能和势能的求解,再对其进行微分求解,可以获得各关节的输出力矩。根据拉格朗日方程,由模型的运动学模型建立蚱蜢后腿的动力学模型,如图9 所示,其中弹簧装置和滑块没有画出。
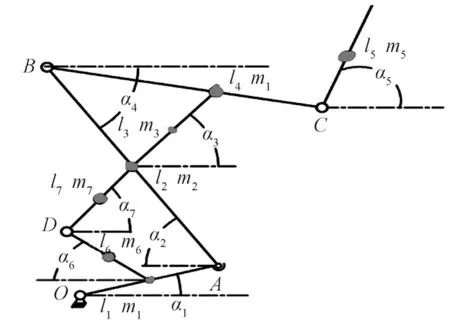
图9 蚱蜢腿部机构动力学模型Fig.9 Dynamics model of grasshopper leg mechanism
重新定义模型的各关节角度,有利于拉格朗日方程的导出,则进行如下定义:
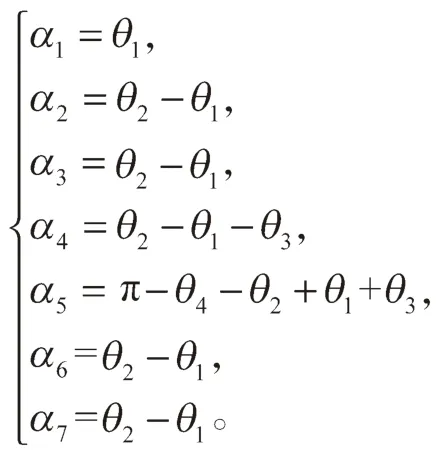
系统的总动能T 由如下两部分组成:连杆质心角速度产生的动能Ek和连杆质心线速度产生的动能Ep,即
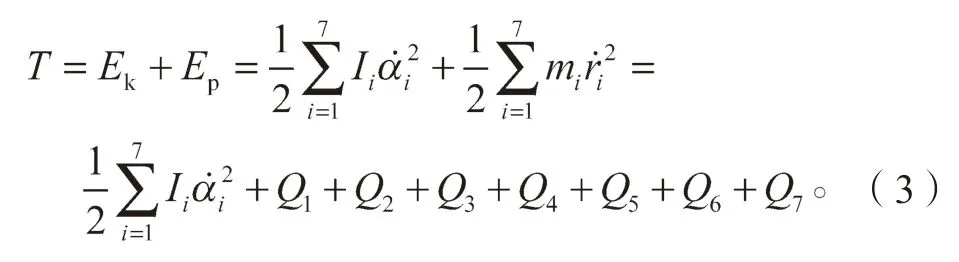
式中:mi为各连杆的质量;为各连杆的质心速度,且为各连杆的质心转动惯量;为各关节的转动角速度;Q1~Q7分别代表各杆件的平动动能,且
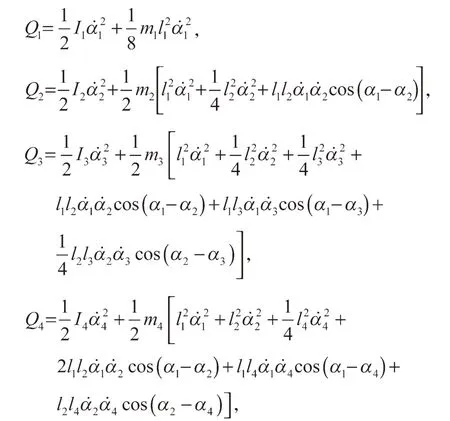
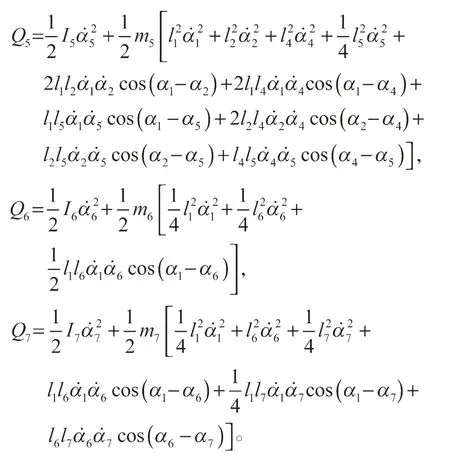
以机构跗足与大地接触点O 点为零势能点,系统的总势能G 由各杆件的重力势能和弹簧的弹性势能Ps组成,令储能弹簧弹性系数为K1,减震弹簧弹性系数为K2,求得系统势能为
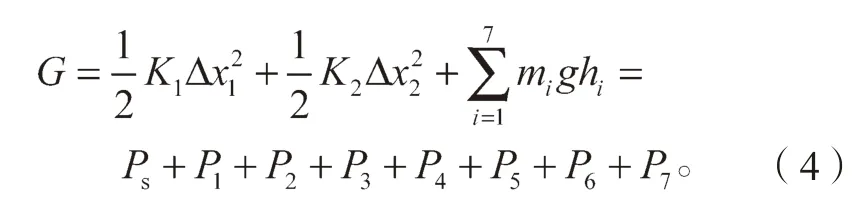
式中:Δx1、Δx2分别为两弹簧的形变量;g 为重力加速度;hi为各连杆质心垂直坐标位置;K1为储能弹簧弹性系数;K2为减震弹簧弹性系数;P1~P7分别代表各杆件的重力势能,且
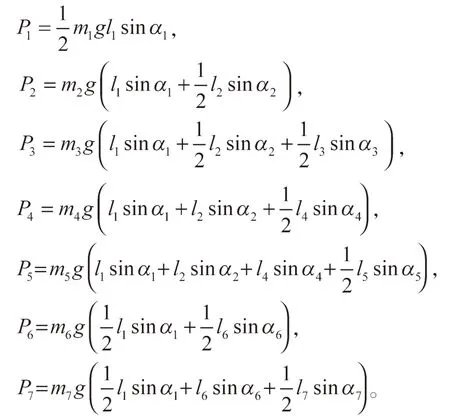
则拉格朗日函数如下式所示:

将动能方程(3)与势能方程(4)代入式(5)中,并做微分处理,得到各关节的输出力矩,为
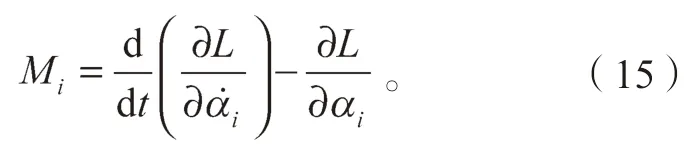
4 腿部机构动力学仿真分析
利用虚拟样机软件ADAMS 对三维模型进行仿真和验证[15],在仿真过程中,将所有杆件假设为刚性结构,且在运动过程中不存在变形。仿真模型将跗足、胫节和腿节分别设置为5, 25, 27 mm。在虚拟样机软件中,通过观察模型跳跃运动轨迹得到如图10所示的仿真跳跃动态变化图,将其与实验现象对比,可发现其基本符合蚱蜢后足跳跃过程。
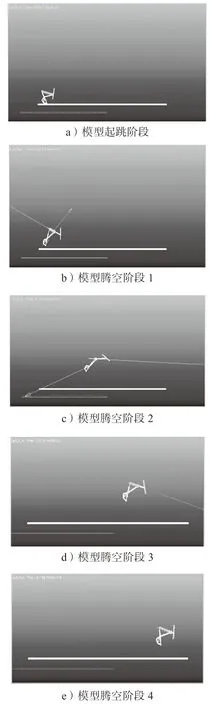
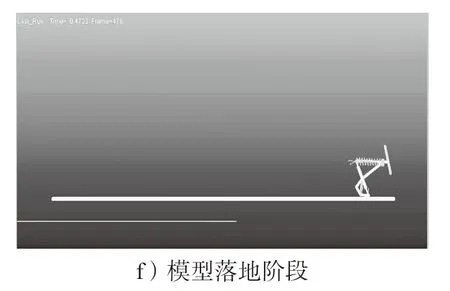
图10 模型仿真跳跃动态变化图Fig.10 Simulation jumping dynamic diagram of the model
图11 所示为通过仿真结果分析得到的质心位移变换图,从图中可以看出,在0~0.050 s 内,模型处于起跳阶段,此时模型水平、竖直位移增长速度较为缓慢。在0.050~0.472 s 内,机器人处于腾空阶段,在此阶段机器人的水平位移不断增大,竖直位移先快速增大,并在0.240 s 达到最大跳跃高度,然后减小。0.472 s 为模型抵达地面的时间。在整个跳跃过程中,位移曲线较为平滑,说明在跳跃过程中机构模型稳定性较好,且没有发生翻转现象。跳跃机构的最大跳跃距离约为1.84 m,最大跳跃高度约为31.5 cm,这一过程基本与蚱蜢的跳跃特性相似,因而证明了所设计模型的合理性。
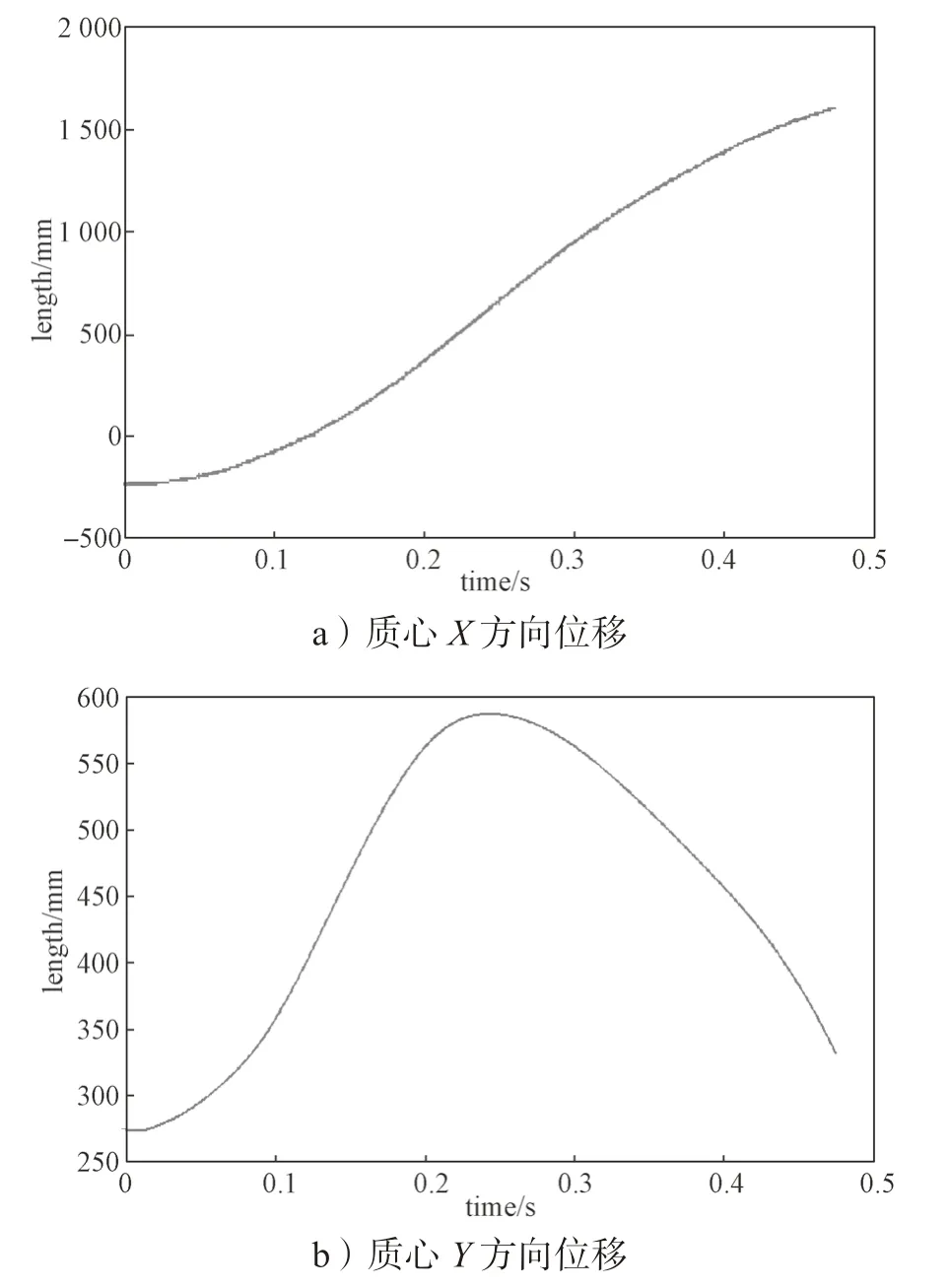
图11 质心位移变换仿真曲线Fig.11 Simulation curves of centroid displacement transformation
图12 为质心X 方向和Y 方向的速度变化曲线图,从图中可以看出,在0~0.05 s 内,模型质心Y 方向速度发生突变,且在极短的时间内迅速上升,体现了模型在起跳阶段的爆发性和突然性。模型Y 方向速度在0.14 s 时达到峰值,其后开始呈下降趋势,并且在0.24 s 减小到0 mm/s。0.240 ~0.472 s 为模型落地阶段,在这个阶段模型速度变化较为平稳,没有出现较大的波动,说明在落地阶段模型的稳定性较好,这为模型进行连续跳跃提供了基础。
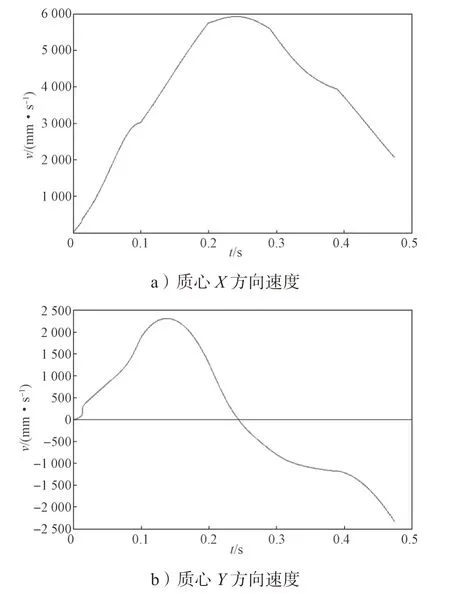
图12 质心速度变化仿真曲线Fig.12 Simulation curve of centroid velocity change
图13 是质心X 方向和Y 方向的加速度曲线,其中0~0.05 s 为模型起跳到离开地面阶段。由图可知,加速度在0~0.05 s 内产生突变,这是由于模型膝关节中弹簧存储的能量被迅速释放所引起的,体现了模型在起跳阶段的爆发性。
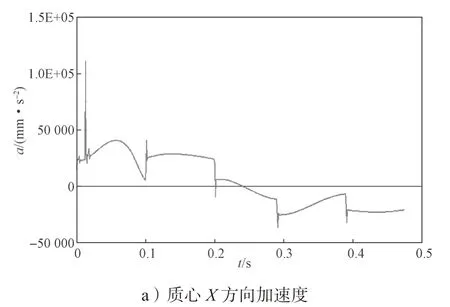
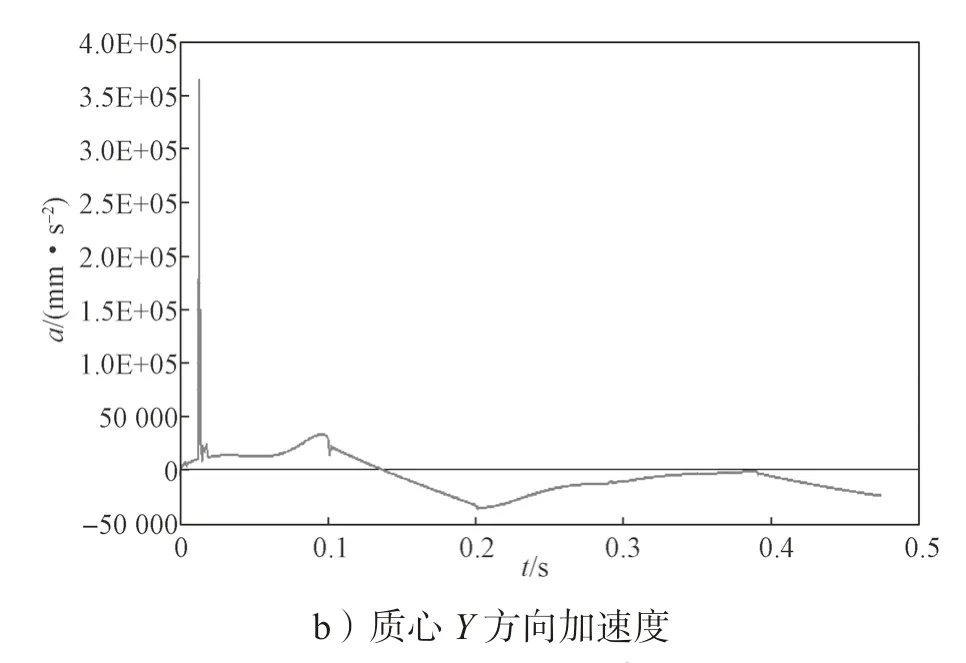
图13 质心加速度仿真曲线Fig.13 Centroid acceleration simulation curve
图14 为有减震系统跗关节受力图和无减震系统跗关节受力图,0.472 s 为模型抵达地面时间。从图中可以看出,当模型抵达地面瞬间,跗关节受到极大的地面冲击力,而减震系统可以减轻一半以上的对跗关节的地面冲击力,从而使模型落地更为平稳,这一结果证明了此模型具有优越的跳跃性能。
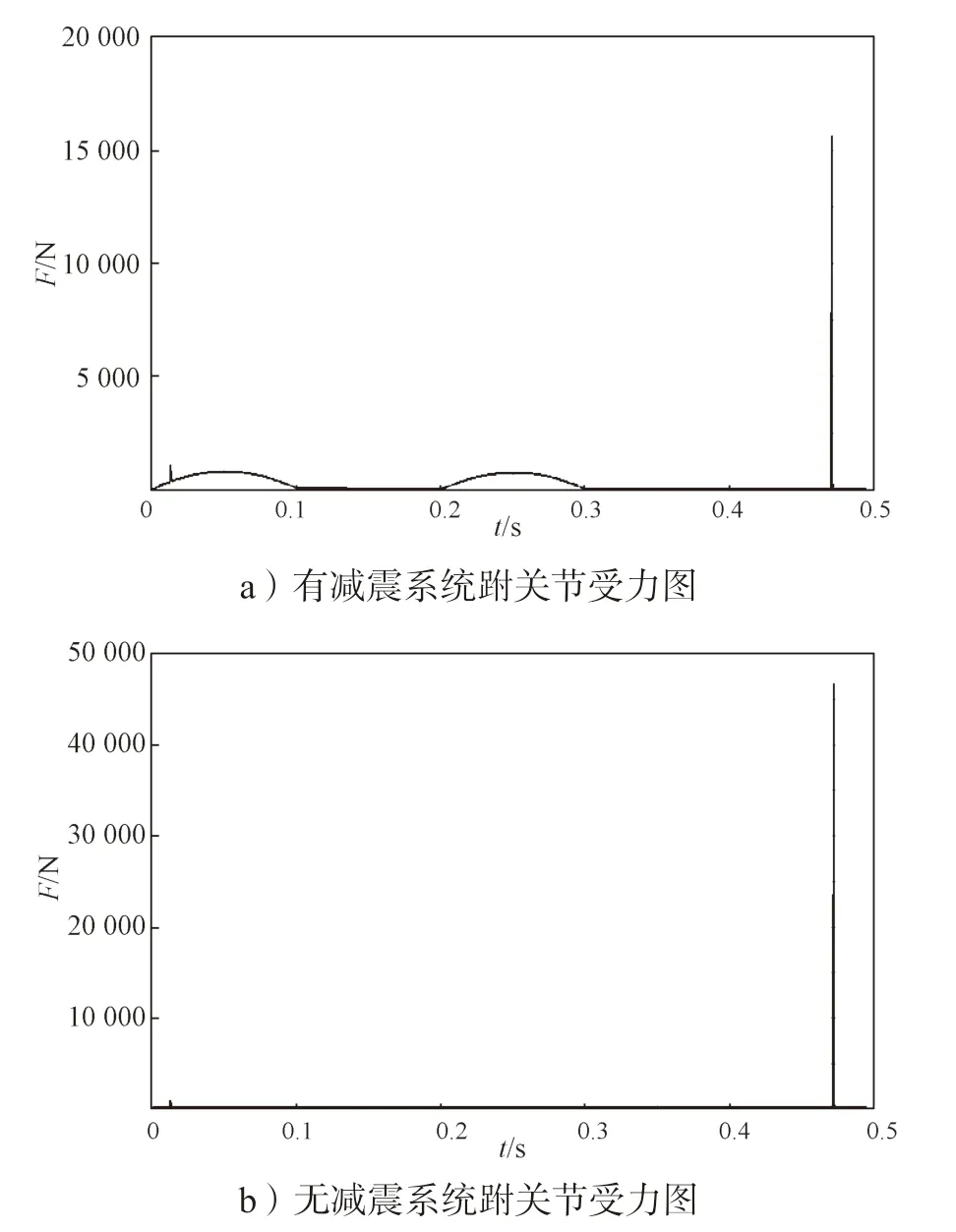
图14 跗关节受力图Fig.14 Tarsal joint force diagram
5 结语
本研究分析了蚱蜢腿部结构组成,并以曲柄滑块结构模拟蚱蜢腿部肌腱、以弹簧装置模拟腿部膝关节的半月板结构,仿生设计出仿蚱蜢跳跃机器人的腿部结构模型。对模型进行运动学分析,并通过Matlab数值计算,得到蚱蜢起跳阶段髋关节位移和速度曲线,与ADAMS 仿真实验结果进行对比,发现两者的变化趋势大体一致,证明了所设计的仿蚱蜢腿部跳跃机构模型的合理性和可行性。研究结果也表明:在ADAMS 仿真实验中,机构模型的跳跃距离可达到1.84 m,跳跃高度可达31.5 cm,基本与蚱蜢的运动特性相似,且在跳跃过程中,模型稳定性能较好,并未有翻转现象发生,表明模型机构具有优异的跳跃性能。在起跳阶段起跳速度发生突变,体现了模型在起跳阶段的爆发性和突然性。
本文通过对蚱蜢生理结构和运动机理进行研究分析,设计了蚱蜢腿部跳跃结构模型,为进一步对结构进行优化奠定了基础。

