橡胶砂力学性能的三维离散元数值模拟

彭庆奉，刘方成，陈 翔

（湖南工业大学 土木工程学院，湖南 株洲 412007）

1 研究背景

随着国民经济的快速发展、汽车数量的持续增长，人类在享受经济发展的成果时，不得不面对日益增多的废旧橡胶轮胎问题。由废旧轮胎颗粒与天然土按预定比例配合得到的橡胶-土混合料（参与混合的土通常采用性质稳定的天然砂，故一般简称橡胶砂），具有密度低、弹性变形能力强、耗能大、剪切模量低等特点，已被广泛应用于轻质回填、公路路基、边坡、挡土墙、沥青路面和道路建设中[1-5]。因而，正确地掌握废旧轮胎与土体混合物的力学特性是该类工程应用的关键。

目前，纵观国内外已有研究成果，橡胶砂的力学特性主要受橡胶特性（含量、尺寸和形状）和砂特性（即密度、颗粒形状和粒度级配）的影响。如：J.G.Zornberg 等[6]考虑了最佳轮胎橡胶含量、轮胎切片的长宽比、砂的相对密度以及围压对试样特性的影响等影响因素，指出混合物的强度取决于两方面的因素，一是轮胎切片与砂的内部剪切机制，另外就是轮胎切片的加固作用。M.Ghazavi 等[7]对3 种碎料含量、3 种碎料宽度和给定宽度的不同长宽比进行了大型直剪试验，研究了胎屑长宽比对砂土抗剪强度特性的影响。T.B.Edil 等[8]的研究结果表明，轮胎碎屑砂混合料的强度高于纯砂的。同时，密度较高的砂胎材料（rubber sand mixture，RSM）比密度较低的砂胎材料具有更强的抗剪强度。此外，当轮胎碎片体积分数为10%时，与纯砂相比，在低、中载荷下具有更大的抗剪强度。一些学者也进行了数值模拟以研究橡胶砂的力学行为，尤其是用P.A.Cundall 等[9]提出了以离散元数值分析法分析颗粒材料的不同力学性质，如颗粒体的本构关系、细观力学特性及位移变形特性等。Lee J.H.等[3]采用有限元方法对废旧轮胎碎片作为挡土墙回填土进行了有限元模拟，并与现场数据进行了比较，得出橡胶与砂土可以有效地用作回填材料的结论。国外最早由J.R.Valdes 等[10]用离散单元法（discrete element method，DEM）模拟纯轮胎和砂土混合料，他们将每个橡胶颗粒模拟为一个圆盘，其剪切模量和摩擦系数随接触重叠而变化，该模型虽然能够表示加载-卸载滞后，但是忽略了残余应变。Lee C.等[11]采用二维离散元方法研究了不同体积分数的颗粒在不同应变水平下的行为。J.C.Lopera Perez 等[12]对不同橡胶含量的试样进行同位素约束和剪切，使用球形粒子和赫兹接触模型进行了三维模拟，在两种不同材料接触的情况下，用平均刚度计算接触力。还研究了橡胶砂在大应变下的液化[13]和临界状态[14]，虽然他们的结果在定性上与文献中发现的实验结果一致，但缺少对不同混合物进行严格地定量比较。Li W.等[15]开展了橡胶砂的三轴试验，从微观到宏观研究了掺入不同类型基质砂的橡胶的力学行为。Wang C.等[16]对橡胶砂在直剪试验下进行三维数值模拟，结果表明，添加橡胶颗粒后，提高了混合物的应变硬化特性和剪切延性。Gong L.X.等[17]采用离散单元法对含大颗粒橡胶颗粒的RSM 三轴试验进行了数值模拟，分析了不同橡胶含量的RSM 的宏观行为和相应的微观力学响应。M.Asadi 等[18]利用YADE 平台对橡胶砂进行了三轴试验模拟，结果表明，随着橡胶含量的增加，橡胶砂的抗剪强度降低。刘方成等[19]通过颗粒流软件，对不同工况下的橡胶砂进行了一系列双轴压缩离散元模拟试验，考虑了不同含量与粒径对橡胶砂力学行为的影响。闫欣宜等[20]开展了橡胶纤维－砂不同配比的三轴剪切试验，并与室内试验结果进行了比较。

橡胶与砂自身的材料特性及胶砂混合体内部结构特征是控制橡胶砂强度和变形性质的主要因素。但已有研究中对于橡胶砂的微观变形机理研究较少，因此本文通过颗粒流软件，对橡胶砂混合料进行三维三轴压缩模拟试验，从宏观、微观两方面分析配比、粒径比和围压对橡胶砂力学及变形特性等的影响，为橡胶砂的实际工程应用及后续研究提供参考。

2 橡胶砂三轴压缩的PFC3D 模拟

2.1 PFC3D 三轴压缩试验

用PFC3D模拟三轴压缩试验时，模拟橡胶砂的大小颗粒装在由“墙体”模拟的容器中，定义圆柱边界墙和上下边界墙作为加载板，为防止颗粒溢出墙体，圆柱边界墙作为有限墙应当适当增加高度，因为后期加载试样会产生变形，试验示意图见图1。

图1 PFC3D 三轴压缩试验示意图Fig.1 Schematic diagram of PFC3D triaxial compression tests

2.2 PFC3D 模型的建立

本研究中试样高度为80 mm，直径为39.1 mm。本模型中砂颗粒的粒径范围为1.2～1.4 mm，平均粒径为1.33 mm。橡胶颗粒的平均粒径分别为0.8, 1.3,2.9 mm，即橡胶与砂的粒径比(D50r/D50s)考虑0.6,1.0, 2.2 共3 种情况。试验用橡胶颗粒和砂的级配曲线如图2 所示。

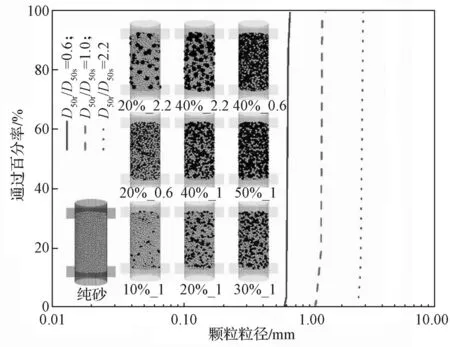
图2 颗粒级配曲线和数值模拟试样Fig.2 Particle gradation curves with numerical simulation samples

利用PFC3D可以根据需要建立不同级配的橡胶砂混合物，本研究中橡胶与砂颗粒直径服从均匀分布，模拟试样砂颗粒密度ρ砂颗粒=2.65 g/cm3，橡胶颗粒密度ρ橡胶颗粒=1.165 g/cm3，孔隙比e=0.4，试样内颗粒在计算范围内，符合计算标准。开展PFC3D数值模拟试验时，每种工况下混合物试样的颗粒总数为4 646～28 636 不等，通过伺服机制控制加载系统使数值模拟过程达到指定围压，采用应变控制的加载方式，当轴向应变达16%时停止加载并终止试验。随着胶－砂粒径比(D50r/D50s)增大，模型中橡胶颗粒数减少，砂颗粒数增多，图2 给出了最终生成的数值试样模型示意图。

2.3 橡胶砂接触模型及细观参数的选择

接触刚度模型是通过设定颗粒接触的法向割线刚度和切向切线刚度，从而将颗粒间的接触力与相对位移联系起来。本文采用线性接触刚度模型，橡胶砂细观参数选取借鉴文献[17]和[21]，具体参数见表1。橡胶砂试样中有3 种类型的接触。橡胶颗粒之间的接触、橡胶颗粒与砂基质之间的接触以及砂基质内部的接触，线性接触模型用于描述橡胶颗粒与接触处砂基质之间的相互作用，因为它在建模无黏性颗粒材料时简单有效，橡胶颗粒间的接触也采用了线性接触模型。为了模拟颗粒形状效应，减少计算量，将滚动阻力线性模型引入砂体中。

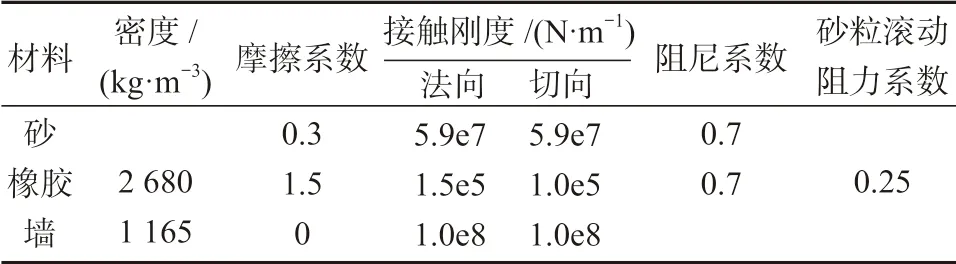
表1 橡胶砂细观参数Table 1 Microscopic parameters of the rubber sand

2.4 试验工况

分别在100, 200 kPa 围压下，对3 种粒径比、6种橡胶颗粒质量分数(以ω（橡胶）表示)的橡胶砂进行试验研究，试验工况如表2 所示。

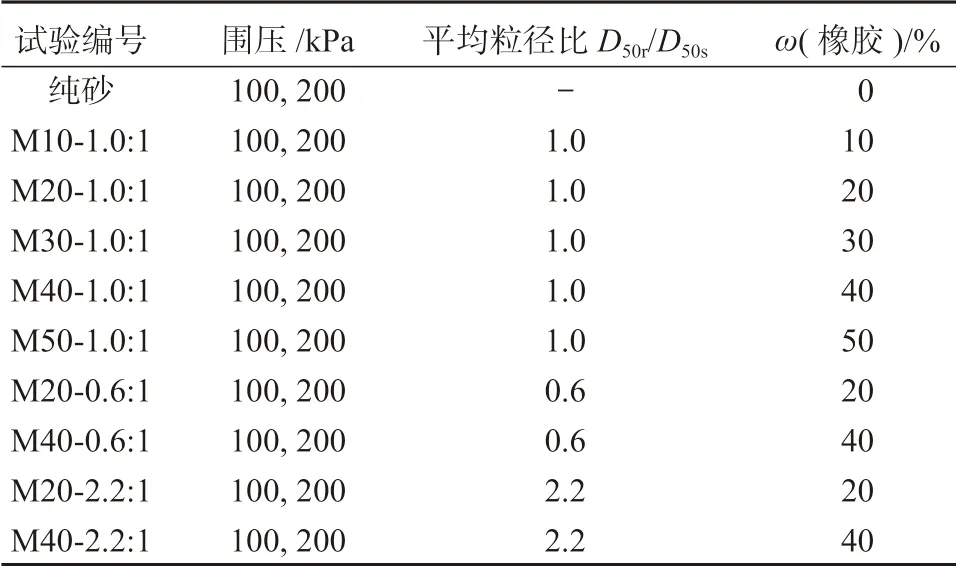
表2 试验工况Table 2 Test conditions

3 结果分析

3.1 试验值与PFC3D 模拟值对比

图3 为纯砂和ω(橡胶)=10%橡胶砂的偏应力-轴向应变的试验值和PFC3D模拟值对比[21]。

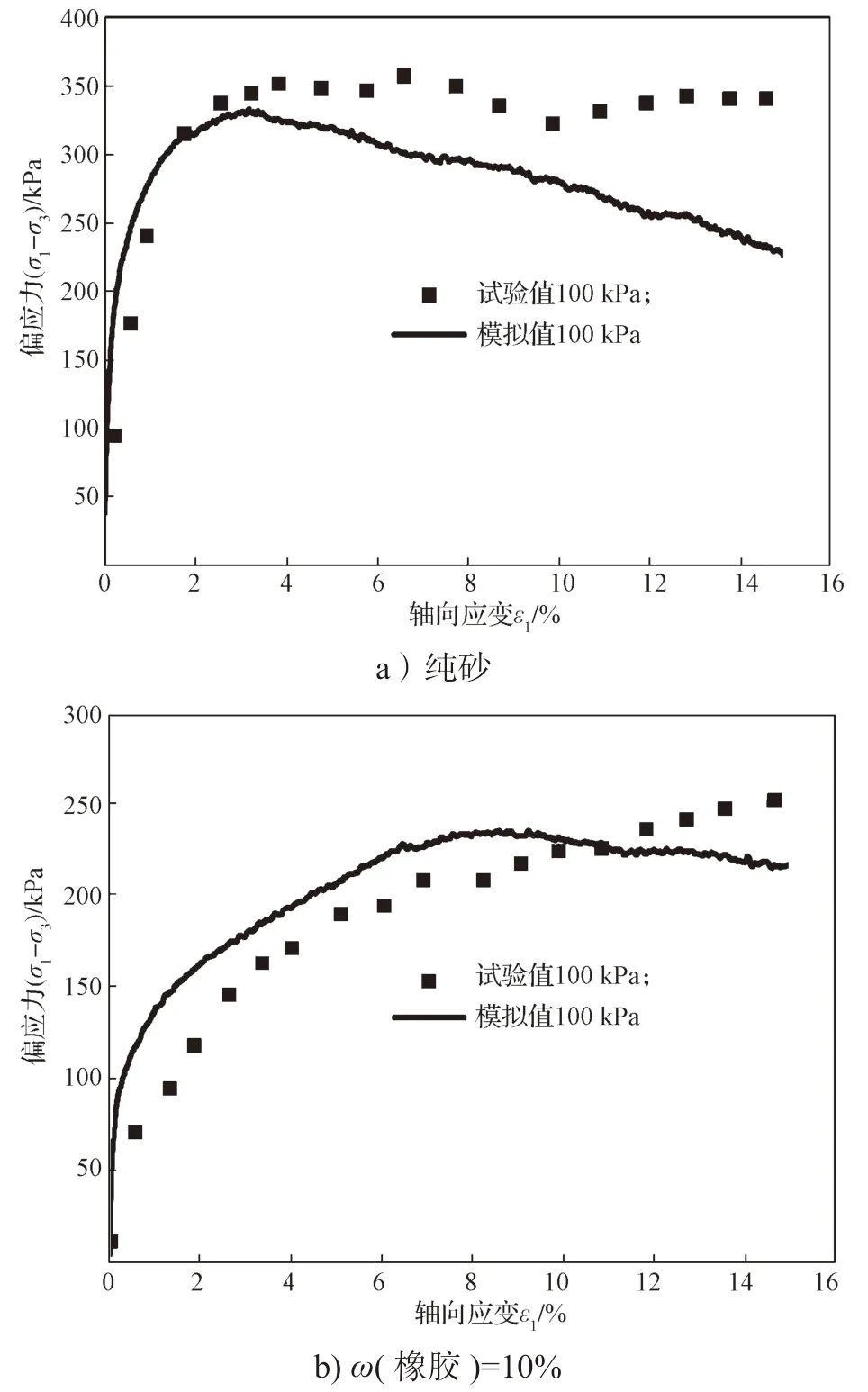
图3 纯砂和ω(橡胶)=10%橡胶砂的偏应力-轴向应变的试验值和PFC3D 模拟值对比Fig.3 Comparison of deviator stress-axial strain between experimentol values and PFC3D simulation value of pure sand and ω(rubber)10% rubber sand

对比图3 中的曲线可见，橡胶砂细观参数的选取对于后面开展的不同工况模拟试验具有一定的参考意义。

3.2 橡胶含量的影响

图4 为粒径比D50r/D50s=1.0，6 种不同橡胶含量橡胶砂在围压为100, 200 kPa 下的偏应力或体应变与轴向应变的关系曲线。由图4a、4c 所示不同试样的偏应力与轴向应变曲线可知：随着轴向应变增加，纯砂偏应力先是线性增加，随后进入非线性，出现应力峰值，其后进入应力软化下降段。随着橡胶含量的增加，偏应力的增加速率显著降低，显然，在砂样中加入橡胶颗粒会降低其整体刚度，橡胶-砂混合物的强度随着橡胶颗粒的加入而降低主要归因于软橡胶颗粒的加入。由图4b、4d 所示轴向应变与体积应变的关系曲线可知，纯砂试样表现为膨胀行为，ω(橡胶)=10%的样品显示5%应变的压缩行为，然后曲线开始上升，显示膨胀行为。在ω(橡胶)＜10%的样品中，膨胀行为更明显，而对于ω(橡胶)＞10%的样品，压缩行为更明显。因此，10%的样品可以作为砂状行为和橡胶状行为之间的边界。

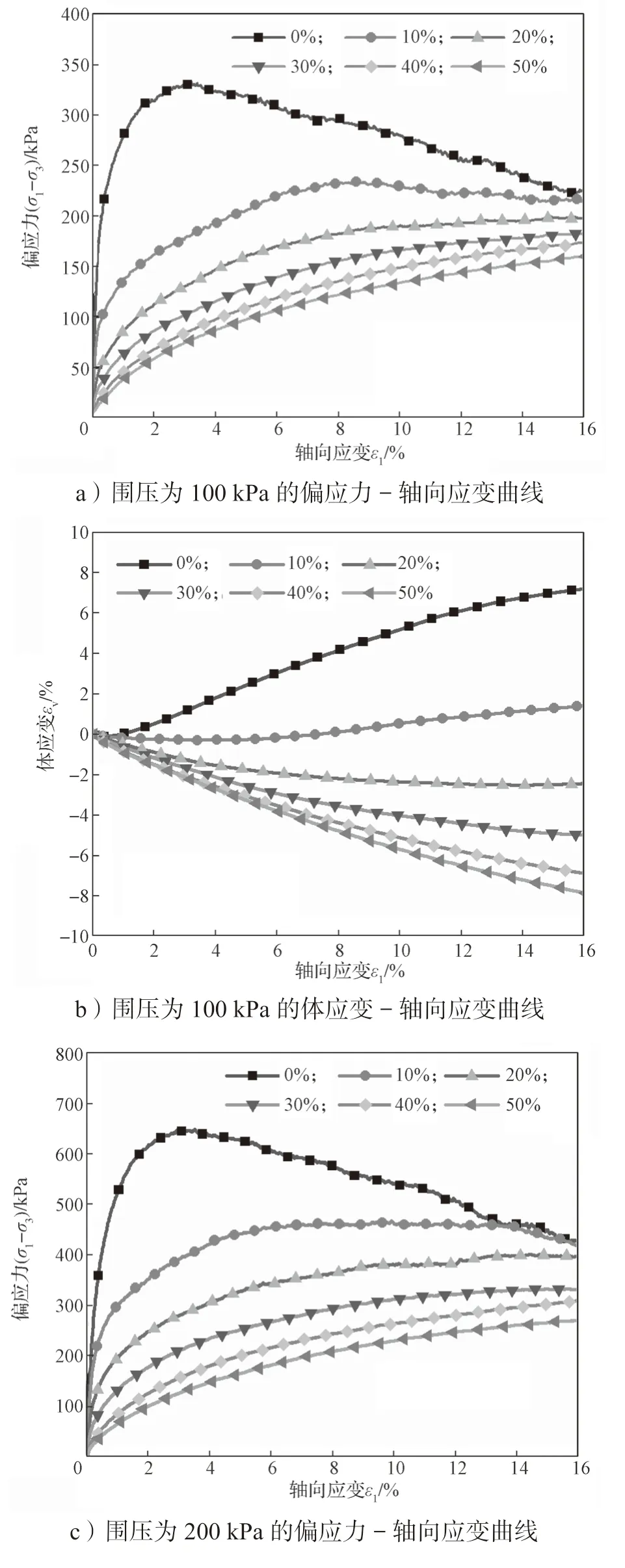
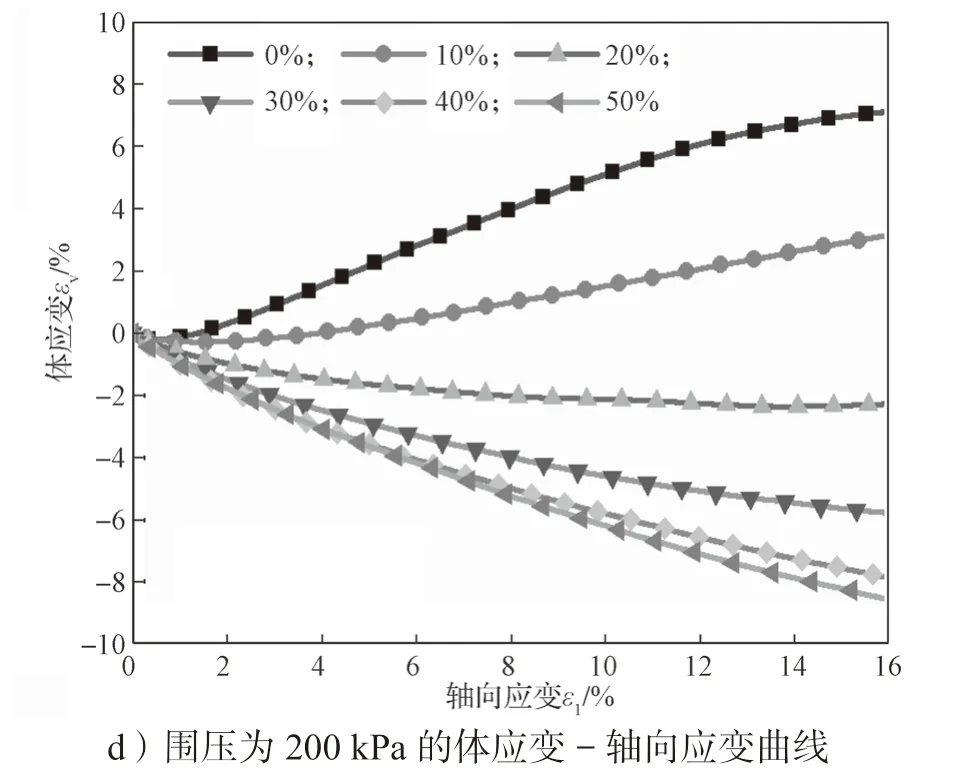
图4 D50r/D50s=1.0 下围压为100, 200 kPa 时不同橡胶含量橡胶砂的偏应力或体应变与轴向应变的关系曲线Fig.4 Relationship between deviator stress volume strain and axial strain of rubber sand with different rubber content when the confining pressure is 100 kPa and 200 kPa and the particle size ratio D50r/D50s=1.0

3.3 平均粒径比的影响

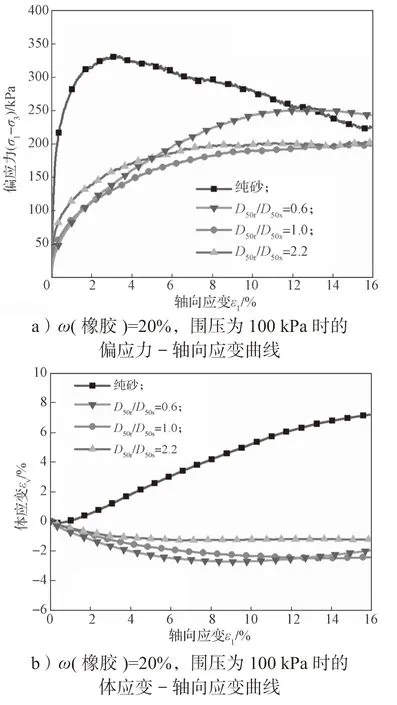
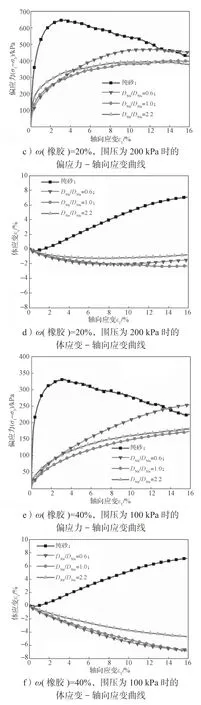
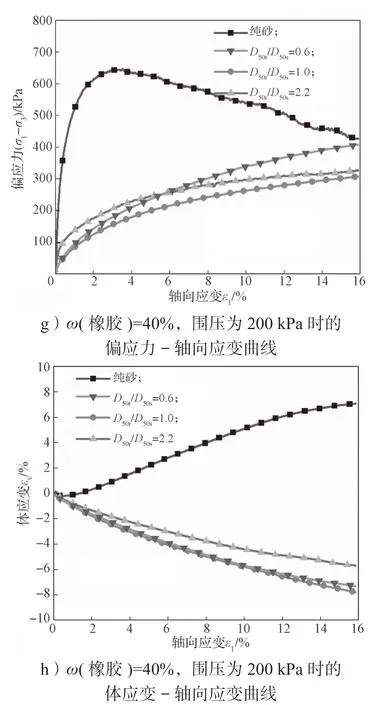
图5 围压为100, 200 kPa 时不同粒径比的不同橡胶含量橡胶砂偏应力或体应变与轴向应变的关系曲线Fig.5 Relationship between deviator stress, volume strain and axial strain at different particle size ratios when the confining pressure is 100 kPa and 200 kPa

图5 为不同粒径比时偏应力和体应变与轴向应变的关系曲线。由图可知ω(橡胶)=0（纯砂）时，偏应力－轴向应变关系试验曲线表现出明显的应变软化特征，其剪切体应变特性表现为：在剪切之初轻微剪缩，而后发生剪胀。ω(橡胶)=20%, 40%的橡胶砂应力－应变关系特性随粒径比的变化规律如下：当ω(橡胶)=20%，围压为100, 200 kPa 时，3 种粒径比的橡胶砂均未出现峰值，且D50r/D50s=0.6, 1.0, 2.2 的橡胶砂表现出由应变软化型向应变硬化型逐渐过渡的趋势。当ω(橡胶)=40%，围压为100, 200 kPa 时，3 种粒径比的橡胶砂均表现出近似线性的硬化型应力－应变关系，其中以D50r/D50s=0.6 的橡胶砂硬化型特性最为明显。

ω(橡胶)为20%, 40%的橡胶砂剪切体应变特性随粒径比的变化规律如下：当ω(橡胶)为20%时，D50r/D50s=0.6 的橡胶砂显示10%应变的压缩行为，然后曲线开始上升，显示膨胀。而D50r/D50s=1.0, 2.2 的橡胶砂未发生剪胀现象，但剪缩值较小。当ω(橡胶)=40%时，3 种粒径比橡胶砂均表现为持续发生剪缩，在该含量范围内，随着橡胶粒径的增加，橡胶砂的εv-εl曲线衰减速率变慢，且D50r/D50s越高，其εv-εl曲线斜率衰减速率越慢。

3.4 围压的影响

图6a～6d 显示了在100 kPa 和200 kPa 围压粒径比D50r/D50s=1.0，下排水三轴试验中纯砂和4 种橡胶砂试样的偏应力－应变曲线。随着围压的增加，低橡胶含量（ω(橡胶)≤10%）橡胶砂的膨胀反应逐渐受到抑制，应变软化减弱；橡胶砂试样的体应变曲线（图6e～6h）也可以使用PFC3D代码进行测量和记录。随着围压的增加，高橡胶含量（ω(橡胶)≥20%）橡胶砂的压缩性更明显，应变硬化特性增强，应力－应变曲线上升。

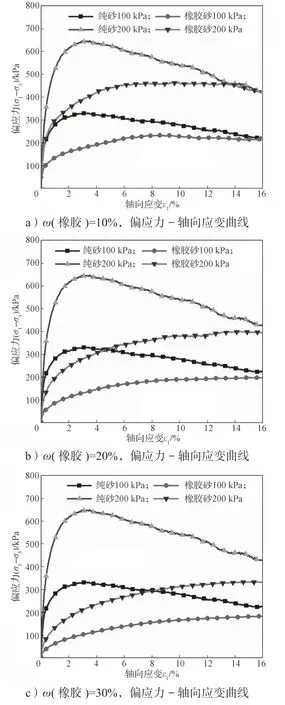
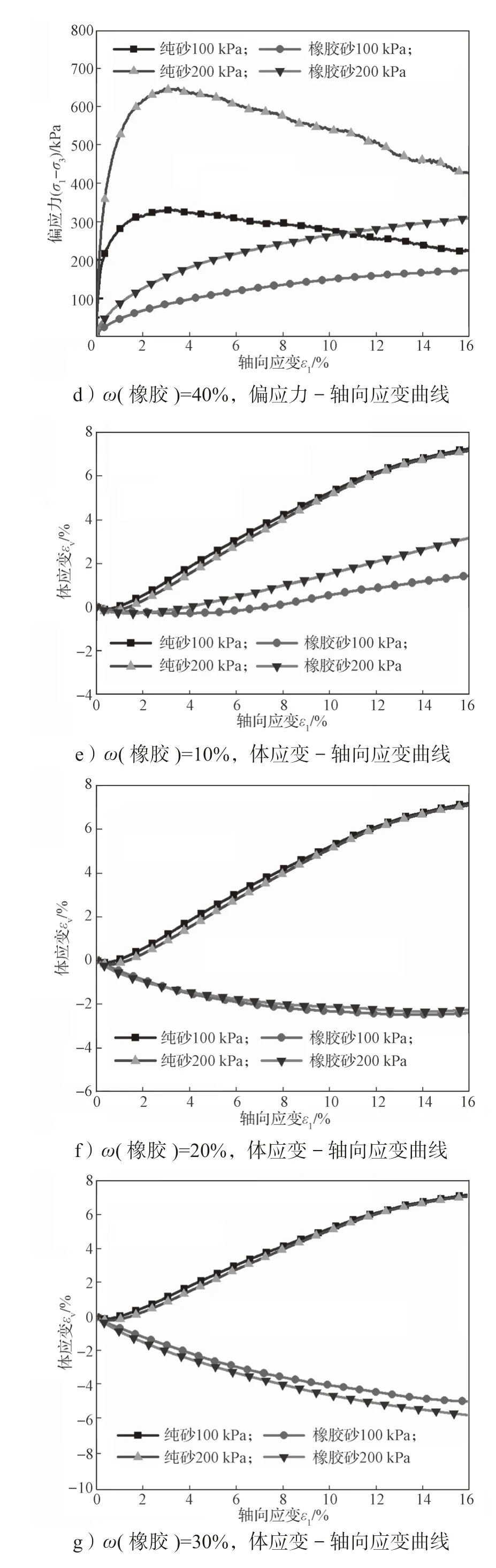
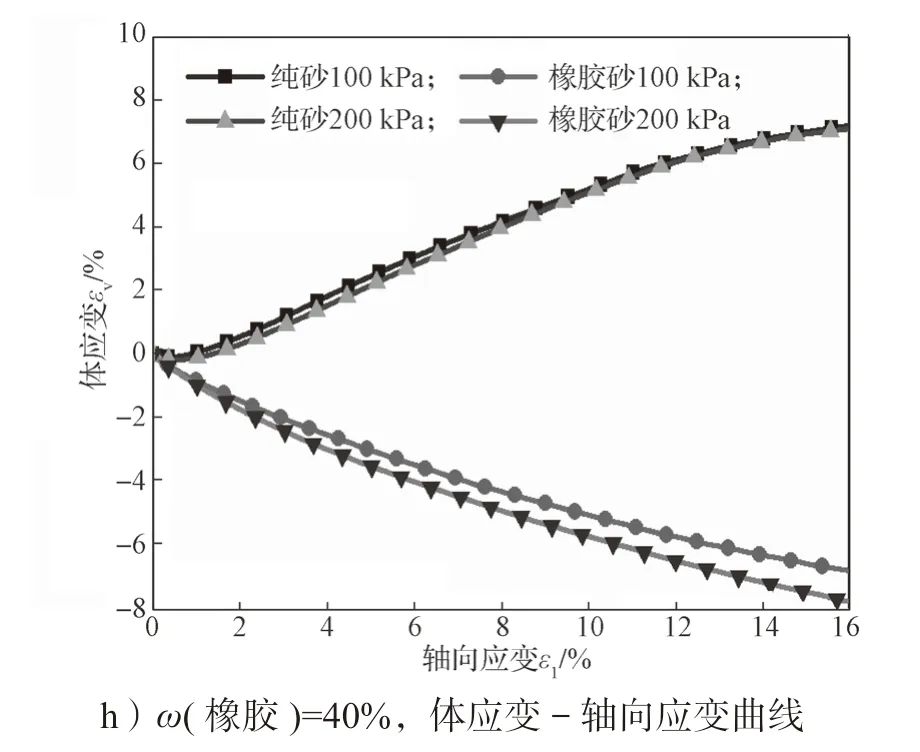
图6 纯砂与不同橡胶含量橡胶砂在不同围压、D50r/D50s=1.0 时偏应力或体应变与轴向应变的关系曲线Fig.6 Relationship between deviatoric stress or volume strain and axial strain under different confining pressures and the particle size ratio D50r/D50s=1.0 with pure sand and different rubber content

4 结论

当ω(橡胶)＜10%时，橡胶砂表现出类砂力学特性，即先剪缩后剪胀，应力-应变曲线呈软化型；当ω(橡胶)≥20%时，橡胶砂表现出类橡胶力学特性，试样单调剪缩，应力-应变曲线呈硬化型。随着橡胶含量的增加，橡胶砂应力应变曲线的峰值降低。

胶砂粒径比对橡胶砂应力-应变关系存在一定的影响，主要表现为随着平均粒径比的增大，体应变增大，应力-应变曲线降低，抗剪强度减小。

随着围压的增加，低橡胶含量的橡胶砂剪胀和应变软化特性得到抑制，高橡胶含量橡胶砂剪缩和应变硬化特性增强。混合料抗剪强度的降低主要归因于软橡胶颗粒的加入所引起的橡胶砂试样刚度损失，而其膨胀反应受到抑制的原因是橡胶颗粒容易被挤压而产生体积收缩。