徐变效应对大跨度悬臂浇筑拱桥施工阶段拱圈受力行为的影响
曹红亮, 王祺顺, 田仲初, 张祖军
(1.长沙市公路桥梁建设有限责任公司, 湖南 长沙 410004; 2.湖南省交通科学研究院有限公司, 湖南 长沙 410014;3.长沙理工大学 土木工程学院, 湖南 长沙 410015)
截面拉应力为悬臂浇筑拱桥的重要监控参数,它决定了拱圈悬臂浇筑过程中拱圈是否开裂、结构是否安全。传统的研究主要考虑拱圈自重、横隔板等其他外荷载作用对索力的影响,徐变效应影响方面的文献报告较少[1-2]。本文以某在建特大跨悬臂浇筑拱桥为研究对象,分析徐变效应对拱圈受力及变形的影响规律,该研究成果可为大跨径拱桥施工及安全控制提供借鉴,具有一定的工程意义。
1 工程概况
本工程为某在建特大跨悬臂浇筑拱桥,桥址位于贵州某水库区,设计荷载等级为公路-Ⅰ级,拱圈净跨径为240m,净矢高为40m,拱轴系数为1.85。拱圈截面使用C60混凝土,为单箱双室截面,宽10m,高4.5m,从拱脚至拱顶位置,顶板厚度由80cm变至35cm,腹板宽度由65cm变至35cm,底板厚度由50cm变至35cm,变化规律均为二次抛物线。拱桥沿桥梁纵向分为37个节段,两岸拱脚1#为支架现浇施工段,2#~18#节段采用斜拉扣挂悬臂浇筑施工工艺,拱顶合龙段使用吊架合龙[3]。桥型布置见图1,施工节段布置见图2。
2 徐变理论
目前徐变在工程界未形成统一的计算理论及方法,常用计算理论有:有效弹性模量法、老化理论、先天理论、混合理论等。这些理论均基于徐变-应力线弹性假设,且能满足叠加原理[4-5]。
根据前人研究成果及规范,混凝土强度低于设计强度50%时,徐变与应力呈线性正相关关系,若考虑任意时刻t0对结构施加一初应力σ,后继在不同时间间隔Δt内施加应力增量Δσ,则任意时刻总应变为:
(1)
式中:ε(t,τ0)表示τ0到t时刻混凝土总应变;σ0(τ0)为τ0时刻加载的混凝土应力;Δσ为应力增量,Δστi为加载至τi时刻混凝土应力变化量;E为混凝土弹性模量,φt,τ0为t时刻的徐变系数;εsht,τ0为t时刻徐变高阶应变量,一般可略去。

图1 桥型布置图(单位: cm)

图2 悬浇施工节段布置示意图
3 徐变理论在ANSYS中的实现
为简化计算,按线性徐变理论进行分析,目前在ANSYS中并没有专门模拟徐变的模块,可借鉴金属蠕变理论对混凝土徐变效应进行分析。根据金属蠕变理论,ANSYS中提供了显示积分计算与隐示积分计算2种模拟方式,相关研究表明:在施工阶段分析过程中,采用隐示计算方法可能会存在结果奇异[6-9],因此采用显示积分计算方法实现对徐变的模拟。
选取ANSYS中6号徐变方程作为徐变准则,同时采用应变强化准则以考虑应力随时间的变化情况,不考虑温度对徐变的影响。
ε=C1×σC2×tC3+1×e-C4 /T/(C3+1)
(2)

(3)
(4)
式中:C11表示第1个加载时刻内徐变系数;C1i表示加载至i时刻徐变系数。
在ANSYS中,假定单位步长内徐变系数为常数,同时取较小的时间步长以保证在徐变系数变化剧烈时的计算精度,具体流程如图3所示。
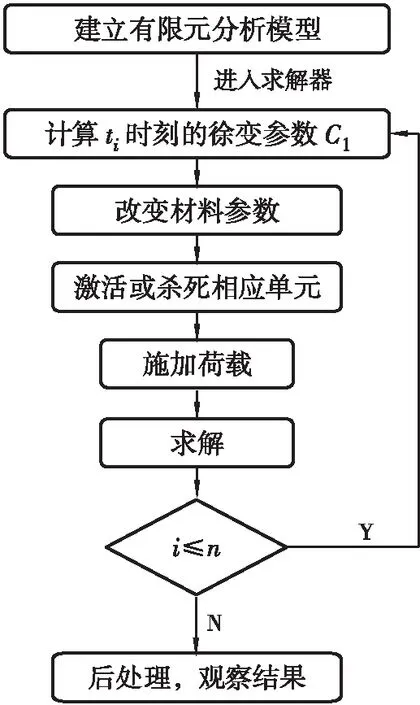
图3 徐变计算流程图
4 有限元模拟
使用ANSYS APDL建立该桥参数化有限元模型(见图4),其中,主拱圈部分及交界墩使用Solid65三维实体单元模拟,扣、锚索采用杆单元Link10模拟,扣塔构件采用梁单元Beam188模拟;两拱脚及交界墩底采用固结约束方式,锚索在锚锭处模拟为固结,扣塔立柱与横向联系间设置虚拟刚性梁。扣索扣点与主拱圈实体单元共节点。利用ANSYS生死单元技术模拟主拱圈实际施工阶段。进行各施工阶段计算分析前,提前在前处理器中生成所有单元。进行施工阶段分析时,先用EKILL命令“杀死”所有单元。某施工阶段达到强度或安装完成的单元用ELIVE命令激活;扣锚索索力的施加采用降温法模拟,扣锚索的拆除通过“杀死”单元模拟;用集中力和集中弯矩模拟拱圈节段混凝土湿重及挂篮模板重的施加,因主拱圈截面为实体单元,不便施加集中力和集中弯矩,在每个节段浇筑分界面处设置质量节点MASS21作为加载节点,然后将节段浇筑分界面连同质量节点继续截面刚化,并将集中力和集中弯矩施加于加载节点,拱圈自重通过ACEL命令施加于各施工阶段。

图4 ANSYS有限元模型图
在进行徐变计算分析时,取时间间隔Δt=10,假定年平均环境湿度70%。以拱圈合龙为计算终止工况,考虑整个悬臂浇筑过程中徐变效应与索力耦合作用下拱圈线形及应力影响。
5 计算结果分析
根据施工图纸,分节段激活拱圈各节段,施加索力及其他外荷载,进入PRESS模块进行结构静力分析,在每个时间步长内将材料徐变参数重新赋值更新,进行正装迭代求解,依次类推,直至全桥合龙。
使用MATLAB编制徐变计算程序,对整个施工过程中徐变系数进行计算,提取前90 d C60混凝土徐变系数计算结果,具体如表1所示。
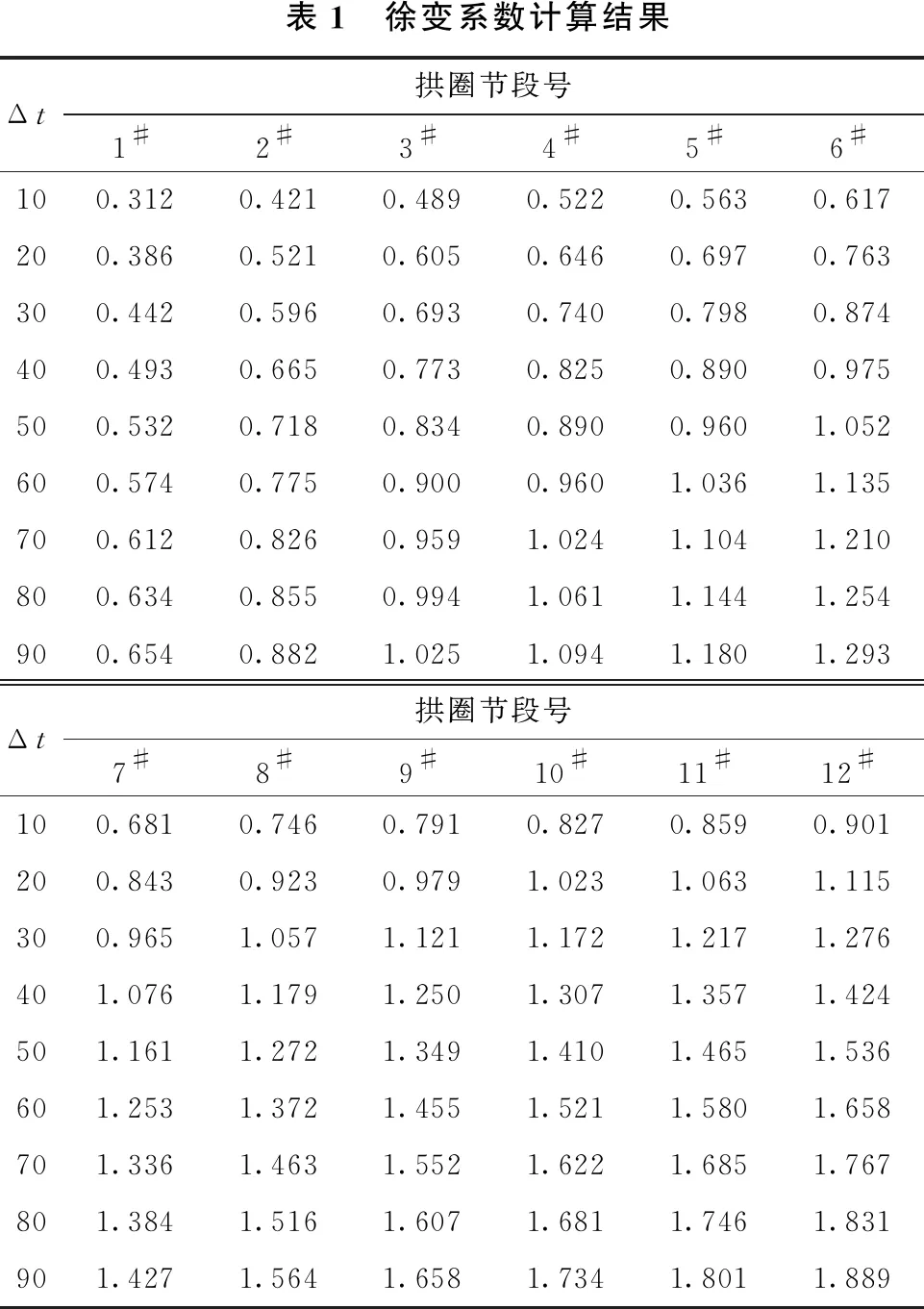
表1 徐变系数计算结果Δt拱圈节段号1#2#3#4#5#6#100.3120.4210.4890.5220.5630.617200.3860.5210.6050.6460.6970.763300.4420.5960.6930.7400.7980.874400.4930.6650.7730.8250.8900.975500.5320.7180.8340.8900.9601.052600.5740.7750.9000.9601.0361.135700.6120.8260.9591.0241.1041.210800.6340.8550.9941.0611.1441.254900.6540.8821.0251.0941.1801.293Δt拱圈节段号7#8#9#10#11#12#100.6810.7460.7910.8270.8590.901200.8430.9230.9791.0231.0631.115300.9651.0571.1211.1721.2171.276401.0761.1791.2501.3071.3571.424501.1611.2721.3491.4101.4651.536601.2531.3721.4551.5211.5801.658701.3361.4631.5521.6221.6851.767801.3841.5161.6071.6811.7461.831901.4271.5641.6581.7341.8011.889
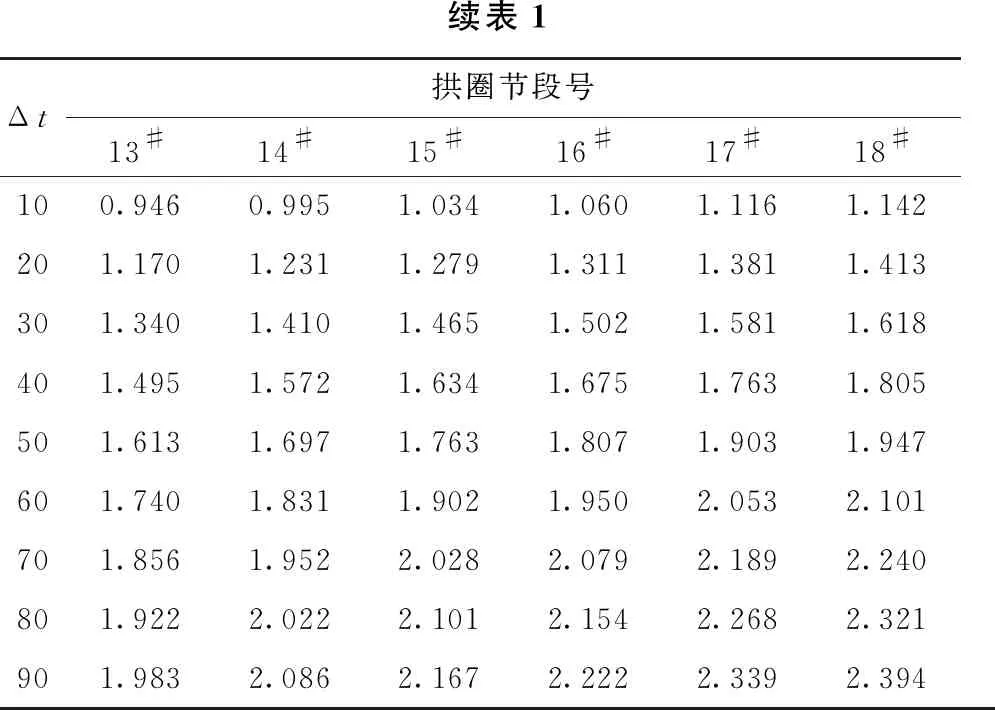
续表1Δt拱圈节段号13#14#15#16#17#18#100.9460.9951.0341.0601.1161.142201.1701.2311.2791.3111.3811.413301.3401.4101.4651.5021.5811.618401.4951.5721.6341.6751.7631.805501.6131.6971.7631.8071.9031.947601.7401.8311.9021.9502.0532.101701.8561.9522.0282.0792.1892.240801.9222.0222.1012.1542.2682.321901.9832.0862.1672.2222.3392.394
根据计算求解的徐变系数,将其分别导入ANSYS对应的施工阶段命令流中,调用ANSYS一阶优化模块,对扣索初拉力进行分阶段修正(见表2)。
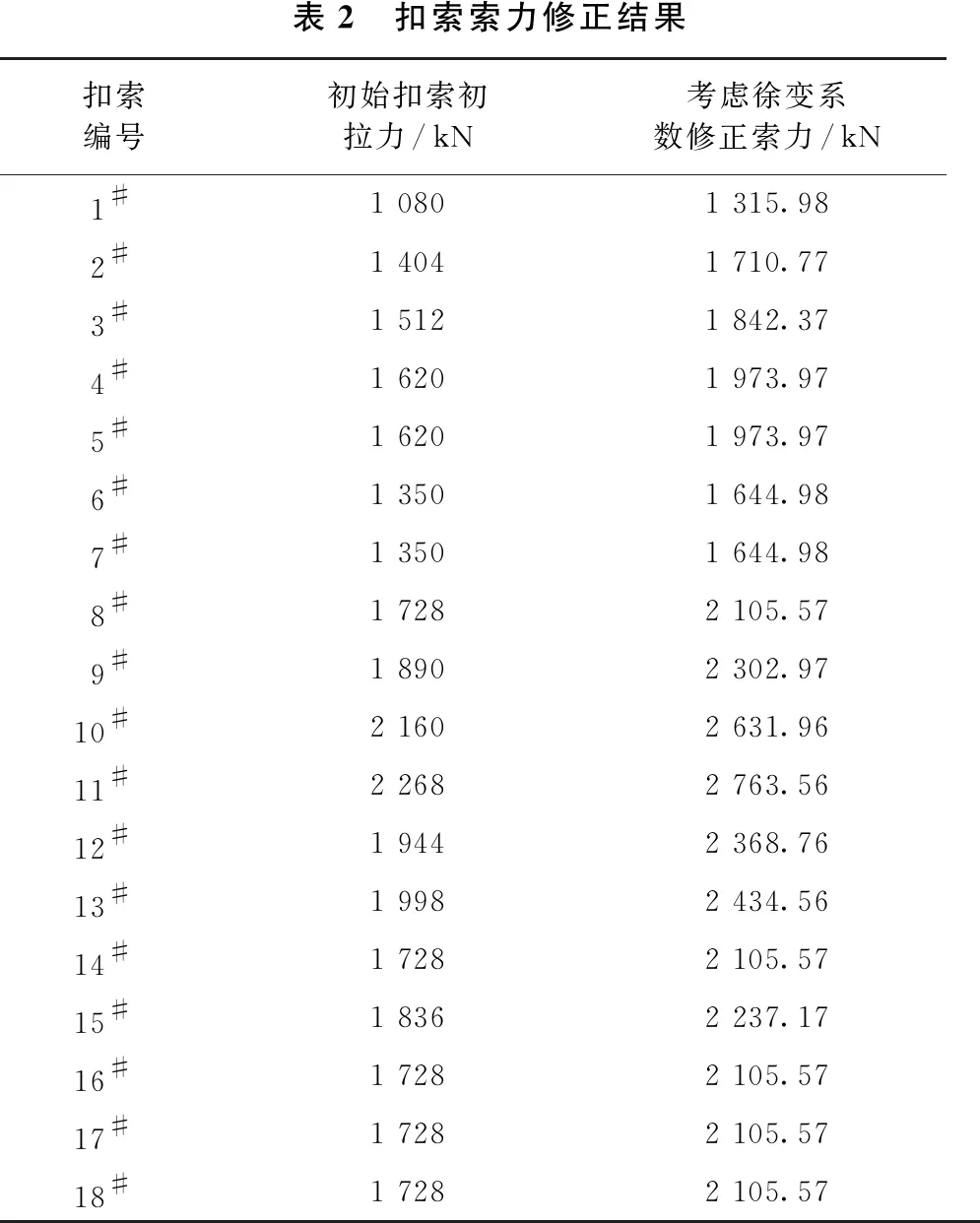
表2 扣索索力修正结果扣索编号初始扣索初拉力/kN考虑徐变系数修正索力/kN1#1 0801 315.982#1 4041 710.773#1 5121 842.374#1 6201 973.975#1 6201 973.976#1 3501 644.987#1 3501 644.988#1 7282 105.579#1 8902 302.9710#2 1602 631.9611#2 2682 763.5612#1 9442 368.7613#1 9982 434.5614#1 7282 105.5715#1 8362 237.1716#1 7282 105.5717#1 7282 105.5718#1 7282 105.57
5.1 拱圈节段变形结果分析
选取合龙工况下拱圈整体变形结果进行分析,计算分析计入拱圈节段自重、扣锚索拉力、横隔板、挂篮、徐变效应等引起的拱圈节段竖向变形值,计算结果如表3所示。
计算结果表明:
1) 计入收缩徐变后,由于节段混凝土端头下挠,导致拱圈竖向变形值降低,最大差值为19.1mm,,发生在拱圈第18#节段浇筑完成后。

表3 徐变效应对拱圈截面竖向变形影响结果对比拱圈节段号不考虑徐变效应节段最大竖向变形/mm考虑徐变效应节段最大竖向变形/mm18.37.2210.29.6311.59.8413.810.5514.611.2616.213.6718.114.5819.815.7921.616.51023.417.11126.318.61229.119.41331.519.81433.618.61534.219.21635.918.41736.818.81837.619.1 注:节段竖向变形向上为“+”,向下为“-”。
2) 随着悬臂浇筑节段的进行,徐变效应对拱圈变形的影响越来越明显,在实际施工时应予以重视,以防因为徐变效应导致预拱度不足拱圈合龙困难。
5.2 拱圈节段受力结果分析
提取合龙工况下拱圈节段各截面最大拉应力结果,对比分析不考虑徐变效应及徐变效应与扣索力耦合2种情况下对拱圈截面应力影响规律,具体如表4、图5所示。
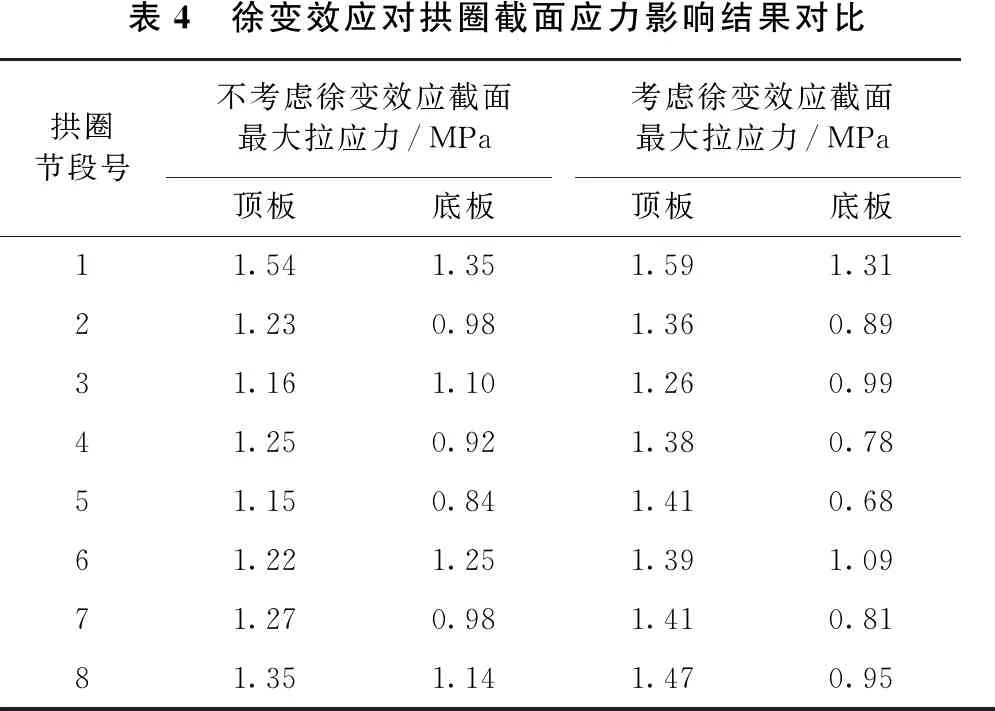
表4 徐变效应对拱圈截面应力影响结果对比拱圈节段号不考虑徐变效应截面最大拉应力/MPa考虑徐变效应截面最大拉应力/MPa顶板底板顶板底板11.541.351.591.3121.230.981.360.8931.161.101.260.9941.250.921.380.7851.150.841.410.6861.221.251.391.0971.270.981.410.8181.351.141.470.95
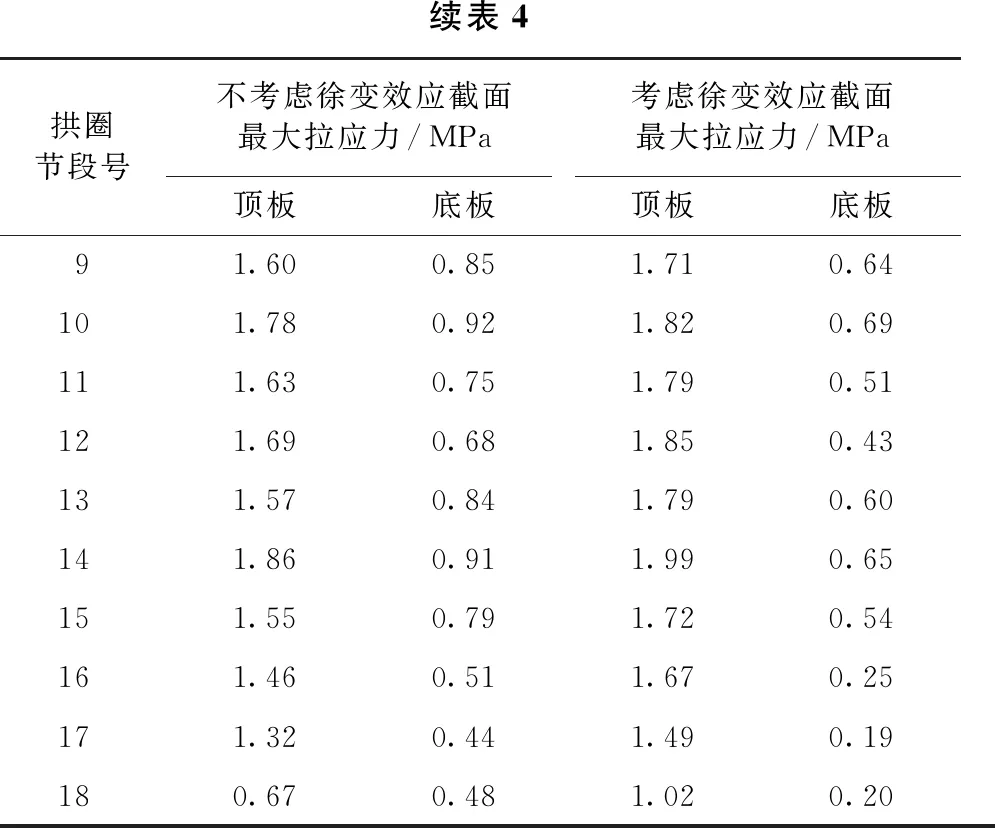
续表4 拱圈节段号不考虑徐变效应截面最大拉应力/MPa考虑徐变效应截面最大拉应力/MPa顶板底板顶板底板91.600.851.710.64101.780.921.820.69111.630.751.790.51121.690.681.850.43131.570.841.790.60 141.860.911.990.65151.550.791.720.54161.460.511.670.25171.320.441.490.19180.670.481.020.20

图5 施工阶段拱圈节段截面最大拉应力对比(MPa)
计算结果表明: ① 考虑徐变效应后,由于拱圈节段混凝土下挠,导致截面顶板拉应力增大,最大增量工况为拱圈第18#节段浇筑后,为0.35MPa;底板拉应力减小,最大下降0.28MPa,位于第18#节段浇筑后; ② 根据对比结果,顶、底板拉应力差值随着拱圈悬臂浇筑的进行越来越大,分析原因是因为混凝土龄期差,导致了徐变系数不同,从而产生的徐变应力有一定差别。
6 结论
以某在建悬臂浇筑拱桥为研究对象,基于线性徐变理论,分析了拱圈悬臂浇筑过程中徐变效应对拱圈节段变形及截面应力的影响规律,得到以下结论:
1) 徐变效应导致拱圈节段在悬臂浇筑过程中下挠,且随着浇筑进行,该现象越来越明显,该桥最大变形差为19.1mm,在实际施工确定立模标高时须予以考虑,以防拱圈合龙困难。
2) 徐变效应导致拱圈在悬臂浇筑过程中顶板拉应力增大,底板拉应力减小,考虑徐变效应后,该桥顶板拉应力最大为1.99MPa,已逼近C60混凝土抗拉强度设计值2.04MPa,须通过调整扣索索力对截面应力进行调控,避免拱圈在施工过程中开裂。
3) 随着施工阶段的进行,徐变效应对拱圈截面应力的影响越来越明显,在实际施工过程中应予以重视。

