常数变易法在微分、差分方程中的应用
任国静
( 山东财经大学数学与数量经济学院,250014,济南 )
1 引 言
常数变易法是常微分方程研究中所特有的一种求解方法.目前,常微分方程教材中,通常只介绍线性微分方程的常数变易法,包括一阶线性方程、高阶线性方程,以及一阶线性方程组[1-3].因此,常数变易法被看作是连接线性非齐次微分方程与相应的齐次方程的桥梁.近年来,已有多位学者探讨了常数变易法在微分方程求解中的应用[4-6]. 除了进行定量的计算,常数变易法在研究微分方程定性理论中也有重要应用,例如,在证明关于形式自伴微分算子的最大亏指数定理时用到了常数变易法[7].通过深入的分析,我们揭示了常数变易法的本质思想,并将这种方法应用于非线性微分方程的求解.另外,差分方程可以看成是微分方程的离散化,因而也可以用常数变易法求解[8,9].不论是高阶线性差分方程,还是一阶向量差分方程,只要知道对应齐次方程的通解,即可用常数变易法求出非齐次方程的通解.
2 常数变易法的本质思想

y′=p(x)y+q(x),
(1)
注意到y=y(x)是x的函数,方程右边可以写成y(p(x)+q(x)y-1(x)).形式上分离变量、两边积分得

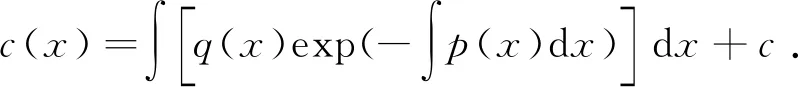
再代入形式解可得方程(1)的通解为
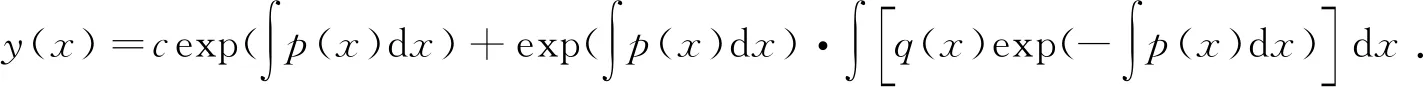

3 常数变易法在微分方程和差分方程中的推广
抓住常数变易法的思想本质,可以将其应用于非线性微分方程和差分方程的求解中.下面将分别给出几类微分方程和差分方程的求解方法和求解公式.
3.1一阶非线性微分方程考虑如下形式的一阶非线性微分方程
y′=p(x)q(y)+H(x,y).
(2)
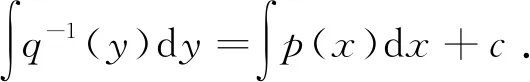
c′(x)=q-1(y)H(x,y).
(3)
方程(3)是以c(x)为未知函数的一阶微分方程. 理论上,只要能由(3)求出c=c(x),便可得到方程(2)的通解.特别地,如果H(x,y)可以写成以下形式
(4)
则由方程(4)可得c′(x)=h1(x)h2(c),这是关于c(x)的变量可分离方程. 如果H(x,y)可以写成以下形式
(5)
则由方程(3)可得c′(x)=h1(x)c(x)+h2(x)cn(x),这是关于c(x)的一阶线性方程(n=0,1)或者伯努利方程(n≠0,1),求出c(x)便可得到方程(2)的通解.下面对于方程(4)和(5),给出q(y)和H(x,y)的几类具体形式和通解公式.
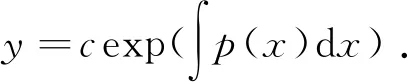

(6)

情况1H(x,y)=q(x)yn,n≠0,1.
从而得到伯努利方程为

情况3H(x,y)=h(y/x),且p(x)=1/x.
此时方程(2)为通常所说的齐次方程.对这种方程,在一般教材中是做替换u=y/x,把它化为变量分离方程.这里用常数变易法求解.首先求出方程y′=y/x的通解为y=cx,再令y=c(x)x代入原方程得c′(x)x=h[c(x)].分离变量,两边积分求出c(x),便可得到原方程的通解.

(7)
如果H(x,y)与y无关,则方程(7)是关于c(x)的一阶线性非齐次方程.
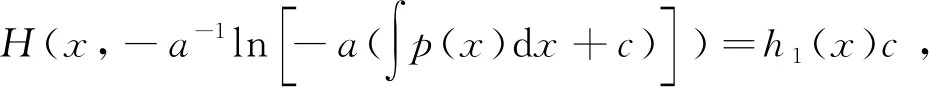
对于上述两种情况,利用3.1.1的方法或者直接利用公式求出c(x),便可得到原方程的通解.


代入(3)式得

(8)
如果H(x,y)=h1(x)h-1(y),则方程(8)是关于c(x)的一阶线性非齐次方程.同样,利用3.1.1的方法求出c(x),便可得到原方程的通解.
3.2线性差分方程本节将常数变易法的思想应用到差分方程的求解中.如果已知线性齐次差分方程的通解, 则利用常数变易法可求出原线性非齐次方程的通解. 以下分别对n阶线性差分方程和一阶向量差分方程给出求解方法和通解公式.
3.2.1n阶线性差分方程n阶线性差分方程的一般形式为
x(t+n)+a1(t)x(t+n-1)+…+an(t)x(t)=f(t),t∈Z+,
(9)
其中f(t),ai(t),i=1,2,…,n,是已知离散变量的函数,an(t)≠0.假设x1(t),x2(t),…,xn(t)是方程(9)对应的齐次方程x(t+n)+a1(t)x(t+n-1)+…+an(t)x(t)=0的一个基础解组(即n个线性无关解),则该齐次方程的通解为x(n)=c1x1(t)+c2x2(t)+…+cnxn(t).下面用常数变易法求方程(9)的通解.令
x(t)=c1(t)x1(t)+c2(t)x2(t)+…+cn(t)xn(t)
(10)
是方程(9)的解,由(10)式得
x(t+1)=c1(t)x1(t+1)+c2(t)x2(t+1)+…+cn(t)xn(t+1)
+Δc1(t)x1(t+1)+Δc2(t)x2(t+1)+…+Δcn(t)xn(t+1),
(11)
这里Δc(t)=c(t+1)-c(t).令Δc1(t)x1(t+1)+Δc2(t)x2(t+1)+…+Δcn(t)xn(t+1)=0并代入(11)式得
x(t+1)=c1(t)x1(t+1)+c2(t)x2(t+1)+…+cn(t)xn(t+1).
重复上面的过程n-1次,可以得到
x(t+k)=c1(t)x1(t+k)+c2(t)x2(t+k)+…+cn(t)xn(t+k),k=1,2,…,n-1,
(12)
且
Δc1(t)x1(t+k)+Δc2(t)x2(t+k)+…+Δcn(t)xn(t+k)=0,k=1,2,…,n-1.
(13)
将(10)式和(12)式代入方程(9)得
Δc1(t)x1(t+n)+Δc2(t)x2(t+n)+…+Δcn(t)xn(t+n)=f(t).
(14)
注意到(13)式和(14)式是关于Δci(t)的线性方程组,即
记

(15)
这里ci为任意常数,Wi(t)是用(0,…0,1)T替换W(t)中的第i列所得的行列式.再将(15)式代入(10)式便可得到方程(9)的通解公式为
(16)
特别地, 当n=2时, 公式(16)可以写成
(17)
由此可以看出, 与线性微分方程类似,线性差分方程初值问题的解是存在唯一的,且其通解等于它的一个特解加上其对应的齐次方程的通解.
3.2.2 一阶向量差分方程 一阶向量差分方程的一般形式为
X(t+1)=A(t)X(t)+B(t),t∈Z+,
(18)

进一步可求得
从而方程(18)的通解为
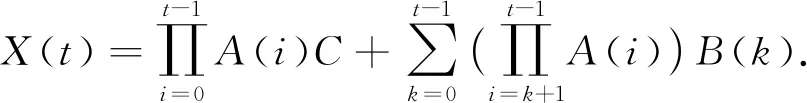
3.3 算 例
例1求方程y′=-12x-3ey-x(e-y+6x-2)的通解.
解这是一阶非线性微分方程.先解方程y′=-12x-3ey,它的通解是e-y=-6x-2+c.令原方程的解为e-y=-6x-2+c(x),代入原方程化简得c′(x)=6x-1·c(x)-x·c2(x).这是关于c(x)的伯努利方程,可以求得c(x)=(cx-6+x2/8)-1.原方程的通解为e-y=-6x-2+(cx-6+x2/8)-1,其中c为任意常数.
例2求差分方程x(t+2)-7x(t+1)+6x(t)=t的通解.
解原方程对应的齐次差分方程x(t+2)-7x(t+1)+6x(t)=0是常系数方程,利用特征方程可以求出该方程的两个线性无关解分别为x1(t)=1,x2(t)=6t. 令x(t)=c1(t)+6tc2(t),代入原方程,或直接由方程(15)得c1(t)=-t(t-1)/10+c1,c2(t)=-t/25·6-t+c2.进而可求得方程的通解为
4 结 语
由上面的讨论和算例可以看到,常数变易法在微分方程和差分方程求解中显示出了巨大的威力.常数变易法实际上是一种变量替换,通过这种变量替换,可以将不容易直接利用初等积分法求解的复杂方程,转化成已知的、可求解的方程类型,进而求出原方程的通解.

