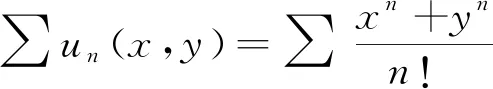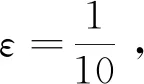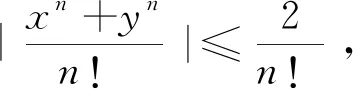函数列一致收敛性及其应用

李 萌 范进军

( 山东师范大学数学与统计学院，250358，济南 )

1 引 言

函数列的一致收敛是数学分析教材中的重要概念，对研究其极限函数的连续性、可导性和可积性具有重要的作用[1-3].目前一元函数列一致收敛的理论体系比较完善，已有一些学者对一元函数列或函数项级数的收敛性做了直观刻画[4-6].由此推广可以得到多元函数列一致收敛的理论知识[7-9]，但是二元函数列一致收敛的过程对初学者来说不够形象具体且难以理解.因此可以构造适当的二元函数列和二元函数项级数，运用MATLAB软件画出其函数图像，通过直观分析图像规律加深对函数列一致收敛动态过程的理解，为进一步探寻其极限函数的各种性质做好准备.另外函数列的一致收敛性可以推广到函数项级数的一致收敛性，因而借助MATLAB软件的直观刻画，也可以探寻判断函数项级数敛散性的新方法.

2 二元函数列一致收敛和MATLAB编程应用

2.1预备知识本文对一元函数列的相关概念进行推广得到二元函数列一致收敛的定义及相关判断方法，借助MATLAB软件将具体函数进行数据可视化，帮助初学者增加对函数列收敛过程的认识.为方便起见，给出下面的几个引理.

引理1[1]设二元函数列{fn(x,y)}与二元函数f(x,y)定义在同一区域D∈R2上，若对任意的正数ε，总存在某一正整数N,使得当n>N时，对一切的点(x,y)∈D都有

|fn(x,y)-f(x,y)|<ε，

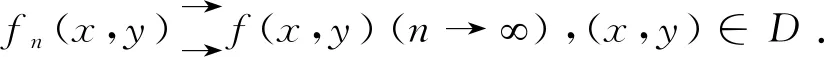
引理2[1]函数列{fn(x,y)}在区域D∈R2上一致收敛于f(x,y)的充要条件为

引理3[1]二元函数列{fn(x,y)}一致收敛于f(x,y)的几何意义：对任意的正数ε，存在某一正整数N，对于一切序号大于N的三维曲面y=fn(x,y)都落在以曲面y=f(x,y)+ε与y=f(x,y)-ε为上下边界所夹击形成的区域中.

2.2 MATLAB编程及应用

2.2.1 用MATLAB判断函数列一致收敛的方法

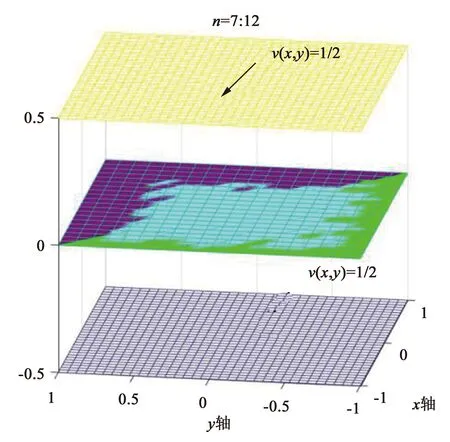
1) 方法1：依据函数列一致收敛的定义(引理1)及其几何意义(引理3)判断一致收敛性.根据函数列一致收敛的定义及几何意义可知,对于某个事先给定的ε(0<ε<1),如果存在正整数N，使得n>N时，总有曲面gn(x,y)=fn(x,y)-f(x,y)落在曲面v(x,y)=ε与曲面v(x,y)=-ε之中，则说明函数列{fn(x,y)}在区域D∈R2上一致收敛，否则就不一致收敛.因此可以借助MATLAB画出n=1∶24(或1∶m，m为充分大的正整数)的函数图像，观察曲面gn(x,y)=fn(x,y)-f(x,y)是否落在曲面v(x,y)=ε与曲面v(x,y)=-ε之中，如果都被此区域包围说明该函数列一致收敛，否则该函数列就不一致收敛.

2) 方法2:依据函数列一致收敛的充要条件(引理2)判断一致收敛性.根据函数列一致收敛的充要条件,可以用MATLAB求出对每个正整数n，gn(x,y)=fn(x,y)-f(x,y)在区域D上所取得的绝对值的最大值gmax，然后画出n与gmax的函数图像.如果当n趋于时gmax趋于0，就能说明该函数列{fn(x,y)}在区域D∈R2上一致收敛，否则就不一致收敛.

2.2.2 用MATLAB判断函数列一致收敛的具体实例

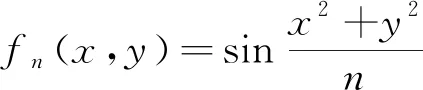
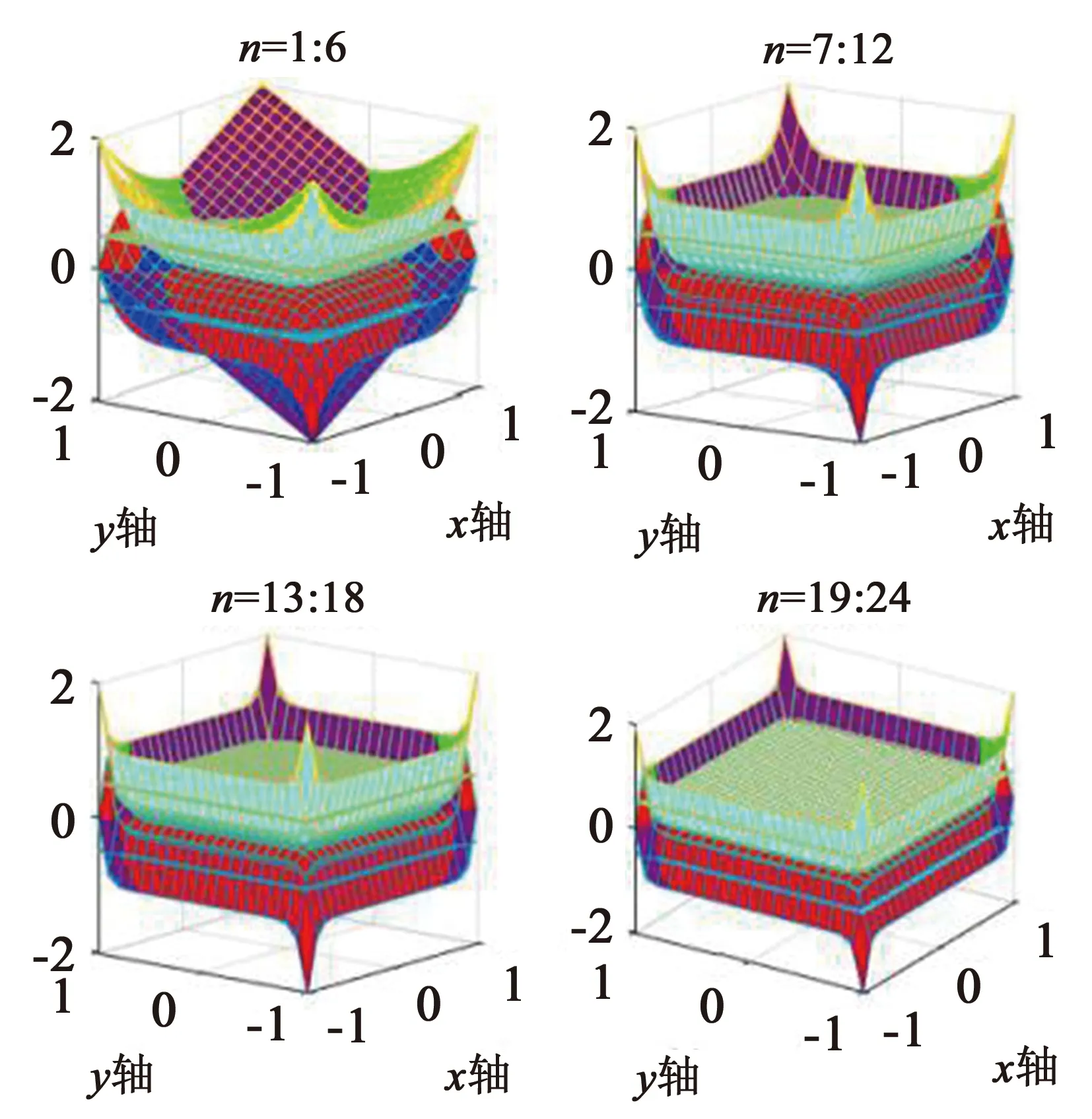
证1)(直观说明)分别用2.2.1中的方法1和方法2，借助MATLAB编程(实验结果如图1至图6所示)，将具体函数进行数据可视化，说明其在特定区域上是一致收敛的.

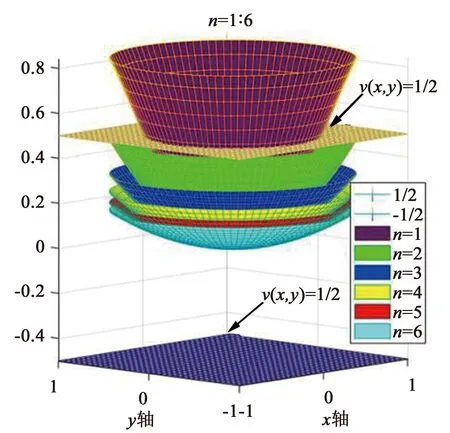
图1 n=1∶6所对应的gn(x,y)函数整体图像

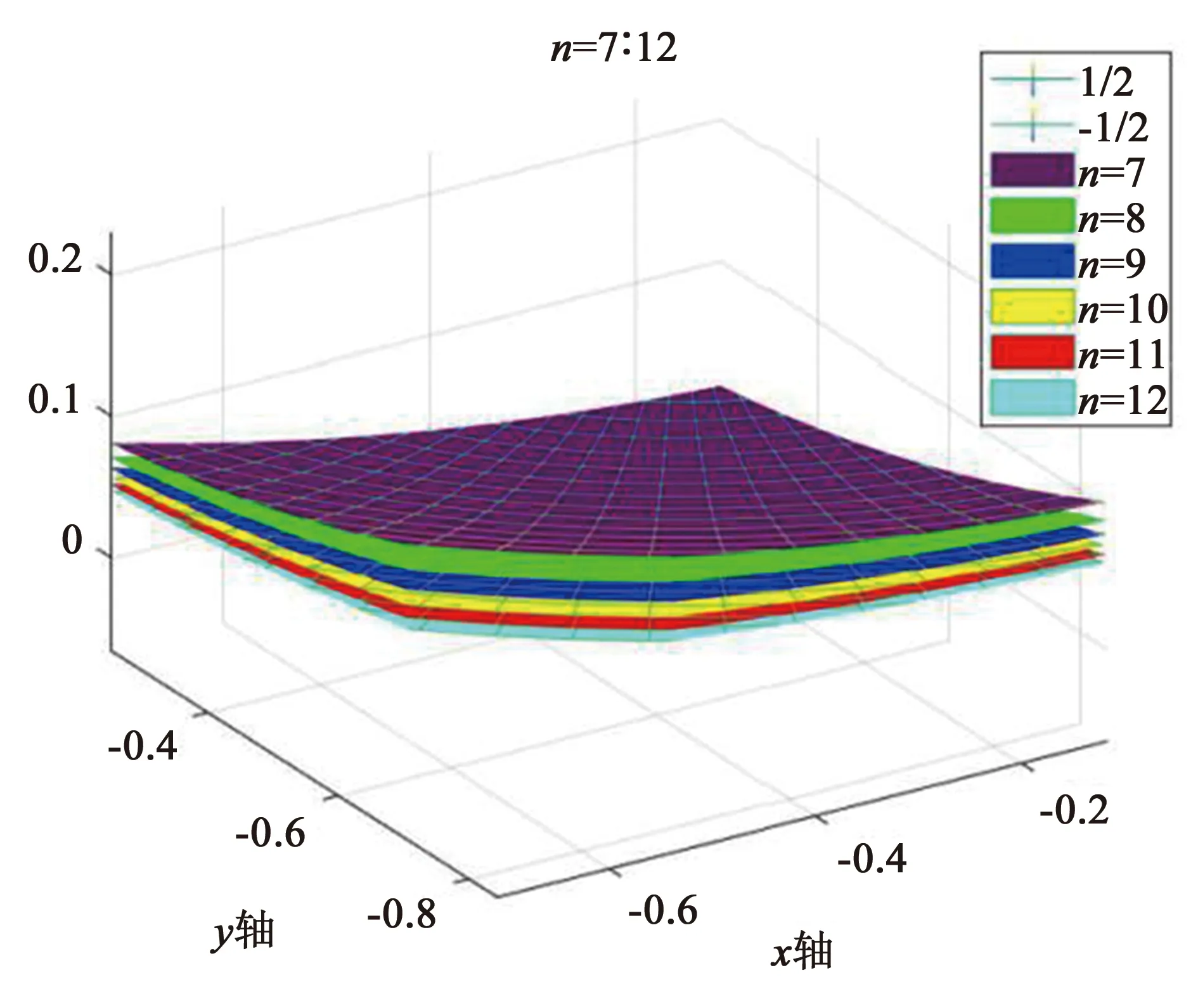
图2 n=7∶12所对应的gn(x,y)函数局部图像

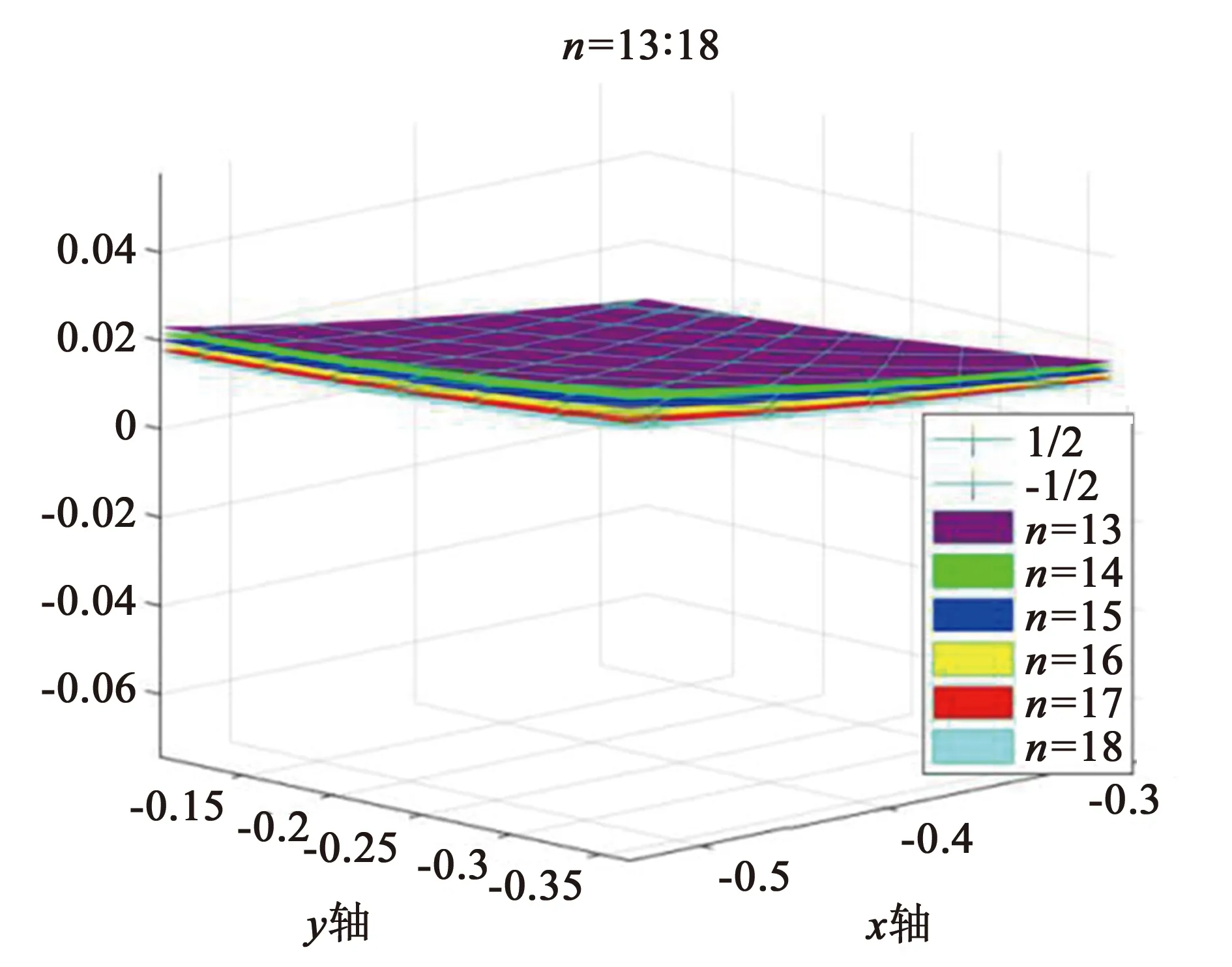
图3 n=13∶18所对应的gn(x,y)函数局部图像

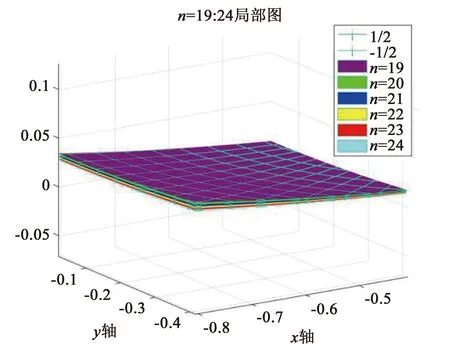
图4 n=19∶24所对应的gn(x,y)函数局部图像

图5 n=19∶24所对应的gn(x,y)函数整体图像

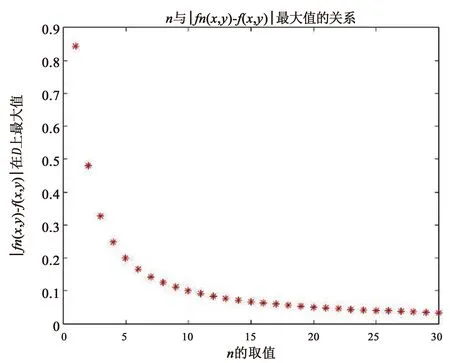
图6 n与的函数关系图像

首先，运用2.2.1中的方法1(引理3)进行编程，实验结果如下所示.

MATLAB程序：

co=[0.5,0,0.5;0,1,0;0,0,1;1,1,0;1,0,0;0.5,1,1]; %构造颜色矩阵

[thetar]=meshgrid(linspace(0,2*pi,100),linspace(0,1,20));

[x,y]=pol2cart(theta,r);

fori=1∶4

figure(i)

fmesh(@(x,y)1/2,[-1,1,-1,1])

hold on

fmesh(@(x,y)-1/2,[-1,1,-1,1])

hold on

forn=1+6*(i-1)∶6*i

z=sin((x.^2+y.^2)./n);

t=mesh(x,y,z)

set(t,′FaceColor′,...

co(n-6*(i-1),:))

hold on

end

xlabel(′x轴′) ylabel(′y轴′)

switchi

case 1

title(′n=1∶6′);

case 2

title(′n=7∶12′);

case 3

title(′n=13∶18′);

case 4

title(′n=19∶24′);

end

hold on

end

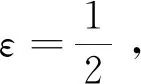
然后，运用2.2.1中的方法2(引理2)进行编程，实验结果如下所示.

MATLAB程序：

[thetar]=meshgrid(linspace(0,2*pi,100),linspace(0,1,20));

[x,y]=pol2cart(theta,r);

forn=1∶30

z=sin((x.^2+y.^2)./n);

M(n)=max(max(z));

end

plot(M,′*r′)xlabel(′n的取值′)

title(′n与|fn(x,y)-f(x,y)|最大值的关系′)

ylabel(′|fn(x,y)-f(x,y)|在D上最大值′)

解1)(直观说明)首先，用2.2.1中的方法1(引理3)进行编程，实验结果如下所示(图7).

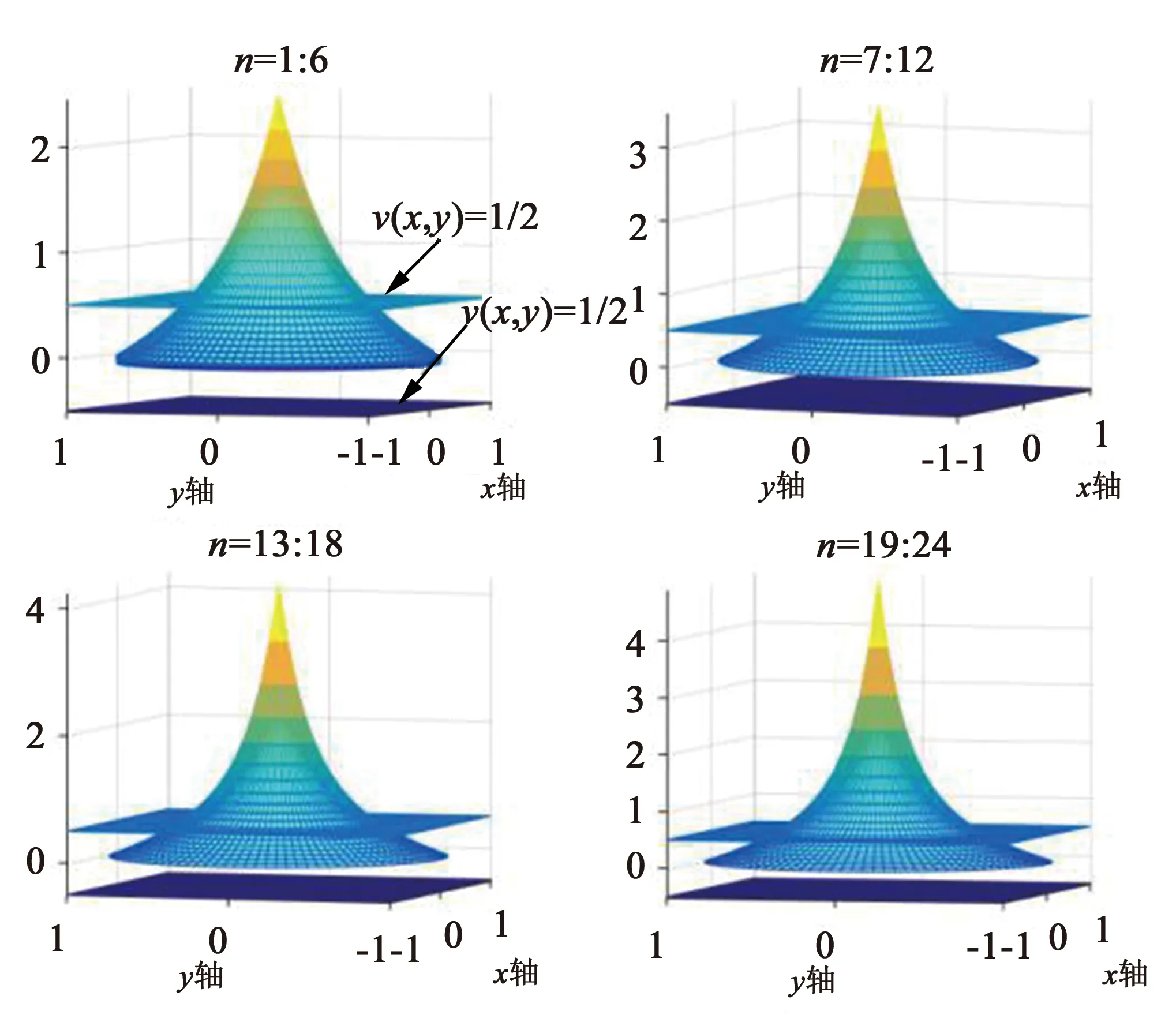
图7 n=1∶24所对应的gn(x,y)函数整体图像

然后，运用2.2.1中的方法2(引理2)进行编程，实验结果如下所示(图8).

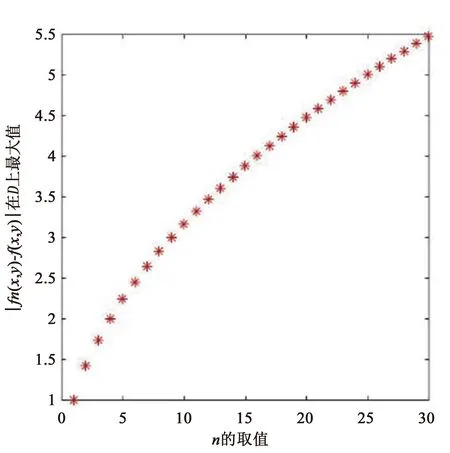
图8 n与的函数关系图像

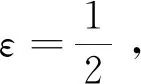
3 二元函数项级数一致收敛和MATLAB编程应用

3.1 预备知识

引理4[1]设{Sn(x,y)}是函数项级数∑un(x,y)的部分和函数列，若{Sn(x,y)}在区域D中一致收敛于二元函数S(x,y),则称∑un(x,y)在D中一致收敛于S(x,y).

引理5[1]函数项级数∑un(x,y)在区域D中一致收敛于二元函数S(x,y)的充要条件为

引理6[2]函数项级数∑un(x,y)在区域D中一致收敛的必要条件是函数列{un(x,y)}在D中一致收敛于0.

引理7[1]设二元函数项级数∑un(x,y)定义在点集D∈R2上，∑Mn为收敛的正项级数，若对任意(x,y)∈D有|un(x,y)|≤Mn(n=1,2,3……)，则二元函数项级数∑un(x,y)在点集D∈R2上一致收敛.

3.2 MATLAB编程及应用

3.2.1 用MATLAB判断函数项级数一致收敛的方法 运用MATLAB判断函数项级数一致收敛的方法步骤如下.

步骤1：由引理6可知，先验证函数列{un(x,y)}是否一致收敛于0，如果不一致收敛于0，则函数项级数∑un(x,y)在区域D中不一致收敛，如果一致收敛于0，则进行下一步；

步骤2：用MATLAB求出函数项级数∑un(x,y)的部分和函数列{Sn(x,y)} 及其和函数S(x,y)；

步骤3：用2.2.1中的两种方法之一验证{Sn(x,y)}在区域D中是否一致收敛.

3.2.2 用MATLAB判断函数项级数一致收敛的具体实例

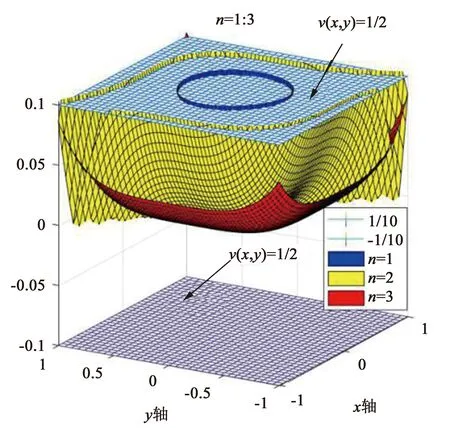
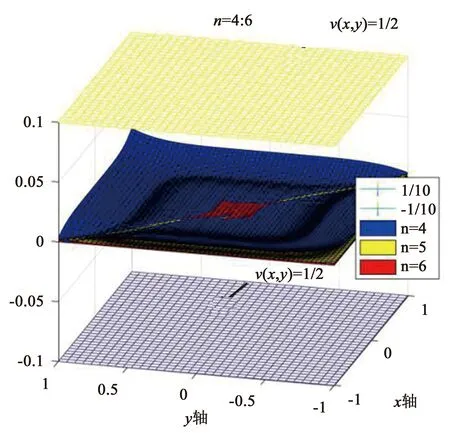
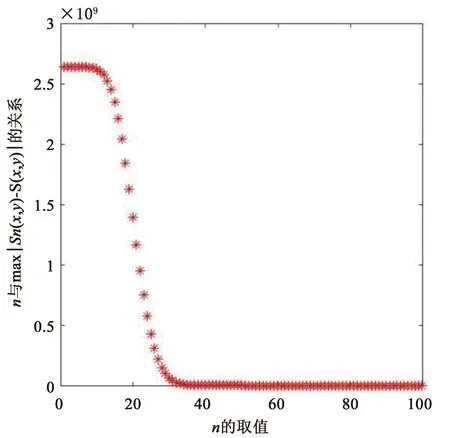
例3已知函数项级数为∑un(x,y)=∑(xn+yn),判断该函数项级数在区域D={(x,y)|-1

证1)运用MATLAB编程进行实验验证.当取定(x,y)∈D时，un(x,y)=xn+yn→0 (n→),因此{un(x,y)}的极限函数是u(x,y)=0.借助MATLAB软件,利用2.2.1中的方法1，画出函数gn(x,y)=un(x,y)-u(x,y)=x2+yn在区域D中当n=1∶24时所对应的函数图像(图9).

图9 n=1∶24所对应的un(x,y)-u(x,y)函数图像

2) (严格证明)由于函数列{un(x,y)}在区域D中的极限函数是u(x,y)=0，并且

由引理2知{un(x,y)}在区域D中不一致收敛，与MATLAB实验运行结果一致.

证1)运用MATLAB编程进行实验验证.

图10 n=1∶6所对应的un(x,y)-u(x,y)函数整体图像

图11 n=7∶12所对应的un(x,y)-u(x,y)函数图像

步骤2：用MATLAB求出函数项级数∑un(x,y)的部分和函数列{Sn(x,y)} 及和函数S(x,y).

首先，用MATLAB求出函数项级数∑un(x,y)的部分和函数列{Sn(x,y)}，程序代码如下所示.

symsxykn

un=(x^k+y^k)/sym(′factorial(k)′);

sn=symsum(un,k,0,n);

然后，用MATLAB求出函数列{Sn(x,y)}的极限函数S(x,y),程序代码如下所示.

symsxyn;

symsum((x^n+y^n)/sym(′factorial(n)′),n,0,inf)

ans =exp(x) + exp(y)

由此可见函数列{Sn(x,y)}的极限函数是S(x,y)=ex+ey.

步骤3：判断函数列{Sn(x,y)}是否一致收敛.下面分别运用2.2.1中的方法1和方法2进行实验验证.

co=[0.5,0,0.5;0,1,0;0,0,1;1,1,0;1,0,0;0.5,1,1];%构造颜色矩阵

symsxykn;

s=symsum((x^n+y^n)/sym(′factorial(n)′),n,0,inf);

fori=1∶2

figure(i)

fmesh(@(x,y)1/10,[-1,1,-1,1])

hold on

fmesh(@(x,y)-1/10,[-1,1,-1,1])

hold on

for m=1+3*(i-1)∶3*i

un=(x^k+y^k)/sym(′factorial(k)′);

sn=symsum(un,k,0,m);

t=ezsurf(abs(sn-s),...

[-1,1,-1,1]);

set(t,′FaceColor′, ...co(m-3*(i-1)+2,∶))

hold on

end

xlabel(′x轴′)

ylabel(′y轴′)

switch i

case 1

title(′n=1∶3′);

case 2

title(′n=4∶6′);

end

图12 n=1∶3所对应的Sn(x,y)-S(x,y)函数图像

图13 n=4∶6所对应的Sn(x,y)-S(x,y)函数图像

[X,Y]=meshgrid(-1∶0.1∶1,-1∶0.1∶1);

symsxynk;

s=symsum((x^n+y^n)/sym(...

′factorial(n)′),n,0,inf);

form=1∶100

un=(x^k+y^k)/sym(′factorial(k)′);

sn=symsum(un,k,0,m);

z=abs(sn-s);

g=matlabFunction(z);

fori=1∶length(X)

forj=1∶length(Y)

zz=g(i,j);

end

sm(m)=max(max(zz));

end

plot(sm,′*r′);xlabel(′n的取值′)

ylabel(′n与max|Sn(x,y)-S(x,y)|的关系′)

图14 n与的函数关系图像

由图14分析可得随n趋向过程中趋于0，因此根据引理5可得函数项级数在区域D中是一致收敛的.