置换上的一类Hopf代数结构

赵明泽 李慧兰

( 山东师范大学数学与统计学院，250358，济南 )

1 引 言

对称群中的置换已经被应用于多个研究领域，如计算机科学、财务分析和交通模拟等.由于Hopf代数结构的稳定性往往揭示了组合数学中深层次的性质和联系，所以Hopf代数逐渐成为代数组合学的重要研究内容之一.自1979年Joni等人[1]在研究置换的离散结构时发现这些离散结构具有天然的Hopf代数结构， 到2003年Aguiar等人[2]提出了组合Hopf代数的概念，越来越多的组合Hopf代数被发现和研究，并且很多Hopf代数与代数表示理论、代数几何、图论等研究领域有紧密的联系[3，4].

由文献[5]可知，Hopf代数结构是由代数结构和余代数结构、双代数结构逐步推导得来的.Hopf代数拥有双代数结构，且代数结构与余代数结构兼容，并满足对极映射条件.在代数B中，若存在一个直和分解B=⊕i≥0Bi，其中Bi中的元素为i阶的，且任意p阶与q阶元素的积是p+q阶元素，则B是分级代数.类似地，可以给出分级余代数的定义.如果一个环R上的分级双代数H=⊕i≥0Hi满足H0≅R，则称H为分级连通的.由于任何分级连通的双代数都拥有唯一的对极映射，所以分级连通的双代数都是Hopf代数.

在组合数学中，置换一词传统上是指一组有序的排列.1983年，基于 “字母”之上，Lothaire[6]将“字母”按照一定的顺序排列并将这些有序列构成了一个集合，之后Lothaire在这个集合上加上二元运算，进一步引入了代数结构.设A是一个字母表，A中的每个元素都是一个字母，由这些字母组成的“单词”是一个有限序列，所有的单词所构成的集合记为A*.Lothaire、Eilenberg和Garsia等人[6-8]在集合A*上引入洗牌积运算，并证明了这种运算满足交换律和结合律.2012年，Enjalbert等人[9]在这个置换集合上提出了拟积运算，其中定义的洗牌拟积与切牌余积是兼容的.

设一个n阶置换是由n个元素所构成的一个排列.将所有[n]:={1,2,…,n}上的置换所组成的集合称为n阶对称群，记为Sn.定义集合S∶=∪n≥0Sn，并赋予了S0={ε}，其中ε是空置换.2002年，通过研究非交换元素上对称函数的Hopf代数结构，Aguiar等人[10,11]分析了置换上的Malvenuto-Reutenauer Hopf代数结构，并给出了在这个Hopf代数结构上所存在的对极映射，但其中定义出的洗牌积运算计数方式不满足交换律.2018年，Bergeron等人[12]提出了“全局下降点”的概念.并以此为基础，在置换集合S上重新定义了洗牌积运算的计数方式，使其满足了交换性且(kS，ш)是一个代数结构.进一步，Bergeron等人又提出在这个代数结构中洗牌积ш和切牌余积Δ是兼容的，即(kS，ш，Δ)是一个双代数.本文证明了置换集合(kS，ш，Δ)具有双代数结构.通过对极映射的定义，找出了(kS，ш，Δ)上的对极映射公式并给出了证明.

2 Hopf代数

首先回顾一下关于Hopf代数的相关知识，详细的结果可参看文献[5].

设交换环R上的模B存在R线性映射η和μ:

η:B⊗RB→B(乘)，

μ:R→B，

且映射满足图1所示的交换图表，则η是乘积映射，μ是单位映射，模B是一个R代数，记为(B，η，μ).为了记号简洁，将η(g，f)记为gf.

图1 η和μ交换图表

设交换环R上的模B存在R线性映射Δ和ν:

Δ:B→B⊗RB(余乘)，

ν:B→R，

且映射满足图2所示的交换图表，则Δ是余乘映射，ν是余单位映射，模B是一个R余代数，记为(B，Δ，ν).

图2 Δ和ν交换图表

若(B，η，μ，Δ，ν)既是R代数又是R余代数，且B满足下列互相等价的兼容条件之一：

1)η和μ满足余代数同态，

2)Δ和v满足代数同态，

则B是一个双代数.

设B是一个双代数，若B存在一个R线性映射S:B→B，使得对任意的b∈B满足

(1)

图3 对极映射

拥有对极映射的双代数是Hopf代数.

3 置换上的Hopf代数

设kS∶=⊕n≥0kSn是一个分级的向量空间，其中kSn是数域k上由Sn张成的向量空间.

设ω是在Sn中的一个置换，其阶数为n.在这个置换上，第一个数字前面的位置记为位置0、第i个数字和第i+1个数字之间的位置记为位置i、最后一个数字后面的位置记为位置n，这些位置被称为置换ω上的“间隙”[12].

对于n阶置换ω上的间隙γ，若满足运算ω([γ])=[n][n-γ]，则称此处的间隙为“全局下降点”，其中0和n一直都是全局下降点.没有其他全局下降点的置换称为原子置换.因此，每一个置换ω都拥有一个唯一的分解式ω=ω1·ω2·…·ωl，其中ω1，…，ωl都是原子置换.S中每一个置换的长度都是以其含有的原子置换的个数来定义的，即置换ω的长度为|ω|=l.

例1设置换ω=7564231∈S7,求它的全局下降点及分解式.

解全局下降点有: 0，1，3，4，6，7，分解式为ω=7·56·4·23·1.

每一个置换ω都存在唯一的标准式，记为st(ω).例如st(756)=312.所以，之后记例1中ω分解式的标准式为1·12·1·12·1，重新计数时，从右到左计数.

设置换α∈Sm和β∈Sn，定义置换α·β∈Sm+n为

例2已知α=132∈S3，β=2413∈S4，计算α·β.

解α·β=132·2413=5762413.

显然α·β在间隙m处是一个全局下降点.相反地，给定一个置换ω∈Sm+n，且在间隙m处是一个全局下降点，则存在唯一的一组置换α∈Sm和β∈Sn使得ω=α·β.

定义1设置换ω∈S，且其唯一的标准分解式为ω=ω1·ω2·…·ωl，其中ω1，...，ωl都是原子置换，则切牌余积为

(2)

例3求置换7564231在进行切牌余积运算后的结果.

解Δ(7564231)=⊗1·12·1·12·1+1⊗(12·1·12·1)+(1·12)⊗(1·12·1)

+(1·12·1)⊗(12·1)+(1·12·1·12)⊗1+1·12·1·12·1⊗

定义2在S上定义洗牌积ш，对于任意的π、ω∈S，定义πшε:=π，εшω:=ω,

(μ·ν)ш(σ·τ):=μ·(νшω)+σ·(πшτ)，

(3)

其中π=μ·β，ω=σ·τ，μ和σ是非平凡的原子置换.

置换中的洗牌积ш作用在置换的标准分解式上，它是一个标准的交换积.

例4已知π=312=1·12∈S3，ω=4213=1·213∈S4，长度都是2，求πшω的结果.

解πшω=312·4213

=1·12·1·213+1·1·12·213+1·1·213·12

+1·1·12·213+1·1·213·12+1·213·1·12

=7564213+7645213+7643512+7645213+7643512+7546312.

对于任意的p阶置换集合Sp和q阶置换集合Sq，通过定义1和定义2可得ш(kSp⊗kSq)=kSp+q，μ(k)=kS0.所以，代数(kS，ш，μ)是分级的.同时，(kS，Δ，ν)是分级余代数.

4 主要结果

定理1(kS，ш，Δ)是一个Hopf代数.

因为分级连通的双代数都是Hopf代数.已有kS0≅k，所以只需要证明(kS，ш，Δ)是双代数，即洗牌积ш与切牌余积Δ是兼容的.

引理1洗牌积ш与切牌余积Δ是兼容的，即

Δ(πшω)=Δ(π)шΔ(ω)，

(4)

其中π=π1·…·πi·…·πs，ω=ω1·…·ωj·…·ωt.

在证明这个引理之前，可以计算并观察下面的例题.

例5已知π=312=1·12，ω=231=12·1∈S3，长度都是2，求Δ(312ш231)的结果.

解

Δ(312ш231)

=Δ(1·12·12·1+1·12·12·1+1·12·1·12+12·1·12·1+12·1·1·12+12·1·1·12)

从上面对Δ(312ш231)的计算过程可以发现，其中的每个结果项都将被符号″⊗″分为左边和右边.所以，从每个项的特点出发，可以根据在″⊗″之前的312和231中原子置换的数目来计算.

因此，在计算Δ(πшω)时，可以得到其每一个结果项也都是被符号″⊗″分为左右两边的.所以，置换π=π1·…·πi·…·πs和ω=ω1·…·ωj·…·ωt在经过洗牌积运算后，可以根据其每一个结果项中在符号″⊗″前面的原子置换数目来填写Δ(πшω)的结果.也就是说，在符号″⊗″前面的那些原子置换是由″i″和″j″的值决定的.

接下来证明引理1.这里不妨假设m≤n.

证当Δ(πшω)的所有结果项中″⊗″的左边有″π″中原子置换的个数为i=0，1，2，...，s，且有″ω″中原子置换的个数为j=l时，记符合要求的结果项之和为Δ(πшω)|j=l，其中0≤l≤t.

当i=0，1，2，…，s，j=0时,这个条件要求结果项中″⊗″的左边不存在任何ω中的原子置换″ωj″.那么符合要求的结果项之和为

+(π1·π2ш·)⊗(π3·…·πsшω)+…+(π1·…·πsш)⊗(шω)

:=Δ(πшω)|j=0.

当i=0，1，2，…，s，j=k(0≤k≤t)时，符合要求的结果项之和为

(шω1·…·ωk)⊗(πшωk+1·…·ωt)

+(π1шω1·…·ωk)⊗(π2·…·πsшωk+1·…·ωt)

+···+(π1·…·πsшω1·…·ωk)⊗(·шωk+1·…·ωt)

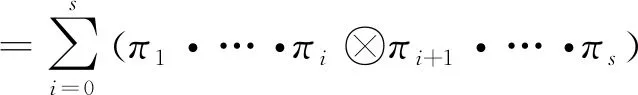
:=Δ(πшω)|j=k

所以，Δ(πшω)的所有结果项中″⊗″的左边有″π″中原子置换的个数为i=0，1，2，...，s，有″ω″中原子置换的个数为j=k(0≤k≤t)，结果项之和的通项公式为

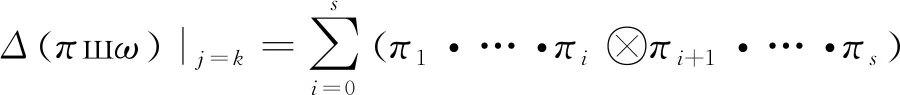
Δ(πшω)的所有结果项中″⊗″的左边有″π″中原子置换的个数为i=0，1，2，...，s，且有″ω″中原子置换的个数为j=0，1，2，...，t，这也就是说将j=0，1，2，...，t时的t+1个结果项之和的通项公式相加可得

Δ(πшω)

=Δ(πшω)|j=0+Δ(πшω)|j=1+Δ(πшω)|j=2+…+Δ(πшω)|j=k+…+Δ(πшω)|j=t

通过观察可以发现上面ш左边括号里的式子都是一样的，提取公因式可得

Δ(πшω)

+(ω1·ω2⊗ω3·…·ωt)+…+(ω1·…·ωk⊗ωk+1·…·ωt)+…+(ω1·…·ωt⊗)]

=Δ(π1·…·πs)шΔ(ω1·…·ωt)

=Δ(π)шΔ(ω).

因此，可以得出在置换中洗牌积ш与切牌余积Δ是兼容的.所以，(kS，ш，Δ)是一个双代数.

引理1证明了(kS，ш，Δ)是一个双代数; 又因为它是分级连通的，所以(kS，ш，Δ)是一个Hopf代数，即定理1得证.

例6已知π=312=1·12，ω=231=12·1∈S3，长度都是2，证明Δ(πшω)=Δ(π)шΔ(ω).

证Δ(π)шΔ(ω)=Δ(1·12)шΔ(12·1)

=(⊗1·12+1⊗12+1·12⊗)ш(⊗12·1+12⊗1+12·1⊗)

=(⊗1·12)ш(⊗12·1)+(⊗1·12)ш(12⊗1)+(⊗1·12)ш(12·1⊗)

+(1⊗12)ш(⊗12·1)+(1⊗12)ш(12⊗1)+(1⊗12)ш(12·1⊗)

+(1·12⊗)ш(⊗12·1)+(1·12⊗)ш(12⊗1)+(1·12⊗)ш(12·1⊗).

再根据例5可以得出证明.

(kS，ш，Δ)是一个Hopf代数，那么它就存在一个对极映射，下面的引理2给出了它的对极映射公式及相关证明.

引理2(kS，ш，Δ)拥有唯一的对极映射S，对于任意长度为l的置换π=π1·π2·…·πl有

S(π)=(-1)lπl·πl-1·…·π2·π1.

(5)

证易知对于Hopf代数(kS，ш，Δ)中的任意元素都满足公式(1).

由于公式(1)中左右等号两边是对称的，所以这里只需证明公式的右边.

首先，根据公式(1)对置换π进行切牌余积运算

其次，根据公式(1) 对置换π进行(S⊗1)∘Δ(π)运算,可得

最后，对(S⊗1)∘Δ(π)进行洗牌积ш运算，可得

ш∘(S⊗1)∘Δ(π)

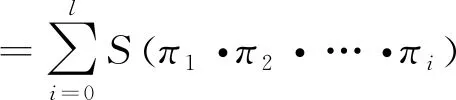
=шπ1·π2·…·πl+(-1)1(π1)ш(π2·…·πl)

+(-1)2(π2·π1)ш(π3·…·πl)+…+(-1)n(πl·πn-1·…·π2·π1)ш

=π1·π2·…·πl-π1·π2·…·πl-π2·(π1шπ3·…·πl)

+π2·(π1шπ3·…·πl)+π3·(π2·π1шπ4·…·πl)

-π3·(π2·π1шπ4·…·πl)-π4·(π3·π2·π1шπ5·…·πl)

+…+(-1)l-1πl-1·(πl-2·…·π1шπl)+(-1)l-1πl·(πl-1·…·π2·π1ш)

+(-1)lπl·πl-1·…·π2·π1ш

=0.

这就证明了ш∘(S⊗1)∘Δ(π)=0，从而对极映射S对于公式(1)等号右边是成立的.同理，可以证明等号左边也是成立的，即ш∘(1⊗S)∘Δ(π)=0，引理2得证.