涡旋阵列光场与涡旋光镊技术

高垣梅 尚春雷 卢城臻 蔡阳健

( 山东师范大学物理与电子科学学院，250358，济南 )

随着光场调控技术的发展，新型光场及其调控技术越来越受到关注.涡旋光束(Vortex Beam)具有螺旋形波前和轨道角动量，并以螺旋的方式进行传播，其具有相位因子exp(ilφ)，其中φ为方位角，l为拓扑荷数，l可以取任意值，l的正负决定涡旋光束波前的螺旋方向，每个光子都携带lћ的轨道角动量(Orbital Angular Momentum)[1].轨道角动量在光束与粒子相互作用时表现出传递性，因而可以设法实现操控粒子，螺旋形波前构造使得涡旋光束呈暗中空，轴上光场强度为零，中心的相位具有不确定性被称为相位奇点.涡旋相位环绕中心相位奇点一周相位变化2l.图1 展示了不同拓扑荷数l的涡旋光束的波前结构、相位分布和光强分布，可见拓扑荷数l与这些特征密切相关.

图1 几种涡旋光束 (a)波前结构；(b)相位分布；(c)光强分布

柱坐标系中，涡旋光束的传播方程一般为

E(r,φ,z)=E0exp(-ikz)exp(ilφ).

(1)

涡旋光束具有螺旋波前结构、中心相位奇点并携带轨道角动量，在许多领域既是研究的热点，也是研究的工具.例如在光通讯领域[13-15]，相比传统光束增加了拓扑荷数l这一维度，轨道角动量可以编码信息，使其在光通信方面具有容量大、保密性强等优势.在光学微操纵领域[16,17]，可利用轨道角动量的传递性设法驱动粒子沿轨道旋转，改变涡旋光束拓扑荷数l的大小和正负，粒子所受驱动力的大小和方向也随之改变.此外，在超分辨成像[18,19]、量子信息存储[20，21]等领域涡旋光束也有着广泛的应用.

涡旋阵列光束由按照某种排列方式分布的多个光学涡旋构成，相比于单支涡旋光束，涡旋阵列光束增加了空间分布这一自由度，因而在光通信应用中可以提高信息编码容量，在光学微操纵领域可以同时捕获、操纵多个微粒，是有力的研究工具[22].涡旋阵列光束的产生方法亦有多种，如空间光调制-全息法[23-25]、干涉法(分振幅干涉法[26-28]、分波面干涉法[29,30]).通过达曼光栅[31-33]也可以产生涡旋阵列光束.

利用光来操控粒子由来已久，1987 年 Ashkin等人[34]在实验中发现了光学镊子效应.若透明微粒的折射率大于周围介质，并受到强激光的聚焦，光子便可将动量传递给微粒，通过力学效应形成的光阱，从而实现对微粒的操控[35-38]，这就是光镊的实质.光镊捕获微粒主要利用了光束与微粒相互作用时梯度力和散射力[39]，其过程可简单描述为：激光聚焦后形成微米级光斑，光强梯度非常高，梯度力将高折射率的微粒推到光强最大处.由于微粒对光的反射、折射和吸收，还会产生一个沿着光传播方向的散射力，当梯度力大于散射力时便实现对微粒的捕获.被作用微粒的线度为几到几百微米，根据微粒线度与波长的关系，可将光与微粒的作用归纳为三种模型：微粒的线度远大于入射光波长时为几何光学模型[40]，微粒的线度远小于入射光波长时为瑞利散射模型[41]，微粒的线度与入射光波长相当时为电磁散射模型[42].可以看到光镊技术具有无接触、无损伤的特点，使得光镊技术广泛地应用于现代科学研究的各个领域，在原子物理中用来研究原子冷却[43]、玻色-爱因斯坦凝聚[44]，在生物和医学领域，用来操控细胞融合和生物大分子[45,46].涡旋光束的引入，为光镊技术带来了新的力学效应.涡旋光束携带轨道角动量并能够传递给微粒，不仅可以捕获微粒，还可以使微粒旋转， 轨道角动量使粒子绕光束轴转动，自旋角动量使其自转，实现对粒子的三维捕获[47,48].非涡旋的光镊通常捕获比周围介质折射率相对高的粒子，而暗中空结构的涡旋光束可用来捕获低折射率微粒[49-51].涡旋阵列光场与单涡旋光束相比,优势明显，应用前景广阔.本文研究了利用单涡旋光束按不同排列方式组合，生成不同结构的二维涡旋阵列光场；利用二维阵列光场与圆心处沿z轴平面波相干涉，产生三维阵列空心光束、三维阵列涡旋光束.随后进行了利用涡旋光束在光镊中捕获粒子并驱动粒子旋转的实验，实现了涡旋光束粒子微操纵.

1 涡旋光束合成二维涡旋阵列

本节主要讨论二维涡旋阵列光场的产生，通过数值模拟考察多涡旋光束干涉产生圆环形晶格和多涡旋光束的合成，并通过实验产生晶格光场和涡旋阵列光束.

1.1环形晶格径向指数为零(p=0)的单环拉盖尔高斯光束表达式为

(2)

束腰半径w0相同，拓扑荷数l不同的 LG 涡旋光束同轴叠加，表达式为

LG=LGl1+LGl2+LGl3+….

(3)

光强为I=LG×LG*，相位φ为φ=arg[LG] .

1.1.1 双光束叠加合成单环形晶格 两组LG涡旋光束同轴叠加产生单环暗晶格光场，第一组叠加光束的拓扑荷数正负号相同，绝对值不同，第二组叠加光束的拓扑荷数正负号相反，绝对值相同.数值模拟结果如图2所示.

图2 双光束叠加合成单环形晶格的光强和相位 (a)和(c)l1=2,l2=10；(b)和(d)l1=6,l2=-6

图2 (a) 为一暗环晶格的光强图，由拓扑荷数l分别为2和10的两LG涡旋光束叠加而成，可以看到，光束中心的光强为零，8个暗斑均匀分布于环上.图2 (b) 为一亮环晶格的光强图，由拓扑荷数l分别为6和-6的两LG涡旋光束叠加而成，可以看到，光束中心的光强为零，12个亮斑均匀分布构成亮环.图2(c)为暗环晶格的相位图，中心红色圆圈内为l=2的相位奇点，周围8个绿色圆圈内为l=1的相位奇点，相位奇点处光强为零.图2(d)为亮环晶格的相位图，相位值为0或2π，无相位奇点.通过分析光强和相位，l1和l2正负号相同时，涡旋光束共轴叠加形成环暗晶格，且暗斑数量为|l1-l2|；l1和l2互为相反数时，叠加形成环亮晶格，且亮斑数量为|l1-l2|.

1.1.2 多光束叠加合成双光环晶格 多束涡旋光共轴叠加情况：三束光，l的正负号相同且绝对值不同，产生双暗环晶格光场；四束光，l两正两负且每组绝对值相同，产生双亮环晶格光场.

图3 双光环晶格的光强和相位分布 (a)和(c)l1=2,l2=10,l3=18；(b)和(d) l1=2,l2=-2,l3=18,l4=-18

仿照上小节的讨论，将多光束叠加产生双光环晶格模拟结果呈现在表1中.

表1 多光束叠加产生双光环晶格

不难发现，晶格的光强和相位与多光束的拓扑荷数有密切的关系：当l1、l2、l3正负号相同时，内层环暗斑数量为|l1-l2|而外层环的暗光斑数量为|l2-l3|；当多光束满足l1=-l2，l3=l4时，其内环和外环的亮花瓣状光斑数量分别为|l1-l2|和|l3-l4|，与双光束合成单环晶格的结论相似.

1.1.3 环形晶格实验结果 如图4所示，波长532 nm的激光经凸透镜L1和L2扩束，通过偏振片成为良好的线偏振光，再经BS分成两束光，一束照射于SLM，将相位全息图加载到SLM，另一束经4f系统滤波，由CCD捕捉，可得晶格光场.图5、图6分别展示了上述四种配置下所得晶格的光强分布图，图幅右下角附有模拟光强图，实验得到的晶格光场与数值模拟的结果基本一致.

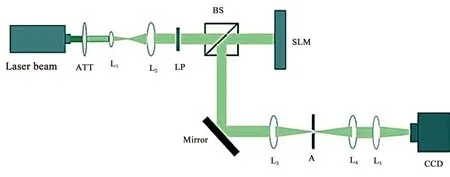
图4 环形光晶格实验装置 ATT:衰减片；LP:偏振片；BS:分束棱镜； SLM:空间光调制器；Mirror:反射镜；A:光阑；CCD:电荷耦合器；L1-L5:凸透镜

图5 单环晶格光强实验图 (a) l1=2,l2=10，(b) l1=6,l2=-6

图6 双环晶格光强实验图(a) l1=2,l2=10,l3=18；(b) l1=2,l2=-2,l3=18,l4=-18

1.2二维涡旋阵列光场多束涡旋光按一定排列方式可构成阵列涡旋光场，在排列组合过程中，形成了空间排布这一新的自由度，阵列涡旋光束可分为线性排布结构、矩阵排列结构、径向排列结构.

1.2.1 线性排列的涡旋阵列 涡旋阵列光场线性排列有N束涡旋光束，相邻的涡旋光束之间的距离为xd或yd,阵列中第n个涡旋光束的光场表达式为

或

(4)

其中，当n为偶数，n∈(-N/2,N/2)，当n为奇数，n∈(-(N-1)/2,(N-1)/2)， (x,y)为直角坐标系.横向或纵向线性排列的涡旋阵列光束的光场表达式为

或

(5)

图7是5束线性排列的的涡旋光束，其拓扑荷数l=6，束腰半径x0=0.5 mm，间距xd=5 mm，图(a)为横向排列的光强数值模拟图，(c)为对应的相位分布图，直角坐标系中各涡旋光束的中心坐标分别为(-10,0)、(-5,0)、(0,0)、(5,0)、(10,0)；(b)为纵向排列的光强数值模拟图，(d)为对应的相位分布图.图7(b)和(d)纵向排列分布的光强图和相位图，各涡旋光束的中心坐标分别为(0,10)(0,5)(0,0)(0,-5)(0,-10).

图7 线性排列的涡旋阵列光场 (a)和(b)分别为横向和纵向排列的光强分布；(c)和(d)为对应的相位分布

1.2.2 矩阵排列的涡旋阵列光场 呈矩阵排列的涡旋光束阵列(简称涡旋光束矩阵)由M×N束子涡旋构成，在x、y方向相邻涡旋光束的之间的距离分别表示为xd、yd,涡旋矩阵中某一个涡旋子光束的光场表达式为

(6)

其中，当M,N为奇数，m∈(-(M-1)/2,(M-1)/2),n∈(-(N-1)/2,(N-1)/2)，当M,N为偶数，m∈(-M/2,M/2),n∈(-N/2,N/2)，矩涡旋光束矩阵的光场表达式为

(7)

我们模拟了2×2和3×3型涡旋光束矩阵，如图8所示，子光束拓扑荷数l=6，束腰半径w0=0.5 mm,间距5 mm，图(a)和(c)是2×2型涡旋光束矩阵的光强和相位模拟结果，每个子光束中心坐标分别为(-5,5)、(5,5)、(-5,-5)、(5,-5)；图(b)和(d)是2×2型涡旋光束矩阵的光强和相位模拟结果，每个子光束中心坐标分别为(-5,5)、(0,5)、(5,5)、(-5,0)、(0,0)、(5,0)、(-5,-5)、(0,-5)、(5,-5).

图8 涡旋光束矩阵 (a)和(c)2×2型光强和相位分布；(b)和(d)3×3型光强和相位分布

1.2.3 径向排列的涡旋阵列光场N束涡旋光分布于在半径为r的圆上，可构成径向排列的涡旋光束阵列，相邻子光束之间关于圆心的夹角为a0=2π/N，子光束的光场表达式为

(8)

其中，方位角an=na0,n=1,2,3，…，N，(rcosαn,rsinαn)为阵列中第n束涡旋光在极坐标系中的位置，径向排列的涡旋阵列光场表达式为

(9)

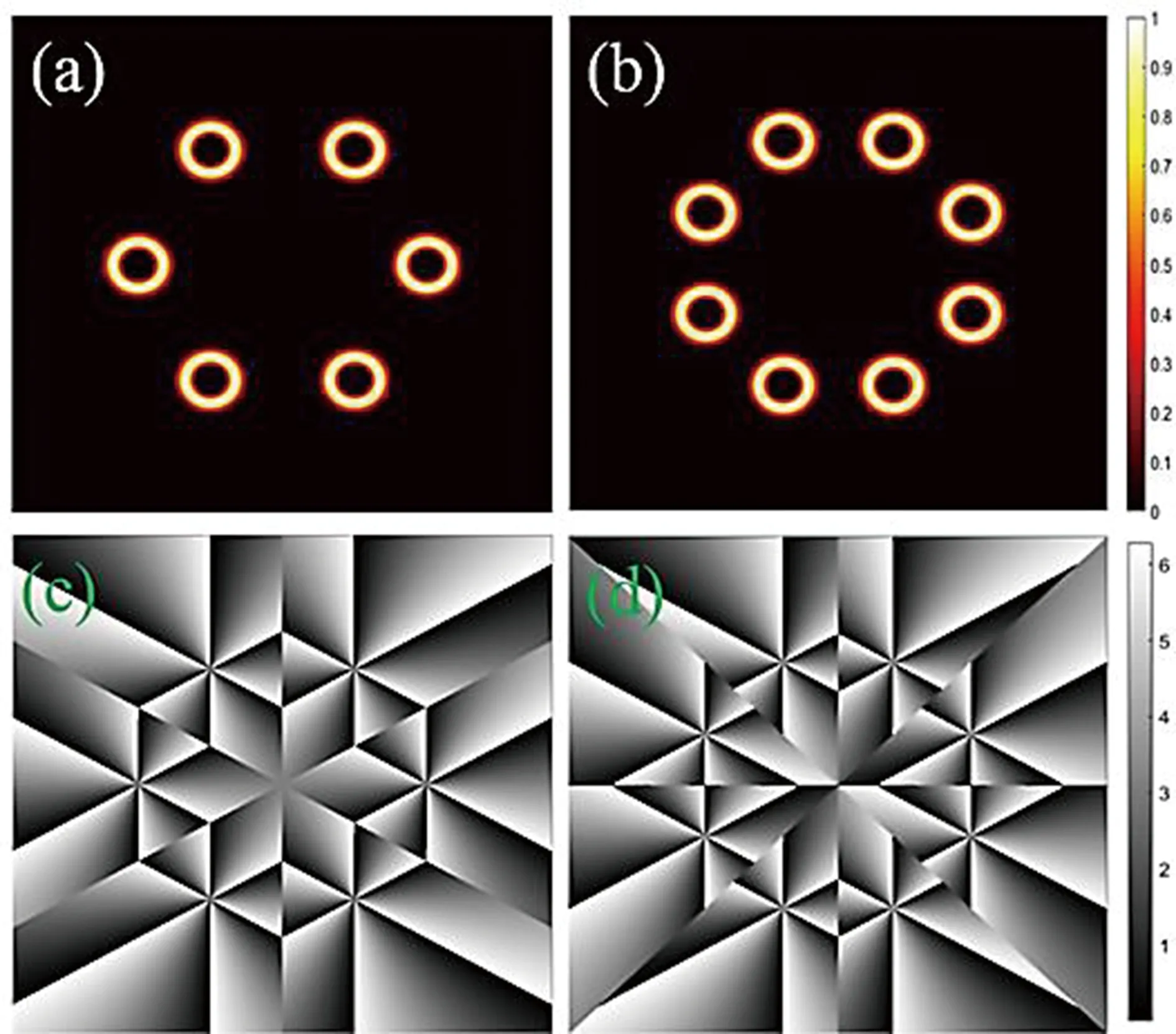
图9 径向排列的涡旋阵列光场 (a)和(c) 为6子光束径向排列的光强和相位分布；(b)和(d) 为8子光束径向排列的光强和相位分布

六束拓扑荷数l=6，束腰半径l0=0.5 mm的涡旋光束径向排列构成径向半径r=8 mm的径向涡旋阵列，图9(a)和(c) 展示了其光强和相位模拟结果，各子光束中心坐标分别为

1.2.4 涡旋阵列光场实验结果 实验光路如图4所示，将图7、8、9的相位全息图加载至空间光调制器，产生的涡旋阵列光场可由CCD实时接收并显示于计算机.实验得到的光场如图10、11、12所示，线性排列、矩阵排列和径向排列的涡旋光场均与模拟结果一致.此外，子涡旋的拓扑荷数l、束腰半径w0以及它们之间的相对位置可以自行设定，因而能够灵活地产生所需的涡旋阵列光场.

图10 线性排列的涡旋阵列实验图 (a) 5束横向排列；(b)5束纵向排列

图11 矩阵涡旋光场实验图 (a)2×2分布；(b)3×3分布

图12 径向排列的涡旋阵列实验图 (a)6束子涡旋;(b) 8束子涡旋

1.3完美涡旋阵列对于传统涡旋光束，中心亮环半径与其拓扑荷数l成正比，当l变化时，中心亮环半径与随之变大或变小，而对于完美涡旋光束，亮环半径不再依赖于拓扑荷数l，使其在光操控、光通讯等方面越来越成为研究的热点，例如，研究者可以针对不同微粒改变光束轨道角动量而不改变光束的亮环半径，提高工作效率.完美涡旋阵列光场表达式为

(10)

将式(10)分别代入式(5)、(6)、(7)，可得到线性排列、矩阵排列和径向排列的完美涡旋阵列光场，如图13所示，阵列中每个子涡旋半径相同而拓扑荷数不同.图13(a)和(d)为线性排列的涡旋光场，l=1,2,3,4,5，图13(b)和(e)为矩阵排列的涡旋光场,l=1,2,3,4，图13(c)和(f)径向排列光场，l=1,2,3,4,5,6.

2 三维密集阵列光场

上节讨论了常见的二维涡旋阵列光场的产生，接下来讨论利用二维涡旋阵列光场产生三维涡旋阵列光场.三维光子晶格光场是三维结构光场的主要存在形式，利用一束平面光在光的传播方向与二维光子晶格光束相干涉，可以产生三维光子晶格光场.若与平面光相干涉的是二维涡旋阵列光场的光束，则可以产生三维周期性涡旋阵列光场，这是一种密集型涡旋阵列光场.我们首先构造二维周期阵列光场，六束平面波对称分布同一个圆上，它们初始相位构成完整的涡旋相位，即六束平面波总初始相位移动为2lπ.六束平面波经傅里叶变换相干生成各种二维周期阵列光场，二维阵列光场与沿z轴传输的平面波相干涉，产生三维空心阵列光束、三维涡旋阵列光束.

2.1三维阵列光场六束平面波对称分布在同一圆上，相干叠加光场表达式为

(11)

(12)

其中，Ai为复振幅，φi为波失，r为位矢，φij为相互干涉的初相位.研究发现l=0 和l=6的光场相同，l=1和l=5的光场相同，l=2和l=4的光场相同，所以拓扑荷l只取0、1、2、3 四个值即可.六束平面波生成四种结构不同的二维周期光场，再与中间平面波干涉得到四种三维阵列光场，分别为六角型三维阵列光场、六边涡旋型三维阵列光场、Kagome型三维阵列光场和蜂窝型三维阵列光场，这四种光场横截面有一个共同点，每一个阵列单元光场都具有六重对称性.

2.2六角型三维阵列光场如图14 (a)所示，六束平面波的初始相位相同，以相同颜色标识.从图14(b)和(c)可以看出，干涉后生成以六边形为周期的光场，右下角的虚线六边形框内表示一个阵列单元，六边形的中央光强最大，六角位置处光强较弱，相位分布规律与光强分布相似，六边的相位相同且与中心的相位差相同.实验得到的涡旋阵列光场如图14(d)所示，与模拟结果一致.图15是六光束与中间一束平面波干涉产生的三维阵列光场立体结构模拟图，可以看出每个阵列单元由中央瓶子状空心光束和周围6个小椭球状光斑构成，其光强分布符合六角型三维阵列光场的光强分布.

图14 l=0干涉产生六角型三维阵列光场(a)干涉光束空间截面图;(b)干涉光强模拟;(c)干涉相位模拟;(d)光场分布实验结果

图15 l=0三维阵列光场模拟 (a)-(c)分别为光场立体结构图、俯视图和局部放大图

图16 l=1干涉产生六边螺旋型三维阵列光场 (a)干涉光束的空间截面图；(b) 干涉光强模拟；(c) 干涉相位模拟；(d) 光场分布实验结果

2.3六边螺旋型三维阵列光场如图16 (a)所示，六束平面波的初始相位不同，以不同颜色标识，相邻两束初始相位差为π/3，构成一个完整的涡旋相位2π.从图16(b)和(c)可以看出，干涉后产生六边形涡旋阵列光场，右下角的虚线六边形框内表示一个阵列单元，光强呈六边形暗中空分布，相位从0-2π顺时针渐变，相位图中心为相位奇点，涡旋相位也呈六边形排列.实验得到的涡旋阵列光场如图16(d)所示，与模拟结果一致.图17是螺旋型三维阵列光场立体结构模拟图，可以看出每个涡旋呈螺旋分布，排列密集.每个涡旋具有轨道角动量，可用于多粒子的三维操纵.

图17 l=1三维阵列光场模拟 (a)-(c)分别为光场立体结构图、俯视图和局部放大图

2.4Kagome型三维阵列光场如图18所示，当l=2时，初始相位分别为0、2π/3、4π/3、2π、8π/3、10π/3的六束光束干涉产生Kagome型三维阵列光场,光束总的初始相位移动为4π，第一四、二五、三六束平面波的相位分别相同，初始相位用三种颜色标识.生成的光场阵列单元为Kagome型，六枚光斑围成花瓣状，花瓣位于正六边形的六条边上，花瓣中心光强最大，如图18 (b)所示.从图18(c)的相位图看，六边形内是拓扑荷为l=2的涡旋相位，从0到4π渐变，六边形六角处为拓扑荷为l=1的涡旋相位，从0到2π渐变.中心的涡旋相位是逆时针旋转的，而六个角上涡旋相位是顺时针旋转的.图18(d)是实验得到的光场，与模拟的光强图基本一致.图19是模拟得到的Kagome型三维阵列光场结构图，光场并非连续分布，而是点状分布，花瓣状光斑有三种类型，每一种的初相位相同，在三维空间中分三层分布,在图19(c)用黑线标出.

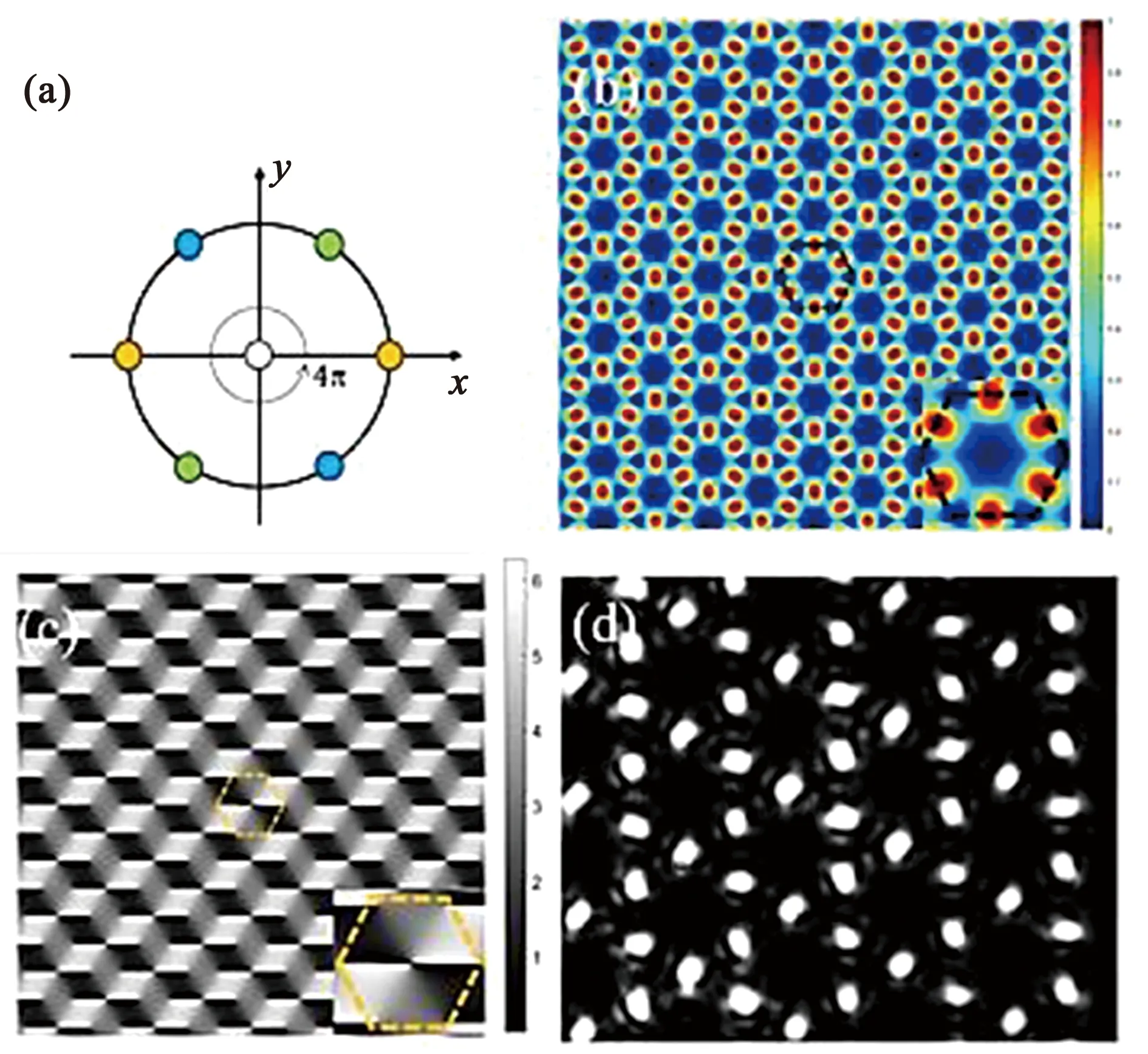
图18 l=2时干涉产生Kagome型三维阵列光场；(a)干涉光束的空间截面图；(b) 干涉光强模拟；(c) 干涉相位模拟；(d) 光场分布实验结果

图19 l=2时三维光场的模拟结果 (a)-(c)分别为光场立体结构图、俯视图和局部放大图

2.5Honeycomb型三维阵列光场如图20所示，拓扑荷数l=3、初始相位为0或π的六束光干涉产生Honeycomb型三维阵列光场,光束的总初始相位移动为6π，第一三五束初始相位相同，第二四六束初始相位相同，分别用两种颜色标识.生成阵列光场中每个阵列单元由六个圆弧三角形(别名鲁洛克斯三角形，Reuleaux Triangle)围成，呈雪花状.由图20(b)可以看到圆弧三角形呈暗中空结构.由图20(c)可以看到，阵列单元的相位呈六边形，六个为0或π的三角形相位交叉分布，相邻三角形有大小为π的相位突变.图20(d)是实验得到的Honeycomb型光场，与模拟结果一致.图21为三维光场结构图，图21(b)、(c)印证了上述分析.

图20 l=3干涉产生Honeycomb型三维阵列光场 (a)干涉光束的空间截面图；(b)干涉光强模拟；(c)干涉相位模拟；(d)光场分布实验结果

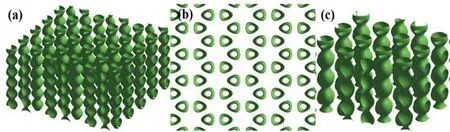
图21 l=3时三维阵列光场的模拟结果 (a)-(c)分别为整体结构图、俯视图和局部放大图

3 利用涡旋光束的粒子捕获

光具有波粒二象性，不仅具有能量还携带动量，二氧化硅是透明粒子，其折射率大于周围介质，强激光聚焦下，涡旋光束对二氧化硅粒子有力学效应，不仅可以捕获微粒，还可以使微粒旋转，因而得名“光学镊子”或“光学扳手”.同时，由于光束中心光强为零，最大程度减小了对粒子的损伤，常用于捕获活体细胞、微生物等，促进了光捕获、光操纵技术的发展.下面，分别利用涡旋波片和空间光调制器产生涡旋光束，通过光镊装置，实现对SiO2微粒的捕获和旋转.

3.1基于涡旋波片的光镊实验涡旋波片可将圆偏振的平面波转化成涡旋光束，入射光的旋性决定出射涡旋光拓扑荷的正负，当入射光为右旋圆偏振光时，涡旋光束拓扑荷值为正.当入射光为左旋圆偏振光时，涡旋光束拓扑荷值为负.本实验利用涡旋波片产生涡旋光束，并实现对SiO2粒子的捕获和旋转.

3.1.1 基于涡旋波片的光镊实验装置 光镊光路图如图22所示，半导体激光器输出波长532 nm，最大功率1 W，激光经过透镜L1和L2扩束，经过偏振片使光束有更好的偏振性，经过四分之一波片使线偏振光变成圆偏振光，旋转四分之一波片，当光束偏振方向与四分之一波片的光轴方向呈π/4夹角时，产生右旋圆偏振光；光束偏振方向与四分之一波片的光轴方向呈-π/4夹角时，产生左旋圆偏振光，再通过涡旋波片(l=18),产生涡旋光束.涡旋光束经过透镜L3和L4缩束，缩束后的光束直径等于或稍大于物镜的入瞳直径，再经过二向色镜反射进入100 倍的高倍物镜，数值孔径NA=1.3.二向色镜呈45°放置，能反射捕获光，透射照明光.三维位移平台可实现对样品室的x,y,z三轴移动，载玻片置于其上作样品室，在载玻片贴有圆孔形胶环，将二氧化硅(SiO2粒子球直径为4 μm)稀释液滴入环内，盖上盖玻片.采用LED灯作为样品的照明光源，照明光通过样品室、物镜、二向色镜、滤波片，把涡旋光捕获粒子图像信息传递给CCD.由于二向色镜并不能完全反射捕获光，从物镜反射的激光会部分透过二向色镜，并入射到CCD而影响成像质量，所以需要在反射镜后放置一滤光片滤除杂光，减小对CCD成像的影响.

图22 基于涡旋波片的光镊实验装置 L1-L4:凸透镜；L:涡旋波片；Dichroic mirror:二向色镜；Microscope objective:显微物镜； Sample stage:载物台；Sample chamber:样品室；Micro particles:微粒；LED:光源；filter:滤光片

3.1.2 基于涡旋波片的光镊实验结果 实验时首先检查用作光镊的涡旋光束，即先不加装滤光片，调节三维位移平台，在计算机上显示一个清晰的涡旋光束在物镜焦平面的图像，如图23(a)所示，光场呈圆环状分布.然后加装滤光片，再调节位移平台，在物镜焦平面处捕获到三个二氧化硅粒子，位于涡旋光场光强最大处，如图23(b)所示.旋转四分之一波片，使透射光成为右旋圆偏振光，再经过涡旋波片即可产生正拓扑荷数的涡旋光束，粒子在此涡旋光束作用下顺时针旋转，图24是粒子旋转时位置抓拍图.还可以按照上文所述的方法产生左旋圆偏振光，再经涡旋波片产生负拓扑荷数的涡旋光，则可以驱动三个粒子逆时针旋转，如图25所示.我们还尝试用涡旋光束操控四个粒子旋转，如图26所示.

图23 基于涡旋波片的光镊实验 (a) 用于粒子捕获的涡旋旋光束截面图;(b)物镜焦面受捕获的粒子

图24 三个粒子受光镊驱动顺时针旋转 (a)0时刻粒子位置;(b)1.3s时粒子位置;(c)3.3s时粒子位置

图25 三个粒子受光镊驱动逆时针旋转 (a)0时刻粒子位置;(b)1.8s时粒子位置;(c)3.6s时粒子位置

图26 四个粒子受光镊驱动顺时针旋转 (a)-(c)分别为0、1.7s、3.8s、5.4s时的粒子位置

3.2全息涡旋光镊利用空间光调制器，通过编码设计涡旋全息相位图，产生涡旋光束并应用于光镊技术，实现对二氧化硅粒子的捕获旋转.

3.2.1 全息光镊的实验装置 实验装置如图27，半导体激光器输出波长532 nm，最大功率1 W，激光经透镜L1和L2扩束，照射到空间光调制器，空间光调制器加载有拓扑荷数l=30的涡旋相位全息图，用此法代替图22中的涡旋波片获得涡旋光束，再经过4f滤波系统，得到涡旋光场.光镊部分光路图与图26所示的光镊部分相同，最终由CCD接收涡旋光操控粒子的图像，并显示于计算机屏幕.

图27 全息光镊实验装置 L1、L2:扩束系统;SLM:空间光调制器;L3、L4:4f滤波系统;A:光阑;Dichroic mirror:二向色镜; Microscope objective:显微物镜;Sample stage:载物台;Sample chamber:样品室；Micro particles:微粒；LED:照明装置; filter:滤光片

图28 全息光镊实验结果 (a)0时刻粒子位置；(b)3s时粒子位置;(c) 7s时粒子位置

3.2.2 全息光镊实验结果 图28展示了全息法产生涡旋光束并操纵二氧化硅粒子旋转的实验结果，同样实现了粒子在环形光阱中的捕获和旋转.以上两次实验表明，两种方法产生的涡旋光束均可用于光镊技术.

4 结 语

本文研究了二维、三维涡旋阵列光场设计与产生，涡旋光束在光镊方面的应用，并通过实验获得了与理论模拟相一致的结果.设计制作了基于阵列涡旋光束的单环、双环晶格光场，并通过数值模拟分析了光强和相位分布的特点.发现涡旋光束叠加的数量、拓扑荷的正负决定单环还是双环晶格，拓扑荷之差决定光环晶格光场中亮暗光斑的数目.研究了呈线性排列、矩阵排列、径向排列的二维阵列涡旋光场，设计了实验光路，从实验上获得了与模拟结果相符的二维阵列涡旋光场.利用二维周期阵列光场与沿z轴传播的平面波相干涉，设计产生了多种三维阵列光场，研究发现，三维光场的类型与干涉光束的拓扑荷数有密切关系，不同拓扑荷下三维光场具有不同的类型.三维涡旋阵列光场结构分布密集，可以提供多光阱，具有广泛的应用.此外，我们利用涡旋波片和全息技术两种方法产生涡旋光束，并用于光镊实验，成功实现对多个SiO2粒子的操控与旋转，这启发我们在未来的应用中，寻找更为便捷高效的光镊技术手段，提高工作效率，降低实验成本，单涡旋光镊实验为阵列涡旋光镊的研究与应用打下了基础.涡旋阵列光束具有多个光学涡旋，按照不同排列方式呈周期性分布，比单涡旋光束增加了空间分布这一维度，不仅能增强信息传输容量，还能在光镊中增加微粒捕获和观察的数量.未来的研究工作，将完善现有的光镊系统，引入二维、三维涡旋阵列光场，进行多光阱、多粒子的三维捕获与操控.本文的研究将为阵列涡旋光场产生与应用、涡旋光及其光镊技术等领域提供参考.