一种空间信号误差异常检测分析方法

汪冬瑾 张 舒 刘 健 吴 亮 徐顺帆

1.宇航控制技术国家级重点实验室，北京 100854 2.北京航天自动控制研究所，北京 100854

0 引言

随着卫星导航系统精度的不断提升，为了进一步满足用户对系统高可靠性服务的需求，需要监测系统提供信息的正确度。监测体系根据导航系统组成，可分为空间段、地面段和用户段[1]。

空间段信号异常是影响用户定位精度的主要误差源之一[2]，它将直接导致系统信号不可用，即导致导航信息不能正确反映卫星的真实状况或者导航信号出现问题，引起用于定位的伪距误差出现突变。因此，建立有效空间信号异常检测方法，确定空间段异常的特性和成因，可为正在建设的北斗系统空间信号误差异常检测方法和完好性监测系统提供一定的借鉴[3-4]。

本文提出空间信号误差异常检测分析方法，建立了有效拟合模型，确立了异常值门限，用实测数据验证了方法的有效性，并在此基础上分析了几种异常因素的分布概率。

1 空间信号误差特性分析

卫星空间段误差主要包括卫星轨道误差、卫星钟差及相对论效应。其中，相对论效应是指由于卫星钟在地面和进入轨道后的运动速度和重力位不同而引起的卫星钟和接收机钟之间产生相对钟差的现象[2]。该误差为系统固定误差，可消除。本文讨论的是卫星轨道误差和卫星钟差，合称为空间信号误差。

用户实时定位所用的广播星历为一种地面监测站上传的预报轨道数据和星钟信息[5]，由于卫星实际运动过程中受到多种摄动力的影响，预报轨道和精密轨道存在一定的误差，且高精度原子钟存在漂移，因此广播星历存在一定的误差[5-6]。

1.1 数据提取与处理

采取国际地球动力学服务机构(International Geodynamic Service, IGS)提供的事后SP3格式精密星历作为轨道和星钟真值，经实测，精度为5cm左右[7]。空间信号误差可表征为RENIX格式brdcdd0.yyn型广播星历的轨道参数和摄动项参数依据接口文档提供的公式，解算出的地心地固坐标系(ECEF)下轨道信息和钟差信息，与同历元时刻精密星历的轨道信息和钟差信息的差值。

SP3格式精密星历间隔15min给出卫星在ITFR(International Terrestrial Reference Frame)系下的三维轨道信息及卫星钟改正数信息[7]。由于异常为小概率事件，因此取定历元间隔为1min，对精密星历内插，使得单星每年的样本数从35040扩大至525600。为避免龙格现象，同时综合考虑精度和高阶引入的计算代价，本文采用12阶拉格朗日插值法，将待插值节点位于插值区间的中部，即取位于待插值节点前6组和后6组精密星历数据作为插值区间[8]。

1.2 空间信号误差特性

目前，GPS系统在轨卫星类型可分为IIA、IIR、IIR-M和IIF型。考虑到不同类型卫星的性能和发射时间不同，可能会影响相应的空间信号误差精度。本文分别对上述4种类型的卫星分类进行分析。限于篇幅，仅给出IIR型PRN28卫星在2016年3月27日至2016年4月2日期间，ECEF中的空间信号误差的仿真结果，如图1所示。X、Y轴分别代表时间和误差(m)。

图1 PRN28卫星空间信号误差(2016.3.27-2016.4.2)

由图1可得出如下结论：轨道误差呈周期性变化；轨道误差量级为3m左右，与卫星类型关联较小；星钟误差无明显规律性。

2 空间信号异常率分析方法

2.1 轨道误差和星钟误差拟合模型

卫星以恒定角速度绕地球周期旋转，卫星轨道误差受到卫星自身轨道周期、地球公转、自转周期、日月引力等影响，必然存在一定的周期性。若周期性序列不平稳，直接用此建模会引起虚假回归问题，因此可以将轨道误差去除周期项，转换为平稳序列后，再运用平稳过程的理论和分析手段建模[9-10]。因此考虑采用最小二乘法拟合轨道误差的主要周期项；对于轨道误差剩余的非周期项和其他非主要周期项以及星钟误差，可近似看作随机量，使用自回归模型拟合。

2.1.1 最小二乘法

卫星轨道误差序列可用傅里叶展开法进行逼近：

(1)

式中，a0和b0表示长期变化的常数项和系数项，p为主要周期项个数，Ti为对应周期项的周期。ai和bi表示Ti周期项的正弦和余弦项系数，εi为非周期残差。

误差序列的频谱分析就是在频率分布区间[f1,f2]内，按照一定的频率间隔Δi逐点采样，得到n个频率采样点。其次对各采样点频率及周期，用参数拟合法，求出采样点频率f对应周期项的正余弦项系数。然后在n个采样点上，得出一组频率与周期项系数和εi的对应关系。

在频率区间[f1,f2]内，计算频率采样点

(2)

计算第i个频率采样点的拟合周期

(3)

采用最小二乘拟合法，得到所对应周期项的正余弦项系数。式(1)可表示为矩阵形式：

x=Ha+e

(4)

(5)

未知参数向量的最小二乘估计值为：

(6)

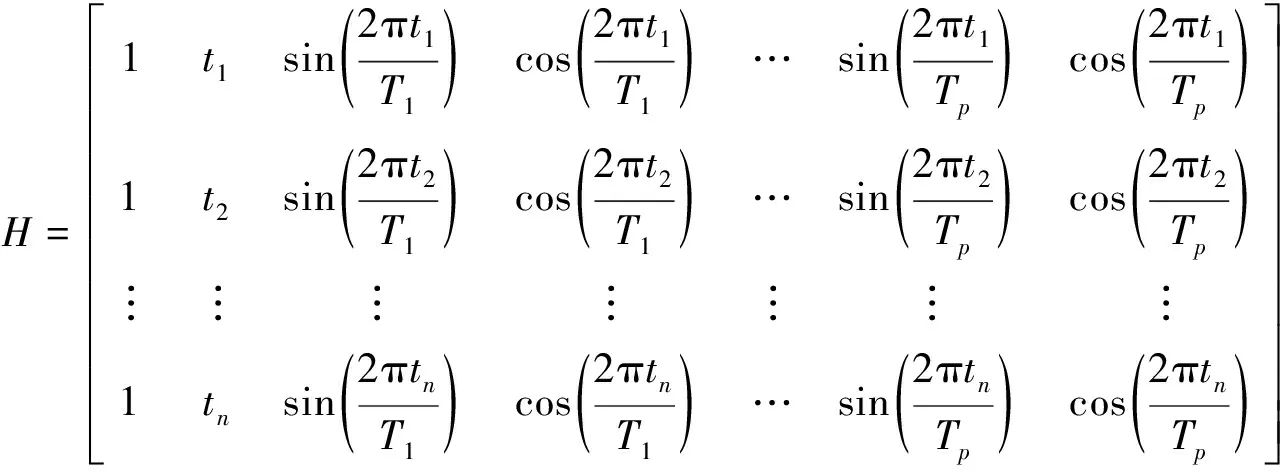
(7)

限于篇幅，只给出PRN28卫星2016年5月21～27日期间的轨道误差序列在ECEF坐标系中频谱图，如图2所示。

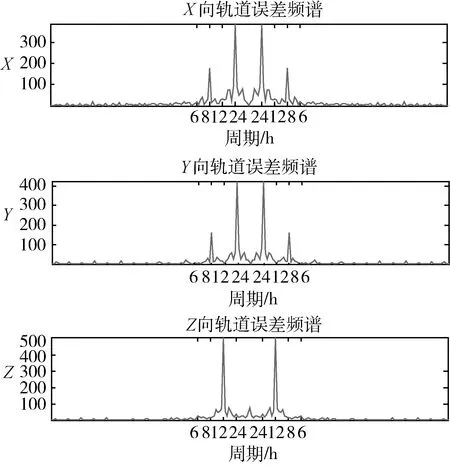
图2 ECEF中卫星轨道误差频谱图

由图2可知，X，Y和Z方向轨道误差的主要周期项分别为24h，8h和12h。

2.1.2 自回归模型

对于上述轨道误差非周期项残差序列和星钟误差序列，可近似看作平稳随机序列[10]，本文采用自回归模型拟合，以X方向轨道误差序列为例：

x(ti)=b1x(ti-1)+b2x(ti-2)+…+
bnx(ti-n)+εi

(8)

式中，bi(i=1,2,…,n)为系数项，n为自回归模型阶数，εi为拟合残差。矩阵表达形式为：

(9)

则未知参数向量的最小二乘估计值为：

(10)

采用自回归模型时，必须考虑到阶数的确定。自回归模型常用的判别准则为FPE(最终预报误差准则)，可表示为：

(11)

式(11)中，V为自回归模型残差的方差，判别准则与阶数的关系如图3所示。

FPE准则仅仅是对自回归模型精度的定性衡量，为定量衡量自回归模型阶数对拟合精度的影响，引入均方差改进量概念。设拟合前后的均方差分别为σ1和σ2，则均方差改进量R定义为：

(12)

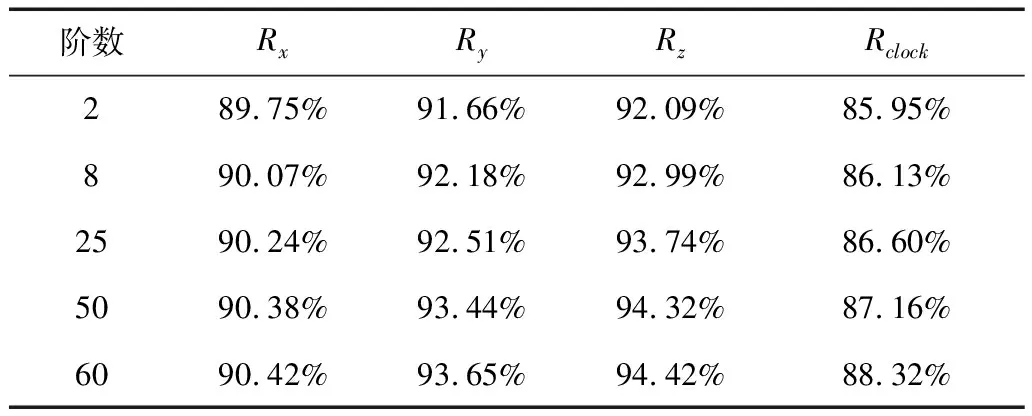
表1 均方差平均改进量与阶数对应关系

表1给出了均方差平均改进量与阶数对应关系，2阶自回归模型的改正效果为90%左右，轨道误差拟合残差仅为0.2m；星钟误差拟合残差为0.5m。星钟跳变导致均方差改进量的降低，实际中亦不能预测出星钟跳变，因此上述拟合模型基本能满足需求。随着自回归模型阶数增加，拟合改正效果逐渐增加，但计算量会显著提升，综合考虑计算代价和改正效果，取定自回归模型阶数为2阶。

2.2 异常值门限设定

为了便于综合分析卫星轨道误差和星钟误差对用户定位结果的影响，通常将空间信号误差的影响投影到观测站至卫星的距离上，计算相应的空间信号测距误差(SISRE，Signal-In-Space range error)。由卫星在覆盖范围内的平均测距误差经验公式，ESISR可用式(13)表示[11]：

(13)

式中，R,A和C分别为卫星轨道误差矢量投影到卫星惯性坐标系下的径向、切向和法向的轨道误差，T为卫星星钟误差。

将由基于傅里叶级数的最小二乘法和自回归模型拟合得出的轨道误差、自回归模型拟合得到的卫星钟误差，计算对应的ESISR作为均值，定义当实际ESISR与均值的比例超过4.42倍门限值时，则视该历元时刻空间信号误差存在异常。

3 实测空间信号验证结果及结论

为了验证上述空间信号误差异常检测方法的有效性，分析了2013年至2017年期间GPS系统不同类型在轨卫星的空间信号异常率，结果如表2所示。

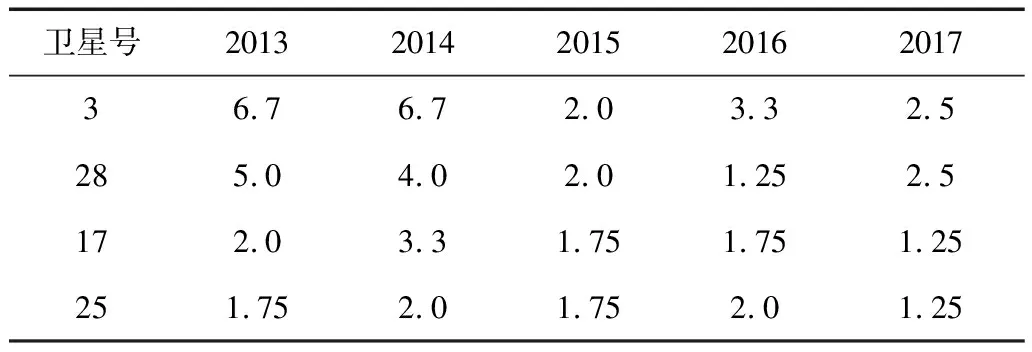
表2 GPS卫星2013～2017年空间信号异常率 [单位： 1×10-5/h]

针对空间信号常见异常因素主要包含广播星历缺失、广播星历重复播发、卫星不健康这3个方面。卫星的异常因素所对应的年度异常率(仅以PRN3号卫星为例)如表3所示。

表3 PRN3卫星异常因素统计结果 [单位：1×10-5/h]

4种类型卫星的异常率均为10-5/h左右，鉴于广播星历缺失和重复这2个异常因素有可能是由监测站数据处理引起，因此空间信号本身的异常率应低于10-5/h。与GPS系统官方公布的卫星主用服务故障指标相符[11]，验证了算法的可行性。另外，还可以得出如下结论，空间信号误差的异常率随着使用年限的增长逐渐减少；IIF型卫星异常率低于另外三类卫星，星钟性能显著提高。上述结论与实际情况相符合，也从侧面验证了异常率分析方法的有效性。

4 结论

为实现对空间段信号的异常检测，本文基于对卫星轨道误差和卫星钟误差特性的分析结果，提出了一种空间信号误差异常检测分析方法，并使用GPS系统5年实测数据验证了上述空间信号异常率分析方法的有效性。另外还得出如下结论；1)空间信号误差的异常率逐渐降低；2)IIF型卫星性能较前3种更为优异。可以期待的是能提升未来导航系统监测站的数据处理能力，发射性能更加优异的新型卫星，进一步降低空间信号的异常率。