基于平滑变结构卡尔曼滤波的机载组合导航算法*

高春雷 赵 宾,2

1.南京航空航天大学金城学院，南京 211156； 2.南京航空航天大学自动化学院，南京 211106

0 引言

捷联惯导系统(SINS)具有短期精度高、自主性高、抗干扰能力强等优势，但受其工作原理所限，误差随时间逐渐积累，长期稳定性较差[1]；全球卫星导航系统(GNSS)具有长期精度高的优点，然而在使用时易受到环境和人为干扰，定位、测速精度严重下降，无法保证持续导航定位的能力[2]。SINS和GNSS的信息具有互补性，将二者结合构成组合导航系统可实现优势互补[3]，实现无人机的自主导航。

在SINS/GNSS组合导航中，常采用卡尔曼滤波器实现对导航误差的最优估计和修正。卡尔曼滤波器是一种最优估计技术，但是其要求系统的数学模型精确，且系统噪声和量测噪声均服从高斯分布，否则滤波的精度将下降甚至发散[4]。

为克服卡尔曼滤波器对噪声的严格高斯假设，国内外学者提出了高斯和滤波器，利用高斯和对非高斯概率分布进行建模[5]，但是此方法增加了滤波器的计算复杂度。

近年来，滑模控制的思想被广泛应用到控制领域。文献[6]提出了基于解耦的变结构自适应滑模控制方法，实现了火箭全向发射下的姿态稳定；文献[7]提出一种新型的平滑估计器，解决了微小卫星主动绕飞时经典卡尔曼滤波算法存在的估计值抖动和反转问题。

采用滑模控制的策略，通过系统先验知识设定状态估计的边界，可用来提高对模型失配和非高斯噪声鲁棒性。平滑变结构(Smooth Variable Structure Filter, SVSF)算法就是基于此思路，采用滑模控制概念，通过变结构的增益，使得预测状态逐步接近真实状态[8]，对于系统模型失配以及噪声不符合高斯分布的情况具有较好的鲁棒性和稳定性。

本文以机载捷联惯导系统为应用对象，将滑模控制的思想引入到SINS/GNSS组合导航中，研究基于卡尔曼的平滑变结构滤波器，克服常规卡尔曼滤波算法对系统模型和噪声特性的限制，提高组合导航的鲁棒性。

1 平滑变结构卡尔曼滤波算法

如图1所示随时间变化的系统状态的轨迹，基于SVSF理论，估计状态是通过系统的不确定模型得到的，通过SVSF增益的选取，可使得估计状态轨迹朝着系统状态轨迹逼近，直至进入到存在子空间以内，然后估计状态被限制在存在子空间内时，沿着系统状态轨迹来回的切换[9-11]。存在子空间始终围绕着真实的系统状态轨迹，其宽度包含了干扰和不确定性。如果干扰和不确定性是有界的，就可以得到存在子空间宽度的界限。因此，SVSF算法对系统模型和噪声模型不准确的情况具有较好的鲁棒性和稳定性。

图1 SVSF估计的基本思想

本文采用基于协方差的线性离散系统迭代方程，研究基于平滑变结构卡尔曼的组合导航滤波算法。

设线性离散系统具有如下的状态方程以及量测方程：

(1)

式中：Xk表示k时刻的系统状态向量(n维)；Zk表示k时刻的量测向量(m维)；Φk/k-1表示由k时刻到k+1时刻的一步状态转移矩阵，大小为n×n阶；Wk表示k时刻的系统噪声向量；Hk是k时刻的量测系数矩阵，大小为m×n阶；Γk表示系统噪声系数矩阵；Vk表示k时刻的量测噪声向量(m维)。

平滑变结构卡尔曼滤波迭代方程如下：

1)通过系统模型计算一步预测状态估计

(2)

2)计算一步预测状态估计协方差矩阵

(3)

式中：Qk-1为系统噪声协方差阵。

(4)

4)根据实际量测值和预测量测值，计算先验量测误差变量ez,k/k-1

(5)

5)根据噪声信息和误差信息计算SVSF增益

(6)

其中diag(v)表示以向量v的各元素作为主对角线元素，构造对角矩阵；|e|表示对向量e中的各元素取绝对值，得到与e维数相同的向量；“∘”表示Hadamard乘积；S是对先验量测误差列向量ez,k/k-1中各元素进行饱和运算后得到的与ez,k/k-1维数相同的列向量，其各元素的饱和运算定义如下：

(7)

其中，ezi,k/k-1为先验量测误差列向量ez,k/k-1的第i个元素，ψkii为平滑有界宽度阵ψk的第i个对角线元素，二者相除构成饱和运算得到的列向量S的第i个元素。平滑有界宽度ψk可以减小由于滤波增益高频切换引起的状态估计的抖振，

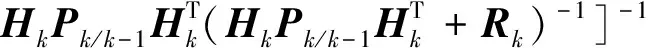
(8)

式(8)中，Rk为量测噪声协方差阵。

通过式(7)饱和运算，在有界宽度外，可保证估计的鲁棒性和稳定性，在有界宽度内，可通过插值获得平滑函数。

由式(6)可以看出，SVSF增益是一个函数，它与先验量测误差变量ez,k/k-1、后验量测误差变量ez,k-1/k-1、平滑有界宽度ψk、记忆因子γ(0<γ<1)以及量测矩阵Hk有关。

6)由一步预测状态估计和SVSF增益计算状态估计

(9)

7)计算状态估计协方差矩阵

(10)

8)最后，更新后验量测误差变量ez,k/k

(11)

2 基于平滑变结构卡尔曼滤波的组合导航方案设计及系统模型

2.1 组合导航方案设计

以机载捷联惯导系统为组合导航研究对象。在组合导航过程中，利用捷联惯导系统解算的位置、速度与GNSS测得的位置、速度之差作为量测信息，用本文提出的平滑变结构卡尔曼滤波器对捷联惯导系统的各项误差信息进行估计，滤波过程中对惯导系统实时进行闭环校正。基于平滑变结构卡尔曼滤波的SINS/GNSS组合导航方案如图2所示。

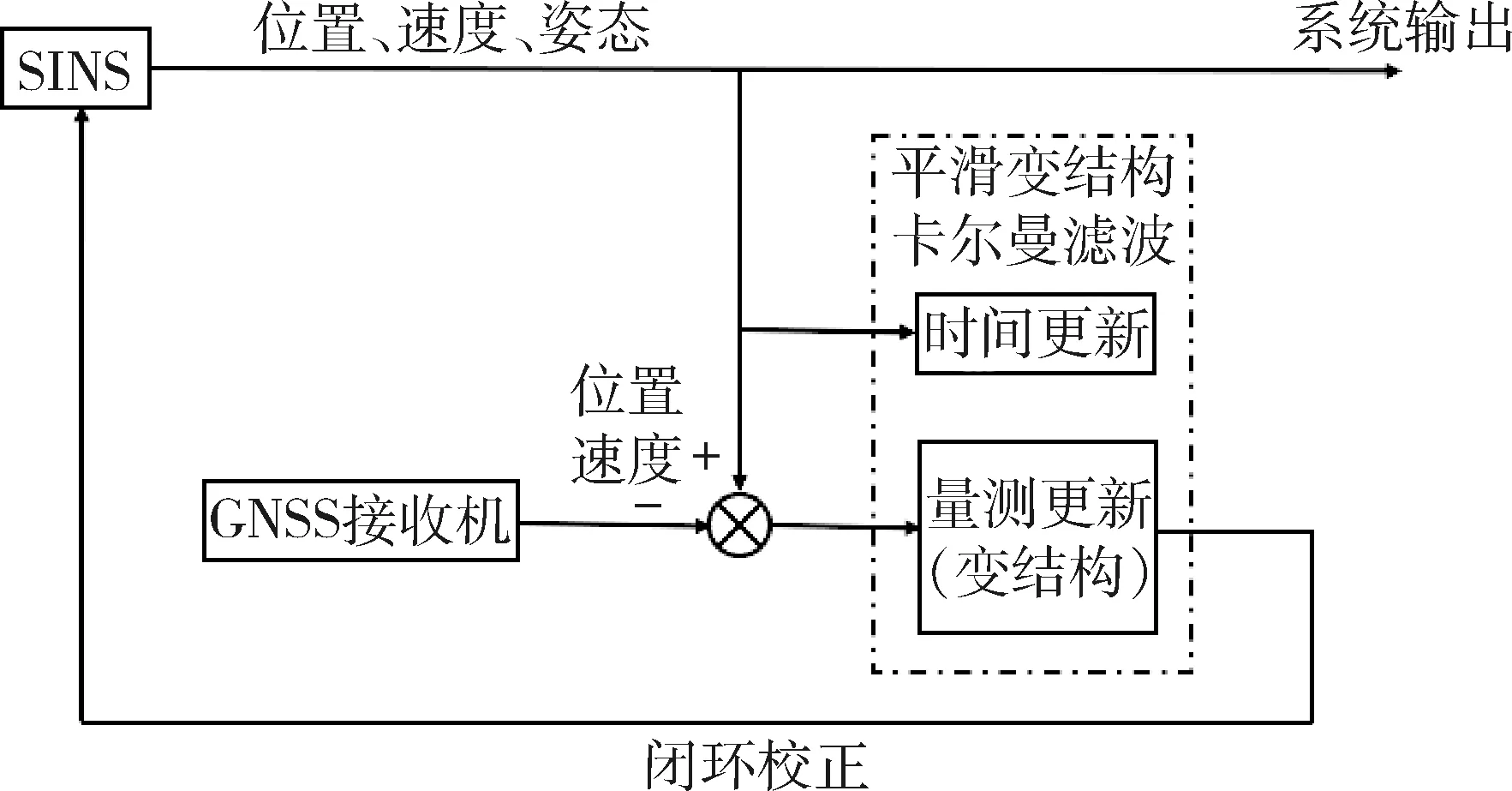
图2 基于平滑变结构卡尔曼滤波的SINS/GNSS组合导航方案框图

2.2 组合导航系统模型

1)组合导航系统状态方程

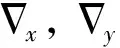
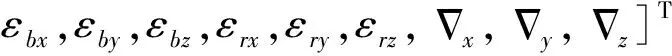
通过对SINS系统性能和误差源的分析，即可得到组合导航系统状态方程：

(12)

式中：X(t)为系统状态向量；Φ(t)为状态转移矩阵；Γ(t)为系统噪声系数矩阵；W(t)为系统噪声向量。

2) 组合导航系统量测方程

以捷联惯导系统导航解算得到位置、速度和卫星导航系统测量得到位置、速度的差值作为量测信息，则SINS/GNSS组合导航滤波器量测方程为：

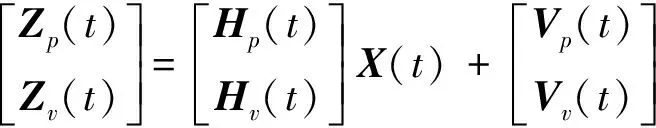
(13)

式中：H(t) 为量测系数矩阵，Zp(t)为位置量测向量，Vp(t)为位置量测噪声向量，近似为白噪声；Zv(t)为速度量测向量，Vv(t)为速度量测噪声向量，近似为白噪声。

对式(12)、(13)进行离散化处理，可得到式(1)形式的线性离散系统模型，通过平滑变结构卡尔曼滤波器即可进行滤波估计，实现机载SINS/GNSS组合导航。

3 基于平滑变结构卡尔曼滤波的组合导航算法仿真验证分析

3.1 仿真条件

1)仿真参数设置见表1所示。

表1 仿真参数表

2)系统仿真时间600s,包含了爬升、平飞、加速、减速、转弯的过程。

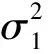
为验证平滑变结构卡尔曼滤波算法的鲁棒性，在100～200s设置测速干扰，假定受到干扰的GNSS速度量测噪声服从以下非高斯分布[13]：

(14)

其中，σ1为理想情况下的GNSS量测噪声标准差，仿真中设置为0.2；σ2为异常干扰噪声标准差，通常取值较大，仿真中设置为σ2=50σ1；ε为扰动比例因子，仿真中设为0.3。

3.2 仿真分析

在上述仿真条件下，采用本文研究的平滑变结构卡尔曼滤波算法对机载组合导航系统进行导航解算，选择仅采用卡尔曼滤波组合导航方法作为对比进行分析验证。滤波过程中对惯导系统进行闭环校正，通过误差校正后的导航参数与理想参数作差(即误差值)对比分析。两种滤波算法的组合导航位置误差曲线、速度误差曲线分别如图3～4所示。

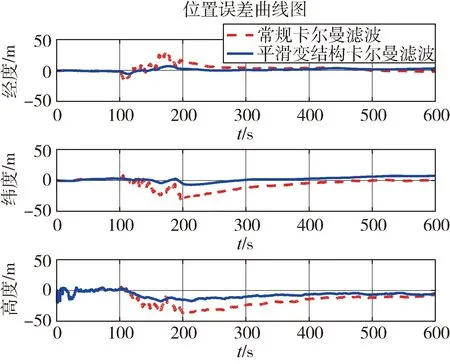
图3 两种滤波算法的位置误差曲线

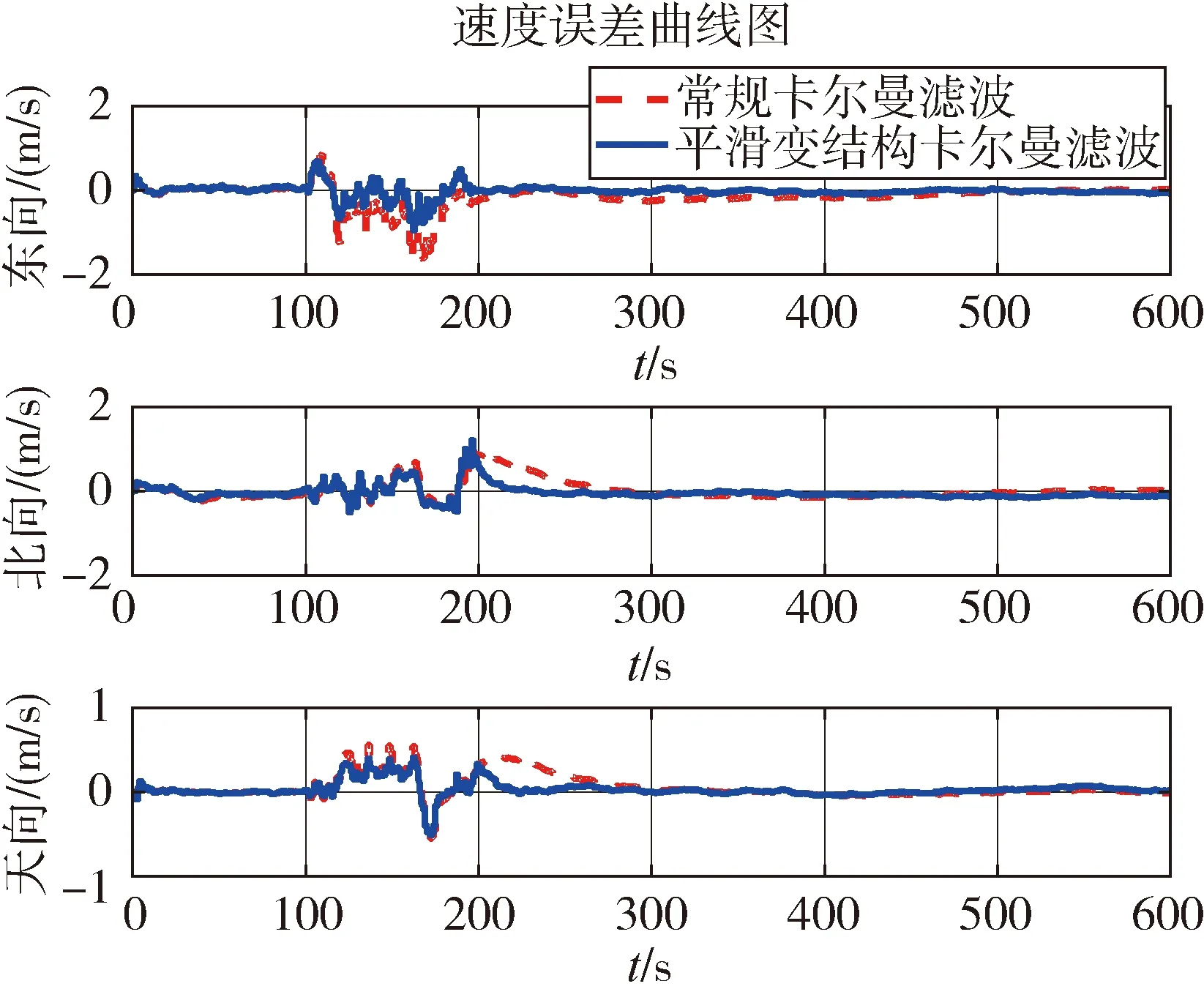
图4 两种滤波算法的速度误差曲线

对两种滤波方法的位置、速度误差进行统计分析，两种滤波方法的位置、速度误差绝对值的均值以及误差的标准差如表2所示。

表2 两种滤波方法误差绝对值的均值和误差标准差

由图3～4可以看出：在0～100s，GNSS速度量测噪声尚未受到干扰时，本文研究的平滑变结构卡尔曼滤波器和常规卡尔曼滤波器的性能基本一致，均具有较好的精度；在100～200s，GNSS速度量测噪声如式(14)所示，受到异常噪声干扰，不再符合高斯分布，此时常规卡尔曼滤波精度下降，速度和位置误差均受到较大影响。而平滑变结构卡尔曼滤波器采用变结构增益的思想，具有一定的鲁棒性，速度精度优于常规卡尔曼滤波，位置精度有较大幅度的提升；在200s干扰结束后，常规卡尔曼滤波的估计误差需要较长的收敛时间，而平滑变结构卡尔曼滤波的估计误差很快收敛到正常情况下的精度。

从表2的统计结果也可以看出，在GNSS受扰、量测噪声异常的情况下，本文研究的平滑变结构卡尔曼滤波算法在估计精度、鲁棒性以及稳定性方面均优于常规卡尔曼滤波算法。

4 结论

为改善卡尔曼滤波算法性能、提高机载SINS/GNSS组合导航系统的鲁棒性，研究了一种基于卡尔曼的平滑变结构滤波算法。在量测噪声非高斯分布情况下，验证该方案的可行性及组合导航对准性能。仿真验证结果表明，在GNSS测速性能未受扰情况下，本文研究的平滑变结构卡尔曼滤波和常规卡尔曼滤波性能一致；在GNSS受到干扰、速度量测噪声不符合高斯分布的情况下，平滑变结构卡尔曼滤波算法在估计精度、鲁棒性以及稳定性方面均优于常规卡尔曼算法，且在干扰结束后能快速收敛到正常情况下的精度。平滑变结构卡尔曼滤波算法克服了常规卡尔曼滤波算法对系统模型和噪声特性的限制，对工程应用具有重要的参考价值。