基于因子分析法的路面技术状况评价指标体系CPF构建

徐 霈，李家龙，李 聪，邓卫东

(1.招商局重庆交通科研设计院有限公司，重庆 400067； 2.国家山区公路工程技术研究中心，重庆 400067；3.山区道路工程与防灾减灾技术国家地方联合工程实验室，重庆 400067；4.重庆奉建高速公路有限公司，重庆 404699)

“数据丰富与知识贫乏”是当今信息时代人类面临的突出问题，“向数据要知识”的数据挖掘与知识发现研究成为近年来人工智能AI(Artificial Intelligence)与大数据BD(Big Data)领域研究的重心与热点。对道路结构开展全面、准确评价是有效实施智能管养的基础条件，而目前行业内主流检测(监测)方法或手段所得数据，具有数量大、维度高、信息交叉等特点，即“富数据—贫知识”矛盾突出，这给合理评价道路结构在役技术状况带来了极大的挑战。目前路面质量评价存在指标笼统、信息交叉失真，指标区分度不清晰，养护指导性不强，评价维度不全面等问题，给管养单位准确掌握道路结构在役状况、制定科学养护方案带来技术难题，不利于促进企业降本增效。

为了全面、准确地评价路面技术状况，我国研究人员在路面技术状况评价指标方面开展了大量工作，通过实测数据，采用不同的方法和模型，建立了不同的路面技术状况评价指标体系。谢峰等[1]通过模糊神经网络的方法建立了高速公路路面使用性能综合评价方法，该模型与实际路况符合性较好；潘怀兵[2]通过主成分分析方法，克服了路面性能综合评价指标权重分配的主观影响因素，使得综合评价指标更具有客观性和科学性；胡霞光[3]通过遗传算法建立了路面使用性能评价GANN模型，对权重值和阈值进行了优化，得到了较优的模型；陆键[4]通过聚类分析确定专家个体权重向量的K类划分，引入专家个体权重向量权重系数，进而得出常权系数值，提出变权模型和分组变权模型计算评价模型权重系数值；周岚[5]通过分析江苏省高速公路沥青路面损害类型，对规范确定的评价指标进行了改进，确定了江苏省高速公路沥青路面使用性能评价体系；刘文[6]建立了基于可拓理论的综合评估模型，并采用江苏京沪公路路面检测数据对该模型进行了验证，结果表明，基于可拓理论的评估模型能对路面使用性能进行准确评价，可验证该评价模型的实用性；巩建[7]利用变权原理将主观弯沉权重和客观弯沉权重相结合，建立了基于弯沉指标的沥青路面使用性能评价模型，并通过工程实例对评价模型进行应用，表明新的评价模型能够更客观、更准确地体现路面实际状况；刘圣洁[8]以集对分析理论为基础，建立了路面性能指标与路面性能各等级标准之间的联系度表达式，将集对分析联系度表达式用于路面性能评价，评价结果与路况符合性高。

现行路面使用性能评价指标尽管已被使用多年，但在实际应用中出现的问题越来越难以满足现今公路养护管理的需求，评价结果也难以为路面养护决策提供依据[9-11]。基于上述研究分析，本文拟采用因子分析方法，归并影响因素，构建个数较少的潜在因子，代替原有个数较多的表观参数(检/监测所得)，克服原始数据相关性、重叠性显著等弊端，保留其绝大部分信息，从而构建起通过少量潜在因子精准评价道路结构服役性态的全新体系。

1 因子分析基本原理

1.1 基本思想

因子分析是一种处理较多数据的方法，它通过对原始变量数据的相关关系及结构探索，用几个抽象的新变量来表示原始变量中信息的结构，新变量称之为“公因子”。原始变量是易收集的显性变量，因子则是无法直接得到的潜在变量。当变量不多时，易处理数据，甚至直观比较即可；当变量较多时，就需使用多元统计分析，采用专门的方法来减少变量，用个数较少的新变量来代替原始变量，且新变量能涵盖原始变量较多的信息，要实现这种情形则原始变量之间一般来说有一定的相关性，是一定程度上的降维处理[12-14]。

1.2 基本步骤及模型构建

因子分析法的主要步骤如下：1) 对数据样本进行标准化处理；2) 计算样本的相关系数矩阵；3) 求解相关系数矩阵的特征根、特征向量和方差贡献率；4) 根据累计贡献率确定主因子的个数；5) 计算因子载荷矩阵，并对相关因子进行命名解释。

公因子是不可直接观测但又客观存在的共同影响因素，每个变量都可表示成公因子的线性函数与特殊因子之和，即

其中：F1，F2，…，Fm称为公因子；εi称为Xi的特殊因子。该模型可用矩阵表示为：

X=AF+ε

其中：

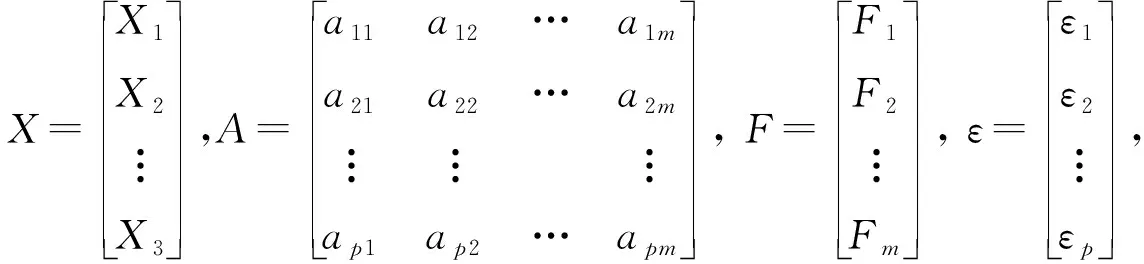
1)m≤p；

2)E(F)=E(ε)=0；

3)Cov(F，ε)=0，即公因子与特殊因子不相关；

4)Var(F)=Im，即各个公因子不相关，且方差为1；

5)Var(ε)=diag(σ12，σ22，…，σp2)，即各个特殊因子不相关，方差可以不同。

上述矩阵可以表达为：

其中各项的含义是：

1)A为因子载荷矩阵；

2)aij为因子载荷，是第i个变量在第j个因子上的负荷，如果把Xi看成m维空间中的点，则aij表示它在坐标轴Fj上的投影。

1.3 因子得分计算

因子得分是因子分析中比较重要的结果，是获取综合得分的前提。通过载荷矩阵计算各公因子在每个样本上的具体数值，同时用因子得分代替原始变量，以达到降维效果。

假设Fj对变量X1，…，Xp的回归方程为

因为Fm和Xi都已经被标准化，有

由因子载荷的统计意义可知：

aij=rX,Fj=E(XiFj)=E[Xi(bj1X1+…+bjpXp]=bj1E(Xi·X1)+…+bjpE(Xi·Xp)=bj1ri1+…+bjpripi=1,…,p

整理为：

Rbj=ajj=1,…,m

其中:

bj=(bj1,bj2,…,bjp)T，aj=(a1j,b2j,…,bpj)T,

所以有：

bj=R-1ajj=1,…,m

令：

有：

可得：

其中：X=(X1,X2,…,Xp)T。

2 模型构建及CPF结果计算

2.1 模型构建

1) 对现行技术状况评定检测数据进行KMO和Bartlett检验以及显著性水平检验，以此分析该类数据的相关性以及因子分析的适用性；

2) 通过相关性矩阵以及因子旋转抽取特征值大于1的因子，并根据因子载荷矩阵分析不同检测指标数据在所抽取因子上的权重数，据此进行因子分析模型计算和命名解释性分析。

2.1.1 路面实测指标选取

为对路面技术状况实测数据进行因子分析，选取路面技术状况各分项评价指标的原始检测数据，其中路面损坏状况指数PCI选用实际检测数据破损率、路面跳车指数PBI选用实测纵断面高差Δh计算每km代表值。路面实测数据采用云南某高速公路2019年公路技术状况指标检测数据，如表1所示。

2.1.2 相关性分析及因子分析适用性检验

为确定所选取的数据是否能够进行因子分析，需要对选取数据进行相关性分析。本文采用相关系数矩阵以及KMO和Bartlett检验，测试该数据因子分析的适用性。经KMO和Bartlett检验，其中KMO值为0.549，根据统计学家Kaiser给出的KMO度量标准可知[15]，选取的原始变量适合进行因子分析；Bartlett球度检验得出的相伴概率Sig.为0.000，小于显著性水平0.05，因此拒绝Bartlett球度检验的零假设，认为变量间存在较强的相关性，适合做因子分析。相关系数矩阵如表2所示。

由表2可知，通过相关系数矩阵对所选指标X1～X6进行相关性分析，平整度X2分别与车辙深度X3和纵断面高差X5的相关系数值为0.332和0.486，呈现出较强的相关性；路面破损率X1与实测弯沉X4相关系数值为0.580，呈现出较强的相关性；路面磨耗X6与纵断面高差X5和实测弯沉X4相关性不显著。

2.1.3 公因子提取

将采用的云南某高速公路实测数据经无量纲标准化处理[16]后进行因子分析，各个公因子的特征值、累计贡献率如表3所示。

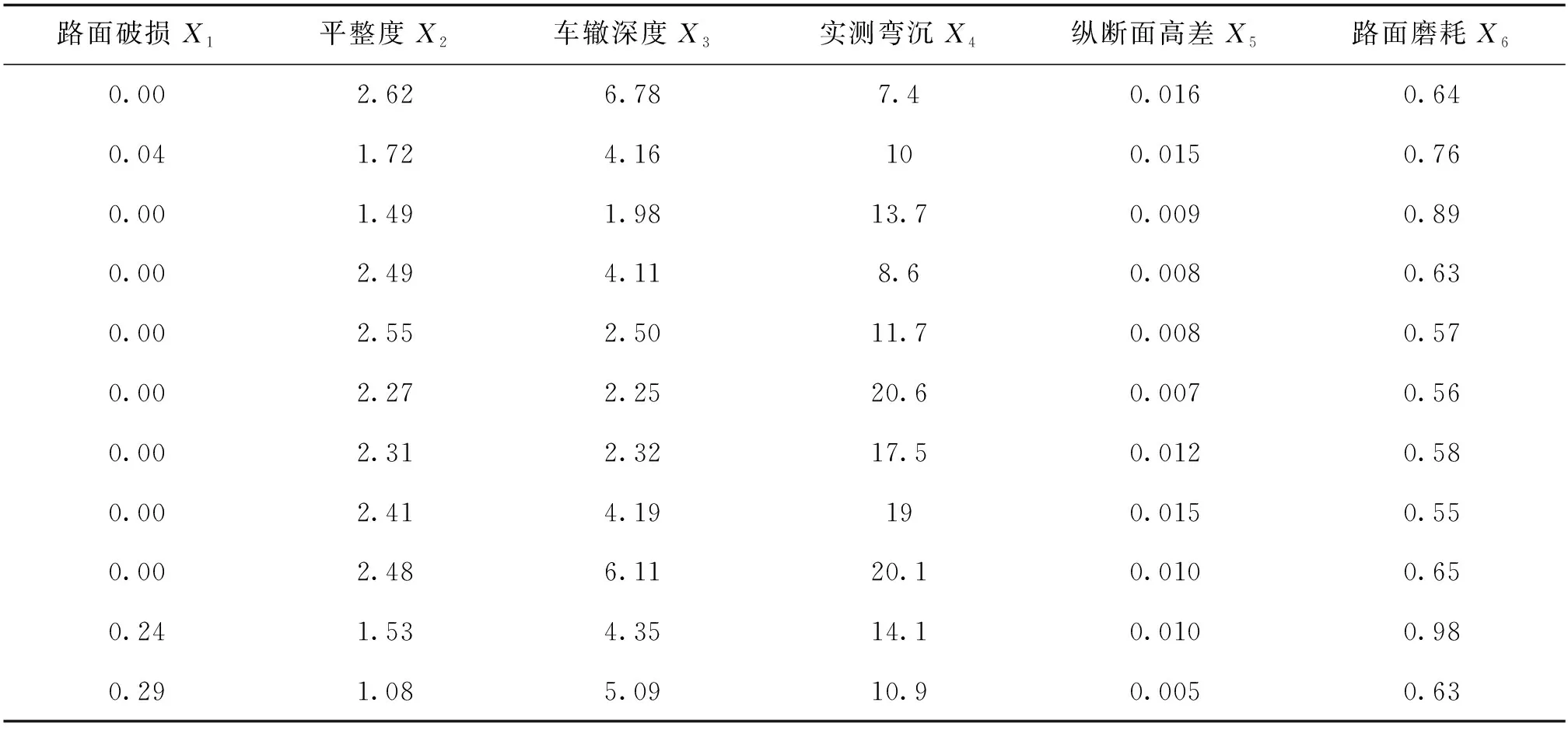
表1 云南某高速公路2019年公路技术状况检测数据汇总

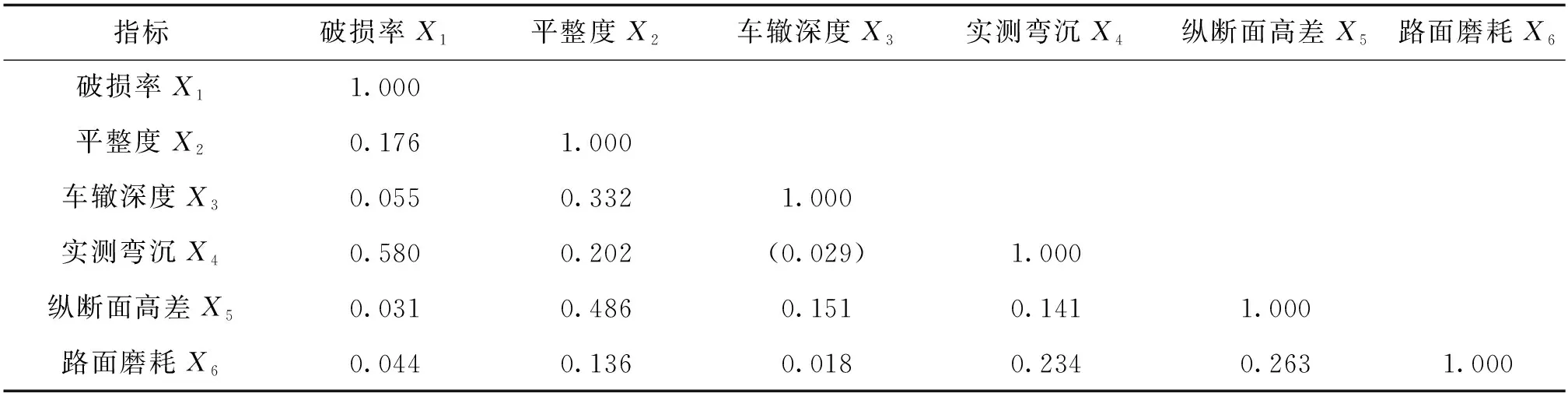
表2 相关系数矩阵

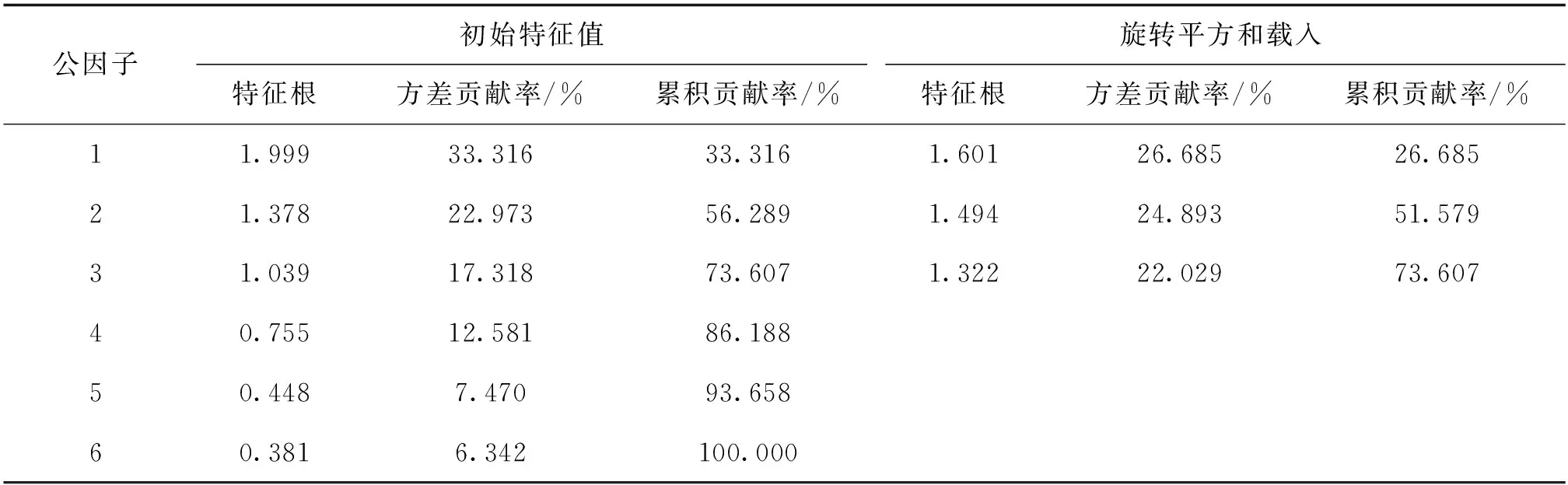
表3 公因子的特征根、贡献率和累计贡献率

由表3可知，前3个因子变量的特征值均大于1，并经过最大方差旋转后其方差贡献率分别为26.685%、24.893%和22.029%，累计方差贡献率为73.607%，说明这3个因子可把所选6个路面技术状况评定指标的较大部分信息反映出来，因此可选取这3个因子作为路面技术状况的综合评价指标。

2.1.4 因子命名解释

因子载荷矩阵是因子分析的核心计算结果，通过对提取的3个公因子进行载荷矩阵分析，得到各个指标的载荷矩阵，如表4所示。

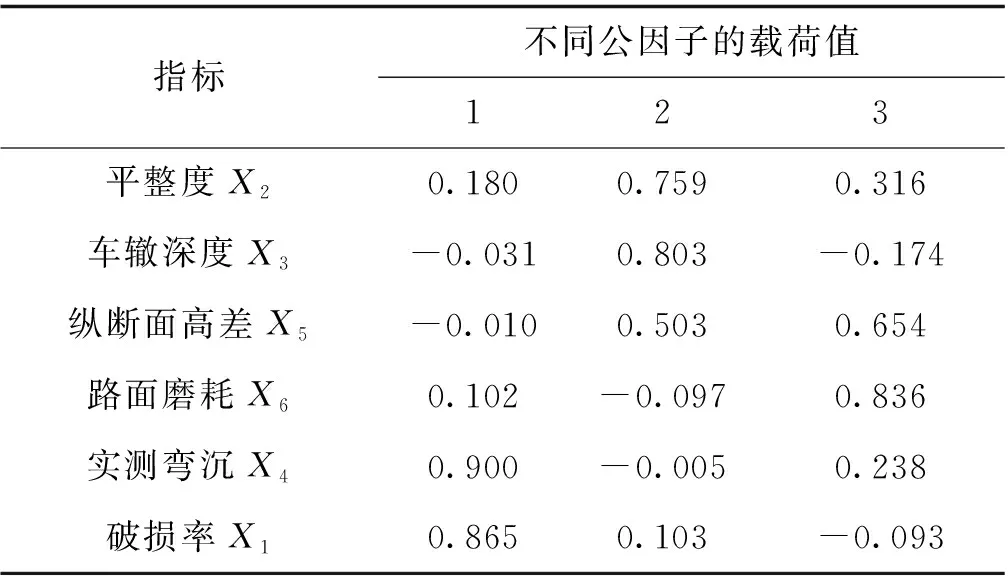
表4 各指标正交旋转后的因子载荷矩阵

由表4可知，实测弯沉X4和破损率X1在第1个因子上有较高的载荷，说明第1个因子主要解释了该2个指标，可命名为结构性能因子SPF；平整度X2和车辙深度X3在第2个因子上有较高的载荷，说明第2个因子主要解释了这2个指标，可命名为行驶舒适因子CSF；路面磨耗X6和纵断面高差X5在第3个因子上有较高的载荷，说明第3个因子主要解释了该2个指标，可命名为行驶安全因子DSF。

2.2 CPF结果计算

通过旋转后的成分矩阵得到因子的分系数矩阵，采用回归法计算因子的得分系数，如表5所示。

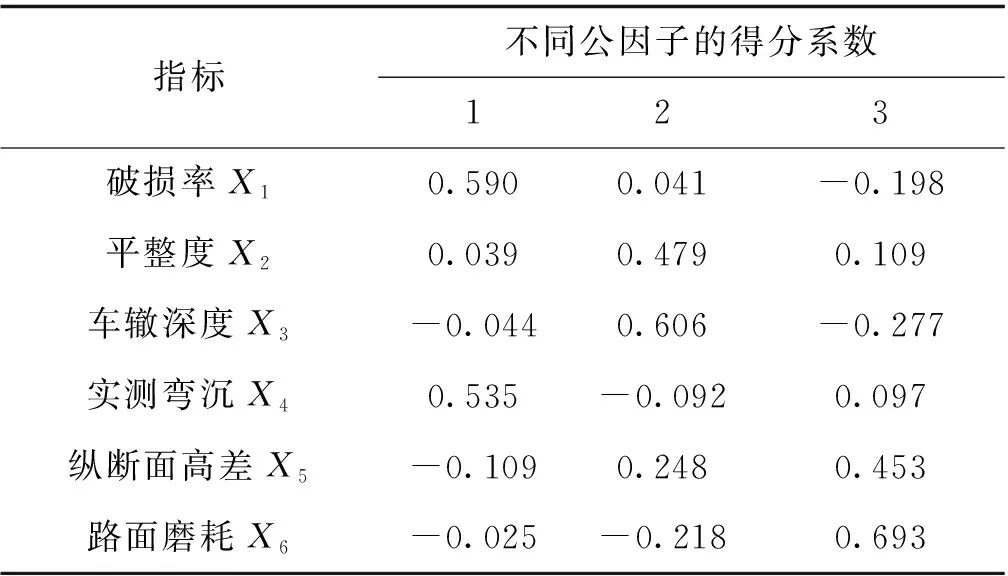
表5 因子得分系数矩阵

由表5可知，各因子得分函数如式(1)～式(3)：

SPF=0.590X1+0.039X2-0.044X3+0.535X4-0.109X5-0.025X6

(1)

CSF=0.041X1+0.479X2+0.606X3-0.092X4+0.248X5-0.218X6

(2)

DSF=-0.198X1+0.109X2-0.277X3+0.097X4+0.453X5+0.693X6

(3)

为了对高速公路全线里程逐段进行综合评价，采用计算因子加权总分的方法，以3个因子方差贡献率为权重数。因此，综合评价因子指数CPF如式(4)所示：

CPF=0.365SPF+0.338CSF+0.297DSF

(4)

3 CPF与PQI评价指标对比分析

3.1 CPF与PQI评价结果对比

通过对该高速公路的道路实测数据分别计算得出PQI和CPF，汇总后对比分析如图1、表6所示。

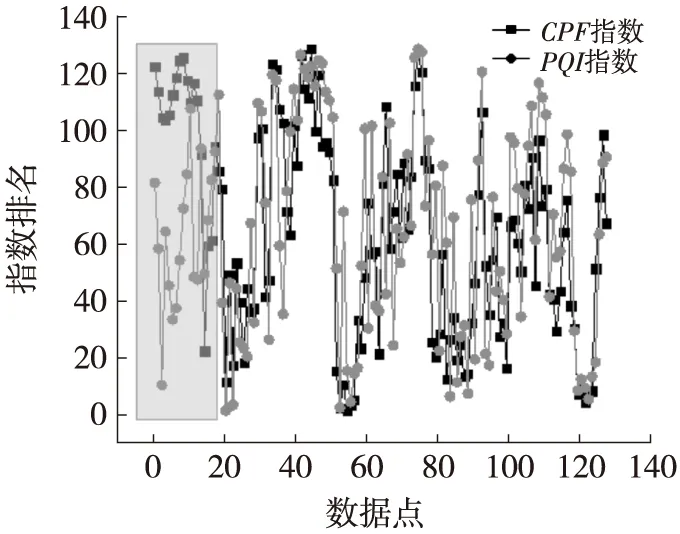
(a) 全路段CPF与PQI指数排名对比

(b) 路段0～18CPF与PQI指数排名对比

从图1可以看出，综合评价因子CPF与PQI指数排名在数据点0～20范围存在较大偏差，呈现出相反的路段综合评价结果；在数据点20以后，2种评价指标间仍然存在一定的偏差，但趋势基本接近，呈现出较一致性的路段综合评价结果。

从表6可以看出，PQI得分受PCI分值影响最大。在路段0～9间，平整度值大部分超过极限值2.3，表现出平整度较差，RQI分值较低，但此段路面破损较好，PCI分值较高，PQI分值也随之仍然较高，路段被评定为“优”；在路段10～20间，平整度均小于2.3，表现出平整度较好，RQI分值较高，但此段路面破损较差，PCI分值较低，PQI分值也随之降低，并且路段19因为路面破损PCI分值低，被评定为“良”。

综合全路段评定趋势来看，现行评价标准中以路面破损PCI为主控指标，对PQI分值和路段最终评定影响最大。但在实际养护运营管理中，平整度较差路段不仅对驾乘人员行驶舒适度影响较大，车辆的频繁颠簸还会对路面造成冲击和损伤，最终导致路面病害的发生，平整度较差路段也应根据分值评定为较差路段，从而提前进行养护维修。

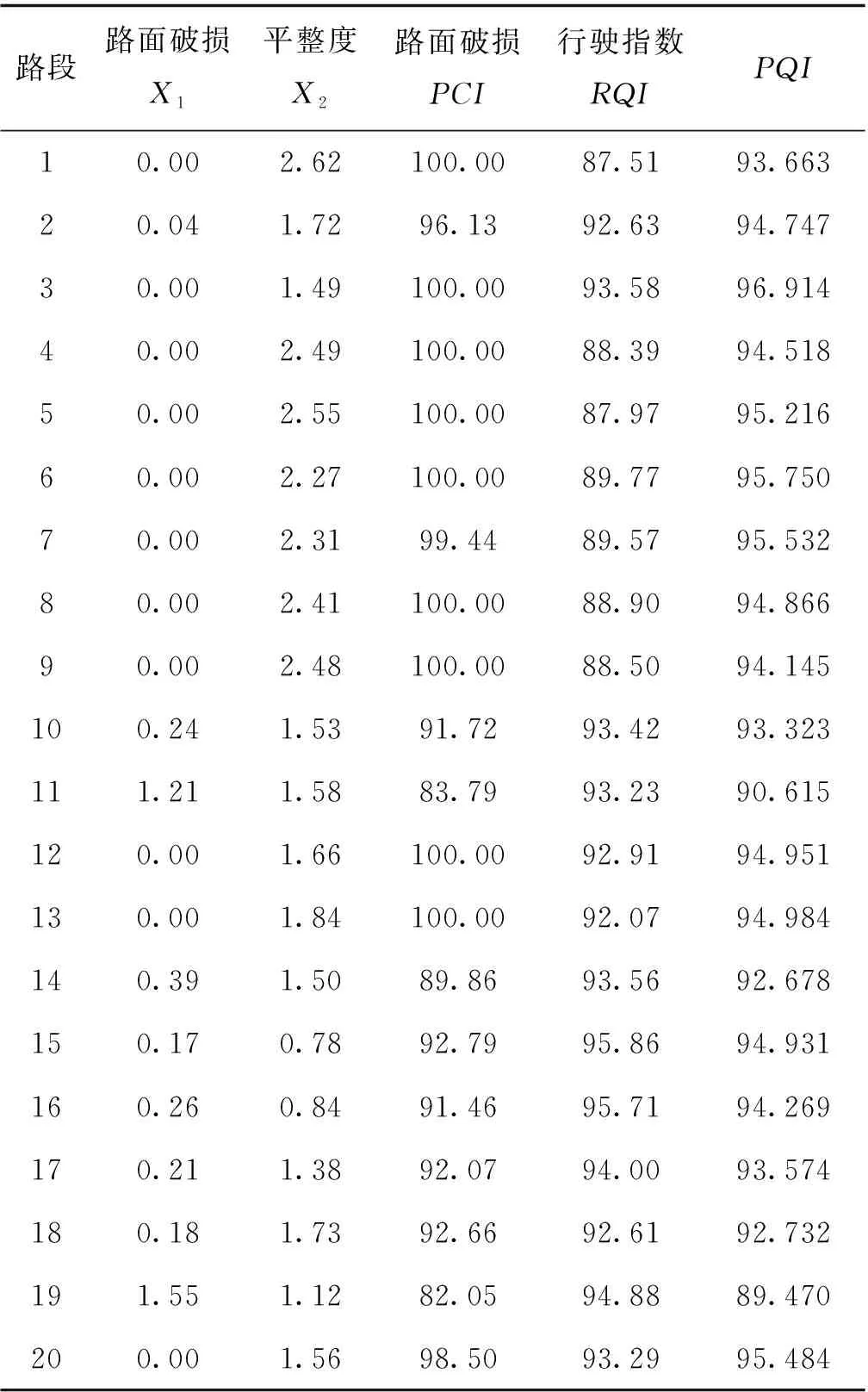
表6 路段数1～20的分项评价指标汇总

3.2 CPF和PQI评价体系对比

现有路面技术状况评价体系PQI与新构建的CPF综合评价体系的对比如图2所示。

从图2可以看出，CPF综合评价体系相比较于PQI综合评价体系分项评价指标较少，将繁杂多维度且有交叉性的分项评价指标转换为低纬度且独立性较强的分项评价指标体系，使得综合评价体系简单易懂针对性强。

根据JTG 5210—2018《公路技术状况评定标准》[17]，路面技术状况综合评定指数PQI如式(5)所示：

PQI=0.35PCI+0.30RQI+0.15RDI+0.10PBI+0.10SRI/PWI

(5)

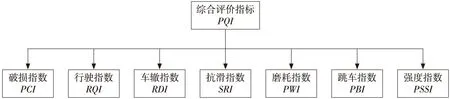
(a) PQI综合评价体系

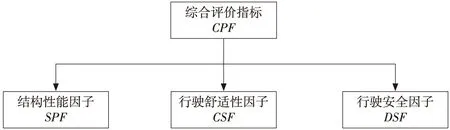
(b) CPF综合评价体系

对比公式(4)、(5)可知，相较于现行路面技术状况评价体系PQI，CPF综合评价体系将目前各分项评价指标进行关联性组合，并通过前文的权重分配系数计算，给出了相应的权重值，特别是将弯沉评价指标有效联系起来，弥补了PQI评价中无法给出弯沉权重值而导致弯沉检测被忽视的弊端。

4 结论

1) 本文采用因子分析法将现有个数较多的路面技术状况评价指标转换为个数较少的公因子，并提出了一种新的路面技术状况评价指标CPF体系，该评价体系由结构性能因子SPF、行驶舒适因子CSF和行驶安全因子DSF组成。

2) 通过CPF与现行PQI指标的对比分析，验证了因子分析方法的可行性以及CPF综合评价体系的客观性，CPF能有效弥补现行评价指标相互重叠以及弯沉权重值缺失的情况，使得评价结果更符合路面的实际状况。

3)CPF评价方法依靠实测路段的检测数据间关系进行分项评价指标间的权重分配，并通过与PQI评价结果进行对比，该权重值的确定方法具有较好的可靠性。