连续刚构桥采用屈曲约束支撑减震效果研究

郑万山，左永强，刘怀林，高文军，谢皓宇

(1.桥梁工程结构动力学国家重点实验室，重庆 400067； 2.中煤科工重庆设计研究院(集团)有限公司，重庆 400042)

预应力混凝土连续刚构桥既有连续梁无伸缩缝、行车平顺的特点，又有T型刚构桥不设支座、施工方便的优点，在50 m～200 m跨径具有很大的竞争优势[1-2]。但随着高墩连续刚构桥的应用越来越广泛，在强震山区修建连续刚构桥梁不可避免，如何提高连续刚构桥梁抗震性能是众多学者研究的热点。传统的连续刚构桥减隔震方式是在边墩或桥台处设置减隔震装置[3]。本文提出一种不同的方式，即在连续刚构的双薄壁墩上设置屈曲约束支撑BRB(Buckling Restraine Brace)来提高结构的抗震性能。

近年来，也有部分学者引入屈曲约束支撑来提升桥梁抗震性能。EI-Bahey等[4]在桥梁双柱墩上设置BRB，通过试验和模拟分析验证了BRB减震的效果。Bazaez等[5]对安装BRB后的双柱式桥墩进行了拟静力试验研究，验证了在双柱墩安装BRB可提升结构耗能能力，并给出了与墩柱连接的构造细节。Wang等[6]以1座3跨梁桥为对象，通过数值分析，验证了BRB对桥梁墩台的减震作用。孙志国等[7]通过拟静力试验和数值模拟方法，验证了BRB提升桥梁抗震性能的有效性。李晓莉等[8]对山区双柱桥墩安装BRB进行了减震效果研究，通过数值分析，发现小震下BRB可减轻双柱桥墩的地震力，但会增加基础剪力，大震下能够有效减小桥墩塑性变形和控制残余位移角。石岩等[9]对设置BRB排架墩进行了抗震设计方法研究，发展了设置BRB的桥梁排架墩基于位移的抗震设计方法。

综上分析，国内外学者研究成果主要集中在双柱墩的横桥向柱间安装BRB，并研究BRB对横桥向抗震性能的影响。由于BRB轴向刚度较大，在桥梁纵桥向应用BRB还不多见。本文以双薄壁墩连续刚构桥为对象，研究在桥墩肢设置BRB后的减震效果。

1 屈曲约束支撑原理

屈曲约束支撑是一种广泛用于建筑结构的新型支撑方法，主要由核心单元、约束单元和滑动机制单元3部分构成，如图1所示。核心单元是构件的主要受力单元，选择的材料一般是具有特定强度、低屈服点的钢材，常见的有Q235。芯板钢材的主要截面形状包括：十字形、T形、双T形和一字形，每种形状对应着不同的刚度要求和耗能机制。约束单元是普通支撑和防屈曲约束支撑的最大区别，其主要作用是防止核心单元在受力情况下先发生整体和局部弯曲。常见的约束形式是外壳内填充特定性质的混凝土，外壳常见的形式有圆形钢管和矩形外壳[10-11]。

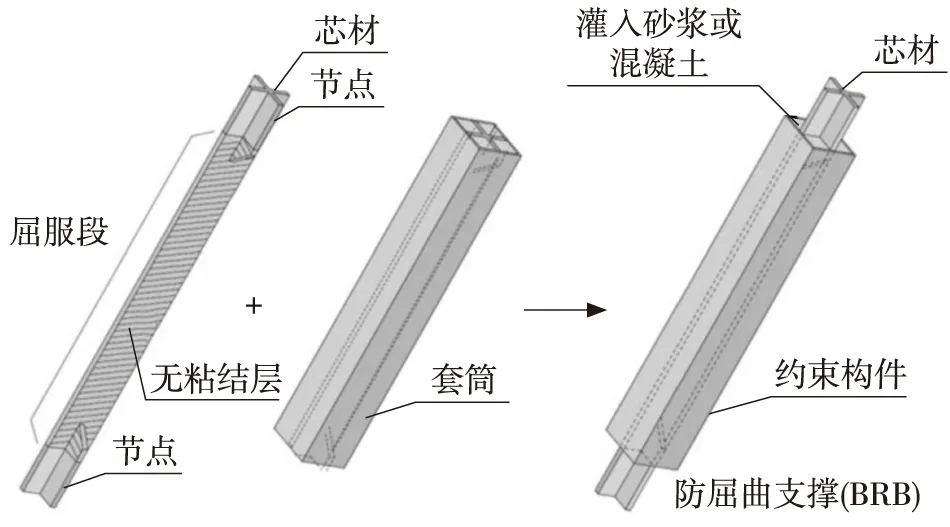
(a) 芯材 (b) 套筒 (c) 约束构件

2 屈曲约束支撑力学模型

BRB力学模型为双折线弹塑性模型[12]，其力位移曲线如图2所示。坐标原点(0，0)与曲线峰值点(D，Fmax)的连线斜率称之为有效刚度Keff，其计算公式为：

(1)

式中：Keff为BRB的有效刚度；Kd为BRB的屈后刚度；Qd为BRB的特征强度；D为BRB的最大位移；Dy为BRB的屈服位移。

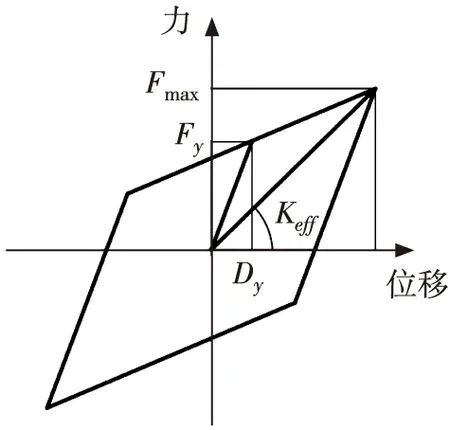
图2 BRB力位移曲线

从图2中得出，Dy为BRB进入屈服阶段时的位移，即屈服位移，其计算公式为：

(2)

每一个周期的BRB耗能面积Wd为：

Wd=4Qd(D-Dy)

(3)

BRB的有效阻尼比βeff为：

(4)

3 工程概况

主桥为预应力混凝土连续刚构，跨径布置为(73+130+73)m，由2个130 m T梁组成对称结构，主桥总长为276 m，如图3所示。箱梁顶宽16.5 m，底宽8.5 m，箱梁为单箱单室断面。主墩采用钢筋混凝土双薄壁空心墩，单肢平面尺寸为8.5 m×2.5 m，双肢壁面外到外距离11 m，承台厚度5 m，下设9根直径为2 m的钻孔灌注桩基基础。7#过渡墩采用钢筋混凝土薄壁等截面空心墩，10#过渡墩采用钢筋混凝土薄壁变截面空心墩，平面尺寸为8 m×2.6 m，承台厚3.5 m，采用6根直径2 m钻孔灌注桩基基础。主桥下部桩基按嵌岩桩设计，要求桩底嵌入风化岩层不小于8 m。

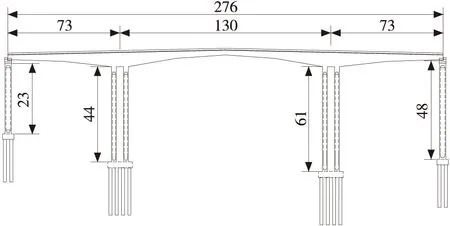
单位：m

4 有限元模型

采用有限元软件Midas Civil建立全桥模型。模型均采用梁单元模拟，模型中节点总数为176个，梁单元总数为166个。二期荷载和上部结构自重均转化为质量作用于下部结构。边跨端部采用一般支承，即不考虑边墩支座的摩擦力影响。为了方便计算，桥墩墩底采用固结方式，没有考虑桩土相互作用效应。在全局坐标系中，桥墩顺桥向从左至右分别为1#墩和2#墩，全桥模型如图4所示。

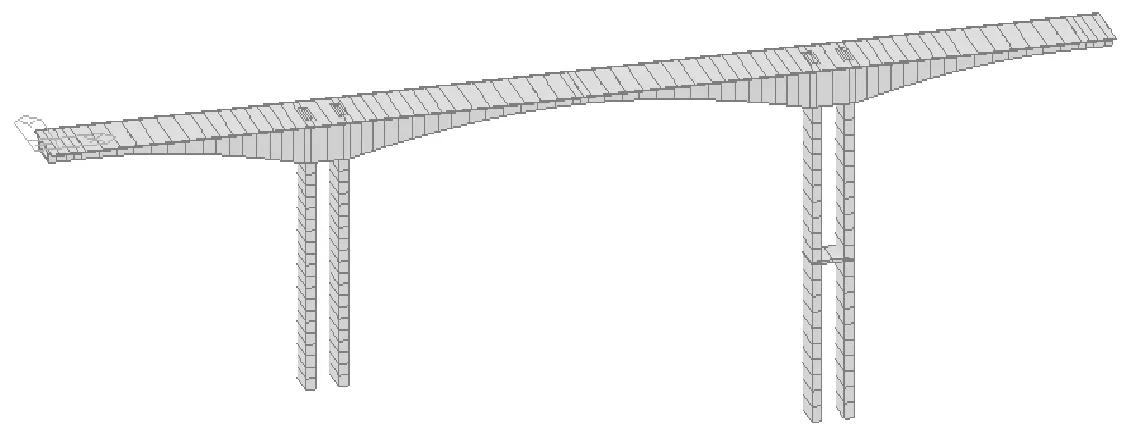
图4 连续刚构桥有限元模型

由于模型为钢筋混凝土结构，因此结构阻尼比取0.05。地震模拟采用3条天然波进行，取计算结果的最大值[13-15]。

5 地震动输入

本文采用3组天然强震地震波记录，分别为：1) 1940，El Centro Site，180 Deg，加速度峰值0.21g，持续时间为53.46 s，如图5(a)所示；2) 1989,Loma Prieta，Oakland Outer Wharf，0 Deg，加速度峰值0.20g，持续时间为39.98 s，如图5(b)所示；3) T1-I-1(1978，MIYAGI-Coast，LG)，加速度峰值0.32g，持续时间为30.00 s，如图5(c)所示。

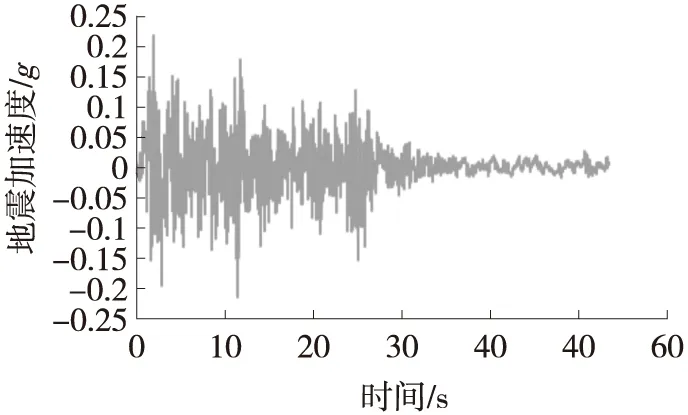
(a) EL Centro波加速度时程曲线

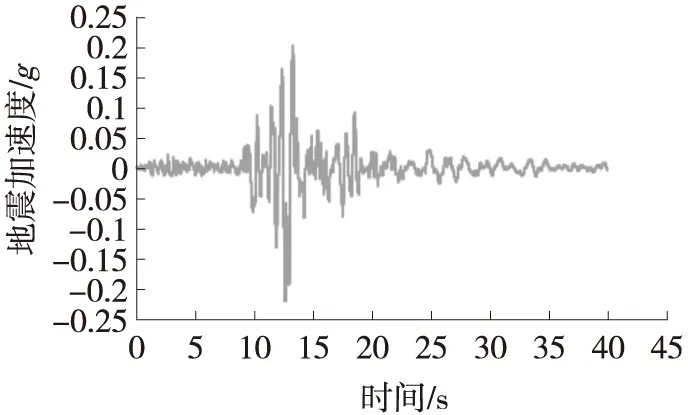
(b) Oakland Outer Wharf波加速度时程曲线

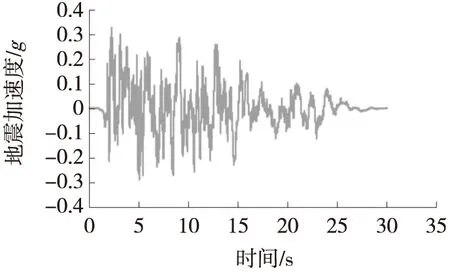
(c) MIYAGI-Coast波加速度时程曲线

6 屈曲约束支撑减震规律研究

6.1 不同支撑位置减震效应研究

连续刚构桥的桥墩较高，BRB布置在桥墩不同的竖向位置可能会有不同的减震效果。为了分析屈曲约束支撑在桥墩竖向上不同位置时的减震效果，分别模拟分析了BRB布置在墩上部、中部、下部时桥梁的地震响应，结果见表1。屈曲约束支撑布置方式为交叉支撑，屈服强度为4 300 kN，支撑角度为45°，分别选择1#墩墩顶位移、墩底剪力和墩底弯矩作为地震响应分析。

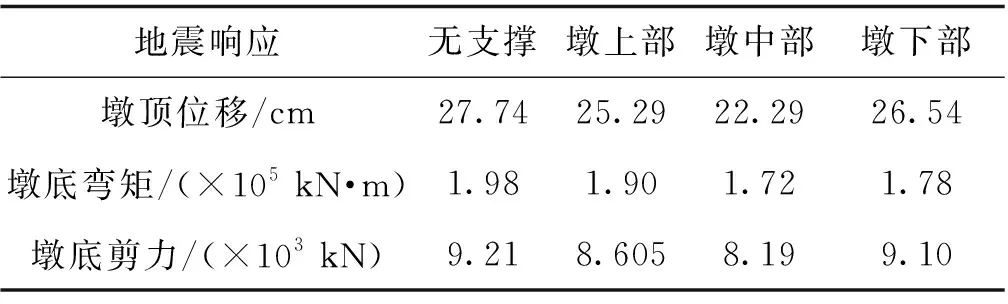
表1 不同支撑位置桥墩的地震响应

从表1可知，屈曲约束支撑布置在桥墩上部和桥墩下部的减震效果基本一致，而将支撑布置在桥墩中部的减震效果明显好于其他位置，墩顶位移减小显著。因此，将屈曲约束支撑布置在桥墩中部时更有利于减小下部结构的地震响应，具有更好的减震耗能效果。

6.2 不同支撑角度下的地震响应分析

为分析BRB采用不同支撑角度时的减震效果，在桥墩中部设置屈服强度为4 300 kN的BRB，研究支撑角度为0°、30°、45°、60°时BRB的减震效果。选择1#墩左肢墩墩顶位移、墩底剪力、墩底弯矩为对象进行地震响应分析，并从中选择最佳的支撑角度，结果如图6所示。

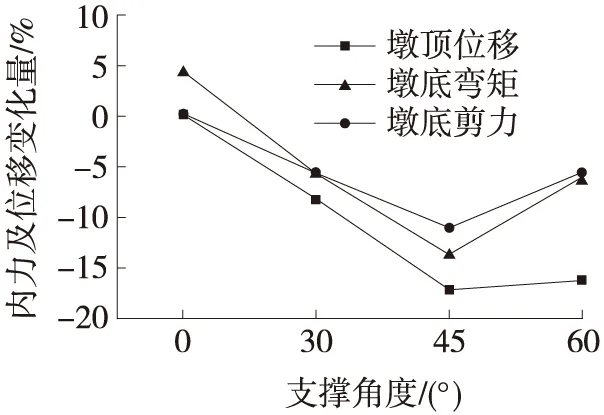
图6 BRB不同支撑角度对桥墩地震响应的影响

当BRB的支撑角度为0°时，即将BRB水平放置时，桥墩的地震响应不仅没有减小，反而还有少量增加。分析原因是水平布置BRB增加了桥梁结构的水平刚度，致使地震内力增加。除水平布置BRB外，其他角度布置BRB都有利于减小桥墩的地震响应。在支撑角度为45°时，桥墩的地震响应减小最为显著。因此，屈曲约束支撑的角度设置为45°时，耗能效果最佳。

6.3 不同支撑数量下的地震响应分析

为分析屈曲约束支撑装置不同支撑数量对减震效果的影响，针对以下5种工况进行地震响应分析：1) 墩中部设置1个支撑；2) 墩的中部和下部各设置1个支撑；3) 墩的中部和上部各设置1个支撑；4) 墩的上部和下部各设置1个支撑；5) 墩的上中下部各设置1个支撑等。响应结果见表2。分析模型中的BRB为交叉支撑，屈服强度为4 300 kN，支撑角度为45°。

表2 不同支撑数量下关键部位内力响应

墩顶位移在5种工况支撑数量下，减小的百分比分别为-17%、-25%、-18%、-10%、-26%。从表2可知，在墩的上中下位置各设置1个BRB时，墩顶位移减小的百分比最大，达到-26%；墩底弯矩在5种工况支撑数量下，减小的百分比分别为-13%、-18%、-17%、-9%、-24%，在墩上中下位置各设置1个BRB时墩底弯矩减震效果最好，达到-24%；墩底剪力在5种工况支撑数量下，减小的百分比分别为-11%、-4%、-33%、-19%、-28%。BRB支撑的屈服力、截面积、支撑形式、支撑角度不变的前提条件下，不同支撑数量都能取得良好的减震效果，仅在墩中部设置1个BRB，虽减震效果不是最好的工况，但与最好减震效果的工况相比较，两者的减震效果差别不大。综合经济和效果，建议在桥墩中部设置1个BRB是最经济合理的，同时也有良好的减震效果。

6.4 BRB屈服力对桥梁减震效果的影响

为分析BRB不同屈服力的减震效果，在桥墩的中部设置一个BRB，支撑角度为45°。通过计算，分析屈服力从300 kN增加到10 000 kN时桥梁结构的减震效果。选择1#墩左肢墩墩顶位移、墩底剪力、墩顶纵向位移、墩底弯矩、支撑部位桥墩的剪力和弯矩为对象进行地震响应分析，并从中选择最佳的屈服力，结果如图7、图8所示。

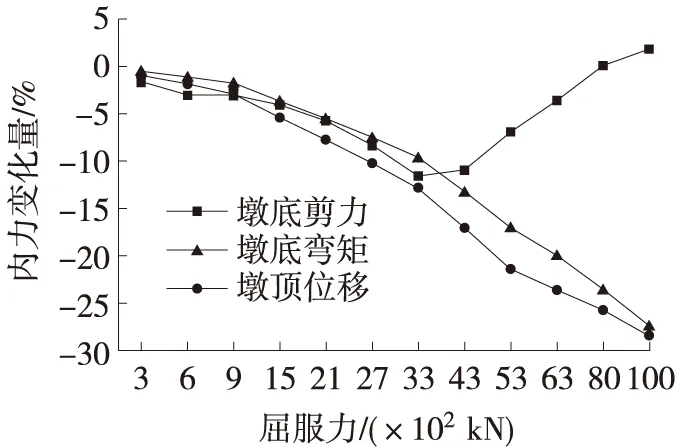
图7 屈服力和桥墩地震响应的关系曲线

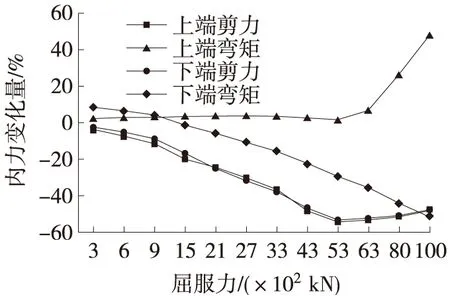
图8 支撑的端部剪力弯矩变化曲线

从图7、图8可知，随着BRB屈服力由300 kN增加到10 000 kN，1#墩墩顶位移不断减小，其中位移减小的范围从-1%到-28%；弯矩减小范围从 -1% 到-27%。1#墩左肢墩墩底剪力在BRB屈服力为300 kN到3 300 kN之间，墩底剪力不断减小，减小范围从-2%到-12%。当BRB屈服力从3 300 kN到10 000 kN之间时，墩底剪力呈递增趋势，递增范围从-12%到2%。以上变化表明在结构控制部位增设屈曲约束支撑装置后，其内力以及纵向位移响应总体减小，进一步说明BRB装置具有减小地震作用的效果。不同的屈服力对于减震效果的影响不同，墩顶位移和墩底弯矩呈现不断减小的趋势，但是墩底剪力在一定范围内增加了结构的地震剪力需求，对结构产生了不利影响。

6.5 不同布置形式减震效果研究

为研究支撑的不同布置形式对桥梁地震响应的影响，分别分析无支撑、桥墩中部设置斜向支撑、交叉支撑和人字形支撑等4种工况。其中，斜向支撑和人字形支撑方式如图9所示,不同支撑方式下的响应结果见表3。分析中各种支撑的屈服力选用 4 300 kN，支撑角度为45°，分别选择1#墩墩顶位移、墩底剪力和墩底弯矩作为地震响应分析。

(a) 斜撑方式

(b) 人字形支撑方式

由表3可知，3种支撑方式都有利于墩顶位移的减小，交叉支撑较斜撑和人字形支撑墩顶位移减小得更加明显；单根斜撑方式不仅没有减小墩底弯矩，相反还增加了墩底的弯矩，交叉支撑和人字形支撑2种支撑方式对墩底弯矩影响不大，但两者较未设BRB时，墩底弯矩减小显著，且交叉支撑稍优。单根斜撑增大了墩底剪力，交叉支撑和人字形支撑较未设支撑时都减小了墩底剪力，且交叉支撑减小更显著。

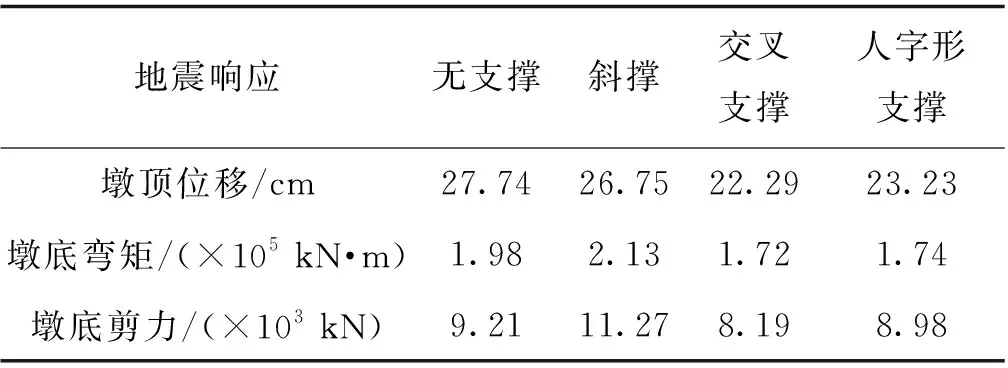
表3 不同支撑方式下结构地震响应

综上分析，在屈曲约束支撑的屈服力、支撑角度、支撑位置、支撑数量不变的前提下，采用交叉支撑更有利于减小结构的地震响应，具有更好的耗能效果。

7 结论

本文将屈曲约束支撑应用到高墩连续刚构桥，在双薄壁墩上安装BRB装置，通过数值模拟分析，得到如下结论：

1) 在双薄壁墩的2个肢墩之间安装BRB后能够有效减轻上部结构位移、桥墩墩底弯矩和剪力。

2) 在桥墩中部安装BRB的减震效果好于其他位置，其减震效率最高。

3) 采用交叉支撑更有利于减小强震作用下结构的地震响应，具有更好的耗能效果。

4) BRB的支撑角度设置为45°时更有利于系统的减震效果，能够具有最佳的耗能能力。

5) BRB的屈服力优化很重要，其大小直接影响桥墩的地震剪力需求。