既有桥梁抗震加固设防标准研究

唐光武，刘 亮，谢皓宇，刘 鑫

(1.招商局重庆交通科研设计院有限公司，重庆 400067； 2.桥梁工程结构动力学国家重点实验室，重庆 400067；3.中国市政工程西南设计研究总院有限公司，成都 610036； 4.中铁二院工程集团有限责任公司，成都 610031)

几次大地震一再显示了桥梁工程破坏的严重后果，也一再显示了桥梁工程抗震研究的重要性[1-2]。近几次大地震中，一些早期经过抗震设计的桥梁，在中等强度的地震作用下即遭到严重破坏，反映出以往的桥梁抗震设计规范存在着一定的缺陷[3]，各国相关工程师及学者对现行的抗震设计规范进行反思和修订，对结构的抗震设防标准与抗震设计原则也提出了一系列新观点[4-6]。

既有公路及城市桥梁在抗震性能加固设计时，首要问题是确定既有桥梁的抗震设防标准。由于既有桥梁一般都已服役一定年限，预期使用年限低于新建桥梁，从经济性考虑，其抗震加固设防标准也宜低于新建桥梁。

新建桥梁设防标准用地震动重现期或设计基准期内的超越概率来表达，抗震设计规范中一般用重要性系数和设计地震动基本峰值加速度来综合表达。因此，根据既有公路及城市桥梁遭遇的地震风险水平和新建桥梁一致的原则，通过调整、确定可变作用的设计基准期，研究并确定既有公路和城市桥梁的抗震加固设防标准，以期为既有桥梁抗震加固设计提供可靠的指导和依据。

1 理论基础

1.1 地震动基本峰值加速度和地震烈度

地震动基本峰值加速度和地震烈度分别作为描述地面振动强度与地震强度的指标，地震工程研究人员运用模糊数学已对2个指标之间建立了如下关系[7]：

A=10(Ic×log 2-0.104 757 5)

(1)

式中：A为地震动峰值加速度，gal；Ic为抗震设防烈度。

由式(1)可推导出抗震重要性系数Ci与设防烈度的关系：

(2)

式中：I为基本地震烈度。

以公路及城市桥梁现行抗震规范[8-9]为新建桥梁设防标准，进而计算出对应公路和城市桥梁各设防标准的烈度值，见表1、表2。表1、表2中，部分设防烈度有2个数据是由于城市与公路桥梁抗震设计规范中对于不同的桥型对应了不同的抗震设防标准(抗震重要性系数)，2个数据中处于下方的数据指大桥、特大桥。

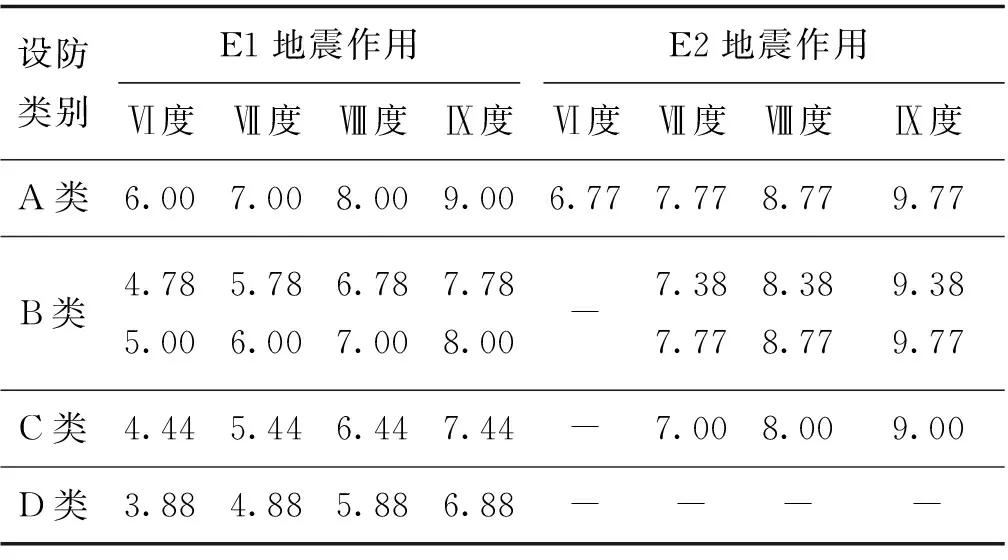
表1 公路桥梁各设防水准下抗震设防烈度

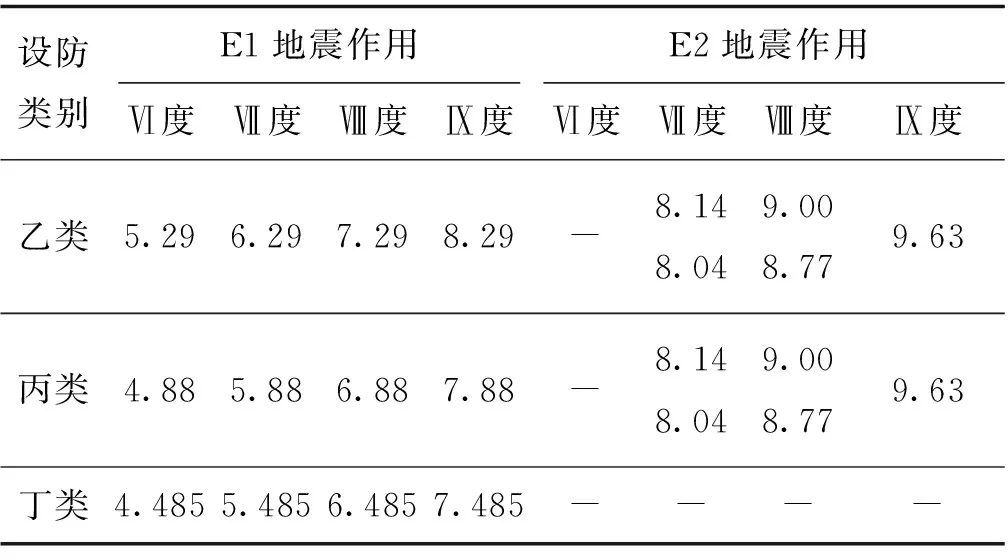
表2 城市桥梁各设防水准下抗震设防烈度

1.2 地震动参数的概率分布

地震的发生及传播在空间和时间上存在很大的随机性，因此，为确定设计基准期内场地遭遇不同强度地震作用的可能性及地震动参数的概率分布，首先需要分析地震危险性。在综合考虑场地周围可能存在产生影响的潜在震源的基础上，统计场地地震的历史最大烈度、相应重现周期、衰减规律及其它地震动参数等。采用数理分析的方法，在给定时间间隔内，计算具有给定发生概率的地震烈度或通过地震动参数来确定其概率分布。

在研究并确定地震动参数的概率分布时，目前国内外学者多采用泊松分布建立概率模型开展后续研究。Algermissen等[10]论证了地震动峰值加速度的概率分布符合极值Ⅱ型；Shibata和颜文晖等[11-12]论证了地震震级的概率分布符合极值Ⅲ型；鲍霭斌等[13]对我国65个城镇进行地震危险性分析，研究并证实了地震烈度的概率分布符合极值Ⅲ型，并用极值Ⅲ型拟合设计基准期50年地震烈度概率分布函数为[14-15]：

(3)

式中：F(Ic)为基准期内小于或等于Ic的概率；T为设计基准期；ω为地震烈度上限值，取12；Iξ为地震烈度众值，取基本烈度减1.55度；k为形状系数。从工程实用的角度，取50年基准期内超越概率为10%的地震烈度确定k值，见表3，并拟合出了确定k值的函数[14-15]：

(4)

对于随机变量Ic，概率分布函数F(Ic)和超越概率函数P(I≥Ic)存在如下关系:

(5)

式中：P(I≥Ic/T)为基准期T年内大于或等于烈度Ic的概率。

表3 对应地震基本烈度的形状系数

由式(3)可推导出基准期T年内发生大于或等于设防烈度Ic的地震年超越概率P(I≥Ic/T)：

(6)

年超越概率P(I≥Ic)与地震重现期RP的关系：

(7)

2 既有桥梁抗震设防标准确定

在确定既有桥梁抗震设防标准时，为方便计算，作如下假定[12]：

1) 既有桥梁的预期使用年限仅由桥龄与设计使用年限决定。

2) 新建桥梁设计使用年限统一取值100年。

我国公路及城市桥梁现行抗震设计规范，以设计基准期50年内超越概率10%的地震动参数为基础确定抗震设防标准，而新建桥梁设计基准期为100年。据此，首先应确定设计基准期100年内的超越概率(按年超越概率相当的原则)，再根据既有桥梁的预期使用年限，通过调整确定可变作用的设计基准期，按照既有桥梁设计基准期(T<100年)内超越概率水平和新建桥梁设计基准期(T=100年)内超越概率一致的原则来确定既有桥梁的抗震设防标准。

鉴于形状参数k的取值及现行抗震设计规范均按设计基准期50年内超越概率为10%确定，最后按年超越概率相当的原则，计算既有桥梁各预期使用年限的50年设计基准期内的超越概率来确定既有桥梁的抗震设防标准，并采用抗震重要性系数来表达。

具体步骤如下：

1) 根据新建桥梁的两水准(E1地震、E2地震)设防标准，按50年设计基准期计算设计地震动的超越概率以及相应的年超越概率和重现期。

2) 按照年超越概率相当(重现期相当)的原则，确定100年设计基准期内的超越概率P(I≥Ic/100)。

3) 按照既有桥梁T(T≤100)年设计基准期内超越概率水平和新建桥梁100年基准期内超越概率一致的原则，确定既有桥梁抗震设防标准，即T年设计基准期内年超越概率P(I≥Ic)。

4) 按照和既有桥梁年超越概率相当的原则，确定50年设计基准期内超越概率P(I≥Ic/50)，并计算形状系数k。

5) 计算对应既有桥梁两水准(E1地震、E2地震)抗震设防标准的抗震重要性系数或地震动参数。

由以上步骤求得预期使用年限t(t<100)年的重要性系数平均系数比和平均降低率，结果见表4，其中重要性系数的降低率见图1。本文按照抗震设计规范和抗震重要性系数平均降低率来确定既有桥梁设防标准。

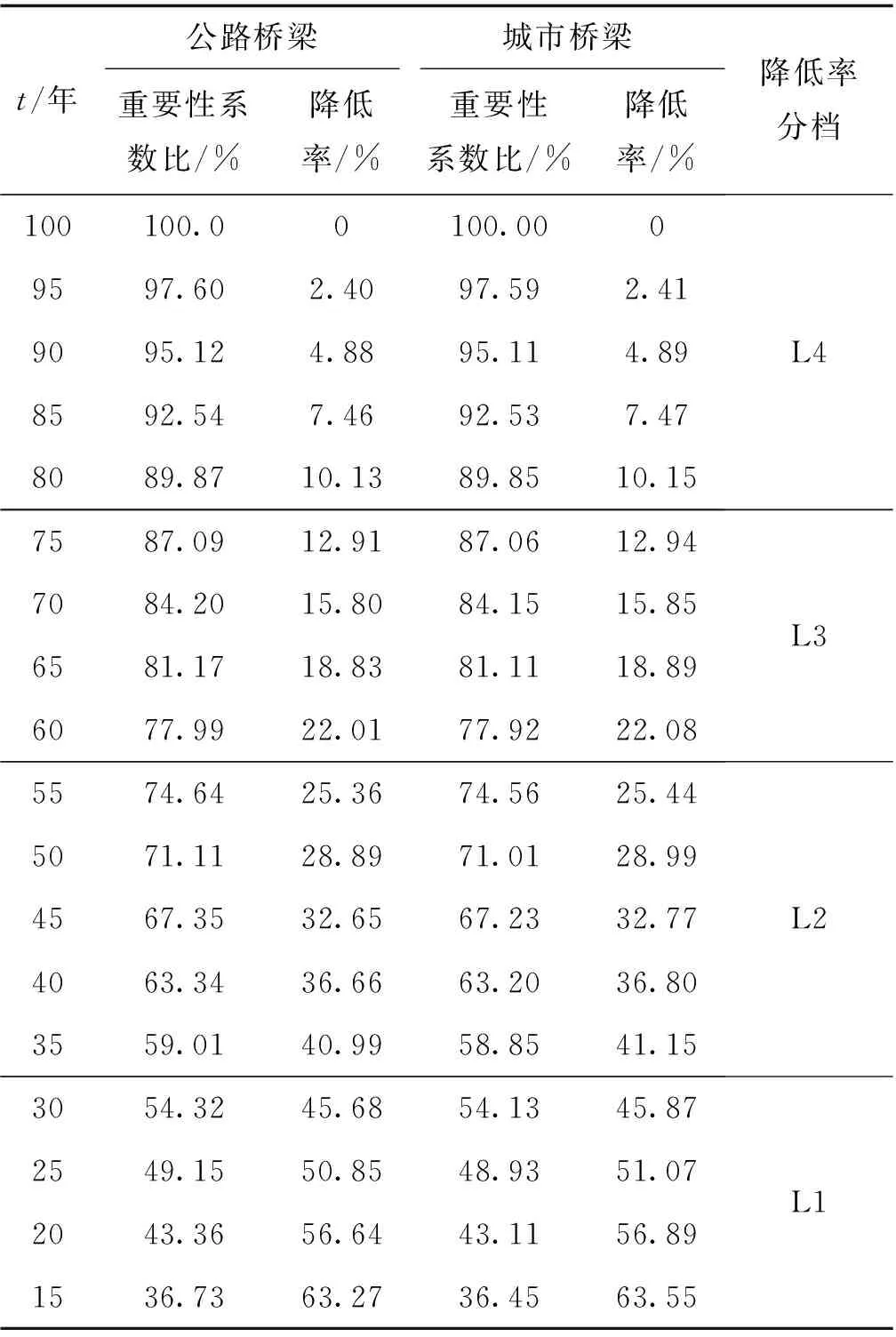
表4 重要性系数比和降低率

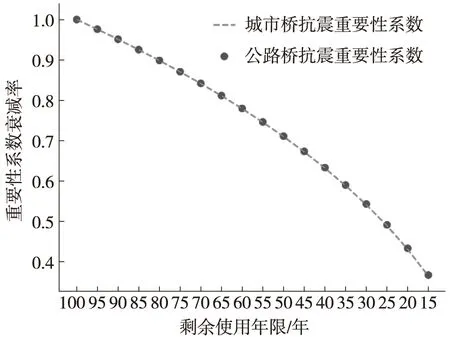
图1 公路及城市桥梁抗震系数折减

1977年，我国首部公路工程抗震设计规范颁布实施(其中包括公路桥梁抗震设计)，距今已有40多年。在此之前设计的公路及城市桥梁大多未进行抗震设计，或按照工程经验或参考相关技术资料设计，抗震性能可能存在不足。据此，既有桥梁抗震设防标准首先将60年作为既有桥梁设防标准的分水岭，再在60年前后进一步划分范围。

预期使用年限t≥60年的桥梁进行了专业的抗震设计，再按照10%的平均降低率划分较为安全经济；预期使用年限t<60年的桥梁未进行专业的抗震设计，其抗震性能可能存在明显的不足，再按照20%的平均降低率进行划分；从经济性考虑，t<15年的桥梁不再考虑抗震加固。

综上所述，既有桥梁的抗震加固设防标准按照5档进行划分，见表5；各档设防标准的抗震重要性系数见表6～表9。其中，根据剩余使用年限修正的公路桥梁抗震重要性系数见表6，根据剩余使用年限修正的城市桥梁地震调整系数见表7～表9。

表5 既有桥梁设防标准

由表6～表9可以看出，传统既有桥梁抗震性能评估中使用不考虑预期使用年限(即按新桥标准

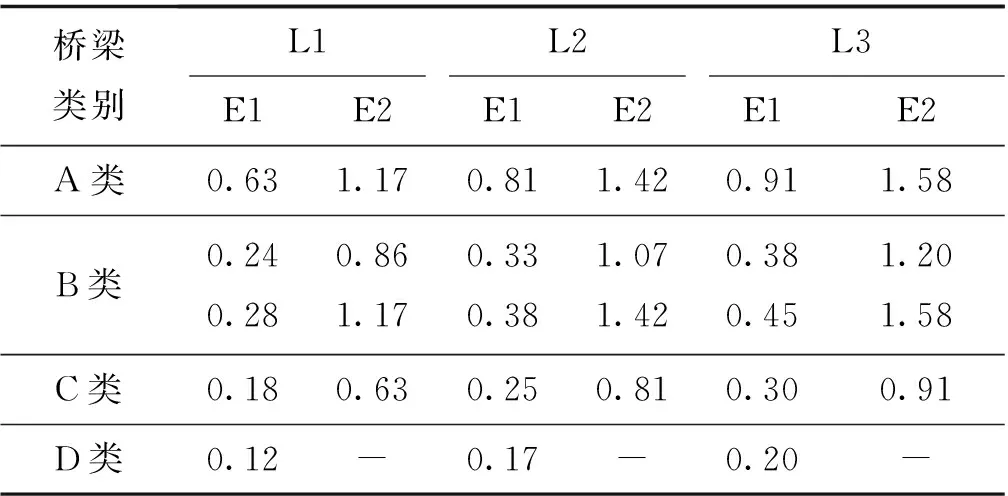
表6 公路桥梁抗震重要性系数

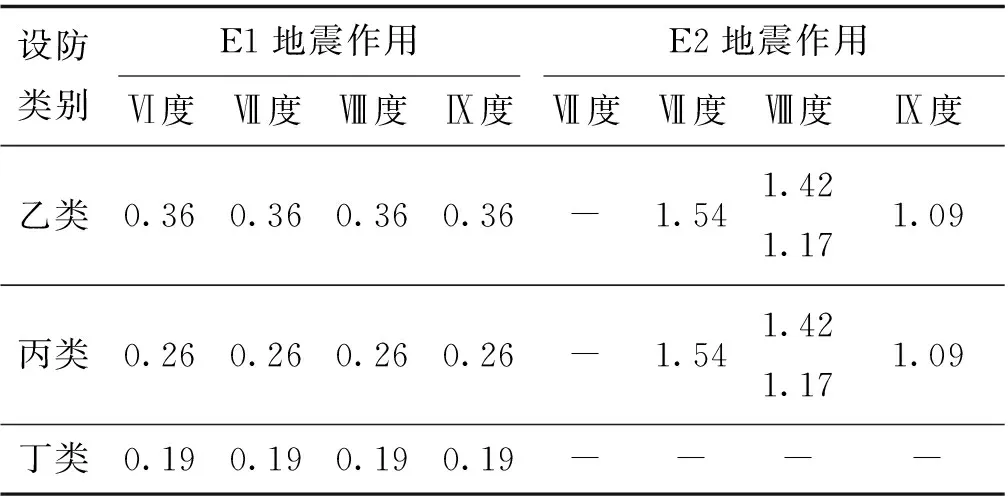
表7 L1城市桥梁地震调整系数

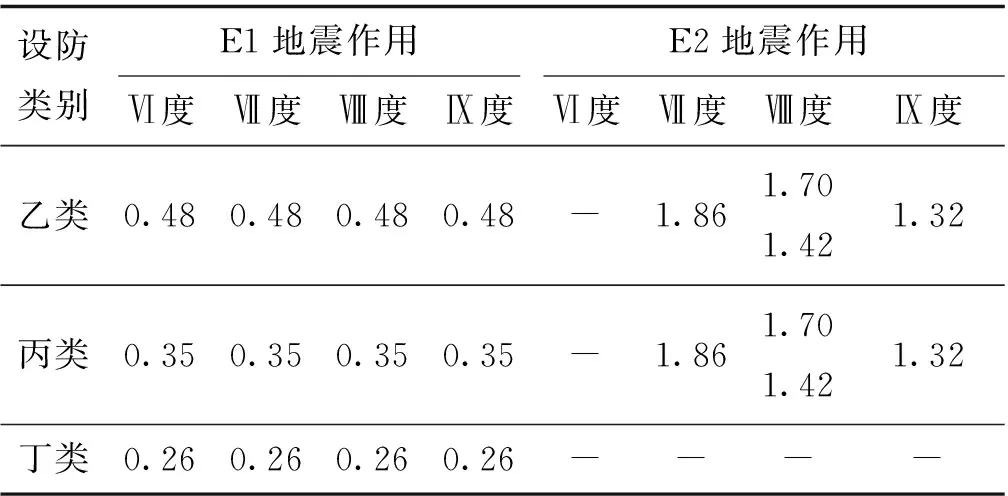
表8 L2城市桥梁地震调整系数

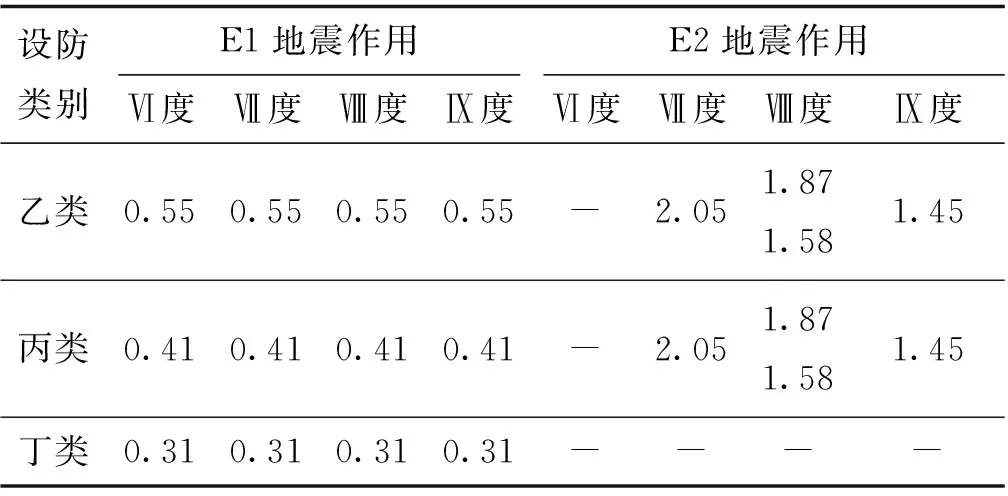
表9 L3城市桥梁地震调整系数

要求)的地震动强度不满足一致危险性原则，高于实际的抗震性能需求，而本研究所提出的调整过后的抗震重要性系数(城规中为地震调整系数)可为学者、工程师提供符合震后桥梁实况的合理依据。

3 结论

本文基于对既有桥梁抗震加固设防特点的把握，以现行规范抗震设防标准为基础，通过调整重要性系数来确定既有桥梁的抗震加固设防标准，得出如下结论：

1) 基于概率理论的公式推导可知，当桥梁剩余使用年限不断降低时，在一致危险性原则下，抗震重要性系数下降很快，在做既有桥梁抗震加固时，须将其考虑在内，确定抗震设防标准。

2) 按一致危险性原则，计算了不同设计基准期桥梁抗震重要性系数，并将公路、城市桥梁抗震设防标准按预期使用年限划分成5档，且给出了各档抗震重要性系数，分别是：预期使用年限t≤15年，无需设防；15