顶管渐变置换法控制软土路基不均匀沉降效果研究

柴贺军，涂义亮，徐建强，李海平

(1.招商局重庆交通科研设计院有限公司，重庆 400067； 2.山区道路工程与防灾减灾技术国家地方联合工程实验室，重庆 400067)

在我国的东部沿海地区，桥头跳车是常见病害之一。据有关调查，路桥过渡段的维修费用占总费用的70%以上[1]。

桥头跳车现象主要是因外部车辆荷载长期、反复的作用，使得桥台与道路间产生过大的差异沉降[2]，常在软土地区公路中出现。目前，对于桥头跳车处治方法，主要有桥头搭板法、土工格栅法、加铺法和轻质材料置换法等[3-5]。加铺法和桥头搭板法只能起到一定的减缓作用，后续可能耗费更多的财力、物力去维护。土工格栅法及轻质材料置换法需要开挖路面，这对运营期高速公路不太适用，且轻质材料置换法适合软土较薄路基，有较大的局限性。针对这些问题，提出顶管渐变置换法，该法在不干扰路面正常交通的情况下，采用管道对路堤土进行置换，使得路堤自重降低，实现处治路桥过渡段不均匀沉降的目的。Yang S等[6]通过太原火车站隧道穿越工程，对密排顶管进行研究，得到管道过于密集，管道之间的土体会被紧密压缩，形成管-土拱效应；Yang X等[7]对膨胀土顶管施工中的水溶性泥浆进行改进，使得顶进力显著减小，并提出一种较为简便的顶管顶力计算方法；江正潭[8]在后屠中桥桥头跳车处治中对顶管减载处理方案的施工方案、工艺、控制标准等进行了介绍；包龙生等[9]采用预埋管涵方式对桥头跳车进行处治。但上述研究都未研究间距对处治效果的影响，忽略了沿路线方向控制沉降平缓过渡的重要性。因此，需要对顶管渐变置换法的参数设计和实施效果进行研究。

本文依托直上河桥路段工程，提出顶管渐变置换非开挖处治方法；通过三维数值模拟首先分析10 m范围内不同处治间距对沉降控制的影响规律，为渐变间距提供设计参考；然后对提出的渐变设计方案进行了验证，研究成果可为今后运营期的公路桥头跳车问题处治提供借鉴。

1 工程概况及数值模型的建立

1.1 工程概况

直上河桥宽度约为19.3 m，地层分布为黏土、淤泥Ⅰ、淤泥Ⅱ、淤泥质黏土Ⅰ及淤泥质黏土Ⅱ。该桥运营以来，一直以路面加铺的方式处治桥头跳车现象，历次加铺下来，极大增加了路堤的自重，加剧了不均匀沉降，如图1所示。

1.2 原始路基数值模型的建立

考虑到路基的对称性，取一半对其进行建模分析，原始路基模型如图2所示，并在路面中心、路肩及路堤坡脚各设置1个位移监测点。

软土地层采用修正剑桥模型模拟，因修正剑桥[10]适合正常固结土和超弱固结土的弹塑性模型，适用于模拟固结压力对材料特性有重要影响的软黏土，路堤填土采用M-C模型模拟，其粘聚力为25.6 kPa，内摩擦角29.8°，土层参数如表1所示。固结沉降分为主固结和次固结，主固结为粘弹性沉降，采用FLAC3D流固耦合分析；次固结为粘弹性和粘塑性沉降，采用Burgers模型模拟，固结计算参数如表2所示。交通荷载取14 kN/m2的均布应力施加于路面上。

图1 桥头跳车

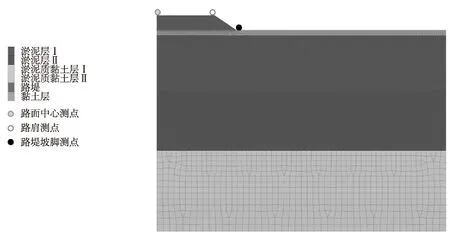
图2 原始路基模型

1.3 数值模型验证

对数值模型计算19年，即2000—2019年，其数值模拟结果曲线与现场监测数据如图3所示。从图3中可以看出，数值模拟曲线与实际现场监测数据拟合较好，验证了数值模型的可行性。继续对模型进行运算至2039年，从图3中还可以看出，20年后，路面最大沉降量达到0.539 m，如果不进行处治将会产生严重的桥头跳车问题。

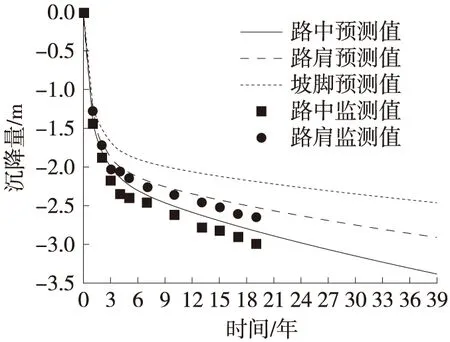
图3 2000—2039年不作处治预测沉降曲线

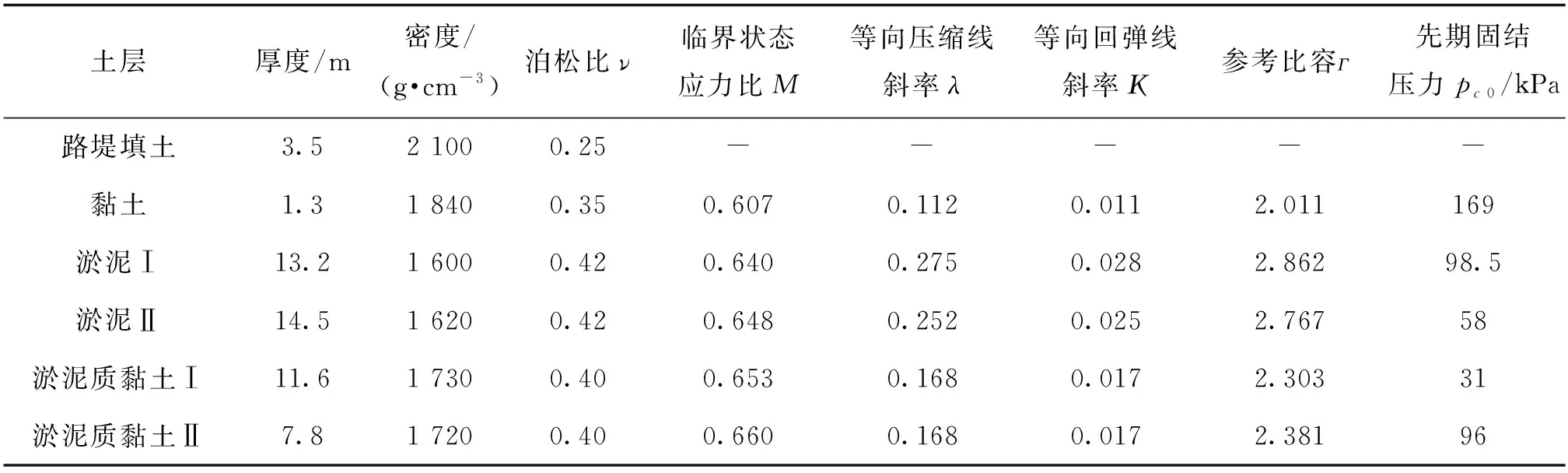
表1 土层参数

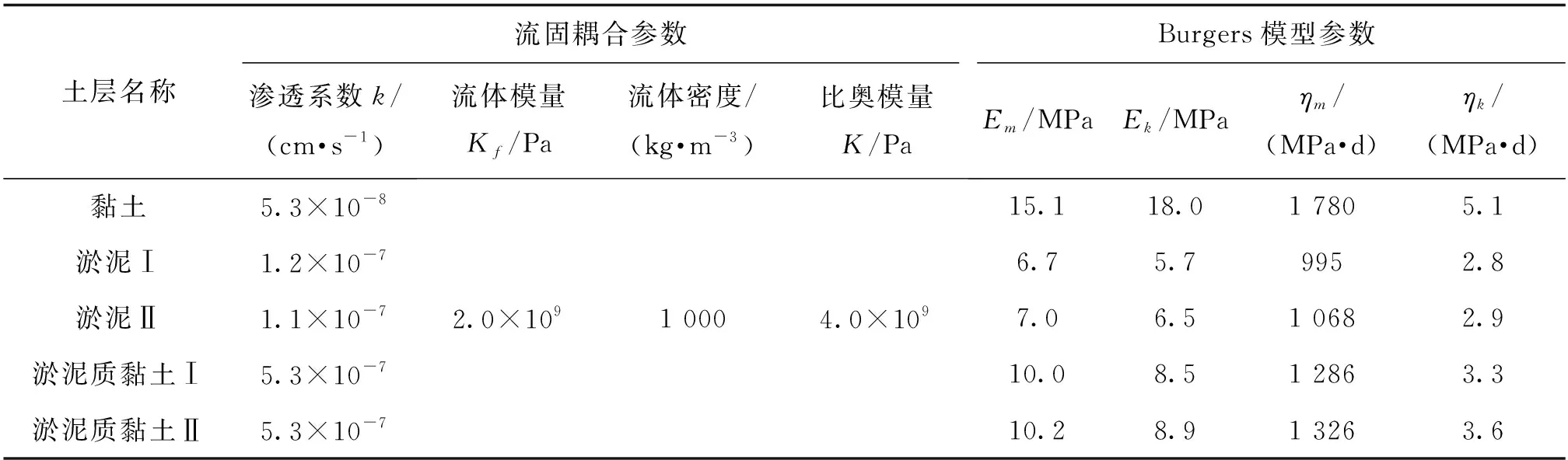
表2 直上河桥桥段路基固结沉降参数

2 顶管置换间距的影响规律

为处治直上河桥段的差异沉降，提出顶管渐变置换方法。通过沿道路方向改变顶管间距使得总体沉降处于可控范围。因此，有必要分析顶管间距对沉降控制的影响。

2.1 顶管置换处治数值模型建立

建立不同间距的顶管数值模型，模型长58 m，高55.5 m，沿道路方向厚度为10 m，如图4所示。顶管尺寸参照非开挖处治协会有关规范[11]取直径为0.6 m，厚度为10 mm，采用壳单元模拟顶管，壳单元参数取值为：弹性模量E=206 GPa，泊松比ν=0.3。

2.2 数值模拟结果分析

先模拟未处治时的路基状态，对模型运算19年，即2000—2019年，再将壳单元施加在模型中，并将其内部土体删除，对模型继续运算20年，得到监测点沉降与时间关系曲线，如图5所示。

从图5中可得，在2019—2039年间，路桥过渡段经顶管置换法处治后沉降量明显减小，且随着顶管间距的减小，沉降控制效果呈上升趋势。在同一时期，间距为1.06 m时，处治效果最好，其最终沉降量减少了0.172 m，位移云图如图6所示。从图6中可以看出，经处治后，沉降主要发生在路堤处，且越接近路面中心，沉降量越大，是由车辆荷载作用引起的，距离荷载作用位置越近，影响越大。

不同顶管间距对沉降处治的影响如图7、图8所示。 从图7、图8可以得出，随着间距的减小，路堤减载越大，路基沉降量逐渐减小，沉降量变化百分比也逐渐增大，沉降控制效果逐渐增强。间距为1.06 m时，沉降量变化最为明显，最大沉降减少量百分比达到29.30%，且在顶管施工过程中,管道周围地层就会发生形变而产生应力释放, 这是管道周边应力向四围传递的结果，即土拱效应[12]，在一定程度上降低了因土层损失、收敛位移所造成的地表沉降。综合考虑路桥过渡段不同区域对沉降要求，对顶管间距进行渐变设计，使得路桥过渡段沉降呈平缓过渡。

(a) 顶管间距1.06 m

(b) 顶管间距1.60 m

(c) 顶管间距2.39 m

(d) 顶管间距3.41 m

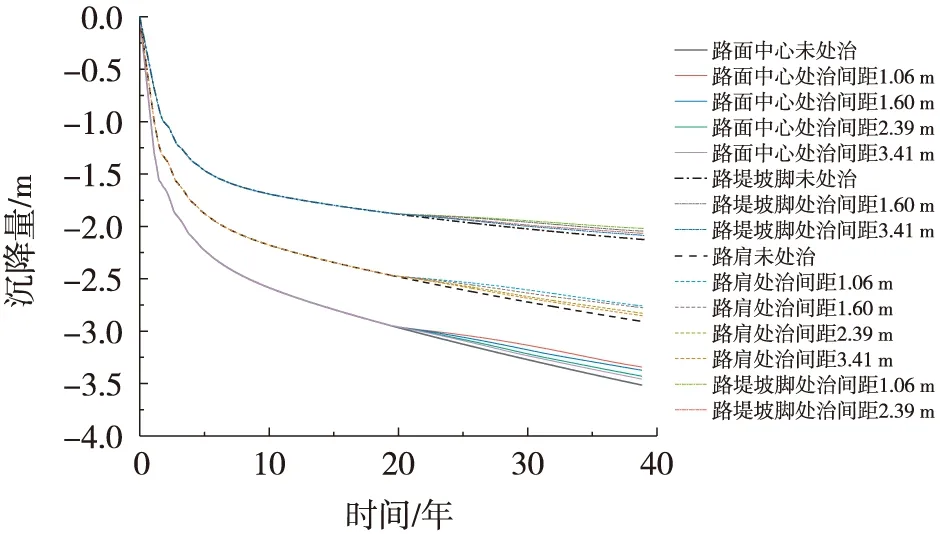
图5 2000—2039年各区域沉降曲线

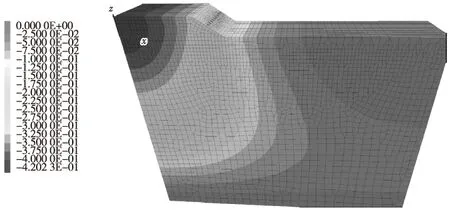
图6 处治间距为1.06 m的沉降位移云图

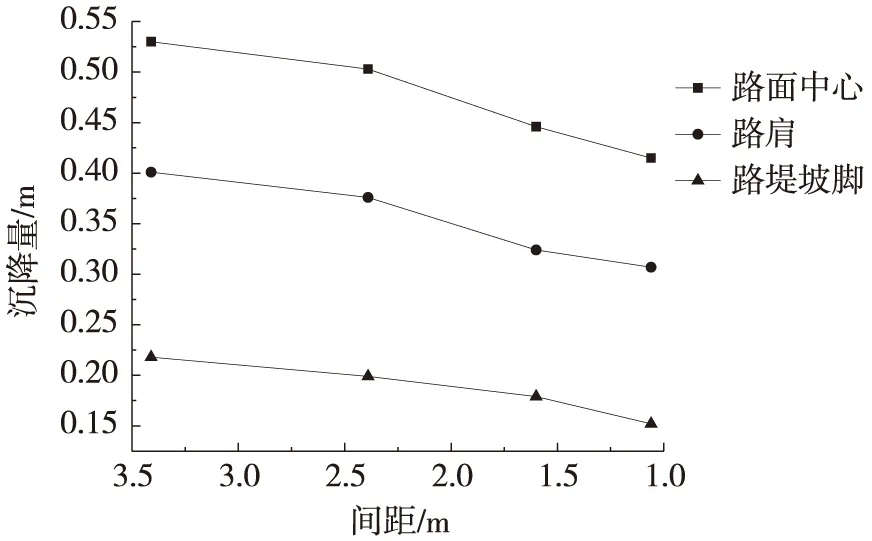
图7 不同间距处治下20年后的沉降量

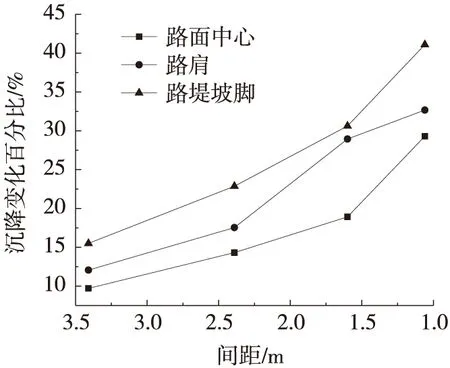
图8 不同间距处治下20年后的沉降量变化百分比

3 顶管渐变置换法处治效果分析

3.1 处治方案参数确定

根据上述结果，对路桥过渡段进行顶管渐变置换处治。将路桥过渡段分为A、B、C、D四个分区，各分区范围分别为11.32 m、10.97 m、7 m和10.28 m，各分区顶管间距分别为1.06 m、1.60 m、2.39 m、3.41 m，顶管直径均为0.6 m，如图9所示。

3.2 不处治下的三维数值模型

建立148 m×60 m×48.4 m验证数值模型，路面宽28 m，路堤坡率为1∶1.5，如图10所示。在路桥连接处设置2块长8 m、厚0.6 m的搭板。

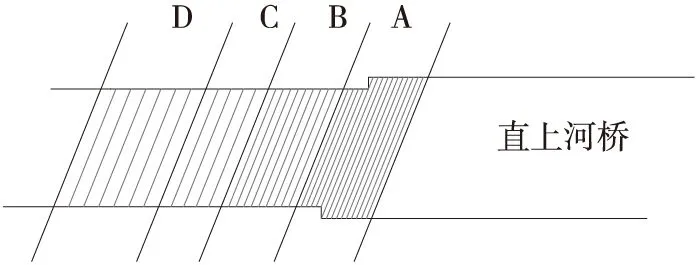
图9 各分区顶管布置

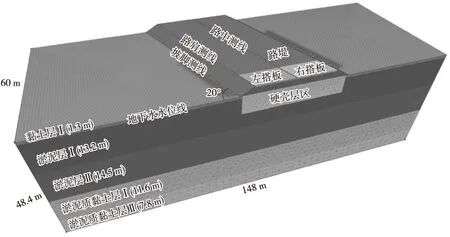
图10 验证计算模型

3.3 不处治下的沉降量

对不处治模型进行运算至2039年，得到模拟沉降云图，如图11所示。由图11可得到在20年后，路面、路肩及路堤坡脚持续沉降至3.385 m、2.913 m、2.459 m，沉降量变化量分别为0.555 m、0.389 m、0.269 m。如不对其进行处治，将来会产生严重的桥头跳车问题。

图11 2000—2039年不作处治下的沉降云图

3.4 顶管置换渐变处治数值模型

采用FLAC3D建立顶管置换渐变处治模型，如图12所示。

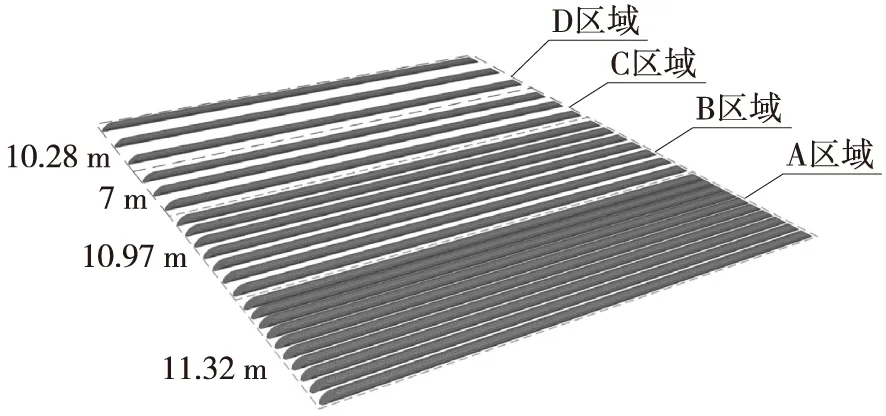
图12 顶管渐变置换处治数值模型

3.5 顶管置换渐变处治效果分析

先模拟不处治状态下的路基沉降至2019年，然后将壳单元施加在模型中，模拟处治后20年内的路桥过渡段沉降情况。

1) 不同处治区域沉降控制效果

模拟运算得到处治20年后各分域的最终沉降，如表3所示。从表3可得，在2019年开始顶管置换处治后，各区域沉降量明显减小，其中A处治区域控制沉降效果最好，相对沉降量降低百分比达到27.76，B、C、D处治区域沉降控制效果随着顶管间距增大逐渐减弱。处治20年后顶管的沉降位移云图如图13所示。从图13可以看出，沉降主要发生在路面中心位置，顶管间距越小，沉降量越小，说明顶管越密集，路基减载越大，同时，顶管本身具有一定的强度，下穿路堤后，形成类似梁结构，很好地承担了上部荷载，变相提高了路基的刚度，进而有效控制了沉降。

2) 变刚度处治区变形协调特征

处治后路面中心沉降与桥头距离的关系曲线如图14所示，路面沉降云图如图15所示。从图14中可以看出，路面中心沉降值随着时间及桥头距离的增大而增大，路堤沉降沿线路方向呈现较平缓的渐变效果，验证了顶管渐变置换处治方案能有效处治桥头跳车问题。

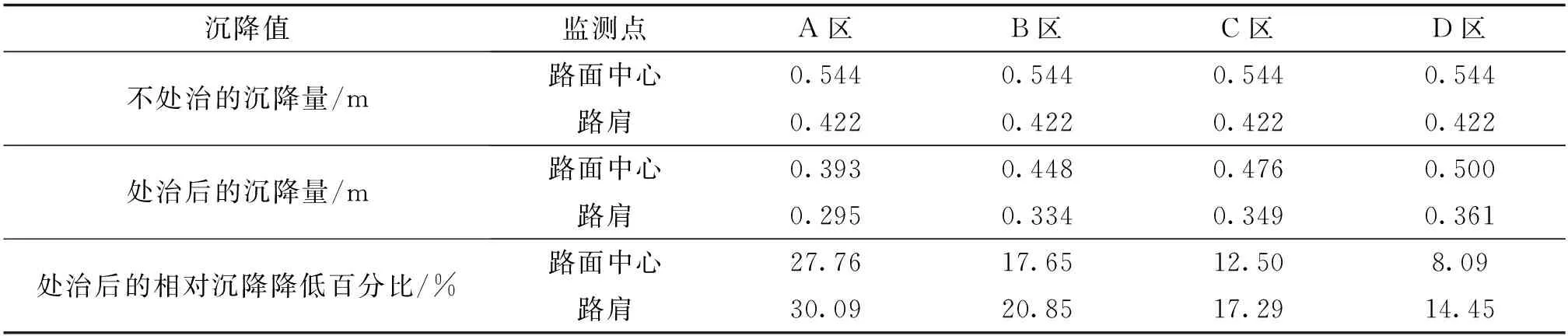
表3 处治20年后不同区域最终沉降对比

图13 处治20年后顶管沉降位移云图

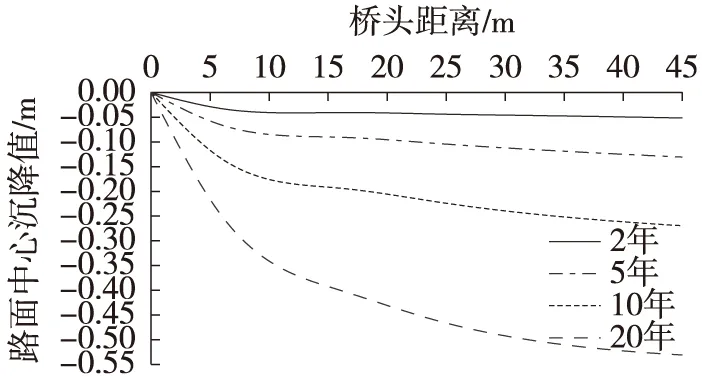
图14 处治后路面中心沿线路方向沉降值

图15 2039年路面沉降云图

4 结论

1) 顶管渐变置换法随着顶管间距的减小，处治效果逐渐增强，当间距为1.06 m时，沉降控制效果最好，且在顶管施工过程中，存在土拱效应，在一定程度上延缓和降低了地表沉降。

2) 顶管渐变置换法在处治桥头跳车问题上，一方面，顶管置换出来土体在很大程度上减轻了路堤自重，且随着间距的减小，路堤自重荷载降低越大，沉降量也随之减小；另一方面，顶管下穿路堤形成类似梁结构，很好地承担了上部路堤自重和交通荷载，变相提高了路基的刚度。

3) 通过对桥头跳车段进行分区渐变处治，顶管间距沿线路方向逐渐增大，路面沉降也随之呈现平缓的渐变效果，提高了行车安全性和舒适性，桥头跳车问题得到较好缓解。