狙击步枪瞄准系统自动校正方法研究

鄢砚军,余 雷,彭志召,施光礼

(1.中国人民解放军91892部队,海南 三亚 572099;2.陆军装甲兵学院,北京 100072)

科学技术的发展推动狙击步枪持续更新换代,每一次更新换代,狙击步枪的性能指标如射击精度、有效射程、可靠性和杀伤力等都会得到一定程度提高。实战中,狙击步枪的弹道轨迹[1]受气温、气压、风向、风速、空气湿度、射角、弹丸速度和重力等多方面因素的影响,培养一名优秀的狙击手需要一个系统的训练过程,不仅训练周期长,还需要狙击手有一定的天赋。狙击手对远距离目标射击需要借助瞄准器材[2-3],射击前需要进行校准[4],射击过程中射手需要充分考虑外界因素和目标距离对弹道的影响,结合自身经验进行修正,采取调整瞄准镜上下、左右旋钮或采用偏差瞄准的方式实现精准射击。

当前世界上现役的几款狙击步枪,如中国10式狙击步枪、美国巴雷特M82、俄罗斯OSV96、奥地利斯太尔SSG69、英国北极战马格努姆等均需要通过人工对瞄准点进行修正,当外界条件因素复杂时,狙击手可能出现对环境因素判断不准、弹道计算错误、修正错误或多次修正后找不到初始射击校准点的情况。为此,本文提出一种狙击步枪瞄准点自动校正的方法,该方法通过微型辅助设备测量影响狙击步枪弹道外界因素的数据参数,通过弹道解算系统和自动校正系统自动计算出瞄准点的位置,使用该系统减少了射手计算弹道时的误差,有效提高了狙击步枪射击的效率,提高了射击精度,增强了狙击步枪对恶劣环境的适应性。

1 总体技术方案及基本设置

1.1 系统组成及工作原理

狙击步枪瞄准点自动校正系统主要由探测系统、弹道解算系统和自动校正系统组成。探测系统主要由温度探测器、风速风向测量仪、激光测距机、角度仪、海拔高度测量设备、重力加速度测量仪器等组成,用以探测各类影响狙击步枪弹道轨迹因素的数据。弹道解算系统将探测到的各种数据输入到控制中心进行计算,得出弹丸发射后的外弹道轨迹,得出相应的偏移量。校正系统[5]是在确定弹丸初始位置、射击距离和弹道偏移量的情况下,反向计算出狙击步枪应调整的射角,进一步计算出狙击步枪瞄准点在瞄准镜中的位置,将瞄准点以十字或者红点的形式投影到瞄准镜[6]上,这样狙击手只需通过新的瞄准点对准目标就可完成射击动作,省去了分析环境因素、靠经验计算和反复调整旋钮动作的环节,提高了射击效率。

1.2 基本设置

以瞄准镜目镜中心为坐标原点建立坐标系,x轴方向为枪口处与目标连线在水平面上的投影,y轴方向为重力的反方向,z轴方向为水平面上与x轴垂直的方向。弹丸脱离枪口后,在空气中的运动轨迹[7]为一条偏移的弧线,弹丸运动过程中受多种因素影响,主要受重力加速度、空气阻力、风力、弹丸移动速度等因素的影响,其弹道轨迹曲线如图1所示,图中,O点为弹丸脱离枪口的初始点,E点为弹道轨迹的最高点,此时y轴方向速度为0,θ为狙击步枪射角,v0为弹丸脱离枪口后的初速度,v1为弹丸飞行过程中的速度,Fk为空气阻力,其方向与弹丸飞行方向相反,G为重力,始终朝向地面,Fh为横向风力,Fz为纵向风力。

由于弹丸弹道解算的参数由探测系统测定,探测系统只能测量狙击步枪周围的情况,本文作如下设定。

1)重力加速度的设置。

由物理学可知重力加速度与目标到地球质心的距离成反比。狙击步枪的有效射程相对于地球弧长为极小,射程高差相对地球半径为极小,可以推出在狙击步枪的有效射程内,重力加速度基本相同,设置子弹有效射程内重力加速度为同一数值。

2)弹丸受力面的设置。

高精度的狙击步枪设计时为保持弹丸平稳飞行都会使章动角最小化,弹丸在有效射程内能保持平稳的飞行,考虑金属的钢性特征,弹丸在空气中飞行时磨损极小,形状基本不变,设定弹丸迎风面的最大横截面面积为定值。

3)弹丸初始状态。

狙击步枪是高精度武器装备,同一款狙击步枪枪管长度、内径、膛线等结构参数基本一样,弹丸质量、火药份量基本相同,设定子弹击发后弹丸获得的初始速度大小相同,弹丸本身质量相同,最大横截面面积为固定值。

4)空气气象条件的设置。

空气中的气压、气温、湿度和密度对弹道轨迹有一定的影响,考虑到地球空气环境是一个相对稳定的状态,狙击步枪的有效射程相对于地球表面弧线长度为极小,在狙击步枪有效射程内可以设定空气的气压、气温、湿度和密度与枪口处测量的数据相同。

5)风的状态参数设置。

自然界的风是空气流动引起的一种自然现象,它具有一定的流速和方向,风的方向和强度对弹道有一定的影响,在一定时间和范围内,风的方向和强度相对稳定,考虑到狙击步枪从击发到命中目标只需要数秒的时间,利用校正系统校正瞄准点的时间也极短,设定在弹丸有效飞行轨迹内风的方向和强度保持不变。

2 弹道分析

2.1 目标位置与弹丸初始状态

将瞄准镜目镜中心设置为坐标原点,初始位置时,狙击手使用瞄准镜直接瞄向目标M,设置瞄向目标M的射线在水平面的投影方向为x轴,水平面垂直于x轴的坐标轴为z轴,重力反方向对应y轴,如图2所示。

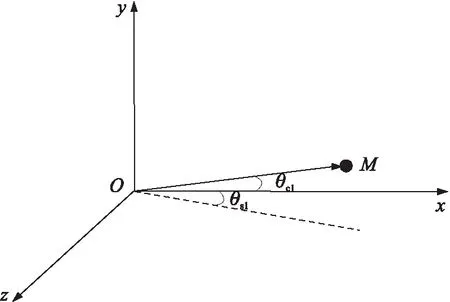
图2 坐标轴的建立

1)目标位置。

测量目标距离时,狙击手通过瞄准镜上激光测距机直接指向目标,设置通过激光测距机测得的坐标原点与目标的距离为L,通过角度测量仪器测得的目标水平角度为θs1,垂直角度为θc1,如图2所示,水平角度0°线对应图2中Oxz平面内的虚线,设置目标的坐标为(xm0,ym0,zm0),目标在x轴上坐标值xm0对应的是射击距离。目标坐标位置的计算公式为

(1)

2)弹丸初始状态。

①初始位置。按照枪支的结构设置枪口与目镜中心垂直距离为h,枪管方向与目镜中心的水平距离为s,设基本位置为瞄准镜瞄向x轴方向时,此时枪口坐标为(s,h,0),如图3中实心圆点N′所示。由于本文研究的是弹丸的外弹道,弹丸外弹道的起点位于狙击步枪枪口处。当瞄准镜初始瞄向目标时,设弹丸初始位置坐标为(x0,y0,z0),如图3中实心圆点N所示。由几何关系可以得出弹丸初始坐标位置的计算公式为

图3 弹丸的初始位置

(2)

②初始速度。高精度狙击步枪枪管的构造、材质,弹丸的形状、质量、火药质量等基本一样,在一定温度下,弹丸从枪口射出后初速度大小基本相同,设子弹初速度为v0,在各坐标轴上的速度分量为vx0,vy0,vz0,其计算公式为

(3)

2.2 弹道轨迹分析

2.2.1 子弹受力分析

子弹在火药推力作用下产生一定动能和初速度,在空气中运动主要受空气阻力、重力和风力的影响。其表示式为

Fa=Ff+Fk+mg

(4)

式中:Fa为弹丸综合受力情况,Fk为空气阻力,Ff为风力,m为子弹质量,g为重力加速度。

空气阻力[8-9]与弹丸的前进方向相反,包括摩擦阻力、涡流阻力和波动阻力,阻力的大小与空气的密度、弹丸迎风面的横截面积、飞行速度和阻力系数等因素有关,表达式为

(5)

式中:CD为阻力系数,ρ为空气密度,S为弹丸迎风面最大横截面积,v为子弹飞行速度,vf为风速,|v-vf|为弹丸相对于风的速度大小。

弹丸所受风力与风速、弹丸移动速度和弹丸横截面积有关,风对弹丸运动轨迹的影响包括横风、逆风和顺风,计算公式为

(6)

结合牛顿第二定律,弹丸的运动轨迹方程为

(7)

现实中使用风速测量仪测量地球表面风速、风向时,垂直于地表的分量比平行于地面的风小很多,在忽略垂直地表风的情况下,弹道解算方程[8]简化为

(8)

2.2.2 参数分析

为计算出子弹的轨迹方程,需要确定式(8)中的各个参数,主要包括固定参数和可变参数。式(8)中的最大横截面积S、子弹质量m、子弹初速为已知参数,枪支设计、生产和试验时已确定,可作为固定参数。可变参数包括空气密度、阻力系数、相对风向。

①空气密度。空气都具有一定湿度、温度,在探测到温度、湿度后,在一定的大气压力下能计算出空气的密度,空气密度与湿度的关系[8]表达式为

(9)

式中:p为大气压力,Rq为空气常数,α为绝对湿度,T为热力学温度。

空气中气压与海拔高度变化[8]的关系式为

(10)

式中:p0为地面大气压力,y为高度。

②阻力系数。弹丸飞行速度逐步减小,阻力系数[10]CD与弹丸的速度有关。阻力定律[11]给出了阻力系数与速度的关系,如图4所示。阻力系数的变化主要分为4个阶段,第Ⅰ阶段为亚音速阶段,Ma<0.8,阻力系数CD几乎为固定常数;第Ⅱ阶段为跨音速阶段,0.8Ma>1.2,CD开始逐步减小至平稳;第Ⅳ阶段为数倍超高音速阶段,Ma>2.8,CD趋于平稳值。由于本文研究的狙击步枪有效射程内弹丸的移动速度为420～840 m/s,基本在第Ⅲ阶段,主要采用第Ⅲ阶段阻力系数和速度的关系式。

图4 阻力系数与速度的关系

③相对风向。相对风向是风与弹丸运动方向的夹角,考虑现实中风速垂直于地表的分量比平行于地面的分量小很多,本文只考虑水平面的风,相对风速、风向可由风速风向测量仪测得,设风与弹丸运动方向的夹角为θ1,风速为vf0,在坐标轴上速度矢量为(vfx,0,vfz),其计算公式为

(11)

3 算法实现

3.1 弹道解算实现

本文弹道解算实现基于Matlab进行,其过程为编写弹道解算代码,输入测量参数,迭代运行计算,达到x轴射击距离时停止计算,输出所需数据,步骤如下。

①代入固定参数。以某型狙击步枪为例,该狙击步枪子弹击发后弹丸获得的初速、弹丸质量、弹丸最大横截面积为固定值,将这些固定参数输入到弹丸弹道解算方程组。

②编写弹道解算代码。弹道解算代码中涉及的方程组包括弹丸的运动方程、弹丸初始速度、位置计算方程、大气密度的计算方程和阻力系数与弹丸速度的计算公式,将5个方程组使用Matlab语言进行编写代码,形成弹道解算代码。

③输入变量参数。部分影响弹道轨迹的参数不是固定值,实际射击过程中需要通过探测器测得,如计算空气密度需要气压、温度、相对湿度和海拔高度的数据,计算弹道轨迹需要射角、风速、风向、重力加速度、弹丸初始位置、速度和目标距离的数据,将以上需要通过探测器探测的数据作为可变参数输入到弹道解算代码中。

④输出数据。变量参数输入到弹道解算代码后,系统进行迭代计算,当达到x轴上射击距离时停止计算,根据系统设定输出弹道轨迹的数据图或数据表格。

3.2 自动校正分析

自动校正算法涉及的方程与弹道解算方程基本一致,但变量参数不同,自动校正算法中弹丸的偏移量为输入参数,枪支的射角为输出参数,与弹道解算算法相反。与弹道解算相比,枪支射角校正后弹丸的初速度向量和所受风力向量有所变化,其他参数不变。

3.2.1 偏移量

由2.1.1节得知狙击手通过直接瞄准目标,测得目标的坐标为(Lcosθc1,Lsinθc1,0),设定x轴向距离Lcosθc1为射击距离,在直接瞄准目标的射角下,经弹道解算系统计算出弹丸在x轴射击距离下的坐标为(Lcosθc1,Lsinθc1+h1,h2),此时h1为y轴上的偏移量,h2为z轴上的偏移量。

3.2.2 校正后变量分析

狙击步枪校正后,弹丸的初速大小、弹丸质量、弹丸最大横截面积保持不变,风力大小、目标距离、重力加速度等影响弹道轨迹的参数与校正前数据一样,因狙击步枪射角的调整,狙击手采用校正后瞄准点射击时,弹丸初始位置速度向量和所受风力向量有变化。

①校正后弹丸初始位置速度向量。

按照弹道偏下瞄准点向下调、偏左向左调的原则,校正后枪支调整的角度可由角度测量仪器测量,设置调整射击角度后角度测量仪器测得水平角度为θs2,垂直角度为θc2,弹丸校正后初始位置速度为v1,在各坐标轴上的速度分量为(vx1,vy1,vz1),其计算公式为

(12)

②校正后初始位置风力向量。

校正后因枪支调整射角,弹丸所受风力角度有变化,其调整的角度为θs2-θs1,设置校正后初始位置子弹受横向风力为Fh1,纵向风力为Fz1,计算公式为

(13)

3.2.3 射击精度分析

校正后的弹道轨迹一般与目标坐标点有一定偏差距离,目标的坐标点难以完全在修正后的弹道轨迹上。为此在系统中设定y轴上偏移量和z轴上偏移量允许的偏差值为Θ。校正后将修正的弹丸初速度矢量、风力矢量代入到弹道解算代码,计算得出弹丸y轴上的偏移量h1和z轴上的偏移量h2,当|h1|<Θ且|h2|<Θ时表示校正有效。

3.2.4 寻优分割法调整射角

为使校正后的偏移量在设定的偏差范围内,本文通过寻优分割法调整射角。以Oxy平面为例,如图5所示,设置A处为狙击手直接瞄准目标的初始位置,枪支垂直射角为θc1,B处为校正后射角,枪支垂直射角为θc2,调整角度差为Δθc=θc2-θc1。校正后的偏移量有3种情况。

图5 狙击步枪调整的射角简图

①当|h1|≤Θ,说明枪支调整射角符合精度要求,校正有效。

3.3 自动校正实现

由于校正后弹丸初速变量和承受风力变量是一个变化值,系统校正时需要通过多次迭代计算才能够使偏移量接近或与目标坐标点重合。自动校正实现步骤如下:

①设定偏差值。根据狙击步枪射击精度的要求,设定校正后弹丸偏移量允许的偏差值Θ。

②编写自动校正算法代码。将调整射角后弹丸初速度变量和承受风力变量计算公式代入弹道解算方程组,按照Matlab的编程语言规则对方程组进行编码,得到自动校正算法代码。

③输入偏移量。在初始位置上由弹道解算系统计算得出相应射击距离上的偏移量,将校正前探测得到的风速、风向、重力加速度、弹丸初始位置、目标的距离和偏移量作为变量参数输入到自动校正代码中进行迭代运算,计算得出枪支需要调整的射角。

④计算校正后偏移量。将枪支调整后的射角代入到弹道解算代码中迭代运算,当迭代计算到x轴上射击距离时停止计算,得出校正后y轴和z轴的坐标值及偏移量。

⑤偏移量对比。将校正后的y轴、z轴偏移量代入到系统设定的偏差值范围进行比较,当偏移量在允许的范围内时,确定枪支调整的射角。当不在偏差值允许的范围内时,执行下步动作。

⑥调整射角。当偏移量不在允许的范围内时,由寻优分割法计算枪支需要调整的射角,重复步骤4和步骤5的动作,直到偏移量在系统设定允许的范围为止。

⑦确定瞄准点位置。确定狙击步枪需要调整的射角后,根据瞄准镜的结构由几何关系计算出瞄准镜上瞄准点的位置,将瞄准点通过光电技术以十字架或红点的形式投影到瞄准镜上,这样狙击手通过校正后的瞄准点直接瞄准目标即可完成射击动作。其流程图如图6所示。

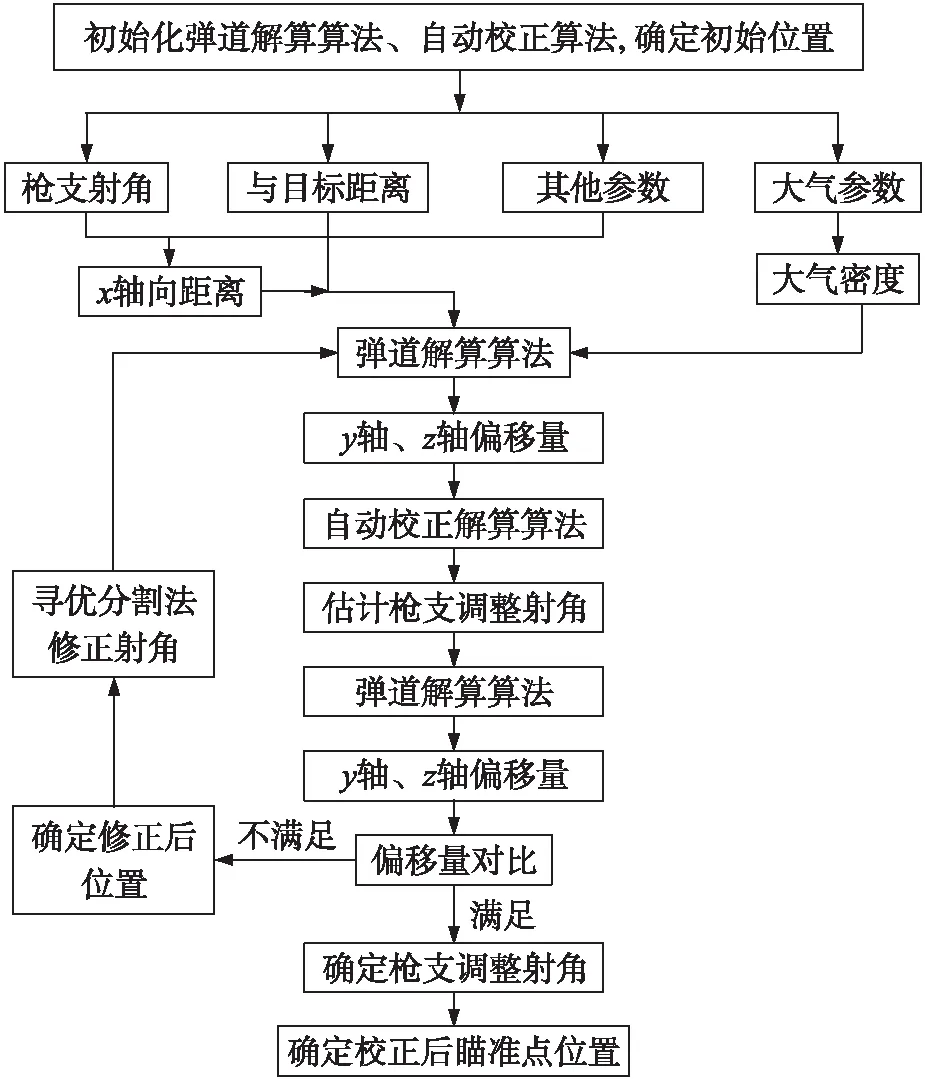
图6 自动校正流程图

3.4 实验对比

为验证自动校正算法的正确性,以某型狙击步枪为例进行仿真研究,设定空气温度20 ℃,海拔高度10 m,弹丸离开枪口初速825 m/s,弹丸质量45.8 g,风速2.5 m/s,风向90°,枪口与瞄准镜目镜中心水平距离0.8 m,高度0.06 m。在同等射击条件下,将弹道解算系统计算的弹道轨迹和狙击步枪弹道表确定的弹道轨迹进行比对,对比情况如图7,可以看出,弹道解算中的轨迹与弹道表对应的轨迹基本一样,在1 000 m距离上水平偏移量相差约0.3 cm,竖直偏移量相差约1 cm。

图7 弹道解算与弹道表的轨迹对比图

为验证自动校正算法的正确性,以某型狙击步枪为例,对800 m射击距离弹着点偏高40 cm进行校正瞄准点,自动校正系统通过输入800 m射击距离、40 cm偏差量计算瞄准点,校正后结果显示枪支垂直射角需向下调整0.03°,水平角度向右调整0.04°,瞄准点校正后以十字或光点形式在瞄准镜上投影,十字光点向上移动0.03°,向左移动0.04°,放大后自动校正瞄准点投影,如图8所示。

图8 自动校正系统校正后的瞄准点

狙击手靠人工计算需要调整瞄准镜上下、左右旋钮。通过查看狙击弹气象和弹道变化的修正量,对比表中数据,确定800 m距离、5 m/s横风时弹道需修正0.08°,2.5 m/s时需修正0.04°。垂直偏移量的修正公式如式(14),设置修正角度为θ,弹着点偏移距离为h3,射击距离为L3,其计算公式为

θ=60h3/L3

(14)

按照偏上向上调的原理,瞄准镜上下旋钮需向上调整0.03°,左右旋钮需向左调整0.04°,与使用自动校正系统调整枪支射角一样。

4 结束语

本文对狙击步枪弹丸有效射程轨迹内的受力情况进行了分析,研究了空气阻力、重力、风和弹丸速度等因素对弹丸运动轨迹的影响,基于Matlab对弹丸的弹道解算算法和自动校正算法进行实现,以某型狙击步枪为例,将弹道解算算法计算的弹道轨迹和弹道表进行了比对,结果表明两者曲线基本一致。在一定横风情况下和弹道偏差量的基础上,由狙击手计算瞄准点和自动校正计算瞄准点进行比对,结果表明自动校正算法校正的瞄准点与狙击手计算的瞄准点调整结果一样,验证了本文弹道解算算法和自动校正算法的正确性。

科学技术的发展使各类传感器、探测器向小型化、微型化发展,未来将所需的各类传感器、探测器、解算算法集成安装到狙击步枪瞄准设备中,狙击手可以通过校正的瞄准点直接瞄准目标,省去了狙击手判断环境因素和靠经验计算的环节,训练一名合格狙击手的周期也将大幅缩短,为新一代狙击步枪瞄准设备的研究提供了方向。