带微型扰流片旋转稳定弹外弹道建模与仿真
杨 杰,刘 丹,常思江
(1.南京理工大学 能源与动力工程学院,江苏 南京 210094;2.西北工业集团有限公司 设计二所,陕西 西安 710043)
随着现代战争和科学技术的发展,在现代战争中实现精确打击和减小附带损伤已经成为必然要求,考虑到效费比,因此针对常规弹药进行制导化改造成为必然趋势。目前,针对155 mm旋转稳定弹等常规弹箭进行的制导化改造主要体现在对引信的改进上,典型代表有精确制导组件(precision guidance kit,PGK)。随着研究的不断深入,有学者提出利用扰流片作为控制机构,并对降落伞、翼型、弹箭等多种模型进行改进,研究了扰流片对这些模型的影响和控制能力[1-2]。
国外相关研究机构和学者针对将扰流片应用于弹箭控制这一问题,包括尾翼稳定弹和旋转稳定弹,提出了具体的结构设计概念,并进一步做出实物模型,进行了相关试验和仿真分析。针对尾翼弹,MASSEY等[3-5]提出利用固定扰流片作为超声速弹箭的控制机构,通过六自由度弹道仿真,验证了该方案能够有效减小攻角振荡,并通过试验证实了实际应用中的可行性。DYKES等[6]考虑在尾翼弹的尾翼之间安装微型扰流片,研究表明弹体、尾翼和扰流片之间的边界层激波相互作用对扰流片所产生的可控力和力矩产生了倍增效应,扰流片能够产生实质性的控制作用,能够消除因炮口扰动、空气动力不确定性和随机风引起的落点误差。SCHEUERMANN等[7]通过计算和实验,估算了弹丸有、无扰流片时的气动系数,研究了尾翼弹在装有扰流片下的控制能力,结果表明该机构在超音速尾翼弹的控制上具有很大的应用前景。刘凯[8]针对某尾翼弹研究了扰流片对流场等的影响,并对其结构进行了优化分析和仿真分析。针对旋转弹,美国陆军研究实验室的FRESCONI等[9]基于40 mm旋转稳定弹提出几种带扰流片旋转稳定弹的结构设计方案,通过实验验证了该结构可靠的性能。文献[10]通过实验和数值计算得到空气动力数据,研究了扰流片的结构参数与修正能力之间的关系。WEY等[11]在弹丸船尾安装滚转解耦的扰流片,通过空气动力分析和七自由度弹道仿真说明了该方案的作用原理和可靠的性能。ROGERS[12]通过研究发现,扰流片在亚音速范围内具有一定的控制效率,随着马赫数的增加,控制效率呈指数级增加,该机构对高超声速弹丸的控制研究具有重要意义。
由于扰流片的存在使旋转稳定弹产生了气动非对称,而现有文献对动力学建模的过程描述不是特别详细,并未具体给出考虑气动非对称效应的建模过程,对控制力和力矩缺乏深入的分析和研究。对此,本文在我国外弹道理论体系[13]下,建立带扰流片旋转稳定弹的动力学模型并进行仿真分析,研究其速度特性、稳定性和修正能力,以期为今后研制该类弹箭提供相应的理论依据。
1 控制原理
弹丸结构如图1所示,扰流片安装在弹丸后体部分,前体与后体通过轴承连接。弹丸未发射时,扰流片收缩在后体控制舱内,全弹外表与普通旋转弹相同。弹丸发射后,扰流片暂不弹出,飞行过程中后体通过电机反转,与前体形成差动旋转,而前体保持较高转速以保证全弹陀螺稳定性。当弹丸飞行到预定区域后,后体通过电机反转至稳定状态后相对空间不转,扰流片展开,提供所需的控制力和控制力矩。

图1 带扰流片旋转稳定弹结构示意图
由于扰流片质量和体积都很小,可忽略质量不对称,并假设控制过程无延迟。扰流片展开后,弹丸整体产生气动不对称,形成附加的阻力、升力和力矩,其中附加力矩提供主要的弹道修正能力。
2 飞行动力学模型
由于带扰流片旋转稳定弹后体结构简单,为研究方便,在建模过程中忽略其后体质量,故无控时动力学模型与普通六自由度弹道模型无异;扰流片展开后产生附加的控制力和控制力矩,在无控动力学模型的基础上构成有控动力学模型。为减小篇幅,本文不再赘述无控动力学模型所包含的力和力矩[13],仅对扰流片产生的附加力和力矩进行建模。
2.1 坐标系
在建模过程中,除需要用到外弹道学中常用坐标系外[13],还应对前、后弹体分别建立前体坐标系Ox1y1Fz1F和后体坐标系Ox1y1Az1A,其坐标原点分别位于前体和后体。图示坐标原点重合,如图2所示。前体坐标系Ox1y1Fz1F与常规弹体坐标系Ox1y1z1重合,而后体坐标系Ox1y1Az1A则是在前体坐标系基础上将Oy1F轴和Oz1F轴绕Ox1轴转动角度Δγ得到,Δγ为差动滚转角,有:
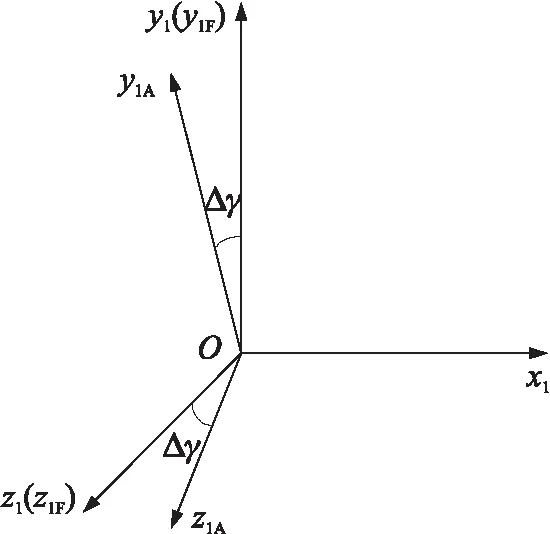
图2 前体坐标系与后体坐标系
Δγ=γA-γF
(1)
式中:γA,γF分别为后体和前体的滚转角,γF与弹体滚转角γ相同。
图3为零攻角时作用于后体的附加力和力矩示意图,设沿弹轴从弹尾向前看有一垂直于弹轴的横截面,假设扰流片位于后体坐标系Oy1A轴位置,γS为扰流片方位角,ΔFx为附加阻力,ΔFy为附加升力,ΔMz为附加力矩。

图3 零攻角时附加力和力矩示意图
图4为各矢量、平面与弹轴坐标系示意图,vr为相对速度,δr为相对攻角,Λ为扰流片方位的单位矢量,Λ与vr构成一相对平面,称之为Λ-vr平面,用点线表示,Θ表示Λ与vr的夹角。vr与ξ轴构成相对攻角平面,用虚线表示,A为相对攻角平面在Oηζ平面上投影的位置,如图4所示。vrη,vrζ为vr在η轴、ζ轴上的投影,γr为攻角平面相对弹轴坐标系Oη轴转过的角度,从Oη轴算起,顺时针为正,如图5所示。
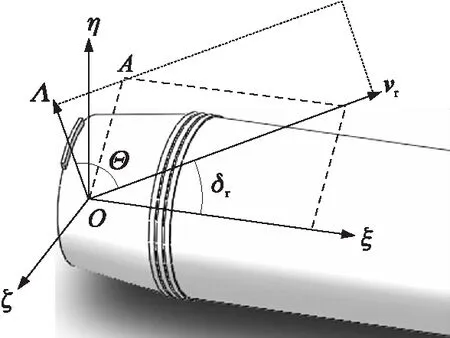
图4 角度和平面关系示意图
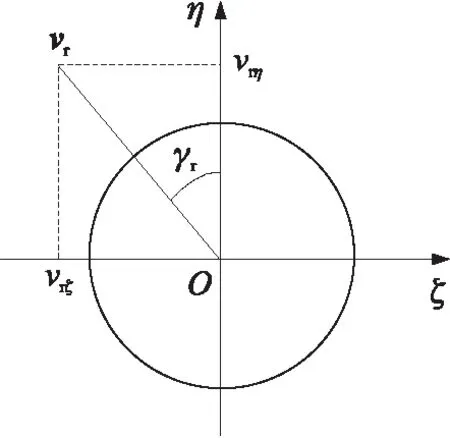
图5 攻角不为零时攻角平面示意图
2.2 扰流片产生的附加阻力
扰流片展开后会产生附加阻力ΔFx,其沿相对速度矢量vr的反方向,其大小需用vr的值计算,矢量表达式为
(2)
式中:ρ为空气密度,S为弹丸参考面积,Δcx为附加阻力系数。
附加阻力在弹道坐标系的分量为
(3)
式中:ΔFxx2,ΔFxy2,ΔFxz2为附加阻力沿弹道坐标系的分量;vrx2,vry2,vrz2为相对速度沿弹道坐标系的分量。
2.3 扰流片产生的附加升力
扰流片展开,会造成弹体气动不对称,从而产生附加升力。假设附加升力在Λ-vr平面内并垂直于相对速度vr,与扰流片在vr的同一侧,如图2和图3所示,可表示为
(4)
式中:Δcy为附加升力系数,Δcy=Δc′yδr,Δc′y为附加升力系数导数。化简得到:
(5)
根据图3,可以得到关系式cosΘ=sinδrcos(γS-γr),代入式(5)并转换到弹道坐标系,有:
(6)
式中:ΔFyx2,ΔFyy2,ΔFyz2为附加升力沿弹道坐标系的分量;δ1为高低攻角;δ2为方向攻角;γr可根据相对速度分量之间关系求得:
(7)
根据式(6)可知,当攻角为0时,式中第一项为0,而第二项不为0,其值随扰流片滚转角改变而改变,充分体现了扰流片产生气动非对称效应,在攻角为0时仍能产生附加升力。
2.4 扰流片产生的附加力矩
弹丸通过调节扰流片滚转角γS,提供所需的俯仰控制力矩和偏航控制力矩,附加力矩方向与Λ-vr平面垂直。其表达式为
(8)
扰流片控制力矩在弹轴坐标系上的投影为
(9)
式中:Δmz为附加力矩系数,Δmz=Δm′zδr,Δm′z为附加力矩系数导数,l为弹丸参考长度。
由式(9)可知,当攻角不为0时,控制力矩沿弹轴的分量并不为0,因此会产生一定影响。由于该力矩分量作用在后体,而后体通过反旋电机令γS固定,因此仅对反旋电机提供的力矩存在少量影响。
2.5 刚体弹道模型
根据以上建立的由扰流片产生的附加力和附加力矩模型,得到质心动力学方程和绕心动力学方程为
(10)
式中:Fx2,Fy2,Fzz为除控制力外的合外力在弹道坐标系中的分量;θa为弹道倾角;ψ2为弹道偏角;t为飞行时间;弹丸无控飞行时k=0,有控飞行时k=1;Mξ,Mη,Mζ为除控制力矩外的合外力矩在弹轴坐标系中的分量;ωξ,ωη,ωζ为角速度在弹轴坐标系中的分量;φ2为弹轴方位角;JC为极转动惯量;JA为赤道转动惯量。
3 弹道仿真
本文以某155 mm带微型扰流片的旋转稳定弹为例,通过计算流体力学方法得到Δcx、Δcy和Δmz,见表1,其与扰流片外露高度HS相关,HS为扰流片与弹体连接处至顶部距离。根据以上建立的控制力和控制力矩模型,进行六自由度弹道仿真,分析射角、初速、启控时间及扰流片高度对速度、稳定性和修正能力等的影响。

表1 扰流片气动系数(HS=7.75 mm)
由表1可知,附加升力系数导数为负值,这是因为建模时假设附加升力与扰流片方位一致,但实际计算结果表明其与扰流片方位反向,故为负值。
3.1 速度变化特性
扰流片展开后产生的附加阻力必然会对弹丸速度存在一定影响,仿真结果见图6和图7。图6为初速v0=930 m/s,射角θ0=45°,扰流片外露高度HS=7.75 mm时,不同启控时间tc下的速度对比图;图7为v0=930 m/s,θ0=45°,tc=70 s时,不同HS下的速度对比图。
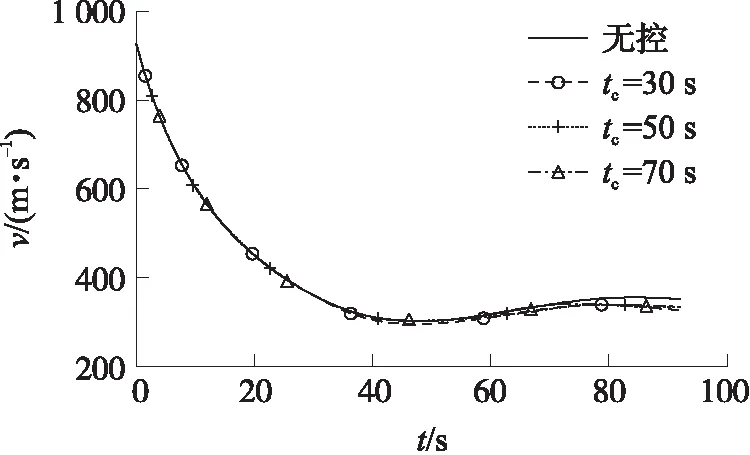
图6 不同启控时间下速度变化曲线对比
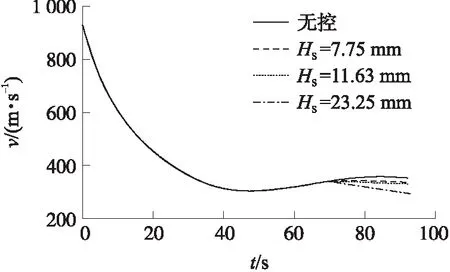
图7 不同扰流片高度下速度变化曲线对比
由图6可知,在不同启控时间下,弹丸速度较无控都有所减小,但变化不大;由图7可知,扰流片外露高度越高,弹丸速度减小越多,速度变化剧烈。
3.2 攻角运动变化规律
弹丸运动稳定性与角运动密切相关,通过分析攻角运动变化规律研究其稳定性,仿真结果见图8~图11。图8为初速v0=930 m/s,启控时间tc=30 s,HS=7.75 mm时,不同射角下的攻角对比图;图9为射角θ0=45°,tc=30 s,HS=7.75 mm时,不同初速下的攻角对比图。
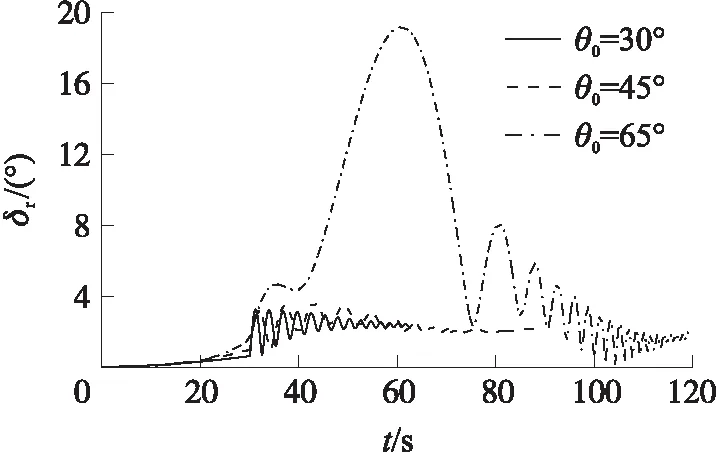
图8 不同射角下攻角变化曲线对比
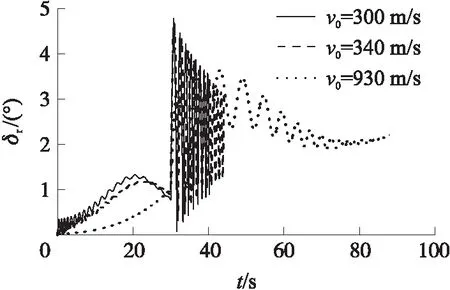
图9 不同初速下攻角变化曲线对比
由图8可知,射角越低,启控前攻角值越小,启控之后攻角振荡幅度越小,收敛速度越快,θ0=65°时,攻角在弹道顶点附近达到将近20°,这对弹丸飞行稳定是非常不利的;而攻角最终收敛值几乎不随射角改变,保持在2°附近。
由图9可知,初速越低,启控前攻角值越大,启控之后攻角变化频率越快,收敛速度没有明显变化;而攻角变化平均值总在2°附近并向其收敛。
图10为v0=930 m/s,θ0=45°,HS=7.75 mm时,不同启控时间下的攻角对比图。由图10可知,分别在弹道上升段和弹道下降段启控时攻角变化呈现出不同特性;而收敛速度无明显差异,攻角最终收敛值几乎也不随启控时间改变,保持在2°附近。

图10 不同启控时间下攻角变化曲线对比
图11为v0=930 m/s,tc=70 s,θ0=45°时,不同扰流片参数下的攻角对比图。由图11可知,随着扰流片外露高度HS的增加,启控瞬时攻角的振荡幅度增大,攻角收敛速度减慢,且最终收敛值也逐渐增加,由0°左右增大到5°左右。

图11 不同扰流片高度下攻角变化曲线对比
由以上分析可知,在扰流片作用下,弹丸攻角最终能够收敛到一定值,弹箭运动趋于稳定,但攻角的收敛值与扰流片高度有关,扰流片高度越高,攻角最终收敛值越大,且收敛越慢,稳定性变差;高射角条件下,若在弹道上升段启控,弹丸在弹道顶点附近的攻角很大,稳定性很差。
3.3 弹道修正能力
下面在地面坐标系[13]下考察带扰流片旋转稳定弹在不同条件下的弹道修正能力,仿真结果见图12~图15。图12为v0=930 m/s,θ0=45°,HS=7.75 mm时,不同启控时间下修正能力对比图;图13为v0=930 m/s,θ0=45°,tc=70 s时,不同HS下修正能力对比图。
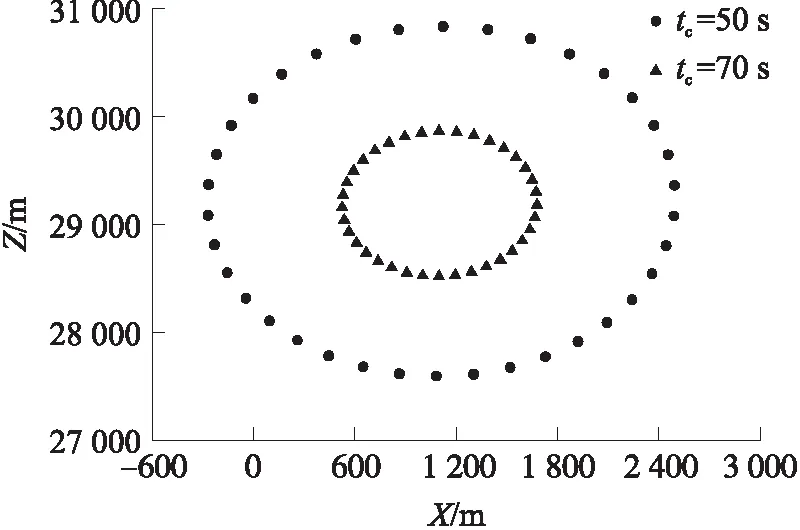
图12 不同启控时间下修正能力对比
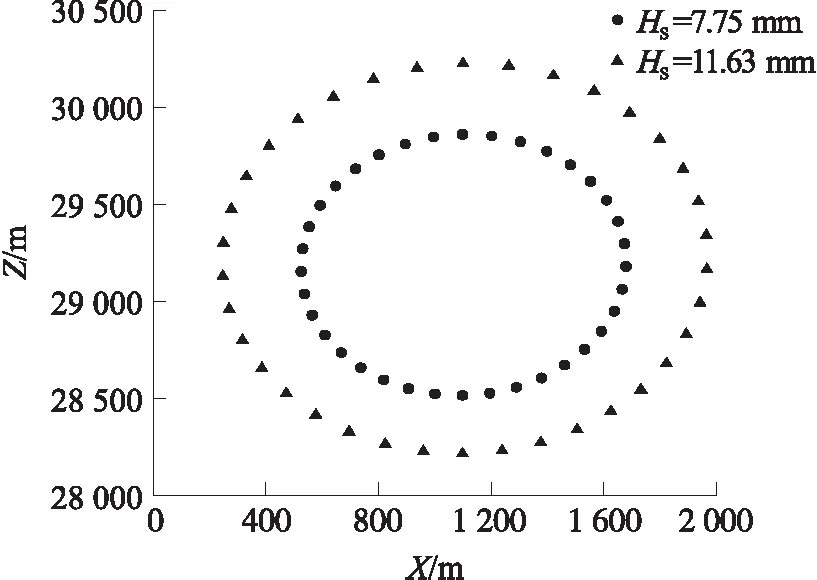
图13 不同扰流片高度下修正能力对比
由图12可知,70 s启控时修正半径为600 m左右,50 s启控时修正半径达1 600 m左右,能够将侧偏Z修正为0,因此启控时间越早,弹丸修正范围越广。
由图13可知,HS=7.75 mm时修正半径为600 m左右,HS=11.63 mm时修正半径达1 000 m左右,由此可见扰流片高度越高,所能提供的修正能力越强。
图14为弹丸从(0,0)点向下运动,在不同初速下5 s内的修正能力对比图。由图14可知,v0=300 m/s时修正半径为17 m左右,v0=340 m/s时有所减小,v0=930 m/s时修正半径为25 m左右,可见随着马赫数的增加,弹丸修正能力并非总是增大,而是在跨音速段有所减小。
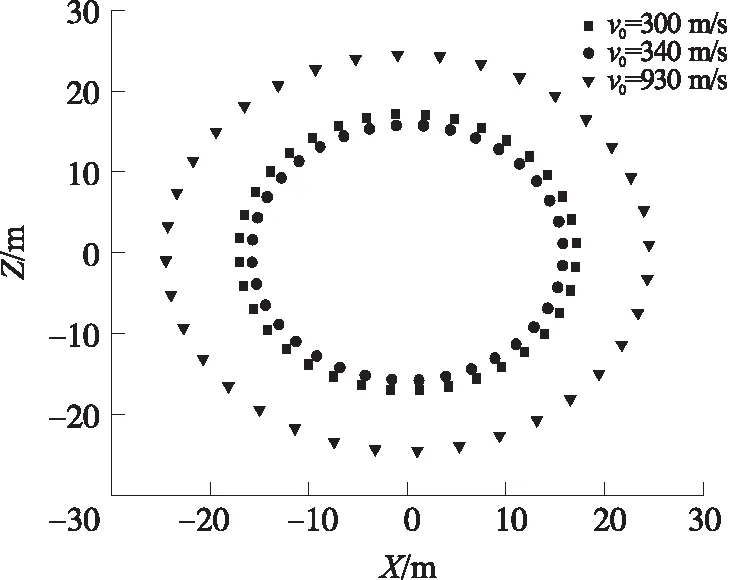
图14 不同速度下修正能力对比
图15为v0=930 m/s,θ0=10°时的无控弹道曲线以及在弹道顶点启控的落点分布图。由图15可知,无控时弹道侧偏大约100 m,而从弹道顶点启控修正半径达到大约400 m,且根据落点分布发现,弹丸修正方向与扰流片作用方位相反。
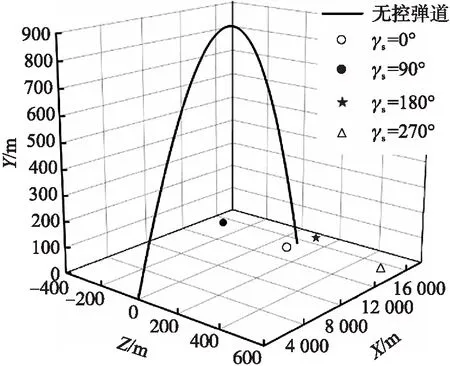
图15 小射角下无控弹道与修正落点
由以上分析可知,扰流片启控时间越早,弹丸修正能力越强,在弹道降弧段启控已经能够满足修正的要求;扰流片高度越高,修正能力越强;随着马赫数的增加,修正能力在跨音速段有所减小,随后又增大。
4 结论
本文以带扰流片旋转稳定弹为对象建立了控制力和控制力矩模型,通过六自由度弹道仿真分析了不同因素对弹丸稳定性和修正能力的影响,得出如下结论:
①在射角、初速、启控时间和扰流片外露高度众多影响因素中,扰流片外露高度对弹丸稳定性的影响最大,扰流片外露高度越高,启控后速度下降越明显,启控瞬时攻角振荡越大,攻角稳定值越大,稳定性越差;高射角和较早的启控点会使弹丸在弹道顶点附近稳定性变差。
②弹丸修正能力受启控时间、扰流片高度和速度的影响,启控时间越早,修正能力越强;随着扰流片高度的增加,修正能力逐渐增强;当马赫数从亚音速向超音速变化时,修正能力在跨音速段有所减小,随后增大。
③弹道修正方向与扰流片作用方位相反,在该类弹丸设计过程中,应当综合考虑弹丸稳定性与弹道修正能力的关系,选取适当的控制参数和弹道参数,在保证稳定性的前提下充分发挥修正能力。

