弹药对典型钢筋混凝土楼房毁伤评估方法研究
周 阳,李向东,周兰伟,邹 杰,纪杨子燚
(1.南京理工大学 机械工程学院,江苏 南京 210094;2.中国航空工业集团公司 洛阳电光设备研究所,河南 洛阳 471003)
现代战争(如海湾、波黑以及科索沃战争等)表明以指挥大楼为代表的地面建筑是弹药攻击的重要目标,毁伤地面建筑的能力越高,赢得战争主动权就越大。及时准确地评估目标毁伤效果,有助于作战指挥员优化火力打击方案、高效配置打击资源,并为制定火力毁伤计划提供科学依据,同时对目标防护的设计与改进也具有重要意义[1-3]。弹药爆炸作用下地面建筑目标的毁伤评估方法大致分为2种:第一种是数值模拟方法,如ELSANADEDY等[4]用LS-DYNA分析了爆炸载荷作用下钢框架建筑结构的破坏情况,姚宇飞等[5]用LS-DYNA分析了爆炸载荷作用下四层两跨钢筋混凝土建筑结构的破坏情况,该方法比较直观,但时间成本较高。第二种是工程计算方法,首先对爆炸过程进行简化,然后使用相应的模型与函数,分析整个毁伤过程并形成计算程序,如美国国防部开发的FACDAP程序[6],TAN[7]开发的BDP程序,李殷[8]开发的预测外爆载荷下建筑毁伤程度程序等,此方法虽不能反映建筑的破坏细节,但计算效率高,能够方便快速得到计算结果,同时保证准确度。现有工程计算方法大多采用直接设置炸点位置计算建筑毁伤,未考虑弹药攻击建筑时弹药不同攻击条件下对炸点位置的影响和弹药落点的散布问题。
针对以上研究的不足,本文建立了一种楼房毁伤评估方法,并在此基础上设计开发了可计算弹药在任意攻击条件下对楼房毁伤效能的程序。通过该程序计算了楼房建筑在侵爆弹作用下的易损性,同时结合弹药散布规律求解了弹药在命中误差下对楼房毁伤程度的期望值,并分析了弹药不同攻击条件对楼房毁伤期望的影响,可为战时制定火力打击计划提供技术支撑。
1 楼房与弹药模型
1.1 楼房模型
建筑类型多种多样,有建筑材料的不同,如钢筋混凝土、钢材、木材等,也有结构的不同,如框架结构、剪力墙结构等。本文针对建筑中最常见的钢筋混凝土楼房,建立侵爆弹对其毁伤的评估方法。楼房建筑物通常由楼板、柱、梁、墙等构件组成,如图1所示,钢筋混凝土楼房长、宽、高分别为20 m、15 m、12 m,共4层,每层由12个房间构成,房间大小5 m×5 m×3 m,构件参数如表1所示。

图1 楼房模型

表1 构件参数
1.2 弹药模型
打击建筑类目标的弹药主要是侵爆弹,侵爆弹利用其动能侵入建筑物内并爆炸,爆炸形成的冲击波破坏建筑构件。本文以某侵爆弹为例,计算其对楼房的破坏作用,侵爆弹相关参数如表2所示。

表2 弹药参数
2 弹药对楼房的侵彻及爆炸载荷
2.1 弹药炸点位置
弹药撞上楼房后,延迟引信触发,假定弹药运动过程中弹道不发生偏转,如图2所示,其侵彻楼房时,可视为弹药侵彻多个间隔混凝土构件。

图2 弹药侵彻楼房示意图
弹药首先侵彻构件1,弹药侵彻构件1时可利用YOUNG公式[9]计算其侵彻深度H1,如果h1/cosφ1>H1,则弹药未能穿透构件,弹药从构件1入射位置运动至极限侵彻深度H1位置的时间t1近似为
t1=2H1/vi
(1)
式中:vi为弹药入射速度;h1为构件厚度;φ1为弹药入射角。
如果引信延迟时间td≥t1,则炸点位置位于弹道线上极限侵彻深度H1处;反之则位于弹道线上距构件1上弹药入射位置vitd/2处。
如果h1/cosφ1≤H1,根据动态空腔膨胀模型,弹药侵彻过程中所受阻力为
F=πd2(Rr+BNρv2)
(2)
式中:F为弹药侵彻时所受平均阻力;d为弹药直径;Rr为与静阻力有关的静阻力参数;B为靶板材料压缩系数,混凝土取1;N为弹药头部形状系数;ρ为靶板密度;v为弹体瞬时速度。
由牛顿第二定律和初始条件可得:
(3)
式中:mp为弹药总质量。
对式(3)左右两边积分,可得侵彻速度随时间变化的关系为
(4)
对式(4)积分可得侵彻位移xp随时间变化的表达式为
(5)
通过式(4)与式(5)可计算,当弹体侵彻位移xp=h1/cosφ1时,弹药的运动时间t1与剩余速度v1。
如果td≤t1,则炸点位置位于弹道线上距构件1弹药入射位置(vi+v1)td/2处;反之弹药穿透构件,进入空气1中,引信延迟时间更新为td1=td-t1。
假设弹药在空气中运动时速度无衰减,则弹药穿过空气1所需时间t2为
t2=da1/v1
(6)
式中:da1为弹道线上构件1上弹药穿出位置与构件2上弹药入射位置之间的距离。
如果td1≤t2,则炸点位置位于弹道线上距构件1上弹药穿出位置v1td1处;反之弹药进一步侵彻构件2,弹药入射速度等于穿透构件1后的剩余速度v1,引信延迟时间更新为td2=td1-t2。
在构件2中弹药的运动计算方式与构件1中一致,如此往复计算则可得到弹药最终炸点位置。
2.2 弹药爆炸载荷计算模型
弹药爆炸时能量主要消耗在2个方面,一是使弹药壳体破碎,二是压缩周围空气形成冲击波;弹药对楼房的毁伤主要来自爆炸产生的冲击波,弹药装药消耗在冲击波上的等效TNT质量me为[10]
(7)
式中:f为炸药的TNT当量系数;mc为弹药装药质量;ms为弹药壳体质量。
冲击波对构件的入射超压、比冲量、正压时间均可由下式计算[11]:
S=exp{A+BT+CT2+DT3+ET4+FT5+GT6}
(8)

3 构件毁伤计算
3.1 构件毁伤准则
爆炸载荷作用下楼房不同构件的变形情况均可采用等效单自由度方法[12]计算。以梁构件为例,如图3(a)所示,假设冲击波载荷均匀加载到梁表面,同时冲击波压力-时程曲线简化为图3(b)所示三角形,此时可用梁中点位置表示梁的变形情况,图3(a)可简化为如图3(c)所示的等效单自由度体系。

图3 等效单自由度方法
根据牛顿第二定律,等效单自由度体系的运动方程为
(9)

构件的毁伤程度一般由支座转角确定,支座转角与构件中点位移的关系为
tanθ=2x/L
(10)
式中:L为构件特征尺寸,对于梁、柱构件,为构件长度;对于墙、板构件,由于其中央位置处塑性屈服铰线一般平行于长度方向,如图4所示,此时L为构件宽度。
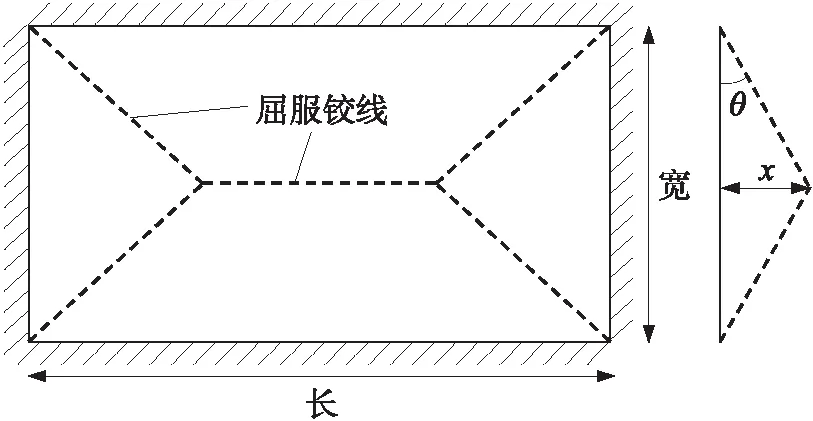
图4 板构件塑性铰示意图
根据文献[13],当构件支座转角大于12°时构件完全破坏,可得构件破坏时中心的临界位移为
xc=(Ltan12°)/2
(11)
当式(9)计算所得的构件中心最大位移大于式(11)计算所得的临界位移时,认为构件破坏。
3.2 墙后构件毁伤计算
楼房内部构件较多,墙后构件由于墙体遮挡,所受爆炸载荷与无墙遮挡时的爆炸载荷大相径庭。如图5所示,此时无法使用式(8)直接计算墙2所受冲击波载荷。
无墙1遮挡时,弹药爆炸后假设作用在墙2上的冲击波能量完全转化为墙体的动能,则作用在墙2上的冲击波能量为
(12)
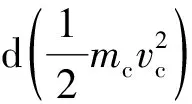

图5 墙后冲击波计算示意图

ke=i2a2b2/(2ρh2)
(13)
式中:i为无墙1遮挡时墙2处的冲击波比冲量;a2,b2,h2分别为墙2的长、宽、高;ρ为墙体密度。
有墙1遮挡时,假设冲击波破坏墙1时墙体吸收的冲击波能量完全转化为墙体的内能,墙1破坏时墙的内能U为
U=FRxc
(14)
式中:FR为墙1的抗力;xc为墙破坏时中心的临界位移。
根据能量守恒定律,有墙1遮挡时墙2处的冲击波能量ke,n为
ke,n=ke-U=[i2b2a2/(2ρh2)]-FRxc
(15)
墙2处的冲击波比冲量为
(16)
假设墙2处的冲击波载荷正压持续时间仍为弹药在空气中爆炸时该距离处持续时间t+,同时在冲击波载荷简化为图3(a)所示的三角载荷下,可得有墙1遮挡时墙2处的冲击波超压为
pn=2in/t+
(17)
求得墙2处冲击波特征参数后即可使用等效单自由度方法计算墙2毁伤与否。
4 楼房毁伤评估
已知楼房构件毁伤情况后,下面计算楼房整体毁伤情况。定义毁伤构件体积与楼房所有构件体积之比为楼房毁伤程度PK为
(18)
式中:Nb为破坏构件数量,Vr为第r个破坏构件的体积,Nt为楼房构件总数,Vs为第s个构件的体积。
以上即为指定弹药攻击位置上楼房毁伤程度的计算方法,但是弹药存在命中误差,计算弹药对楼房的毁伤时需考虑弹药命中误差对毁伤结果的影响,对此可通过计算弹药在不同位置处的命中概率以及命中该位置时楼房的毁伤程度,从而得出弹药对楼房的毁伤期望。如图6所示,将楼房投影于弹药指定攻击方向垂直的平面上,认为弹药未命中楼房时楼房不毁伤,因此计算毁伤时只考虑楼房投影的包络矩形范围。

图6 弹药攻击方向上楼房投影
打击楼房时弹药瞄准点一般位于投影包络矩形中点,弹药命中位置服从均值为0,方差相等的二维正态分布,同时在x与y向上命中概率互相独立,其概率密度函数g(x,y)为
(19)
式中:标准差σ=δCEP/1.177 4,δCEP为弹药圆概率误差。
然后对楼房投影的包络矩形划分网格,在网格足够小的情况下,可认为网格内弹药命中概率密度相等,弹药命中网格内的任意位置处,楼房的毁伤程度相等。取网格中心处命中概率密度为网格内平均命中概率密度,弹药攻击网格中心时楼房的毁伤程度为网格内的平均毁伤程度。则弹药对楼房的毁伤期望E(PK)为
(20)
式中:q为单元个数;g(xw,yw)为第w个网格中心处的命中概率密度;Aw为第w个网格的面积;PK,w为弹药命中第w个网格中心时的楼房毁伤程度。
5 典型楼房建筑物毁伤评估
5.1 楼房毁伤评估计算
以楼房地面中心为原点O,平行于楼房地面长边为yg轴建立图7所示右手直角坐标系,其中v0为弹药终点速度,弹药速度方向与地面夹角为弹药高低角θ,速度方向在地面上的投影与yg轴夹角为弹药方位角ψ。对楼房进行毁伤评估计算时,分别以弹药终点速度v0、高低角θ、方位角ψ作为变量,计算楼房毁伤情况;终点速度v0分别取200 m/s,250 m/s,300 m/s,350 m/s及400 m/s;高低角θ分别取0°,15°,30°,45°,60°,75°及90°,方位角ψ取值方式与高低角θ一致。

图7 弹药攻击示意图
图8所示为部分楼房投影毁伤程度分布图,左侧为楼房在弹药攻击平面上的投影,右侧为弹药命中不同网格时楼房的毁伤程度分布。

图8 楼房投影与毁伤程度分布图
图8(a)所示为θ=90°,v0=300 m/s时楼房投影的毁伤程度分布,无方位角是因为θ=90°时,楼房投影与方位角无关。可以看出楼房毁伤程度呈中心对称分布,这是由于弹药垂直地面攻击楼房时,楼房本身对称则炸点位置对称,毁伤程度分布也对称。同时楼房毁伤程度在投影中心位置处较高,边缘位置较低也基本符合实际情况。多个房间相连处毁伤程度较高,这是因为冲击波破坏墙体时会有较大的能量衰减,对墙后构件的毁伤能力也会下降;对于有限的冲击波能量,在能破坏当前房间的情况下,炸点位置离墙体越近,则墙后所剩的冲击波能量越大,对墙后构件的毁伤能力也越强,楼房总体毁伤程度也越高。图8(b)所示为θ=60°,ψ=90°,v0=300 m/s时楼房的毁伤程度分布,此时弹药攻击方向不垂直于楼房表面,但多个房间相连处毁伤程度也较高。在楼房投影上侧边缘与下侧边缘处楼房毁伤程度较低,这是因为弹药攻击方向与地面不垂直,弹药攻击楼房上、下两侧边缘处弹药爆炸时炸点位置已在楼房外,下侧边缘处毁伤程度更低是因为弹药攻击上侧边缘时弹药在空气中爆炸,攻击下侧边缘时弹药在楼房地面以下的土壤中爆炸,冲击波能量衰减比在空气中更快。
5.2 楼房毁伤结果
弹药在不同攻击条件下对楼房的毁伤期望如图9、图10所示。
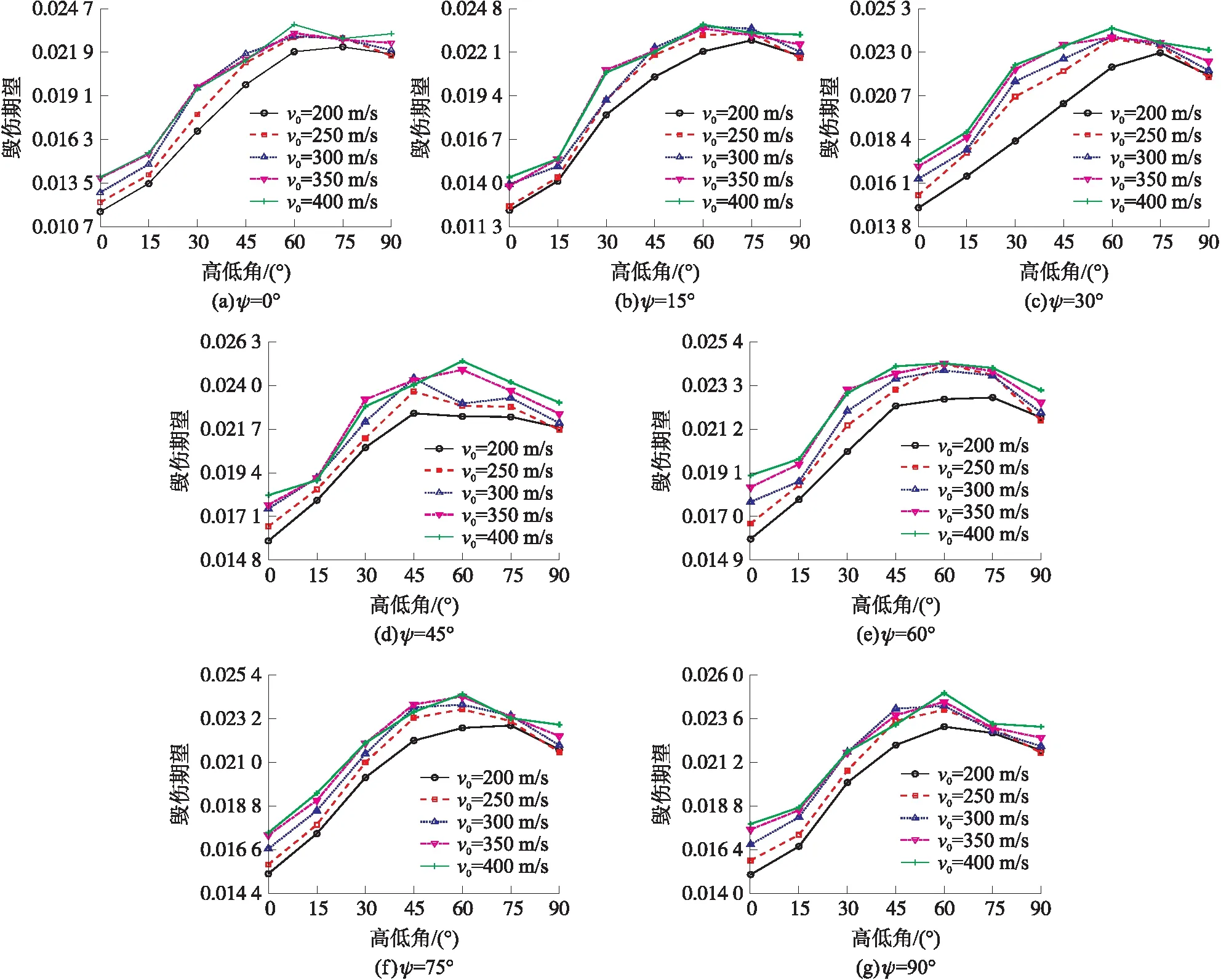
图9 弹药不同方位角ψ下楼房毁伤期望
图9为弹药在不同方位角ψ下对楼房的毁伤期望分布图。可以看出,在不同方位角下,弹药对楼房毁伤的期望随高低角的变化规律比较一致,期望值随着高低角增加先增加后减小,这可能是因为在不同的方位角下,楼房投影面积都随着弹药高低角先增加后减小,在弹药命中误差一定的条件下,投影面积越大,弹药命中目标的概率越大,相应的毁伤期望也越大。在方位角与高低角一致的情况下,终点速度越高,毁伤期望基本也越高。图9(a)所示为方位角ψ=0°时的毁伤期望分布,此时最大值为0.023 69,出现在高低角θ=60°,终点速度v0=400 m/s处。图9(b)所示为方位角ψ=15°时的毁伤期望分布,此时最大值为0.023 72,出现在高低角θ=60°,终点速度v0=400 m/s处。图9(c)所示为方位角ψ=30°时的毁伤期望分布,此时最大值为0.024 24,出现在θ=60°,v0=400 m/s处。图9(d)所示为方位角ψ=45°时的毁伤期望分布,此时最大值为0.025 28,出现在θ=60°,v0=400 m/s处。图9(e)所示为方位角ψ=60°时的毁伤期望分布,此时最大值为0.024 37,出现在θ=60°,v0=350 m/s处。图9(f)所示为方位角ψ=75°时的毁伤期望分布,此时最大值为0.024 68,出现在θ=60°,v0=400 m/s处。图9(g)所示为方位角ψ=90°时的毁伤期望分布,此时最大值为0.024 94,出现在θ=60°,v0=400 m/s处。可看出毁伤期望最大值基本都出现在θ=60°,v0=400 m/s处,为此时楼房投影面积较大所致;不同方位角下最大值相差较小,其中最大的毁伤期望为0.025 28。
图10所示为弹药在不同高低角θ下对楼房的毁伤期望分布图。可以看出,在不同高低角下,弹药对楼房毁伤的期望随方位角的增加也大致先增加后减小,可能也是因为楼房投影面积随着方位角先增加后减小的原因。在高低角θ=90°时,毁伤期望随着方位角的增加无变化是因为此时方位角对楼房的投影无影响,投影一致则毁伤期望一致。
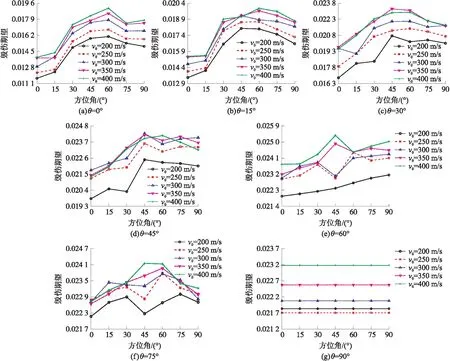
图10 弹药不同高低角θ下楼房毁伤期望
图10(a)所示为高低角θ=0°时的毁伤期望分布,此时楼房投影面积较小,因此毁伤期望也较低,最大值仅为0.019 07,出现在方位角ψ=60°,终点速度v0=400 m/s处。图10(b)所示为高低角θ=15°时的毁伤期望分布,此时楼房投影面积也较小,最大值为0.019 85,出现在方位角ψ=60°,终点速度v0=400 m/s处。图10(c)所示为高低角θ=30°时的毁伤期望分布,此时最大值为0.023 27,出现在方位角ψ=45°,终点速度v0=350 m/s处。图10(d)所示为高低角θ=45°时的毁伤期望分布,此时最大值为0.024 37,出现在方位角ψ=45°,终点速度v0=300 m/s处。图10(e)所示为高低角θ=60°时的毁伤期望分布,此时最大值为0.025 28,出现在方位角ψ=45°,终点速度v0=400 m/s处。图10(f)所示为高低角θ=75°时的毁伤期望分布,此时最大值为0.024 17,出现在方位角ψ=45°,终点速度v0=400 m/s处。图10(g)所示为高低角θ=90°时的毁伤期望分布,此时最大值为0.023 2,出现在终点速度v0=400 m/s处。可看出毁伤期望的最大值基本出现在方位角45°~60°,终点速度300~400 m/s之间,也因为此时楼房投影面积较大所致;不同高低角下最大值相差较大,说明高低角的变化对此楼房毁伤的影响大于方位角,可能是不同高低角下,楼房投影面积变化较大所致。
6 结束语
本文基于工程计算模型建立了一种弹药打击下对钢筋混凝土楼房毁伤评估的方法,该方法不仅可计算弹药任意指定攻击位置下对楼房的毁伤效能,也可计算弹药在命中误差下对楼房的毁伤期望。同时构建了钢筋混凝土楼房与侵爆弹模型,基于所建立的毁伤评估方法计算了弹药在不同攻击条件下对楼房的毁伤效能,验证了其可行性与有效性。该方法适用于弹药打击地面楼房建筑等作战任务场景,可快速、实时计算出弹药不同攻击条件下对楼房建筑的毁伤效能,有助于得出弹药对目标的最佳攻击条件,提高弹药利用率,也可为制定作战计划提供技术支撑。

