基于摄动落点预测与修正比例导引的复合修正算法设计

柯知非,高 敏,王 毅,宋卫东

(1.北京跟踪与通信技术研究所,北京 100094;2.陆军工程大学 导弹工程系,河北 石家庄 050003)

修正控制算法是指弹丸在飞行过程中所需遵循的规律,它的性能直接关系到弹丸命中目标的精度。对于二维弹道修正,适用于旋转稳定弹的修正控制算法可大致分为方案控制算法与导引控制算法。方案控制算法可分为弹道成形(trajectory shaping)、预测控制(predictive control)、弹道跟踪(trajectory tracking)3种,而适用于修正能力有限的弹道修正弹丸的修正控制算法仅有后两种[1]。

JITPRAPHAI等[2]在基于脉冲修正的火箭弹上,研究了TT制导、PNG制导和PAPNG制导,通过仿真对比各方案的修正效能,文献[3]研究了落点预测法和修正比例导引法,得出利用落点预测法进行制导的关键:通过实时预测落点位置计算零效脱靶量(ZEM)。

以上各种方案中,弹道追踪法对弹载计算机的计算性能要求不高,相对而言是较为容易实现的[4]。文献[5]采用该导引律对155 mm榴弹的操纵性进行了分析。然而,该方法未考虑修正控制过程中弹丸的速度信息,弹丸沿基准弹道的不断穿越使修正控制的总能量产生大量消耗。何光林等[6]最早针对一维修正弹落点预报原理,对采用正交多项式拟合弹道和误差补偿的方法降低预报落点的偏差等进行了研究,为研究其他修正方式和二维弹道修正弹的落点预测方法提供了借鉴。黎海青等[7]针对固定翼控制的双旋结构旋转稳定弹,建立了七自由度运动方程,利用四自由度(4D)质点弹道模型设计了落点预测制导律,将该制导律用于旋转稳定弹修正控制,大幅减小了落点散布。文献[8]通过直线外推落点和带重力补偿直线的方法对脉冲末修迫弹进行脱靶量预测研究,进一步提高了落点外推算法的精度。田再克等研究分析了摄动理论落点预测在弹道修正弹上的应用[9-13],该理论在满足弹道修正实时性要求的基础上能较好地提高射击精度与减小落点散布。杨泗智等[14]在高旋火箭弹平台上利用了落点预测法进行弹道修正,该方法能有效地减小落点的圆概率误差(CEP),但受于炮弹引信修正能力的限制,需要做进一步的优化。王钰等[15]通过综合摄动理论落点预测法与修正质点弹道预测法计算速度与精度的特点,提出了结合两种方法的分段预测法,通过仿真得出了优于单一预测方法的结论。文献[4]在双旋弹上通过对比修正比例导引法和弹道追踪法,研究得出修正比例导引在横向上的修正效果更易受到测量误差的影响,但其所需存取信息更少,修正比例导引相对优于弹道追踪法,但弹道追踪法的准确度相对更高。

本文在前人研究的基础上,针对装有基于固定鸭舵式二维修正组件的旋转稳定弹,提出一种在弹道上升段采用摄动落点预测,下降段采取变系数修正比例导引的复合导引律,该算法综合了2种方法的优点,既实现上升段的修正控制,又可以实现降弧段对目标点的闭合,提高了射击精度。

1 修正控制特性

如图1所示,固定鸭舵式二维弹道修正组件由一对相同舵偏角的反向减旋舵与一对相同舵偏角的同向控制舵组成,为单通道控制。由于组件的舵偏角固定,弹丸在飞行时通过控制修正组件同向舵的相对于地面的滚转角实现弹道修正。

图1 固定鸭舵式二维弹道修正组件外形示意图

文献[16]对修正弹偏流特性的研究发现:由于陀螺效应,弹轴将运动到控制角的反方向右侧,即获得与控制角方向相反的动力平衡角和垂直该平面向右的动力平衡角,并获得相应的弹道修正量。即弹道的修正控制量相对于控制角存在一定的相位滞后,该相位滞后影响着控制信号的生成。不同发射初速、射角、修正持续时间、滚转角对相位滞后存在一定影响[17],本文所涉及修正弹在对应装药的初速和射角上较为固定,受以上因素影响较小,故对以上项目统一进行拟合。

该滞后角与弹丸飞行马赫数成一定关系,通过多项式拟合得出:

φz=-285Ma4+1 638Ma3-3 517Ma2+3 352Ma-1 032

(1)

式中:φz为滞后相位角,Ma为马赫数。

2 修正算法设计

2.1 摄动落点偏差预测

假定X0(x0,y0,z0)和XT(xT,yT,zT)分别为发射系中发射点和目标点坐标。若弹丸初速和射角一定,则在不加入任何干扰的情况下命中目标点的弹道曲线是唯一的,该弹道即为基准弹道。然而,弹丸飞行过程中,由于弹丸自身参数偏差、气动参数偏差、风等干扰因素的存在,弹道将偏离基准弹道形成弹丸落点的偏差,称该弹道为扰动弹道。

定义XT=Φ(x,y,z,vx,vy,vz)为基准弹道的函数表达式,函数以x为自变量,以vx,vy,vz,y,z为状态变量,且函数在任意一点连续可微。令XIm(xIm,yIm,zIm)为扰动弹道的落点。若落点XIm与目标点XT距离较近,可在基准弹道任一点X(x,y,z)处采用泰勒展开的方法计算扰动弹道的落点坐标(仅给出二阶泰勒展开),即:

(2)

式中:Φx,Φz分别为射程和横偏的函数;Xp=(ΔvxΔvyΔvzΔyΔz)T;Δvx,Δvy,Δvz,Δy,Δz为射程x处的状态变量的偏差量;V=(vxvyvz);Rx(X,V),Rz(X,V)分别为落点纵向坐标xIm、横向坐标zIm泰勒展开的拉格朗日余项。

式(2)整理可得:

(3)

式中:ΔL,ΔH分别为纵向、横向的落点偏差。

2.2 变增益修正比例导引

若目标静止XT(xT,yT,zT),弹丸在空中任意位置为X(x,y,z),则可得弹丸在竖直平面和水平面内的视线转率分别为

(4)

(5)

式中:θcx,n,σcx,n分别为当前时刻的弹道倾角程序角、弹道偏角程序角;θcx,n-1,σcx,n-1分别为上一时刻的弹道倾角程序角、弹道偏角程序角;Kθ,Kσ分别为竖直平面和水平面内的比例系数;Δt为两时刻的时间间隔。

当前时刻弹道倾角和弹道偏角分别为

(6)

式中:θn,σn分别为当前时刻的弹道倾角、弹道偏角;vn为当前时刻弹丸的合速度;vxn,vyn,vzn为弹丸合速度在发射系坐标轴上的分量。

则有:

(7)

式中:Uθn,Uσn为导引信号。通过导引信号与弹丸的控制特性即可给出控制信号。

变增益比例导引中增益系数Kθ和Kσ为变量,其计算方法如下:

①搜索发射高低角和发射方位角,使弹丸精确命中目标点。

②使用如下公式计算Kθ和Kσ的值:

(8)

式中:θn-1,σn-1分别为上一时刻的弹道倾角、弹道偏角。

③得到一组Kθ和Kσ,在有控弹道仿真中使用插值的方法获得相应的比例系数。

④导引系数解算同经典比例导引算法。

该方法的优点在于:在弹道较为弯曲处使用较大的比例系数提供较大的可用过载,使弹道末段的需用过载变小,从而减小脱靶量。然而,此处需要研究的问题是采用哪个变量对比例系数进行插值,可用于插值的变量有飞行时间、射程和动压。

2.3 修正比例导引算法

摄动+比例导引复合导引算法是指将通过摄动方法预测的落点偏差作为补偿量添加至变增益比例导引算法中,进行控制信号的解算,即

(9)

式中:kθ,kσ分别为纵向偏差和横向偏差的补偿系数,系数值的选取需通过仿真分析进行选取。

2.4 控制信号生成

依据文献[16]中滚转导弹的弹体传递函数的建立方法,建立旋转稳定弹丸的弹体传递函数。

(10)

式中:Wθ,Wσ分别为竖直方向和水平方向的弹体传递函数,a22表征弹丸的赤道阻尼力矩特性,a24表征弹丸翻转力矩特性,a25表征控制力矩特性,a′27表征弹体的马格努斯力矩特性,a′28表征弹体的陀螺力矩特性,a34表征弹体的升力特性,a35表征操纵舵产生的控制力特性。

固定鸭舵式二维弹道修正引信采用单通道控制方案,即采用一对鸭舵实现对弹道的纵向和横向修正,因而,需要综合考虑弹丸纵向和横向的传递系数来生成控制角。令A0=Wθ/Wσ,则有:

(11)

式中:γfk为控制角;Uθn,Uσn为使用预测落点偏差补偿后的导引信号,φz为多项式拟合的相位滞后角。

3 仿真分析

3.1 算法精度分析

摄动+比例导引的复合导引算法:弹道上升段采用摄动落点预测法,下降段使用修正的比例导引。该算法以摄动落点偏差预测、比例导引算法和榴弹的控制相位滞后为基础,因而算法误差为三者综合作用的结果。本文通过仿真的手段对算法精度进行分析。

首先通过搜索射角、射向使弹道精确命中目标,然后采用搜索所得的射角、射向进行修正弹的弹道仿真,仿真得到落点与目标点的偏差即为算法误差。需要指出的是,仿真中不添加随机扰动,且制导控制系统在理想状态下工作,即制导控制系统无任何误差。

弹道的仿真条件如表1所示,标准气象条件下,弹丸以40.5°发射,称2条弹道分别为基准弹道和有控弹道,如图2所示。发射系中基准弹道和有控弹道的落点坐标分别为(2 5987.7 m,0,823.557 m)和(25 988.9 m,0,826.388 m),两者的纵向偏差和横向偏差分别为1.2 m和2.831 m。两落点间的距离为3.075 m,即为算法误差。

表1 基准弹道仿真参数设定

图2 算法精度分析

为进一步验证修正能力对算法精度的影响,进行了如下的仿真分析。通过调整影响弹丸无控落点散布的因素的偏差量,减小弹丸无控落点散布,而后进行有控打靶。若有控状态下,落点散布CEP较小,则说明算法精度较高。仿真结果如图3所示。

图3 算法精度分析

经调整影响落点散布的偏差量,无控状态下落点散布的纵向和横向标准差分别为121.061 7 m和11.377 0 m,CEP为78.320 8 m;有控状态下,纵向标准差和横向标准差分别为3.717 1 m和4.039 2 m,CEP为4.603 2 m。该仿真结果充分说明,弹丸的修正能力制约了落点的修正控制精度,摄动+比例导引的复合导引算法的精度很高。

3.2 有控弹道仿真

目标点距26 km,弹丸初速为897 m/s,且仿真中不添加随机干扰。经搜索,弹丸以40.5°射角发射时可精确命中目标,以此弹道为基准弹道。修正弹射角为39.5°,其弹道为有控弹道。仿真结果如图4～图7所示。

图4 射程-弹道高曲线

图5 射程-横偏曲线

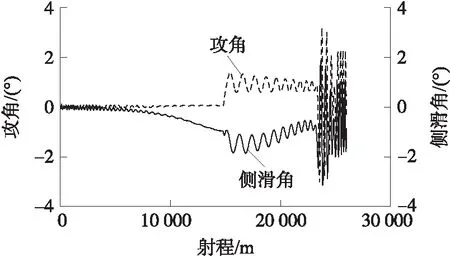
图6 攻角和侧滑角曲线

目标点在发射系中的坐标为(25 987.7 m,0,823.557 m),有控弹道落点坐标为(25 982.1 m,0,818.813 m),落点纵向偏差和横向偏差分别为-5.6 m和-4.744 m。由图5可知,有控弹道攻角从起控前的0°附近阶跃至起控后的1°,侧滑角的平均位置在数值上仅增加了0.2°左右,与理论分析一致。在23～25 km段,攻角、侧滑角曲线变化频率较高,但振幅不超过2°,该现象由控制信号的抖动引起。攻角、侧滑角振幅在2°以内验证了弹丸的稳定性。

3.3 蒙特卡洛打靶

图7为采用摄动+比例导引算法的弹丸的打靶结果,打靶中仅考虑弹丸的随机扰动。落点的纵向标准差为22.835 7 m,横向标准差为23.579 2 m,CEP为27.507 0 m。图中,修正能力曲线内的点在修正控制下均能精确命中目标,修正能力曲线外的点在不断地向目标点逼近,且充分发挥了弹丸的修正能力。仿真结果表明,摄动+比例导引的复合导引算法可有效应用于修正弹的制导控制系统。

图7 随机扰动下的落点散布

4 结束语

采用固定鸭舵式二维弹道修正组件对传统弹药引信进行替代,是实现大口径炮弹低成本弹道修正的重要途经。本文综合摄动落点预测与修正比例导引算法:上升段运用摄动落点预测进行横向修正,降弧段采用修正比例导引算法进行综合修正。研究结果表明,该算法精度较高,在采用一标准射击条件下,算法误差仅为3.075 m,且弹丸的修正能力制约了落点的修正控制精度。采用本文所用复合导引算法可有效提高该修正弹的射击精度,减小射击落点散布。