弹道解算用数值天气预报风修正系数辨识

曹树新,李 岩,李帅孝,徐树威

(1.南京理工大学 能源与动力工程学院,江苏 南京 210094;2.陆军装备部 沈阳地区军事代表局驻沈阳地区第二军事代表室,辽宁 沈阳 110004;3.齐齐哈尔建华机械有限公司,黑龙江 齐齐哈尔 161006)

随着快速机动能力的不断增强和侦察校射技术的不断发展,现代战争对火炮的快速反应能力提出了更高要求,气象保障作为火炮射击保障的核心环节之一,有必要在提升气象保障的速度和精度方面加以研究[1]。近年来,数值天气预报在火炮气象保障中的应用极大缩短了气象保障的准备时间[2-5],但是,初始场测量处理误差和数值模式建模误差,使得数值预报结果中含有较大的预报误差,且尤以风的预报误差最为显著[6]。现行有效的数值修正方法以数值天气预报的预报误差及其变化规律为依据,对临近天气预报的预报误差进行数值修正[7],提升气象要素的预报精度。因此,如何快速准确获取预报误差已成为提升弹道解算用数值天气预报的预报精度需首要解决的问题之一。

目前,利用成熟的火炮外弹道跟踪观测技术获取的实测弹道数据,为快速准确获取弹道解算用数值天气预报的预报误差提供了新途径。本文为获取风的预报误差,使用风修正系数描述风的预报误差,提出一种采用无迹卡尔曼滤波算法,直接从实测弹道数据和原始预报气象数据中辨识风修正系数的方法,并通过数值比对和弹道重构,对风修正系数的辨识精度进行分析。

1 系统模型

1.1 WRF模式简介及参数设置

WRF(weather research and forecast,WRF)模式是由美国多家科研机构于2000年开发的新一代中尺度数值模式和数据同化系统,其广泛应用于中小尺度到全球尺度的数值预报和大气模拟,并可提供指定区域在未来时段内的时空网格化气象数据。

本文中WRF模式预报区域位于我国东北地区的松嫩平原,该区域为温带大陆性季风气候,太阳辐射充足。模式水平方向上采用单重网格结构,格点数为121×121,格点间距为4 km,垂直方向上分为81层,模式顶层气压为1 000 Pa,初始场使用NCEP发布的分辨率为0.25°×0.25°的再分析资料,积分步长为15 s,预报时长为4 h。

1.2 假设条件

影响弹丸飞行状态的气象要素包括气压、虚温、纵风和横风,为了具体分析弹道解算用数值天气预报的气象保障效果,本文以WRF模式的短时预报为例,一方面使用均方根误差、平均绝对误差和误差标准差[8]对WRF模式预报的气象要素进行检验,另一方面,基于外弹道仿真,分析WRF模式中单一气象要素的预报误差对弹丸飞行状态的影响。其中,预报气象数据和实测气象数据描述的均为该地2019年12月14日12时的高空大气状态,外弹道仿真则使用某型榴弹的六自由度刚体弹道模型,射角为51°,射向为100.487°,射程约为30 km。WRF模式预报气象要素的检验结果如表1所示,WRF模式单一气象要素的预报误差对弹丸飞行状态影响的分析结果如表2所示。

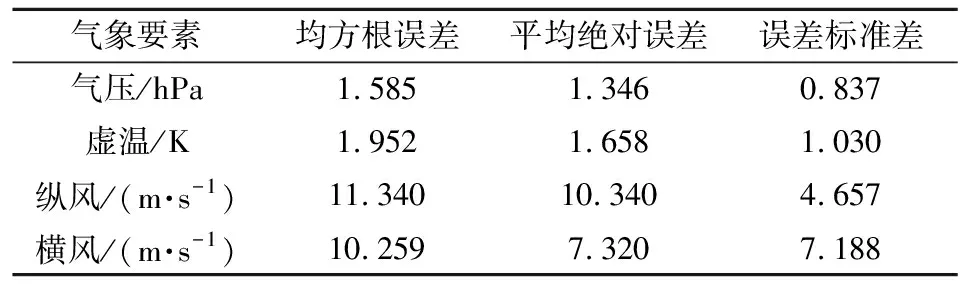
表1 WRF模式预报气象要素检验结果

表2 弹丸飞行状态偏差均值表

由表1和表2可得,相比于风的预报误差,气压和虚温的预报误差及其离散程度以及预报误差引起的弹道偏差均相对较小,因此,本文只将风修正系数作为待辨识参数,并忽略气压和虚温的预报误差对辨识风修正系数的影响,故本文做出如下假设:

①忽略气压和虚温的预报误差对辨识风修正系数的影响;

②风修正系数在辨识区间内为常值。

1.3 弹道模型

为了从实测弹道数据和原始预报气象数据中辨识风修正系数,需构建弹丸运动模型,建立实测弹道数据与气象数据之间的联系。考虑到目前弹道跟踪观测数据主要以位置和速度为主,本文选用质点弹道模型,此弹道模型在有风条件下的弹道方程[9]为

(1)

式中:

x、y、z,vx、vy和vz分别为弹丸在发射坐标系下的坐标分量和速度分量;m,d,l和JC分别为弹丸质量、弹丸直径、弹丸长度和弹丸极转动惯量;Cx,C′y,m′z和m′xz分别为空气阻力系数、升力系数导数、静力矩系数导数和极阻尼力矩系数导数;p,Tv,wx,wz,vs,Rd和k分别为当地气压、当地虚温、当地纵风、当地横风、当地声速、干空气气体常数和比热比;kL和kC分别为纵风修正系数和横风修正系数;g,v0,s和η分别为当地重力加速度、标定初速、弹道弧长和膛线缠度。

2 无迹卡尔曼滤波算法辨识风修正系数

为了实现从非线性弹道模型中辨识风修正系数,本文将无迹卡尔曼滤波算法作为辨识算法。由卡尔曼滤波稳定性原理[10]可知,如果滤波稳定,估计值和估计均方误差将随滤波时间的增长逐渐不受滤波初值的影响,并最终收敛,实现无偏估计。但是,每个估计值和每个估计均方误差的收敛速度不同,若滤波时间较短,可能存在估计值和估计均方误差没有完成收敛的情况。因此,本文将原始预报气象数据作为弹道模型的基础气象条件,采用无迹卡尔曼滤波算法对实测弹道数据进行迭代处理,并将每次迭代所得风修正系数和状态变量的估计均方误差作为下次迭代的初值,直至满足迭代终止条件,其流程如图1所示。

图1 无迹卡尔曼滤波算法辨识风修正系数流程图

由式(1)和实测弹道数据的种类可知,无迹卡尔曼滤波算法中的观测变量为x、y、z,vx、vy、vz,状态变量为x、y、z,vx、vy、vz、kL和kC,即:

Z=(xyzvxvyvz)T

(2)

X=(x1x2x3x4x5x6x7x8)T=

(xyzvxvyvzkLkC)T

(3)

将式(3)代入式(1),得:

(4)

结合图1,无迹卡尔曼滤波算法辨识风修正系数的主要步骤如下。

①第1步。选定初值。

②第2步。无迹卡尔曼滤波计算,详细计算步骤可参考文献[10]。

③第3步。判断是否满足迭代终止条件,若没有满足,则返回第2步。为了提高迭代效率,本文设置2个迭代终止条件,条件一为达到最大迭代次数nmax,条件二为连续2次迭代所得纵风修正系数之差εL和横风修正系数之差εC均小于给定阈值。

为了提升辨识结果精度,减小包括气动参数误差和起始扰动误差在内的其他误差对辨识结果的影响,本文将弹丸风洞吹风数据作为弹道模型中气动参数的真值,并将多组辨识结果的平均值作为最终的辨识结果。

3 数值计算与分析

为了检验无迹卡尔曼滤波算法辨识风修正系数的效果,本文基于某实测弹道数据和WRF模式原始预报气象数据对其进行数值分析,相关参数设计如下。

①实测弹道数据的位置误差(DRMS,68%):水平10 m,垂直10 m;速度精度(DRMS,68%):水平0.2 m/s,垂直0.5 m/s;

②弹道数据选择距地面5 200～6 800 m的降弧段弹道数据;

③WRF模式参数设置与第1.1节中的参数设置相同;

④无迹卡尔曼滤波算法迭代终止条件一为最大迭代次数nmax=200,迭代终止条件二为连续2次迭代差值εL<0.000 1且εC<0.000 1。

基于上述参数,本文以其中一组实测弹道数据为例,在辨识过程中x、y、z的估计均方误差随迭代次数n(取前10次,下同)的变化如图2所示,vx、vy、vz的估计均方误差随迭代次数的变化如图3所示,kL、kC的估计均方误差随迭代次数的变化如图4所示,kL、kC随迭代次数的变化如图5所示。

图2 迭代过程中的位置估计均方误差

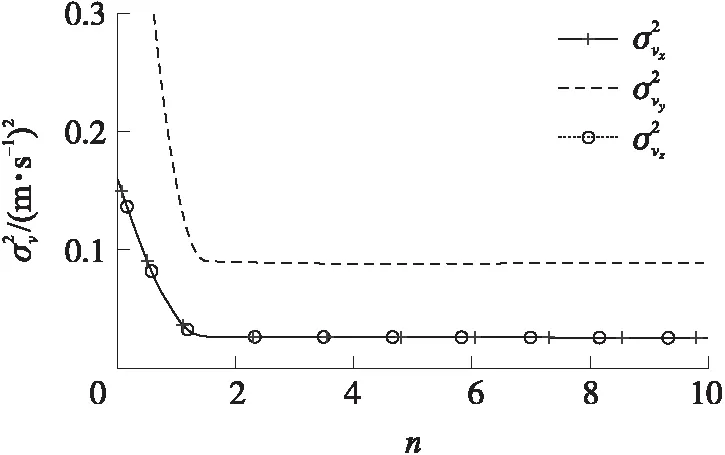
图3 迭代过程中的速度估计均方误差

图4 迭代过程中的风修正系数估计均方误差

将3组辨识结果取平均值作为该辨识区段内的辨识结果,即辨识的纵风修正系数为2.084 056,横风修正系数为1.254 748。实测的风修正系数如表3所示,使用加权平均值(权重由弹丸在每个高度段内的飞行时间确定,下同)代表实测的风修正系数,即实测的纵风修正系数为1.944 045,横风修正系数为1.206 837。

表3 实测的风修正系数

将实测的风修正系数和辨识的风修正系数进行对比可得,辨识的纵风修正系数和横风修正系数的相对误差分别为7.20%和3.97%,产生上述误差的原因可能如下:一是辨识过程中未考虑气压和虚温的预报误差对辨识风修正系数的影响,将气压和虚温的预报误差折算入风修正系数当中;二是弹道模型误差,结合六自由度刚体弹道模型可知,状态变量还受弹丸姿态角等因素的影响,而质点弹道模型未考虑这些因素;三是实测气象数据与实测弹道数据时空不匹配。

原始预报气象数据和实测气象数据描述的均为同一时刻且同一地点的高空大气状态,利用前文辨识所得的纵风和横风的修正系数对原始预报气象数据中的风进行修正,得到修正预报气象数据,3种气象数据中风的加权平均值如表4所示。

表4 弹道区段内风的加权平均值

由表4可得,原始预报气象数据中的纵风和横风经修正后,其误差分别减小85.19%和79.27%。

分别使用原始预报气象数据和修正预报气象数据对位于距地面5 200～6 800 m的降弧段弹道进行重构,2种重构的弹道段和滤波处理的实测弹道段在x-y平面的投影如图6所示,在x-z平面的投影如图7所示,在z-y平面的投影如图8所示,2种重构的弹道段与滤波处理的实测弹道段间的状态均方根误差如表5所示。

图6 重构弹道段在x-y平面的投影

图7 重构弹道段在x-z平面的投影

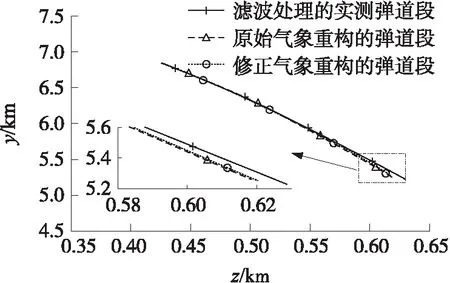
图8 重构弹道段在z-y平面的投影

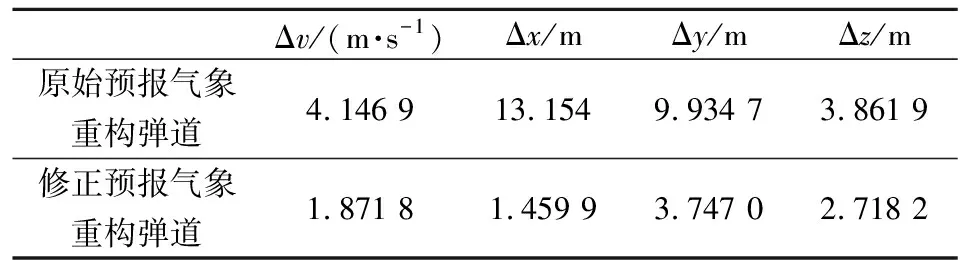
表5 重构弹道段的状态均方根误差

由图6～图8及表5可得,修正预报气象重构的弹道段相比原始预报气象重构的弹道段而言,更加接近于滤波处理的实测弹道段,因此,修正预报气象比原始预报气象对真实气象的描述更为准确,从而说明辨识所得风修正系数的精度较高以及修正弹道解算用数值天气预报的预报误差是必要的。

4 结束语

本文将原始预报气象数据作为基础气象条件,采用无迹卡尔曼滤波算法从实测弹道数据中辨识风修正系数,通过对实际辨识结果进行分析,得出以下结论:该方法辨识所得风修正系数具有较高的精度,可作为弹道解算用数值天气预报的预报误差,实现对临近天气预报的数值修正,满足工程应用需求;无迹卡尔曼滤波算法在辨识风修正系数的过程中兼有滤波功能,能够在一定程度上减小噪声对辨识结果的影响。本文研究结果可以为提升弹道解算用数值天气预报的预报质量提供一定的理论参考。