复合材料座钣动态响应分析及结构优化

葛建立,谢新宇,刘国志,杨国来

(1.南京理工大学 机械工程学院,江苏 南京 210094;2.山西北方机械制造有限责任公司,山西 太原 030009)

迫击炮主要由炮身、炮架、座钣、瞄具等构成,是一种短炮身、大射角、弹道弧线高、发射带尾翼弹的曲射火炮,能够对近距离上的目标实施压制和摧毁,是支援和伴随步兵作战的一种重要武器装备。

随着现代战争形势的转变和科学技术的发展,降低迫击炮质量,提高重型迫击炮的便携性和机动性,是现代迫击炮发展的重要趋势。由于座钣直接承受迫击炮发射时的后坐阻力,座钣质量在全炮质量中占有很大比重,所以座钣轻量化设计是降低迫击炮质量的重要途径之一。

座钣轻量化研究主要体现在以下几个方面:①基于有限元法的结构优化设计[1],包括尺寸优化、形状优化和拓扑优化,根据优化结果确定座钣结构,进一步提升金属利用系数;②应用轻型材料,如复合材料和钛合金等[2];③组合式座钣研究,组合式座钣虽然无法降低座钣总质量,但是可以将座钣化整为零,以达到单独部件可背运的质量要求。

目前,复合材料在迫击炮座钣上的应用研究较少,但是在其他武器装备轻量化设计中,已经得到了广泛的应用。瑞典军方将轻质钛合金内衬与碳纤维树脂基复合材料外套组合应用在火炮身管上,实现减质25%[3]。俄罗斯将覆盖了芳纶纤维复合材料的均质钢作为面板和背板,将酚醛树脂复合材料作为中间层,制得了T-72主战坦克的轻型复合装甲。英国材料系统实验室对碳纤维复合材料的减轻质量的效果研究表明,利用碳纤维复合材料制作尺寸相近的车身,在保证车身刚强度的情况下减轻约50%[4]。

为了提高大口径迫击炮的便携性和机动性,本文研究碳纤维复合材料座钣的设计,并对座钣的质量和炮口扰动进行优化。

1 复合材料座钣结构设计

传统的金属座钣的各部分一般通过焊接进行连接, 焊缝处往往是结构强度薄弱的地方。使用复合材料制作座钣时,由于复合材料成型工艺的限制,复合材料的形状通常很难像金属材料那样加工为复杂的曲面。如果复合材料座钣的结构设计得比较复杂,那么就难免会出现部分复合材料需要互相连接,其连接处同样也会是结构强度薄弱的地方,为了尽可能减少连接,复合材料座钣的形状不能设计得很复杂,尽量利用现有成熟的复合材料成型工艺做到一体化成型。本文采用一体化成型工艺设计了复合材料座钣,如图1所示。

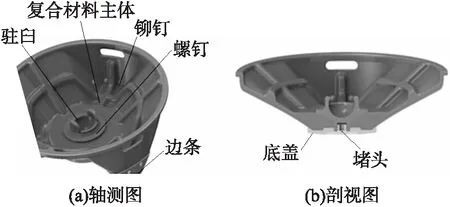
图1 复合材料座钣三维模型

从图1可以看到,本文设计的复合材料座钣由复合材料主体、驻臼、底盖、堵头、边角组成,驻臼、底盖、堵头、边角的材料为钛合金。座钣外形为圆形,3个把手处结构向下凹陷形成梯形凸起,有利于提高射击稳定性。通过增加局部铺层厚度,在复合材料主体上布置加强筋,达到提高座钣整体结构的刚度。

本文选择碳纤维增强环氧树脂基复合材料T300/3231作为迫击炮座钣的主要结构材料。驻臼等金属部件则选择了钛合金TC4。初始方案的座钣质量为34.72 kg。碳纤维复合材料参数[5]如表1所示,钛合金的材料参数如表2所示。表中,E1,E2和E3分别为单向板纵向(沿碳纤维铺层方向)、横向和法向的杨氏模量;G12,G13和G23分别为单向板纵向、横向和法向的剪切模量;ν12,ν13和ν23分别为单向板纵向、横向和法向的泊松比;XT,XC分别为单向板纵向拉伸、压缩强度;YT,YC分别为单向板横向拉伸、压缩强度;S12,S13和S23为单向板3个方向的剪切强度。根据复合材料横观各项同性假设,ZT=YT,ZC=YC。

表1 T300/3231材料参数

表2 钛合金材料参数

复合材料铺层方向可根据单层性能需求进行选取,但过多的铺层方向会使设计和加工复杂化,造成不必要的浪费。0°,90°和±45°为目前最常用的铺层方向。座钣在射击时的实际受力比较复杂,因此根据座钣的承载特性和结构特点,选择[+45/-45/0/90]重复铺层方式[6],每层厚度不超过1.5 mm。

2 复合材料力学失效模型

本文采用的碳纤维复合材料T300/3231由多层单向板组成,每层单向板采用纤维沿同一方向排列的单向复合材料制成,具有非均匀性和各向异性。在各向异性体中,设平面内的方向为1方向、2方向,厚度方向为3方向,则各向异性材料的应力(σ)-应变(ε)关系[7]为

(1)

式中:γ为剪应变,ε为正应变,Cij为刚度系数,Cij满足Cij=Cji;σ为正应力,τ为剪应力。刚度矩阵C可以通过对柔度矩阵S求逆得到。柔度矩阵的表达式为

(2)

根据柔度矩阵的对称性,可得:

(3)

根据碳纤维复合材料的9个独立的材料参数,可以得到柔度矩阵S,对柔度矩阵S求逆得到刚度矩阵C。

复合材料的损伤是一个渐进的过程,并且损伤会导致复合材料的刚度衰减,最终导致材料失效。碳纤维复合材料的损伤可以分为面内损伤和层间损伤,面内损伤包括:纤维拉伸与压缩失效、基体拉伸与压缩失效和基体-纤维剪切失效;层间损伤包括:拉伸、压缩分层失效。目前常用的复合材料失效准则主要有最大应力准则、最大应变准则、Tsai-Wu准则和Hashin准则。本文采用三维Hashin失效准则,判断复合材料层合板的失效,具体描述如下。

①纤维拉伸失效(σ11≥0)。

(4)

②纤维压缩失效(σ11<0)。

(5)

③基体拉伸失效(σ22+σ33≥0)。

(6)

④基体压缩失效(σ22+σ33<0)。

(7)

⑤拉伸分层失效(σ33≥0)。

(8)

⑥压缩分层失效(σ33<0)。

(9)

⑦基体-纤维剪切失效(σ11<0)。

(10)

复合材料刚度退化准则选择Tan退化准则[8],纤维方向与基体方向上不同失效模式下的刚度折减系数,如表3所示。

表3 Tan刚度退化模型的刚度折减系数

本文利用ABAQUS的显式求解模块(Explicit),根据复合材料的应力-应变关系、失效准则及刚度退化规律,编写了用户材料VUMAT子程序用于求解。

3 发射载荷下座钣动态响应分析

3.1 全炮有限元建模

迫击炮全炮模型主要包括:座钣,弹丸和炮身(身管、炮尾),炮架(炮箍、双腿架),复合材料座钣置于土壤中,双脚架插入土壤中为身管提供支撑。座钣中的驻臼、底盖、边角等钛合金件结构规整,采用六面体单元划分;座钣复合材料部分采用四边形壳单元划分;土壤采用六面体单元与四面体单元进行划分。全炮网格单元数为220 771,节点数为216 850。迫击炮-土壤耦合非线性有限元模型如图2所示。

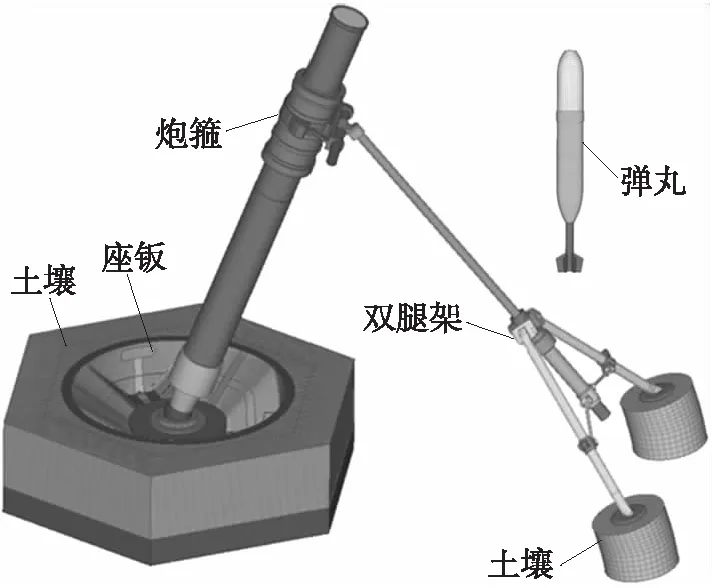
图2 土壤及全炮网格模型

载荷:迫击炮膛底施加膛底压力,弹丸尾部与尾翼中心截面施加弹底压力,重力施加在整个模型上。弹丸与身管内壁之间定义摩擦动接触,座钣外表面与土壤之间定义接触。膛底压力和弹底压力如图3所示。约束:土壤底面固定。

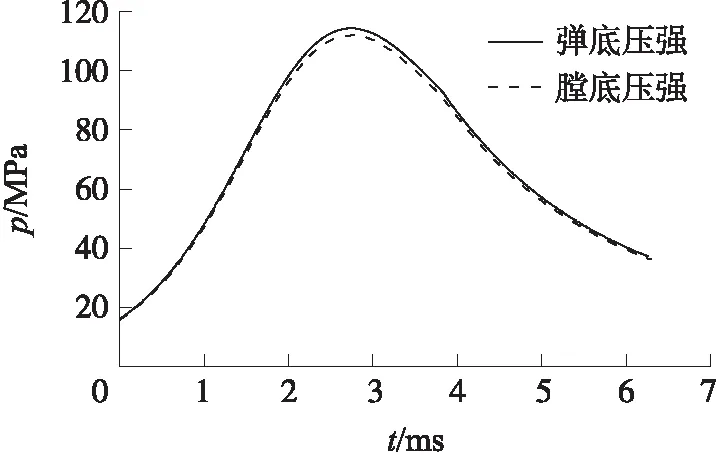
图3 发射载荷-时间曲线

3.2 刚强度仿真结果与分析

迫击炮的高低射角通常在45°～85°之间。本文选择高低角45°,70°和85°作为计算工况,70°为常用高低角。复合材料座钣结构具有三角对称性,可以进行圆周射击,因此选择方向角0°和60°射击工况。

发射阵地的土壤类型有坚硬土、中硬土和软弱土。坚硬土是指水泥地、冻土和密实的碎石土等;中硬土是指中密、稍密的碎石土,密实中砂和坚硬的黄土等;软弱土一般是指淤泥质土、沙土、新近沉积的黏性土和粉土等。发射阵地土壤类型不同,对迫击炮的射击情况及座钣的受力情况有较大的影响。座钣的强度试验一般是在坚硬土上进行。本文选择Drucker-Prager模型来描述土壤的本构关系[9-10],土壤选择属于坚硬土的一种人工填土,3种土壤材料参数如表4所示。

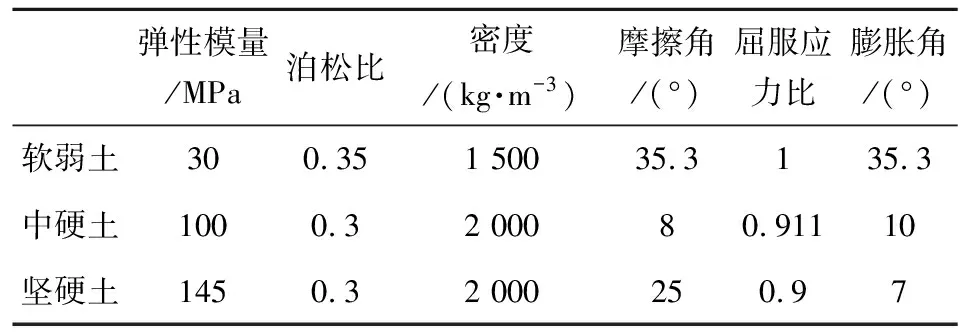
表4 土壤材料参数

进行6种射击工况下的全炮动态非线性有限元仿真,得到迫击炮发射过程座钣在各个时刻的应力和位移分布规律。0°/45°(方向角/高低角)工况下座钣背面的Mises应力云图如图4所示,各工况最大应力和最大位移如表5所示。

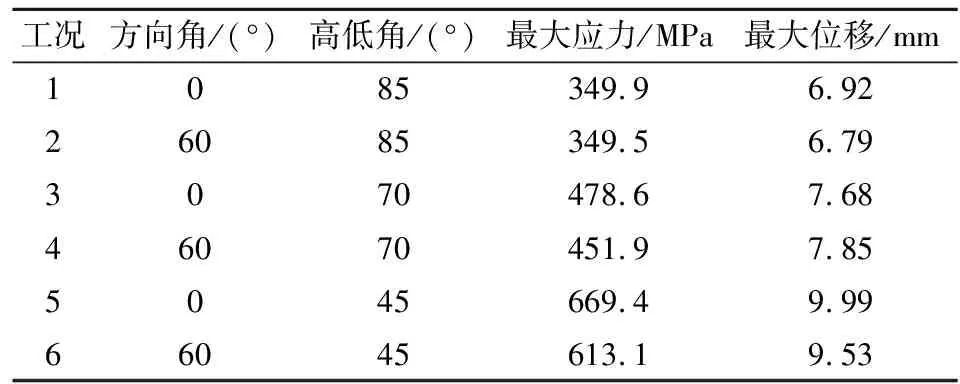
表5 各工况下迫击炮座钣动态有限元数值结果

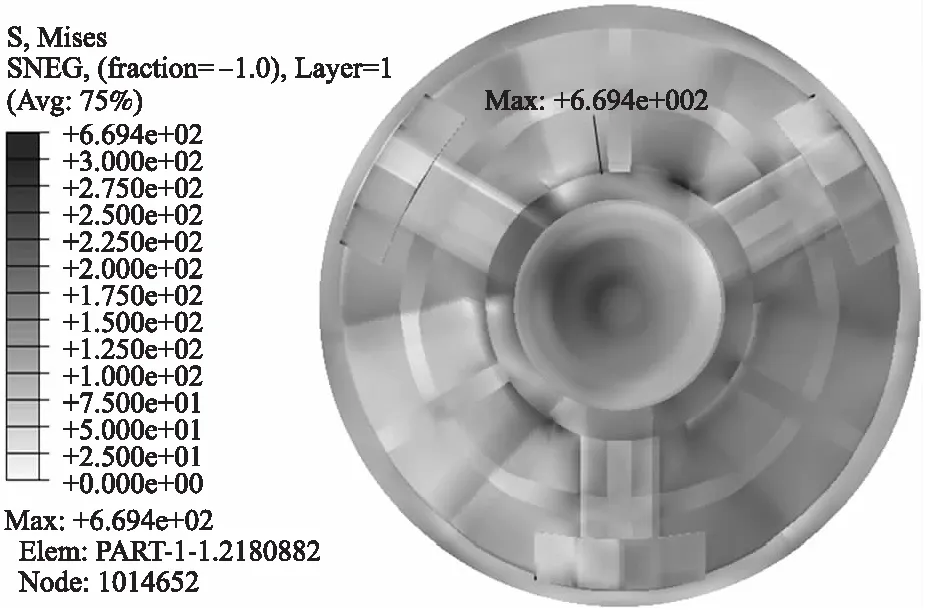
图4 座钣背面应力云图(单位:MPa)

计算结果表明,6种工况中,迫击炮射角为0°/45°时,座钣的最大应力最大,其值为669.4 MPa,位置在炮膛轴线方向、复合材料主体与土壤接触的背面,复合材料座钣结构并未发生失效破坏;方向角分别为0°和60°时,座钣在发射过程中的最大应力和最大位移的值相差较小;当高低角减小时,座钣的最大应力和最大位移会增大,因为炮膛合力在竖直方向的分力会随高低角的减小而减小,其在水平方向的分力会随高低角的减小而增大,水平反向分力增大导致座钣所受的炮膛合力无法均匀地传递至土壤中,使座钣上某些区域产生应力集中。

为了验证仿真模型的正确性,提取座钣在0°/70°工况下,区域A内表面2个相邻节点的x方向正应力σ11(与试验应变片σ11粘贴方向一致)变化曲线,区域A位置如图5所示,应力-时间曲线如图6所示。

图5 区域A位置示意图

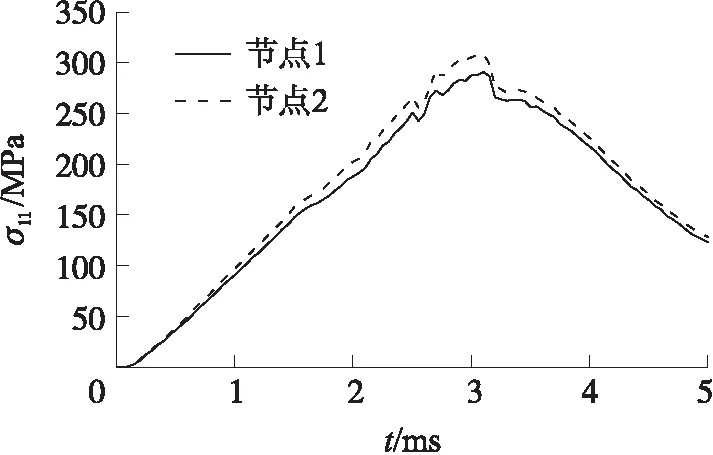
图6 x方向正应力σ11-时间曲线

从图6中可以看出,节点1、节点2的σ11峰值分别为290.9 MPa和308.9 MPa。复合材料座钣样机在射角为0°/70°坚硬土工况下,试验测得区域A在发射过程中σ11最大为281 MPa。节点1和节点2的x轴向应力峰值与试验值的相对误差分别为3.52%和9.93%,相对误差均小于10%,说明复合材料座钣的刚强度仿真结果在一定程度上是可信的。

3.3 炮口扰动分析

迫击炮发射时,不同阵地的土壤类型会使座钣承受不同变化规律的土壤抗力,从而影响迫击炮的炮口扰动。选择迫击炮身管高低射角为70°,方向角为60°,分别选用坚硬土、中硬土和软弱土进行迫击炮发射仿真,土壤的材料属性如表4所示,得到迫击炮发射过程中高低方向的炮口扰动曲线如图7和图8所示。计算结果采用的炮口局部坐标系定义:以炮口中心为原点,以身管轴线为y轴、炮口平面垂直y轴向上为x轴,z轴满足右手定则,弹丸出炮口时刻的炮口扰动值如表6所示。炮口中心沿x轴的位移为纵向位移Ux,沿z轴的位移为横向位移Uz,绕x轴的角位移为水平横向角位移θx,绕z轴转动的角位移为高低角位移θz。

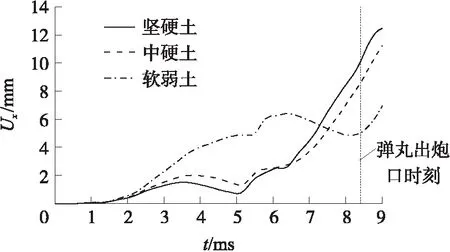
图7 炮口纵向位移

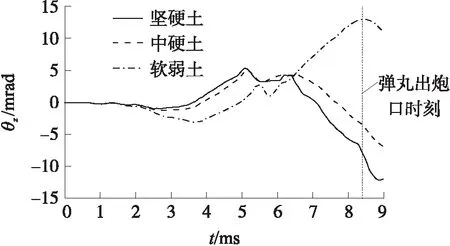
图8 炮口高低角位移

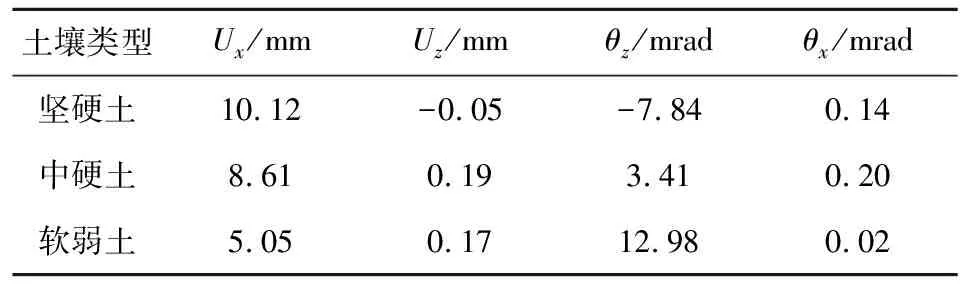
表6 有限元仿真计算结果

从图7、图8和表6中可以看出:①3种土壤类型,炮口的纵向扰动水平均高于横向扰动水平;②在弹丸出炮口之前,坚硬土和中硬土工况下的炮口纵向位移曲线变化趋势相近,且大部分时间内软弱土工况下的炮口纵向位移大于坚硬土和中硬土工况下的炮口纵向位移;③弹丸出炮口时,坚硬土和中硬土工况下的炮口纵向位移及横向位移大于软弱土工况下的纵向位移及横向位移,且坚硬土工况下的炮口纵向位移及横向位移最大;④3种工况中,软弱土工况下出炮口时刻的炮口高低角位移最大,其余2种工况的高低角位移曲线变化趋势相近,且3种工况下炮口横向角位移均较小。这说明不同土壤类型会影响迫击炮射击时的炮口扰动,进而影响迫击炮的射击稳定性。

4 复合材料座钣多目标结构优化

为了使座钣质量和迫击炮在不同土壤工况下射击时的炮口扰动尽可能小,同时又满足复合材料座钣结构的强度要求,对座钣的结构参数进行多工况多目标优化,在重要的结构参数之中寻求最佳组合。

4.1 座钣代理模型建模

神经网络法常用来建立代理模型,因其具备很强的非线性映射能力,一个3层或者3层以上的BP神经网络能够拟合任意复杂的非线性函数。

首先,采用最优拉丁超立方试验设计方法,在设计变量空间中随机安排60组试验样本,设计变量的取值范围如表7所示。表中,t1～t5分别为复合材料座钣的基础厚度、周向筋厚度、纵向筋厚度、底板筋厚度、底板厚度,h为驻臼中心高度。复合材料座钣各铺层区域如图9所示。t1～t5的初值取自原始设计方案,上、下限根据成型工艺和复合材料质量确定。以试验设计样本作为输入,输出为:将60组试验样本代入全炮有限元模型中,计算得到的坚硬土和软弱土工况下的炮口扰动、座钣质量m、最大应力σ。利用神经网络工具箱建立一个5层BP神经网络,利用BP神经网络建立代理模型的流程,如图10所示。

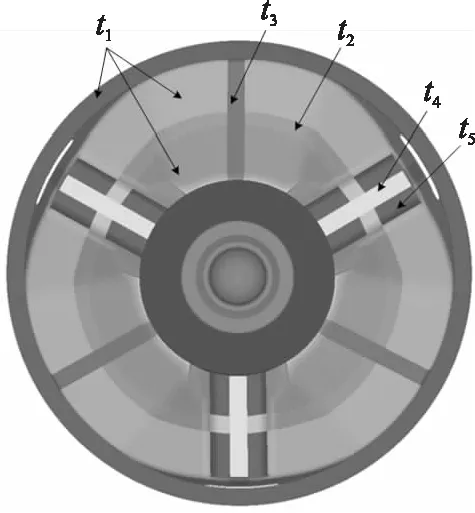
图9 复合材料座钣各铺层区域

表7 设计变量取值范围

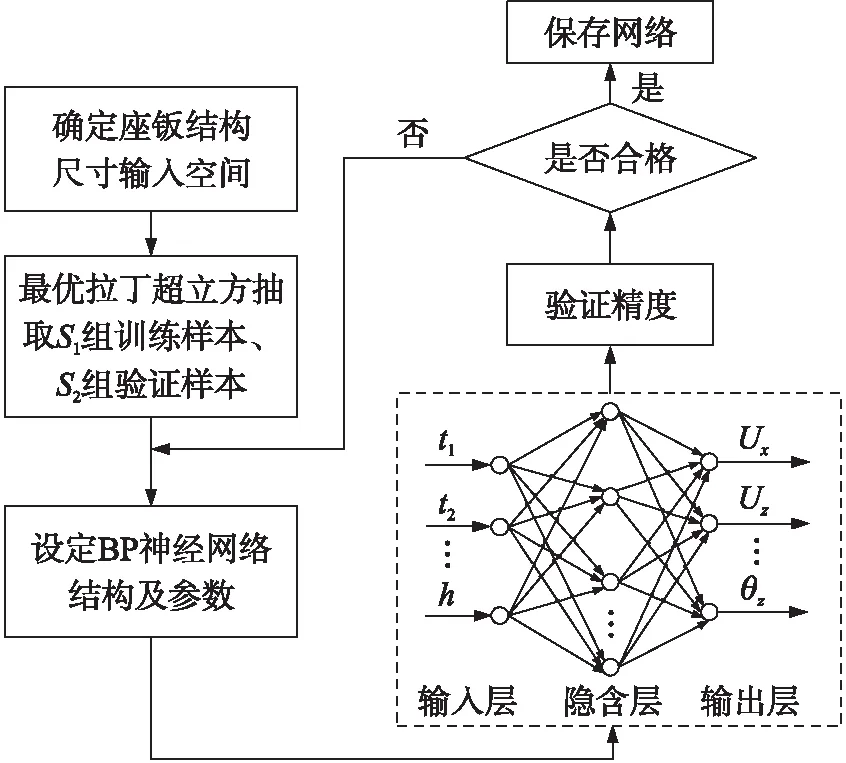
图10 座钣代理模型建模流程

为了验证神经网络的准确性,在设计空间内采用最优拉丁超立方试验设计安排10组验证样本,并代入全炮模型进行计算,土壤类型分别为坚硬土和软弱土,得到炮口扰动、座钣质量及最大应力,以此计算确定性系数R2,用于评价BP神经网络的准确度。

(11)

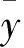
表8 座钣神经网络模型精度检验

4.2 座钣优化模型建模

设计复合材料座钣的目的是为了降低座钣质量,但同时要保证迫击炮的座钣强度要求与炮口扰动较小,故以座钣质量m与弹丸出炮口时的炮口扰动为优化目标,炮口扰动包含了炮口中心参考点的纵向位移Ux、横向位移Uz、高低角位移θz及横向角位移θx这4个特征量。针对这种多目标优化问题,一般将其转换为单目标优化问题,在对4个炮口扰动特征量进行归一化处理后[11],建立的单一工况下的炮口扰动优化目标函数为

(12)

式中:Ux0,Uz0,θz0及θx0为初始条件下弹丸出炮口时的炮口扰动特征量。考虑到坚硬土和软弱土2种工况,则多工况下炮口扰动的优化目标函数为

O=αF1+βF2

(13)

式中:α和β为不同土壤工况下对应的权重系数,若2种工况同样重要,则取α=β=0.5;F1和F2分别为不同土壤工况下对应的炮口扰动优化目标函数。

确定目标函数之后,还需确定设计变量和约束条件。以驻臼中心高度(h)与座钣各区域铺层厚度(t1～t5)为设计变量,座钣最大应力σ<σm(σm=460 MPa)为约束条件,建立优化模型如下:

(14)

式中:n=1,2,…,5。

采用带精英策略的非支配排序的遗传算法NSGA-Ⅱ进行多目标优化,寻找最佳设计点。当达到最大迭代次数时,得到最优参数解集;否则,继续采用NSGA-Ⅱ优化算法求解[12-13]。对初始化种群进行非支配排序,通过遗传算法的选择、交叉、变异生成第一代子代种群;然后,合并父代种群与子代种群,根据非支配关系以及个体的拥挤度选择合适的个体,组成新的父代种群;对新的父代种群进行选择、交叉、变异,然后判断进化代数是否小于最大代数NGen,如果小于最大代数,则继续生成新的父代种群,如果大于最大代数,则终止求解计算,得到最优解集后,将结果代入全炮模型中,求其精确解。

4.3 座钣优化结果及其分析

经过迭代计算,求得的Pareto最优解集如图11所示。通过遗传算法NSGA-Ⅱ多目标优化共得到满足约束条件的最优解25个,从Pareto解集中可以看到,座钣质量m越小, 炮口扰动越大。为了尽量减小炮口扰动,采用图中炮口扰动最小的一组最优解,即Pareto解集中表示优化后质量最大的一点,其对应的设计变量值如表9所示。将设计变量值代入全炮模型进行仿真,得到复合材料座钣在坚硬土工况下的最大应力为455.3 MPa,优化前后炮口扰动对比如图12和图13所示,弹丸出炮口时刻的炮口扰动优化前后结果对比如表10所示。

图11 Pareto解集

表9 优化结果

图12 炮口纵向位移

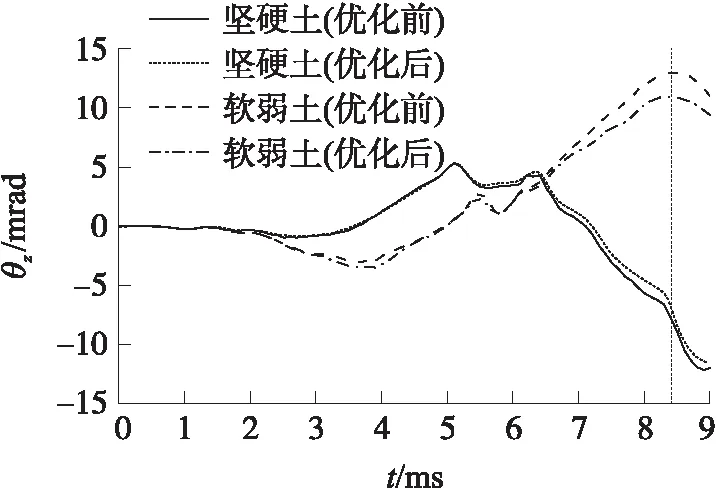
图13 炮口高低角位移

表10 弹丸出炮口时刻的炮口扰动优化前后结果对比

从表10中可以看到,优化后的2种土壤工况下弹丸出炮口时刻的炮口纵向扰动值较优化前减少了至少10%,其中优化后软弱土工况下的炮口纵向位移较优化前下降了26.49%,座钣最大应力为455.3 MPa,满足约束条件。优化后座钣质量为30.77 kg,比初始条件下座钣的质量34.72 kg下降了11.38%。

5 结束语

本文建立了迫击炮座钣与土壤耦合的全炮非线性动态有限元模型,分析了复合材料座钣在不同土壤类型情况下对迫击炮炮口扰动的影响,建立了优化目标为座钣质量与炮口扰动最小的优化模型,采用遗传算法NSGA-Ⅱ进行了多工况多目标优化。相比优化前,优化后座钣的质量与炮口扰动比优化前有明显降低。本文的研究方法和结论可为复合材料座钣的设计与结构优化提供理论参考。