基于准平衡滑翔的再入轨迹解析规划方法
杨 明,刘 明,葛亚杰,杨 丁,曹晶莹
(1.国防科学技术大学 空天科学学院,湖南 长沙 410073;2.空间物理重点实验室,北京 100076)
再入滑翔飞行器具有特殊的高升阻比气动构型,能够在临近空间内长时间、远距离机动飞行,具有速度快、航程远、机动能力强等突出优势,是目前航空航天领域内的研究热点之一[1-3]。而再入滑翔飞行器的弹道规划与制导技术的研究更是当下国内外学者关注的焦点[3-5],本文针对再入滑翔飞行器在多种约束(如受力、热、控制、禁飞区等)条件下的快速轨迹规划问题,研究切合实际工程应用需求的快速轨迹规划技术。
在多约束条件(特别是禁飞区约束)下快速生成再入滑翔飞行器的参考轨迹或者飞行剖面,目前主要有2种途径,即在线轨迹优化技术和轨迹规划技术。轨迹优化技术一般是将上述问题转化为非线性规划问题进行求解。ZHAO等[6]基于分段优化的策略,应用高斯伪谱法解决了航路点和禁飞区等约束条件下的轨迹优化问题。蔺君等[7]采用相同的策略,应用高斯伪谱法实现了多脉冲再入轨迹规划问题。文献[8]利用高斯伪谱法对状态量和控制量进行了离散,将最优控制问题转换为非线性规划问题求解,具有较高的优化效率。文献[9]引入稀疏差分法和网格细化算法,提升了伪谱法的运算效率和精度。但是上述传统的轨迹优化技术在运行效率上还有待进一步的提升,目前尚难以满足再入滑翔飞行器轨迹在线生成的使用需求。近年来,凸优化技术由于其快速收敛特性而被应用到再入滑翔飞行器的轨迹优化问题求解中。LIU等[10]将基于二阶锥规划的凸优化技术应用于再入滑翔飞行器多约束条件下的轨迹优化问题求解。ZHAO等[11]采用分段优化的策略,使用凸优化技术解决了多航路点和多禁飞区等约束条件下的轨迹快速生成问题。WANG等[12-13]使用序列凸优化方法,求解了多约束条件下再入滑翔飞行器跳跃滑翔轨迹的快速生成与跟踪控制问题。然而,凸优化技术及相关制导方法的研究目前仍处于探索阶段,在处理实际问题时,其可靠性等还需要进一步的研究。目前,基于飞行剖面规划的方法是经历过实践验证的且有希望应用于再入滑翔飞行器再入制导环节的典型方法。张科南等[14]研究了再入轨迹与禁飞区位置的几何关系,利用准平衡滑翔条件设计了不同模式的机动再入突防模式弹道。杨丁等[15]利用准平衡滑翔条件推导了高度、速度及航程等关键参数之间的解析关系,给出了一种面向工程应用的纵向平面内再入滑翔飞行器解析轨迹规划方法。赵明等[16]在常值速度倾角和常值阻力加速度的假设条件下,提出了一种纵向平面内解析轨迹规划方法。YU等[17]更是基于解析轨迹规划方法实现了多再入滑翔飞行器在多禁飞区等约束条件下的快速轨迹规划。
综上,本文采用经典的基于飞行剖面的轨迹规划思路,在纵向平面内以准平衡滑翔条件为基础,以剩余航程为自变量,构建高度-航程空间内的多约束飞行走廊;在横向平面内,基于横纵程多次函数的解析规划方法,推导了禁飞区等约束条件下横向剖面的解析形式。上述方法避免了传统优化算法循环迭代计算时间较长且无法保证一定收敛等问题,实现了多约束下再入轨迹快速规划,为再入滑翔飞行器再入轨迹规划和制导提供了新的技术途径。
1 数学描述
1.1 轨迹规划参数定义


图1 轨迹规划再入坐标系
1.2 运动学方程
为了便于轨迹规划算法的研究分析,假设地球为均质圆球且不自转。则再入滑翔飞行器质心动力学方程可表述为
(1)
式中:v为飞行速度,g为重力加速度,γ为速度倾角,ψ为速度偏角,s为航程,r为地心距,Re为地球平均半径,σ为倾侧角,λ为地心经度,φ为地心纬度,aL和aD分别为飞行器的气动升力加速度和阻力加速度。
(2)
式中:ρ为大气密度,Sr为气动参考面积,m为飞行器质量,CL为升力系数,CD为阻力系数,h为飞行高度,χ=1/7 200。
2 基于高度-航程平衡滑翔空间
2.1 基于平衡滑翔的轨迹规划参数解析解

aLcosσ=g-(v2/r)
(3)
基于平衡滑翔条件,根据式(1)中的动力学关系,可得到如下表达式:
(4)
对式(4)积分可得:
(5)
式中:v0为航程计算初始速度,aLcosσ/aD为飞行纵向升阻比。针对确定目标点,当已知滑翔终端航程及终端速度需求时,可将式(5)改写成如下表达式:
(6)
式中:st为滑翔终端航程,vt为滑翔终端速度。根据式(5)和式(6),可得基于平衡滑翔条件下的航程-速度解析关系为
(7)
阻力加速度-航程解析式:


(8)
高度-航程解析式为
(9)
在轨迹规划算法研究中,滑翔飞行器气动力系数一般可近似表示为
(10)
式中:α为飞行攻角;κ0,κ1,κ2为升力系数拟合系数;ζ0,ζ1,ζ2为阻力系数拟合系数。那么,根据以上表达式可得到攻角解析式为
(11)
倾侧角解析式为
(12)
2.2 轨迹规划飞行走廊建立
滑翔飞行器在飞行过程中受到诸多复杂飞行约束条件的限制,下面将首先建立各种约束条件的数学模型,然后再讨论滑翔飞行器飞行走廊的具体形式。
2.2.1 模型建立
①热流约束。
在研究滑翔飞行器轨迹规划问题时,驻点是飞行器加热较严重的区域,因此以驻点热流密度作为约束条件,其表达形式为
(13)
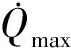
(14)
把式(7)代入,可得h-s空间热流约束边界:
(15)
②动压约束。
考虑到空气舵有效工作范围,给定最大动压约束和最小动压约束,即
(16)
整理得到动压约束边界为
(17)
把式(7)代入可得高度-航程空间动压约束边界:
hq,max(s)≤hq(s)≤hq,min(s)
(18)
③控制约束。
滑翔飞行器依靠空气动力实现对飞行轨迹的控制,为了维持滑翔飞行器的稳定飞行,对滑翔飞行器的攻角取值进行约束:
αmin≤α≤αmax
(19)
根据式(2)可得:
(20)
基于气动模型,并代入式(7),可得高度-航程空间控制约束边界为
hα,min(s)≤hα(s)≤hα,max(s)
(21)
④过载约束。
根据平衡滑翔条件aLcosσ=g-(v2/r),可解算出飞行器滑翔飞行中所受法向过载满足:
(22)
如果令σ≤85°,v≥2 000 m/s,那么由式(22)可得n≤10.7。由于一般滑翔飞行器可承受最大法向过载远大于10.7,所以本文研究过程中暂不考虑过载约束。
2.2.2 规划飞行走廊建立


图2 二维飞行走廊
3 考虑禁飞区规避绕飞的再入轨迹解析规划
再入飞行器飞行过程中需要考虑禁飞区约束,下面针对不同禁飞区约束开展机动弹道规划研究。
3.1 机动绕飞下横向剖面规划基本原理
假设滑翔飞行器在飞行过程中需要绕飞半径为R的禁飞区A(如图3所示),在规划起始点建立规划坐标系Oxyz,飞行器为了避开禁飞区从规划起始点机动飞行至终端T点,初始速度为v0,终端速度为vt,飞行航程为st,对应终端T点飞行纵程和横程为Lstm和Lztm,对应禁飞区中心点飞行纵程和横程为Lsp和Lzp。

图3 单禁飞区绕飞轨迹示意图
根据滑翔飞行器滑翔机动弹道特性,可得飞行纵程与横程和航程之间的关系式为


式中:Ls为纵程,Lz为横程,s为航程,a为横向机动系数。当已知任意目标位置,在规划坐标系下,可根据球面三角形解算得到对应纵、横程:
Lz=Rearcsin(sinφssin(Av-As))
Ls=Rearctan(tanφscos(Av-As))
式中:φs为地心角;Av为规划起始点航向角;λ0和φ0分别为规划起始点地心经、纬度;λ和φ分别为任意点地心经、纬度。
基于图3所示几何关系,可得如下方程组:
(Lstm-Lsp)2+(Lztm-Lzp)2=R2
(23)
(24)
(25)
求解式(23)~式(25),可得到横向机动系数a,根据建立的横程与航程关系,可快速解算得到以航程为自变量的横向机动弹道。
3.2 轨迹规划流程
对于多禁飞区轨迹规划,可转化为多个单禁飞区轨迹规划问题,然后采用3.1节中的横向轨迹规划方法完成多禁飞区轨迹规划。如图4所示,假设飞行器规划起始点是A0,初始速度为v0,目标点是Tm,并有k个禁飞区,假设选取路径为A0→P1→P4→P5→Tm,那么可按如下流程进行轨迹规划(如图4所示)。

图4 轨迹规划流程图
①首先根据禁飞区位置对禁飞区进行编码;
②根据起始点、编码禁飞区和目标点选取路径;
③根据选取路径点,将多禁飞区轨迹规划分段为多段轨迹规划,如图5所示,并针对每分段轨迹完成规划飞行走廊建立;

图5 轨迹规划示意图
④规划段S1:为了规避禁飞区1,飞行器完成机动轨迹AB规划,规划起始点为A0,规划起始速度为v0;
⑤规划段S2:为了规避禁飞区2,飞行器完成机动轨迹BC规划,规划起始点为AB段规划轨迹终点B,规划起始点速度为v1;
⑥规划段S3:为了规避禁飞区k,飞行器完成机动轨迹CD规划,规划起始点为BC段规划轨迹终点C,规划起始点速度为v2;
⑦规划段Sk:为了到达目标点Tm,飞行器完成机动轨迹DTm规划,规划起始点为CD段规划轨迹终点D,规划起始点速度为vk。
4 仿真分析
本文基于CAV-H气动模型开展相关研究。仿真算例规划起始点为再入点,规划结束点为终端点。再入轨迹规划分为再入初段和平衡滑翔段两段进行,再入初段采用定攻角飞行,平衡滑翔段进行多约束下机动轨迹绕飞规划,文中约束主要针对平衡滑翔段轨迹规划。仿真初始参数见表1和表2,约束参数见表3所示。

表1 飞行任务参数

表2 禁飞区参数

表3 约束参数
在给定的初始条件及约束条件下进行仿真分析,仿真分为3个算例,算例1为离线规划(标准状态零偏差),算例2和算例3为考虑飞行器飞行过程中出现偏差情况进行的在线轨迹规划,偏差取值情况见表4所示。
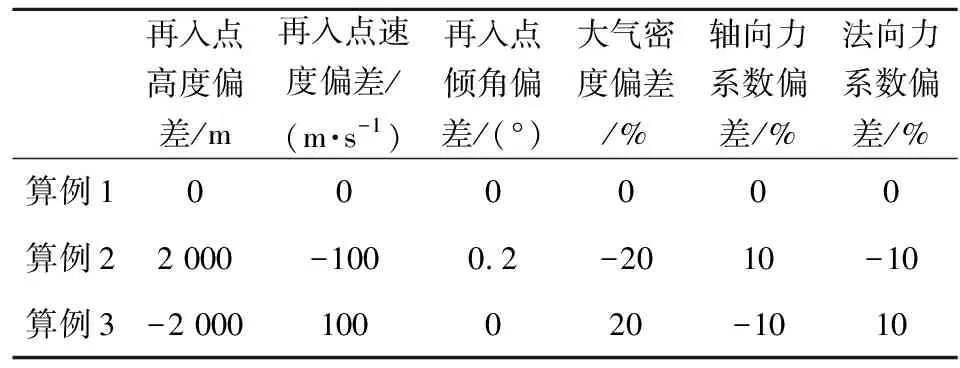
表4 偏差取值
轨迹规划结果参数如表5所示,轨迹规划参数见图6~图13所示。

图6 高度-航程曲线

图7 速度-航程曲线
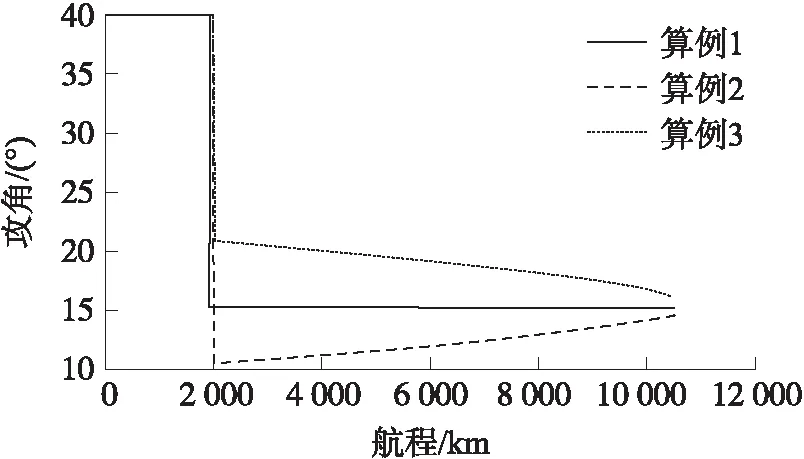
图8 攻角-航程曲线

图9 倾侧角-航程曲线
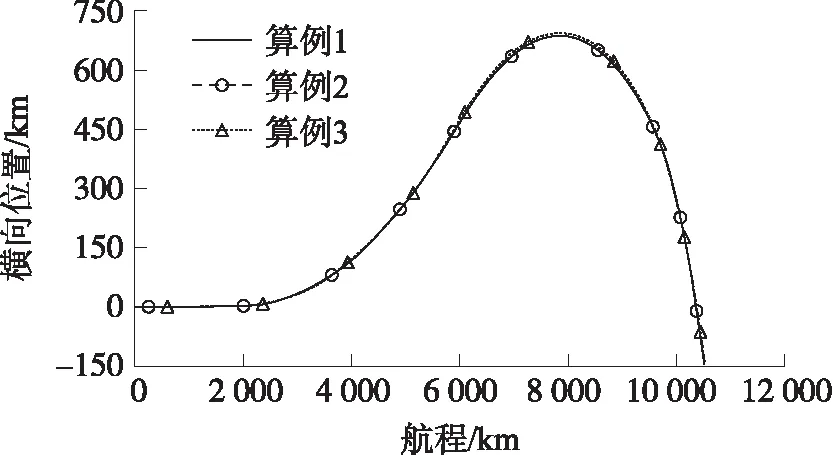
图10 横向位置-航程曲线

图11 纬度-经度曲线

图12 驻点热流-航程曲线
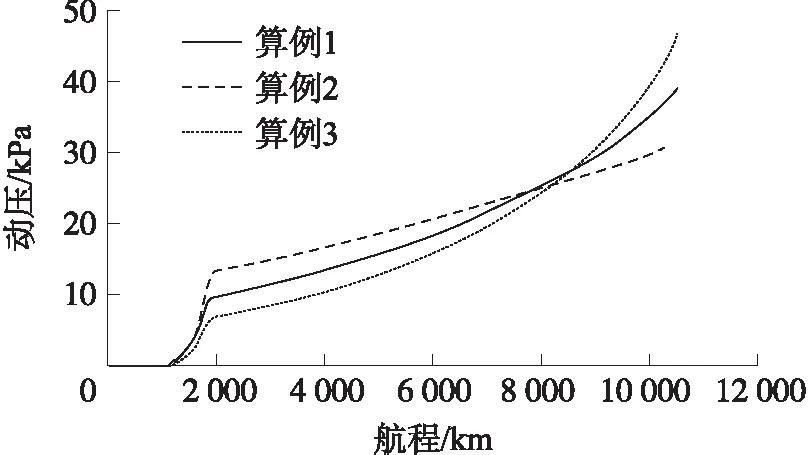
图13 动压-航程曲线
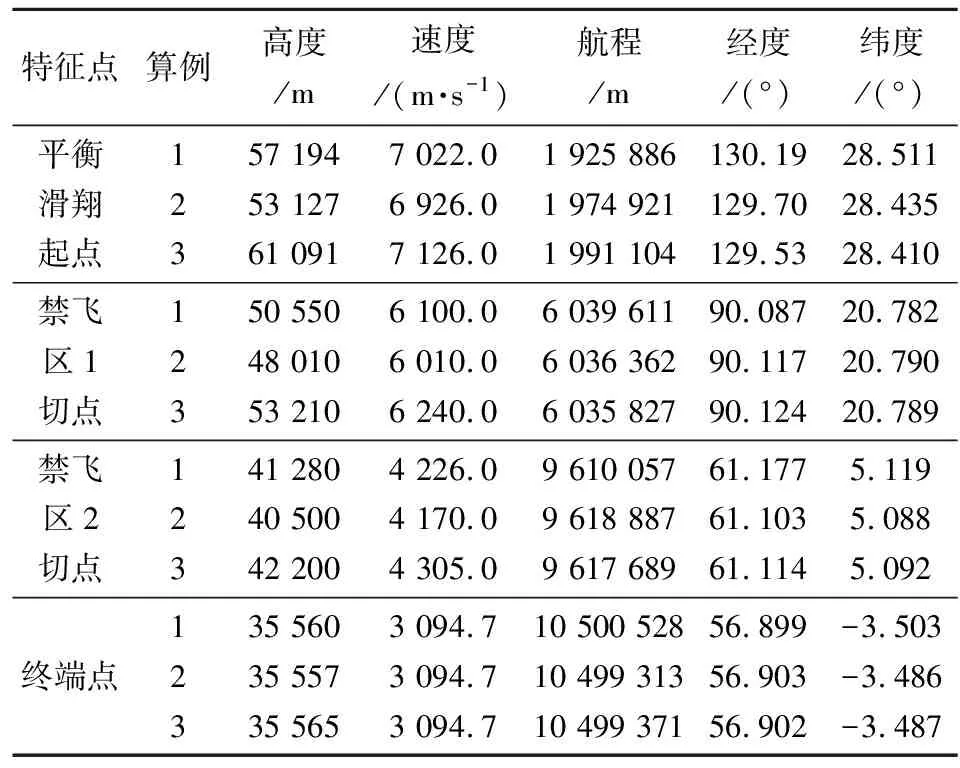
表5 轨迹规划结果
根据仿真分析有如下结论:
①从图6~图7可知,再入点高度、速度和倾角偏差导致平衡滑翔段起始点高度、速度存在差异,但是通过平衡滑翔段轨迹规划,终端点高度、速度均满足要求,终端高度与设计值最大偏差约5 m、速度与设计值最大偏差0、终端位置与设计值最大偏差约1 200 m。规划轨迹高度、速度等参数非常平滑,易于工程实现。
②由图8、图9可知,平衡滑翔段规划攻角范围约10°~22°、倾侧角约为50°,在控制约束范围内,规划攻角和倾侧角较为平滑,易于制导控制跟踪实现。
③由图10~图13可知,平衡滑翔段规划轨迹与禁飞区完全相切,说明本文提出的再入轨迹规划方法实现了对多禁飞区的规避绕飞,满足了禁飞区绕飞要求,且规划轨迹驻点热流和动压均满足约束条件要求。
④本节仿真在计算机系统(操作系统为Windows 7,编译环境为VC++6.0,处理器为Intel core i5-4200H,双核,内存为RAM4.0G,主频为2.8 GHz)上进行,仿真时间约100 ms,采用该方法无须复杂的循坏迭代,计算量小。
5 结束语
本文针对多约束下的再入轨迹规划问题,提出了一种基于准平衡滑翔的再入轨迹规划解析方法,将复杂的多约束轨迹规划问题转化为解析求解,避免了传统优化算法循环迭代计算时间较长和无法保证一定有解等问题,易于工程实现,极大提高了规划速度和可靠性。通过仿真分析可知,本文提出的规划算法运行速度快,规划结果平滑,规划精度较高,规划逻辑简单,为再入滑翔飞行器轨迹在线规划提供了新的技术途径。

