四级渐扩型BLPG内弹道特性实验研究及数值模拟

杨旭光,余永刚

(南京理工大学 能源与动力工程学院,江苏 南京 210094)

在兵器发射与推进技术研究领域,为进一步提高弹丸初速和使用性能,许多新概念、新原理武器应运而生。液体发射药火炮作为其中重要的一类,它是一种以液体发射药为主要燃烧推进能源的新概念武器[1]。与常规固体发射药火炮相比,它具有弹丸初速高、容易实现装填自动化、发射药的爆温低、使用寿命长、战场生存能力强等显著优点[2-3]。

整装式液体发射药火炮是液体发射药火炮中最简单的机械系统,受到了各国学者的广泛关注,但泰勒空腔内燃气在气液交界面上存在相对运动,导致霍姆赫兹不稳定性,这种扰动造成界面上气、液两相混合而使液体发生破碎,正反馈机制导致燃烧不稳定性加剧[4-5],因而其内弹道过程相当复杂,很难控制,研究也因此陷入困境。MORRISON等[6]总结了20世纪80年代以前的研究工作,总体看来研究进展不大。20世纪90年代TALLEY等[7-8]通过大量实验提出,在保证药室容积不变的情况下,采用渐扩型药室结构可有效控制燃烧稳定性。从此,人们对新型药室结构,尤其是渐扩型药室结构展开研究。文献[9-11]先后对各型药室结构条件下,冷态射流在液体工质中的扩展过程进行研究。刘俊[12]对高压环境下含能液体喷射雾化特性及其影响因素进行了讨论。文献[13-15]对BLPG的发射过程和燃烧特性进行分析,并讨论了边界形状对多股燃气射流扩展稳定性的影响。参考BURNETT提出的零维内弹道模型,余永刚等[17]在实验基础上,建立了整装式液体发射药燃烧推进的三阶渐扩型内弹道简化模型,该模型对渐扩型整装式液体发射药火炮的内弹道设计研究具有很好的指导意义。本文设计了一种小口径四级渐扩型整装式液体发射药燃烧推进模拟装置,测得该装置药室内的p-t曲线。在三阶渐扩型内弹道简化模型基础上,构建了一种全新的四级渐扩型整装式液体发射药火炮三阶段内弹道模型,并将实验结果与Visual Basic软件的仿真结果进行对比分析。

1 实验研究

1.1 实验装置

本实验所使用装置主要由点火装置、燃烧室及身管三部分组成。如图1所示,采用在燃烧室本体中嵌入尼龙药室的形式,构造四级渐扩型整装式液体发射药燃烧推进模拟装置的内弹道燃烧室,并且在点火装置、燃烧室及火炮身管三部分的接口处加入垫圈进行密封,以便增加整个实验装置的密封性。

图1 实验装置实物图

该装置的内弹道燃烧推进过程是:先采用电点火,点燃固体点火药,产生高温高压燃气。当达到一定压力后燃气破膜进入储存液体药的燃烧室,引燃装填在燃烧室中靠近底部的液体燃料,这些局部被点燃的燃料所生成的燃气形成泰勒空腔,燃烧即在这个空腔的气液交界面上进行。由于交界面上的燃气存在相对运动,因此导致Kelvin-Helmholtz不稳定性,造成界面上气、液两相混合,从而使液体发生破碎。液体燃料的破碎使气液的接触面积变大,提供了更多的燃烧表面,使燃烧进一步加快进行,泰勒空腔随着燃烧不断变大,最终空腔穿透液柱而追上弹丸。

1.2 实验结果与分析

本实验采用小口径四级渐扩型整装式液体发射药燃烧推进模拟装置,每一级的长度为15 mm,第一级直径为5 mm,以后每级直径递增3 mm,燃烧室总的容积为4.783 cm3。实验采用电点火,在一个密闭容器中放置一个点火药包,药包为硝化棉和2/1固体管状药的混合物,药包中插入电阻丝,点火气流喷射孔直径为2.5 mm。在相同实验条件(装填密度均为0.848 g/cm3)下进行2次实验,利用区截装置采用测平均速度的方法测量弹丸初速,两次测得的数值分别为1 339.1 m/s和1 319.9 m/s。采用江西传感器厂生产的OPT型石英压力传感器测量膛内压力,测得两发药室内的p-t曲线,如图2所示。两发测得的最大膛压分别为227.429 MPa和226.893 MPa。由图2可知:两条曲线的吻合度较高,这表明采用四级渐扩型的液体炮燃烧室可以抑制燃烧过程的不稳定性。

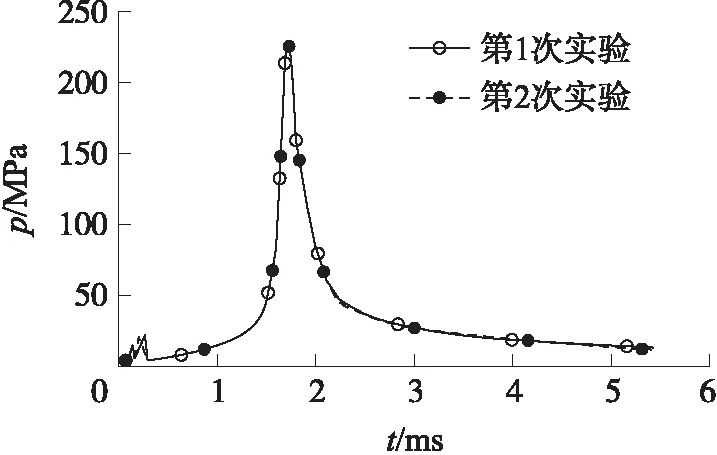
图2 四级渐扩型药室两次实验的p-t曲线

渐扩型药室的台阶能够诱导射流沿径向扩展,促使轴向湍流度降低,部分转向径向湍流度,径向湍流度增大。同时,采用与泰勒空腔发展相适应的四级渐扩型的燃烧室结构尺寸,可以利用阶梯拐角处的卷吸效应与回流有效地减少反应盲区,使燃烧反应区发展平稳。所以,采用本实验设计的四级渐扩型燃烧室结构可以减弱泰勒空腔与赫姆霍兹不稳定效应的正反馈机制,抑制了燃烧反应的随机性,得到一致性较好的p-t曲线。

2 四级渐扩型整装式液体发射药火炮的三阶段内弹道模型

2.1 物理模型

本文采用BURNETT的压力指数公式,结合射流在四级渐扩型药室的扩展过程,并根据小口径BLPG的内弹道特点建立模型。提出以下简化假设:

①由点火射流造成的泰勒空腔初始形状为半球形。液体药燃烧之后,泰勒空腔沿渐扩药室边界呈半球形发展。弹丸启动之后,泰勒空腔呈圆柱形发展。

②液体药燃速公式采用与固体药相似的压力指数形式[18],并引入经验关系式以修正Kelvin-Helmholtz不稳定性对液体药燃烧速率的影响[16]。

③根据Taylor空腔在渐扩药室中扩展以及弹丸运动特点,分3阶段描述弹丸运动规律。即弹丸开始运动之前;弹丸开始运动但泰勒空腔未到达弹底;泰勒空腔抵达弹底但弹丸还未出炮口。其中第2阶段的起始条件为膛内压力≥弹丸启动压力,第3阶段的起始条件可通过药室长度加上弹丸行程与泰勒空腔长度比较获得。

④引入次要功系数来描述身管热损失、燃气动能等能量损耗。

⑤在Taylor空腔的发展过程中,膛内气流速度远远大于液面运动速度,所以假设环形液面的运动速度为0。

2.2 数学模型

根据物理模型中的假设②,可以得到液体发射药的燃速方程为

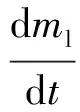
(1)

式中:ml为已燃烧的液体药质量,k为燃速系数,ρl为液体药密度,n为压力指数,p为泰勒空腔的内部压力。

为了反应Kelvin-Helmholtz不稳定性的影响,引入了实际燃烧面积与泰勒空腔几何面积的概念,两者成正比例关系,具体如下:

Aef=fcAc

(2)

式中:Aef为实际燃烧面积,fc为赫姆霍兹不稳定性对燃烧面积的影响系数,Ac为泰勒空腔的几何面积。

影响系数fc可用下式计算[16]:

(3)

式中:C1,C2,C3均为常数;p为压力;Vg为泰勒空腔气相体积。根据假设⑤,设定环形液面的运动速度为0。根据物理模型中的假设③,该内弹道过程可分为3个阶段。根据假设①,Taylor空腔在膛内的发展情况在本文中也进行了描述。

初始Taylor空腔为半球形,因为空腔在弹丸启动之前为半球状发展,当半径增大至与该级渐扩药室半径相同时,半球空腔因受到壁面的限制而呈圆柱状向前扩展,前端仍保持半球状。到达阶梯处则沿阶梯继续扩展半球形前端。空腔到达药室最前端处,圆柱部继续向前扩展,而半球形则变为缺少圆缺的半球形,最终填满整个药室。Taylor空腔在此阶段发展趋势如图3所示。

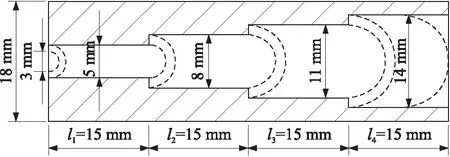
图3 药室内Taylor空腔发展示意图

各阶段的相关方程如下:

①第一阶段,弹丸开始运动之前。

燃气能量方程为

p(Vc-αml)=fml+Ei

(4)

式中:f为火药力。

四级渐扩型药室中泰勒空腔发展方程为

(5)

(6)

式中:vp为弹丸运动速度;Vc为泰勒空腔容积;α为燃气余容;Ei为点火气体的能量,rc为泰勒空腔半径;lc为泰勒空腔长度;l1,l2,l3为前三级各级长度;d1,d2,d3,d4分别为四级渐扩型药室各级直径;V1,V2,V3为前三级各级容积。

②第二阶段,弹丸开始运动,但泰勒空腔未到达弹底。

弹丸运动方程为

(7)

燃气能量方程为

(8)

式中:mp为弹丸的质量,Ap为弹丸的弹底面积,l0为药室相对行程长,lp为弹丸行程,θ为绝热系数,φ为次要功系数。第二阶段四级渐扩型药室中泰勒空腔发展方程同第一阶段,同时根据体积关系可知:

Vc=V-Aplp-Vl

(9)

式中:V为药室总容积,Vl为剩余液体发射药的体积。显然,还存在关系式:

(10)

③第三阶段,泰勒空腔抵达弹底,但弹丸还未出炮口。

弹丸运动方程为

(11)

燃气能量方程为

(12)

四级渐扩型药室中泰勒空腔发展方程为

(13)

3 数值模拟结果分析

将上述式(1)～式(13)联立,Vc为独立未知量,以时间t为自变量,采用四阶龙格-库塔法编程求解。本文模型中所用的基本参数见表1。表中,lg为身管长度;r1,r2,r3,r4分别为四级渐扩型药室各级半径。

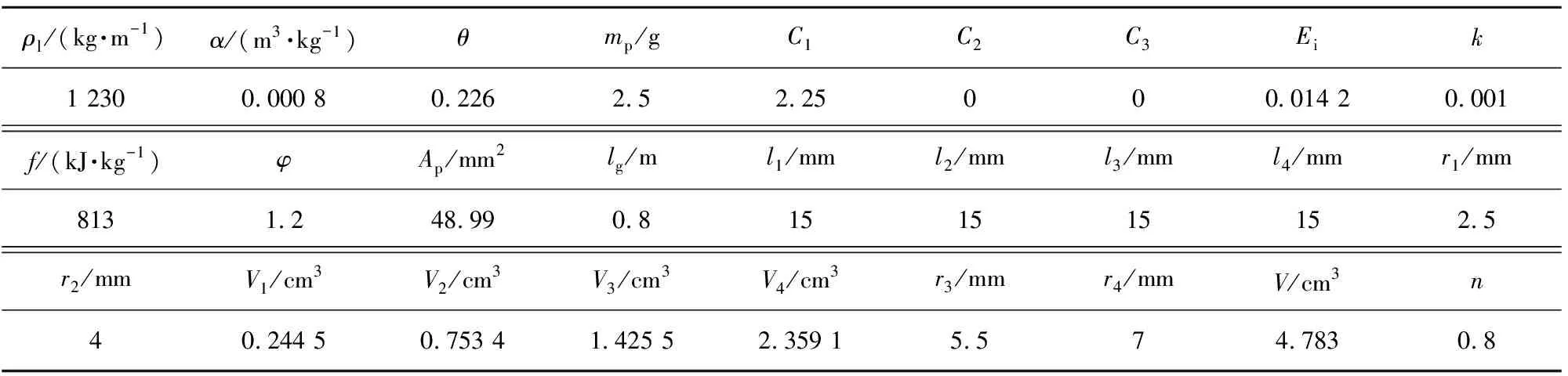
表1 基本参数

内弹道过程的初始条件:泰勒空腔的内部压力为2 MPa,泰勒空腔的直径为3 mm。

针对实验工况进行数值模拟,得到vp-t曲线如图4所示。其中,模拟所得的弹丸初速为1 274.64 m/s,最大膛压为225.52 MPa。

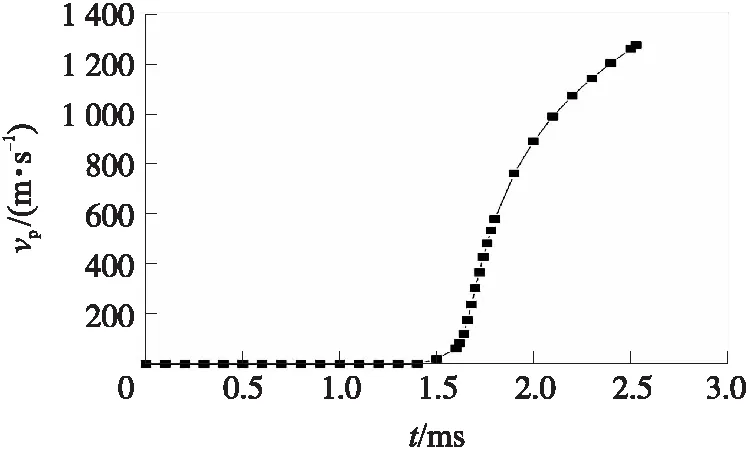
图4 四级渐扩型药室的模拟vp-t图像

选取一条实验测得的p-t曲线,与数值模拟的p-t曲线进行比较,如图5所示。其中模拟值仅计算到弹丸出炮口。

由图5可见,采用本文设计的内弹道模型所得到的模拟计算结果与实验结果较吻合,最大膛压误差为0.8%,弹丸初速的最大误差为5.1%。

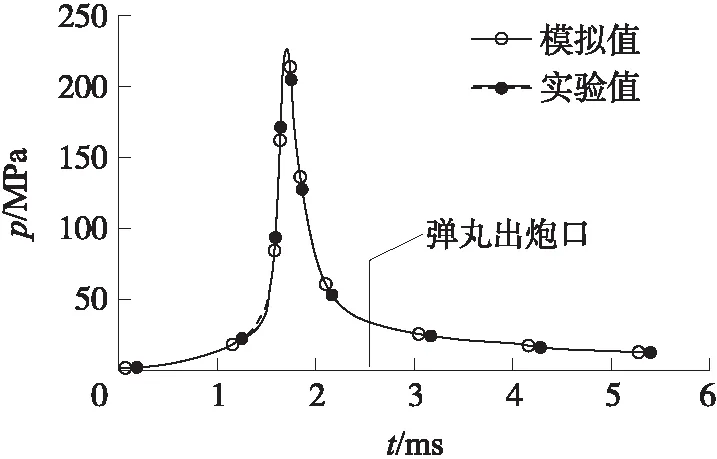
图5 四级渐扩型药室p-t曲线的计算值与实测值对比图像

4 结束语

实验数据及模拟计算结果表明:

①在相同的实验条件下,采用四级渐扩型的燃烧推进模拟装置得到的两发实验结果吻合度较高,说明采用渐扩型的药室结构可以促进燃烧稳定性。

②本文构建了一种四级渐扩型BLPG三阶段内弹道简化模型,其模拟结果与实测结果吻合较好,可用于渐扩型整装式液体发射药火炮内弹道设计研究。