考虑舵机时滞的阵风减缓主动控制律设计

杨阳，杨超，吴志刚，戴玉婷

（北京航空航天大学 航空科学与工程学院，北京100083）

阵风会改变飞机的有效迎角，引起升力的突然变化，从而产生涉及刚性运动和弹性变形的阵风响应［1］。阵风响应会降低飞机的飞行品质，而其所产生的内载荷会影响飞机的疲劳寿命，甚至飞行安全［2］。对于近年来迅速发展的大展弦比柔性飞机而言，其大柔性、低翼载的特点使得阵风响应的影响尤为严重［3］。而阵风减缓主动控制系统能有效降低飞机的阵风响应，保证飞机的飞行安全。

近年来，阵风减缓主动控制技术得到很大程度的发展。杨俊斌等［4］利用经典PID控制减缓飞翼布局飞机的阵风响应，并通过风洞试验进行验证。Liu等［5］利用基于模型预测的线性二次高斯（Linear Quadratic Gaussian，LQG）控制来减缓飞机的阵风载荷。Cook等［6］利用H∞控制来降低飞机的翼根弯矩。Alam等［7］利用具有反馈补偿的前馈控制来减缓飞机的翼根弯矩。Zhao等［8］利用飞机上安装迎角传感器信号采集阵风信息，设计自适应前馈控制器来减缓大型运输机的翼根弯矩。这些控制方法均通过舵机驱动控制面偏转来抑制飞机飞行过程中的阵风响应。动态的控制过程要求舵机具有良好的频响特性。

然而，对于一些小型无人机而言，由于质量、空间及成本的限制，所采用的小型伺服舵机多缺乏频响特性指标。利用所设计的舵机测试平台测试舵机［9］的频响特性，发现此种舵机多存在时滞环节。控制系统的时滞环节会降低系统的阵风响应减缓效果，甚至影响系统的稳定性［10］。因此，在阵风减缓主动控制系统设计过程中必须考虑舵机时滞环节的影响。

目前，针对时滞系统的控制方法通常采用Smith预测控制［11］及相应的改进控制结构。然而此种方法要求一个精确的过程模型，且对受控对象的参数变化敏感。唐功友［12］所设计的时滞系统降维状态预测观测器和控制器也能将时滞项移至系统闭环结构之外，然而要求受控对象可观可控。记忆控制和前馈补偿器 能有效降低时滞和扰动对系统的影响，却需要扰动已知。而Padé近似［14-18］可将时滞环节线性化，得到线性受控对象，并与各种控制系统设计方法相结合设计满足需求的控制系统。

本文将试验所得舵机传递函数中的时滞环节利用Padé近似进行线性化，将线性化后的舵机模型引入气动弹性系统中，利用LQG控制方法［19-21］设计阵风减缓主动控制系统，并利用平衡截断法［22-23］对控制系统进行降阶。利用Simulink将所设计的控制系统引入原非线性模型中进行仿真计算，以验证所设计的阵风减缓主动控制系统的有效性。

1 阵风减缓研究对象

本文的研究对象为一个带有6个后缘舵面及多个传感器的飞翼布局飞机模型（见图1），每个舵面由一个作动器（Hitec-7954SH舵机，该舵机的最大速率为150（°）／s）驱动。取飞机半模进行计算分析，其舵面及传感器编号如图1所示。利用NASTRAN软件对结构有限元模型进行动力学仿真，包括沉浮和俯仰两阶刚体模态及机翼一弯（4.59 Hz）、二弯（16.95 Hz）、一扭（26.42 Hz）及三弯（45.88 Hz）四阶弹性模态，并利用ZAERO计算速度20 m／s、空气密度1.225 kg／m3情况下的非定常气动力，分析此飞行状态下的阵风响应并设计相应的阵风减缓主动控制系统。

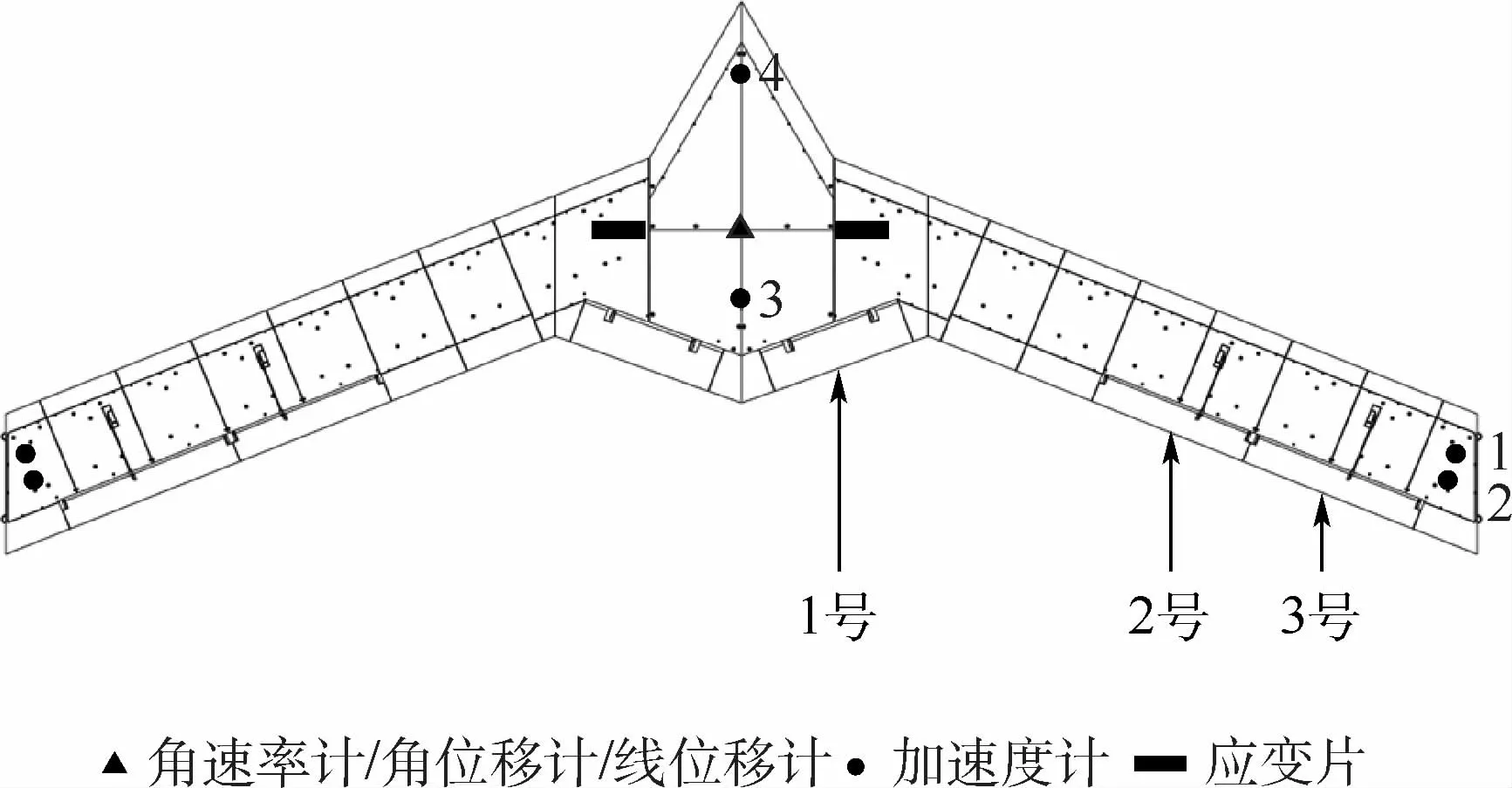
图1 飞翼布局飞机结构模型及传感器舵机布置Fig.1 Structural model of flying-wing aircraft and arrangement of sensors and actuators

2 舵机系统的Padé近似

2.1 舵机的动态特性

利用所设计舵机频响特性测试平台测量模型中所用的伺服舵机Hitec-7954SH带负载（惯性载荷和气动载荷）情况下的动态特性，并根据试验数据利用Levy法［24］对舵机系统进行辨识，得到舵机的传递函数如式（1）所示。舵机的传递函数中存在的时滞环节（e－0.1s）表示舵机的输出信号与输入信号之间存在0.1 s的延迟。

2.2 舵机系统中时滞环节的Padé近似

Padé近似可将时滞环节（e－λs）线性化为一个有理函数连续系统，其近似公式［18］为

根据Padé近似公式，可将舵机的时滞环节拟合成一个高阶传递函数的形式。经过Padé近似线性化后的舵机传递函数为

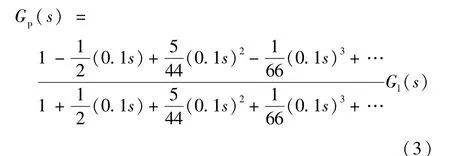
图2为将舵机的时滞环节（e－0.1s）拟合为一个2～6阶传递函数后舵机的阶跃响应和频率响应。由图2（a）所示，时滞环节使得舵机的阶跃响应发生0.1 s的延迟，而经过Padé近似所得线性化舵机模型的阶跃响应在0～0.1 s内存在微小振动，0.1 s之后二者响应保持一致。同时随着Padé近似阶数的升高，其振动的幅值降低，对时滞环节的近似效果更好。

由图2（b）所示，经过Padé近似线性化后系统的幅频特性与包含时滞环节的舵机系统相一致，即Padé近似并不会改变系统的幅频特性。同时，Padé近似能有效近似时滞环节所引起的相位滞后，但不同的近似阶数影响着一定频率范围内的近似精度。对于图1中所示飞翼布局飞机模型而言，阵风主要影响飞机的短周期模态（1.23 Hz）和机翼一弯模态（4.59 Hz）。由图2（b）可知，4阶以上的Padé近似所得线性系统的相频特性在0～10 Hz频率范围与时滞系统保持较好的一致性，而此频率范围满足阵风减缓主动控制系统的设计需求。因此，在满足阵风减缓主动控制系统设计频响需求的基础上，为了保证所建立受控对象的阶数不会过高，本文选用4阶Padé近似所得到的传递函数代替舵机中的时滞环节，建立线性化舵机模型，进行阵风减缓主动控制系统设计。

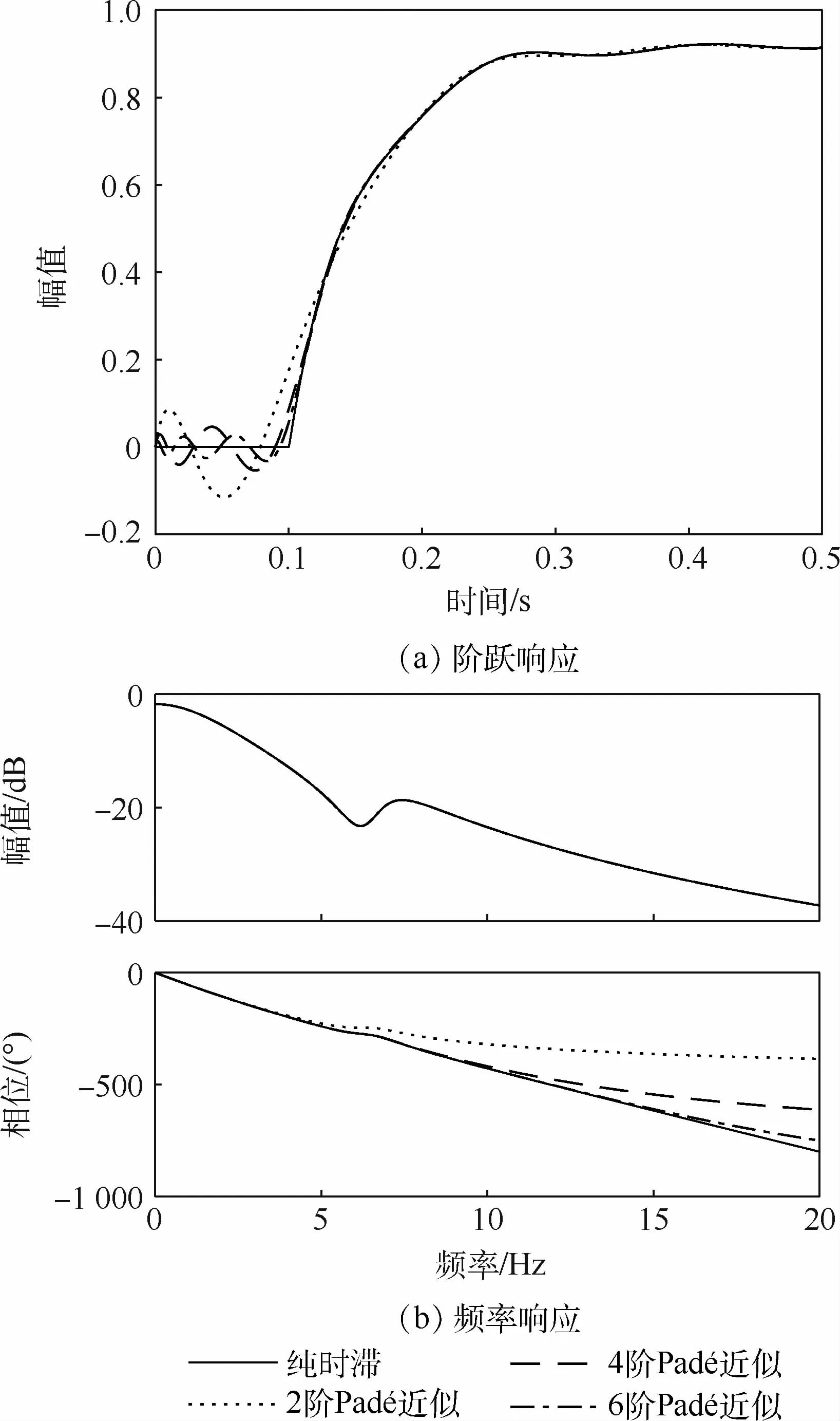
图2 包含纯时滞模型及2～6阶Padé近似模型的舵机阶跃和频率响应Fig.2 Step and frequency responses of actuator with pure time-delay model and 2～6 order Padé approximation models

3 气动伺服弹性系统建模流程

3.1 气动弹性系统建模

式中：xae为气动弹性系统的状态向量；δae为舵面偏转输入向量；wae为阵风扰动输入向量；yae为气动弹性系统的输出向量；Aae、Bae、Cae、Dae、Eae和Fae分别为气动弹性系统的状态矩阵、舵机输入矩阵、阵风输入矩阵、输出矩阵、舵机前馈矩阵和阵风前馈矩阵。对于图1所示飞翼布局飞机其输出向量包括翼尖加速度（1号和2号）、机身加速度（3号和4号）、位移、角速率和角位移信号。

3.2 舵机系统建模

根据式（3）可以得到舵机系统的状态空间方程。单个舵机的状态空间方程如下：

3.3 增稳控制系统建模

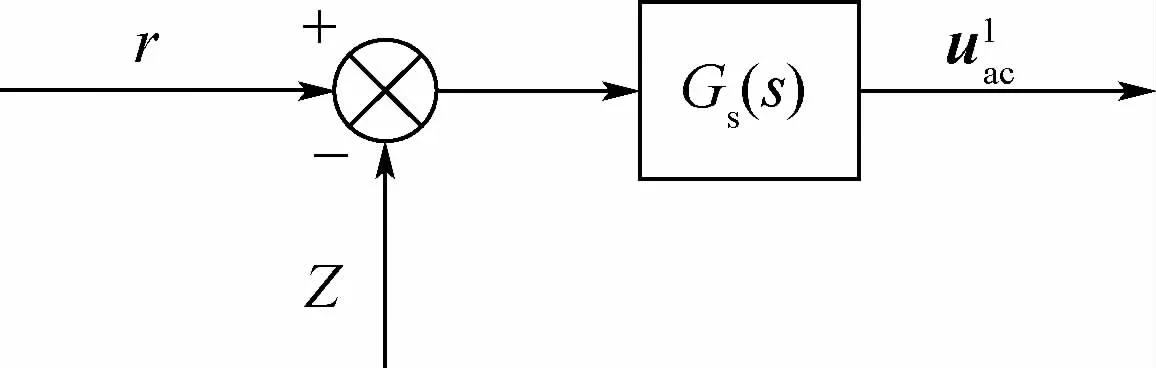
图3 增稳控制系统结构Fig.3 Stability augment control system

3.4 气动伺服弹性系统建模

4 阵风减缓主动控制系统设计

利用LQG控制方法［14-15］对式（11）所示气动伺服弹性模型设计阵风减缓主动控制系统，其由Kalman状态估计观测器和状态反馈控制器2个部分组成［21］。Kalman状态估计观测器根据传感器所测系统输出估计气动伺服弹性系统的状态，估计的状态量经过所设计的状态反馈控制器生成控制信号，驱动2号舵面和3号舵面进行偏转。

所设计的阵风减缓主动控制系统如图4所示。其中Kalman状态估计观测器的参数KK和阵风减缓最优控制器反馈参数KL可通过求解黎卡提方程［14-15］获得。在控制器反馈参数的设计过程中选取合适的输出输入加权矩阵，以达到阵风响应减缓效果。

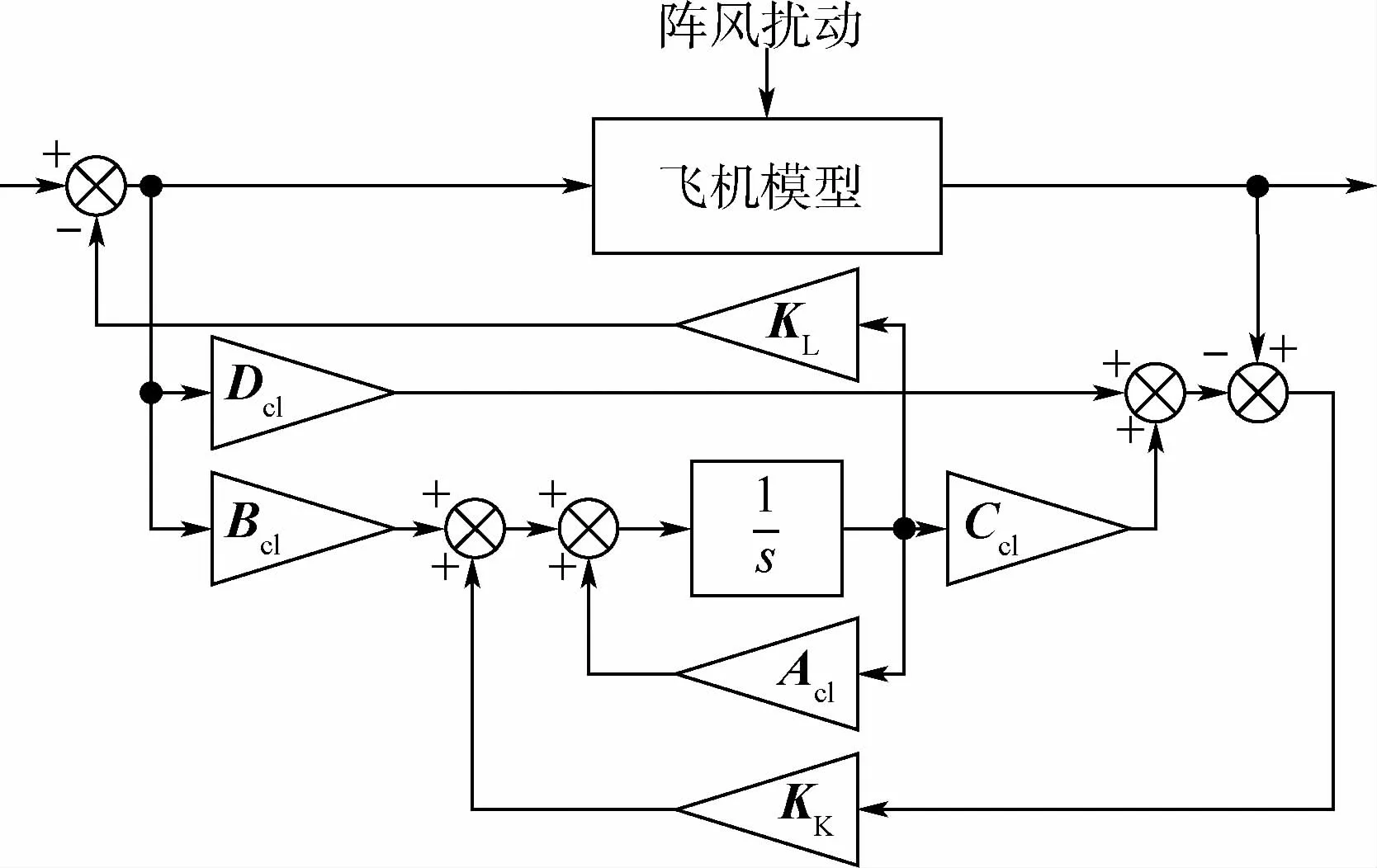
图4 阵风减缓主动控制系统Fig.4 Gust alleviation active control system

对图1所示飞翼布局飞机而言，其输出为翼尖加速度（1号和2号）、机身加速度（3号和4号）、位移、角速率和角位移信号，输入为2号和3号舵面的舵机输入信号。而所设计的阵风减缓主动控制系统目的为减缓飞机机身处的过载和翼根弯矩，同时保证整个控制过程中，舵面的偏角不大于舵机的可用偏角，即±20°，以及舵机的偏转速率不大于150（°）／s，因此选取输入和输出的加权矩阵为

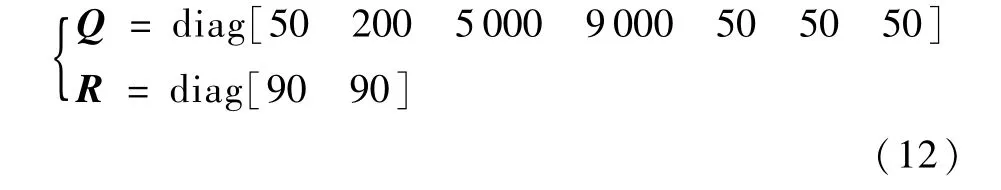
然而，基于LQG控制方法所设计的阵风减缓主动控制系统会与受控对象保持相同的阶数。对于气动伺服弹性系统而言，阶数往往较高，较高的控制律不利于物理实现。因此，采用平衡截断法对所设计的阵风减缓主动控制律进行降阶（14阶）。

5 阵风减缓主动控制系统仿真分析

5.1 阵风减缓主动控制仿真

利用Simulink将第4节中所设计的经过降阶的控制系统引入到包含时滞环节的气动伺服弹性模型中进行仿真，分别计算开环和闭环情况下模型在von Karman连续阵风（阵风速度均方根为1 m／s，阵风尺度为760 m）激励下的响应，并根据力的叠加法计算图1所示应变片位置的翼根弯矩响应，从而验证根据线性化气动伺服弹性模型所设计的阵风减缓主动控制方案对于非线性模型的有效性。其仿真模型如图5所示，包括气动伺服弹性模型、增稳控制系统、阵风减缓主动控制系统及阵风成型滤波器。其中，阵风成型滤波器将输入的高斯白噪声生成与von Karman功率谱密度相吻合的时域连续阵风［26］。图6为包含时滞环节的舵机仿真模型。

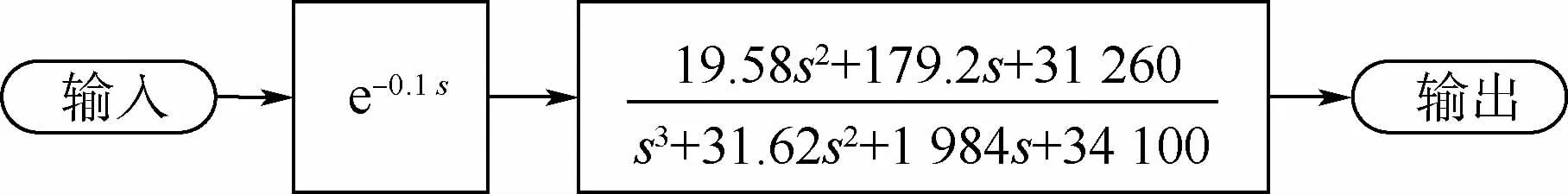
图6 舵机的仿真模型Fig.6 Simulation model of actuator

5.2 阵风减缓效果分析

根据式（2）将舵机的延迟后环节近似化为一个4阶的传递函数，构建式（11）所示的气动伺服弹性系统模型，并采用式（12）所示的加权矩阵利用LQG控制方法设计阵风减缓主动控制系统，并将所设计的控制系统进行降阶，计算3号、4号加速度计处的过载和翼根处的弯矩，如图7所示。并计算开／闭环状态下阵风响应的均方根值，如表1所示。

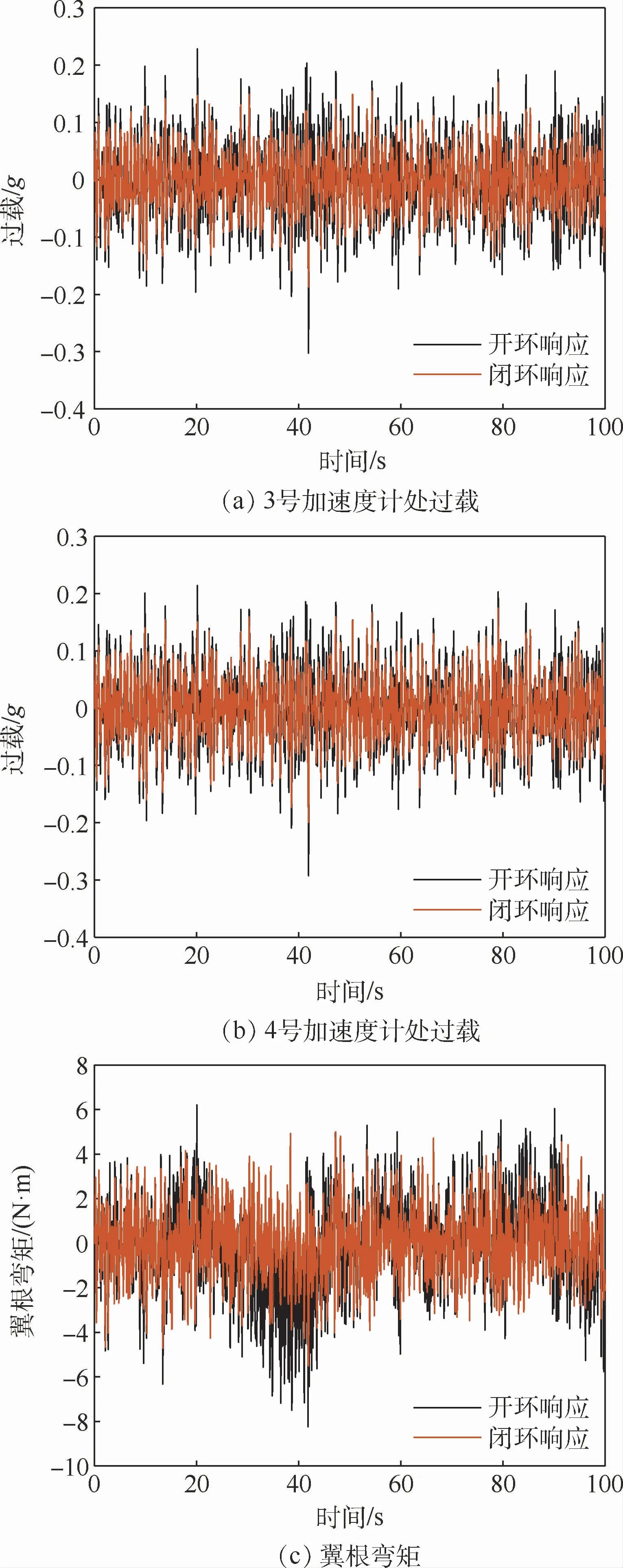
图7 气动伺服弹性模型的阵风响应Fig.7 Gust responses of aeroservoelastic model

如图7所示，所设计的阵风减缓主动控制系统可以有效减缓机身加速度计处的过载响应，减缓效率均在15%左右，而对于翼根弯矩具有较好的减缓效果，效果达到25%以上。

表2中列出了所设计的阵风减缓主动控制系统对Padé近似化后的线性气动伺服弹性系统和包含时滞环节的非线性气动伺服弹性系统的阵风减缓情况。2种情况下的阵风减缓主动控制效果基本相同且所设计的阵风减缓主动控制系统对线性模型的减缓效果略大于非线性模型，说明Padé近似能有效模拟舵机中的时滞环节，并且所得结果较非线性模型而言并不保守。

由此可见，利用Padé近似将舵机中所存在的非线性时滞环节进行线性化，根据线性模型所设计的阵风减缓主动控制系统能有效减缓原模型的阵风响应。

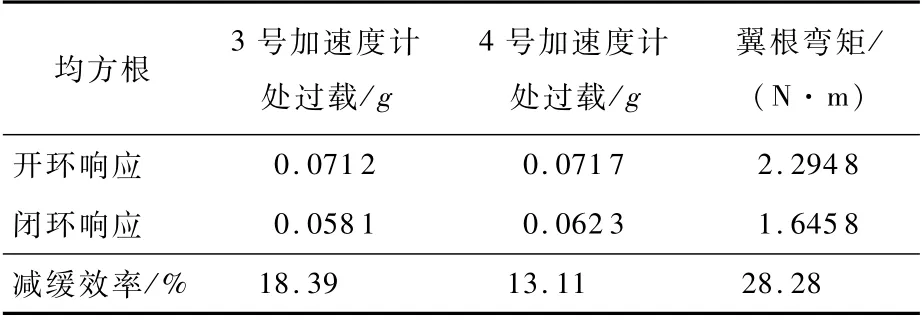
表1 阵风响应的均方根及减缓效果Tab1e 1 Root-mean-square of gust responses and effects of gust a11eviation

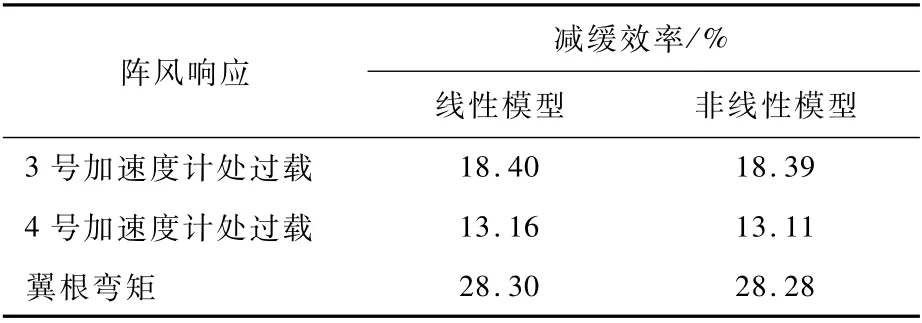
表2 线性模型和非线性模型的阵风减缓效果Tab1e 2 Gust a11eviation effects of 1inear mode1and non1inear mode1

5.3 Padé近似阶数对阵风减缓效果的影响

选取不同的Padé近似阶数替代舵机中的时滞环节，进行LQG阵风减缓主动控制系统设计。所设计的控制系统对包含时滞环节的气动伺服弹性系统的阵风响应减缓效率如表3所示。

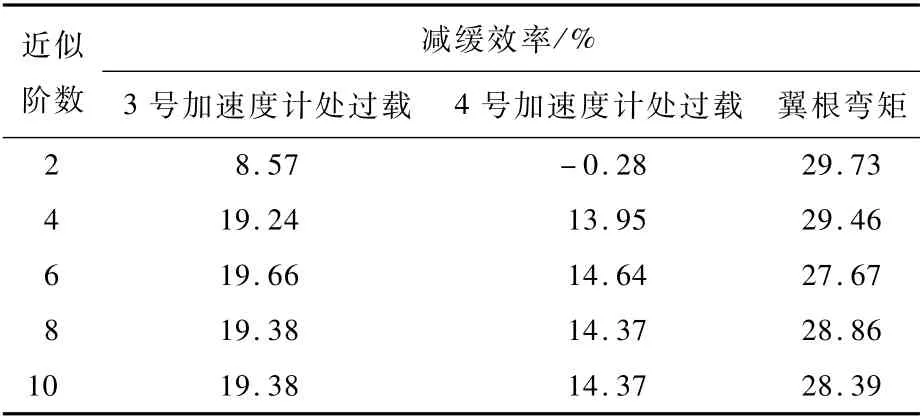
表3 不同Padé近似阶数下所设计控制系统的阵风减缓效果Tab1e 3 Gust a11eviation effects of designed contro1 svstem based on different Padéapproximation orders

如图2所示，过低的Padé近似阶数（2阶）无法在主要气动弹性振动频率范围内准确描述舵机中所存在的时滞环节，从而影响所建立的线性受控对象的准确性，进而导致所设计的控制系统对于包含时滞环节控制对象的作用效果并不明显，甚至会加剧某些响应。同时，较高阶（4～10阶）的Padé近似保证所建立的线性模型在主要气动弹性振动频率范围内与原时滞模型的频响特性具有较好的一致性，从而保证所设计的阵风减缓主动控制系统均能较好地减缓原气动伺服弹性模型的阵风响应，且其减缓效果相差并不大。因此，在满足阵风减缓主动控制系统设计需求的条件下，为了降低所建立受控对象的阶数，从而降低所设计控制系统的阶数，建议选取较低的Padé近似阶数进行控制系统设计。

5.4 控制律降阶对阵风减缓效果的影响

采用LQG控制方法所设计的阵风减缓主动控制系统具有较高的阶数，对于5.1节中所述气动伺服弹性模型而言，在选取4阶Padé近似的情况下，控制系统高达44阶，物理实现较为困难。因此采用平衡截断法对所设计的控制方案进行降阶。

对比控制系统降阶前后的频率响应，选取输入为俯仰角扰动、输出为Flap2舵机控制信号和输入为位移扰动、输出为Flap3舵机控制信号的传递函数绘制Bode图，如图8所示。在高于14阶的情况下，在重要的弹性频率范围（0～10 Hz）内，降阶系统与满阶系统具有较好的一致性，而在低于14阶的情况下，降阶后系统的幅值和相位与满阶系统相差较大。因而，对于本文所设计的控制系统，可利用平衡截断法将高阶的控制律降低到14阶。

表4列出了4阶Padé近似的情况下不同阶数控制系统对阵风响应的减缓效果。由此可见，控制律的降阶会导致所设计控制系统的效果降低，即导致阵风减缓效率降低。在控制律小于14阶的情况下，由于降阶后控制系统与原系统的频响特性相差较大，从而导致系统失稳，即机身加速度计（3号和4号）处的过载及翼根弯矩均产生发散。因此，在阵风减缓主动控制系统设计过程中需要选择合适的降阶阶数，在保证系统稳定和减缓效果的基础上，选取较低的降阶阶数。

表5和表6列出了6阶和8阶Padé近似情况下，控制律降阶对阵风减缓控制系统的影响。对比表4～表6可知，在不同的Padé近似阶数情况下，降阶均会降低所设计控制系统的阵风减缓控制效果。而对本文所设计的控制系统而言，在选用较高阶Padé近似的情况下，未在控制系统降至12阶时出现如表4所示的系统失稳，但其对翼根过载的减缓效果出现了明显的下降。由此可见，Padé近似阶数对控制系统的降阶存在影响。对本文所述模型而言，选用4阶Padé近似在保证阵风减缓效果的条件下，使得降阶后所得控制律的阶数（14阶）小于6阶和8阶Padé近似的情况（16阶）。

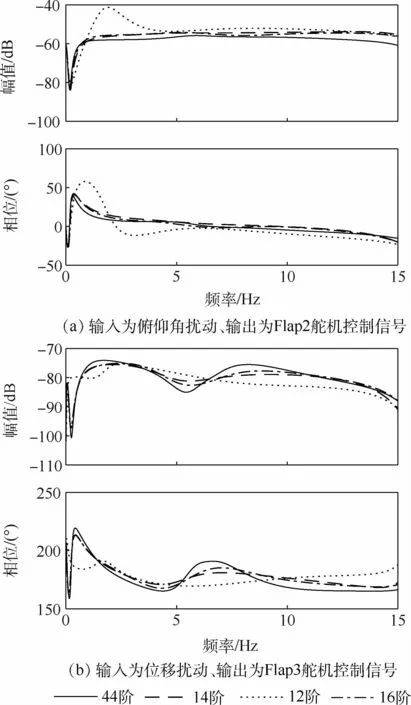
图8 降阶前后控制系统的频率响应Fig.8 Frequency responses of control system before and after order reduction

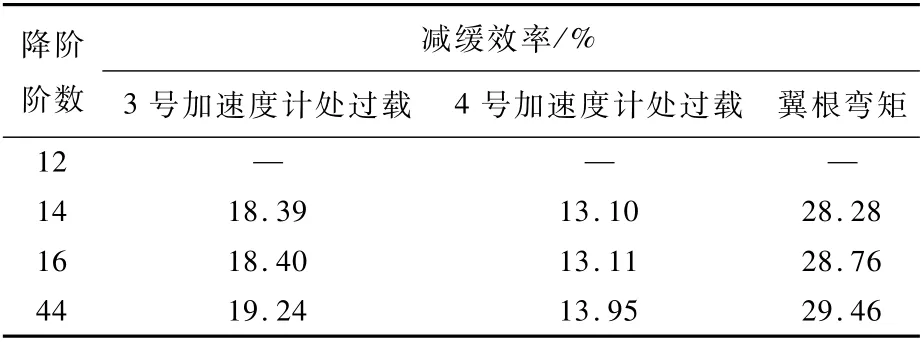
表4 控制律降阶对阵风减缓效果的影响Tab1e 4 Effect of order-reduction on gust a11eviation

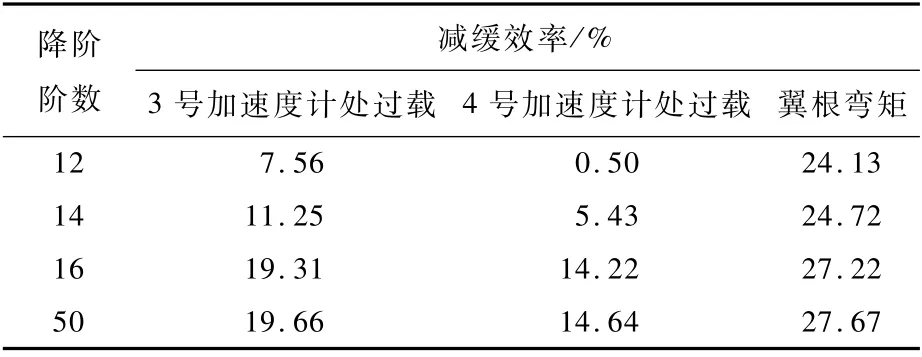
表5 6阶Padé近似情况下控制律降阶对阵风减缓效果的影响Tab1e 5 Effect of order-reduction on gust a11eviation in case of 6-order Padéapproximation

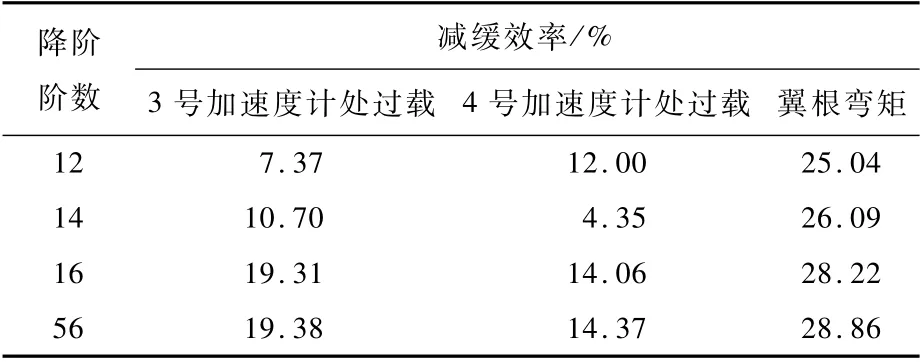
表6 8阶Padé近似情况下控制律降阶对阵风减缓效果的影响Tab1e 6 Effect of order-r eduction on gust a11eviation in case of 8-order Padéapproximation

5.5 阵风减缓主动控制系统鲁棒性分析

采用闭环回差矩阵的最小奇异值方法［27］对降阶前／后所设计的阵风减缓主动控制系统进行鲁棒性分析，如图9所示。控制律降阶会影响低频处的最小奇异值，但在高频部分二者基本保持一致。

在全频率范围内，降阶前系统的最小奇异值为0.309，降阶后系统的最小奇异值为0.389。若取σM＝0.3为系统鲁棒性性能约束，则所设计的阵风减缓主动控制系统在全频率段均具有较好的鲁棒性，且降阶并不会导致系统的鲁棒性变差。

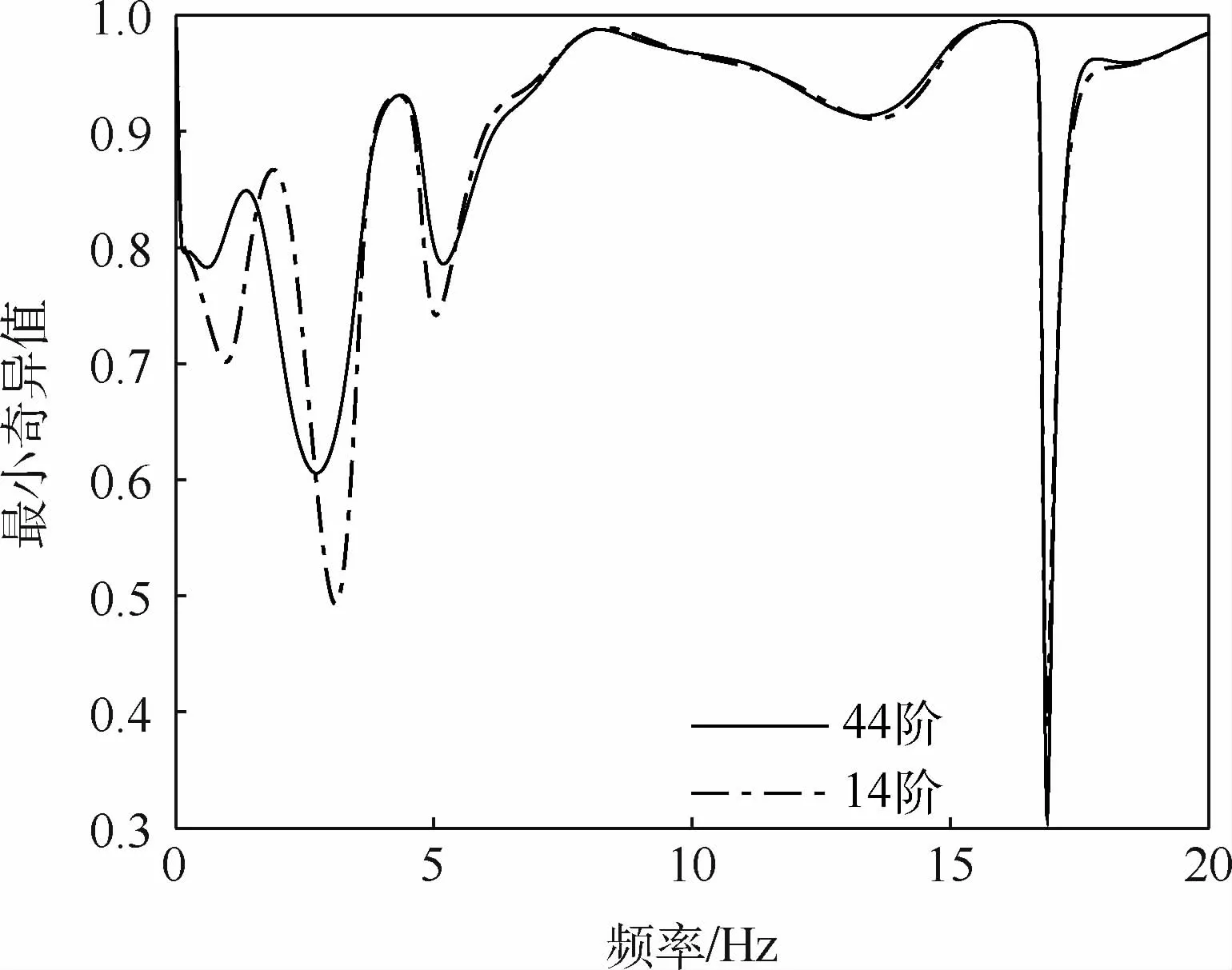
图9 降阶前后系统回差矩阵的最小奇异值Fig.9 Minimum singular value of closed-loop system before and after order reduction

6 结 论

将基于舵机时滞环节线性化后得到的气动伺服弹性系统利用线性二次高斯控制方法所设计的阵风减缓主动控制律引入原包含舵机时滞环节的非线性气动伺服弹性系统中进行仿真计算，计算结果表明：

1）所设计的阵风减缓主动控制系统能有效减缓包含时滞环节的气动伺服弹性模型的阵风响应（机身过载和翼根弯矩）。

2）Padé近似阶数对阵风减缓主动控制系统的设计存在影响。较低的近似阶数无法准确描述时滞环节在高频处所产生的相位滞后，从而导致所设计的控制系统对包含时滞环节受控对象的阵风响应减缓效果不明显，甚至可能加剧某些响应。因此，在控制系统设计过程中，所选择的Padé近似阶数需要保证线性化模型的频响特性在主要的气动弹性频率范围内与原模型保持较好的一致性。在此基础上选取较低的近似阶数保证所建立的受控对象及所设计的控制系统的阶数不会过高。

3）控制律降阶会导致所设计的控制系统效果下降，甚至可能造成系统失稳。通过对比控制系统降阶前后的频响特性，选择合适的降阶阶数，使得降阶前后控制系统在重要的气动弹性频率范围内保持较好的一致性，从而保证降阶后阵风减缓主动控制系统仍有良好的控制效果。