极稀疏投影数据的CT图像重建
武丽君,孙丰荣,杨江飞,于倩蕾,贺芳芳
(1.山东大学 信息科学与工程学院,青岛266237; 2.山东大学 微电子学院,济南250101;3.山东大学附属山东省立医院 医学影像科,济南250014)
传统计算机断层成像(CT)机在螺旋扫描情况下旋转一周一般需要投影1 000~2 000次[1-2]。已有研究显示,CT检查的X-射线辐射可增加病人患癌症的风险[3-4],过量的X-射线辐射还会对人体产生不可逆的辐射损害如染色体变异等[5-6]。临床上,可以通过减少投影角度数来降低X-射线对人体的伤害。减少投影角度数也能够缩短扫描时间从而改善动态器官的成像效果。因此,研究如何在稀疏投影数据情况下进行CT图像重建具有重要的临床意义。
针对不完全投影数据的CT图像重建算法可以分为2类:第1类只适用于特定的扫描结构,首先将不完整的投影数据进行插值补充完整,然后再采用滤波反投影(Filtered Back-Projection,FBP)算法进行图像重建;第2类是迭代类的CT图像重建算法,如代数重建技术(Algebraic Reconstruction Technique,ART),但传统迭代类算法的计算时间要求高,在早期CT中没有得到应用。近年来,随着大规模并行计算技术的发展以及计算机硬件成本的降低,迭代类算法已经成为相关领域研究人员和CT机生产厂商高度关注的热点。这其中较典型的是Sidky等在2006年提出的TV(Total Variation)算法[7-8],该算法利用梯度图像稀疏性先验知识提高了稀疏投影条件下的重建图像质量。TV算法具有很高的实用性,但是TV算法的图像平滑效应会降低图像的空间分辨率和对比度。TV算法是一种启发式的最优化计算方法,压缩感知(Compressed Sensing,CS)理论[9]在一定程度上为TV算法良好的应用性能提供理论支撑。随后又出现诸多基于CS理论的CT迭代图像重建算法,较知名的是美国威斯康辛大学Chen博士及其研究组利用动态CT图像序列相关性先验知识提出的先验图像约束压缩感知(Prior Image Constrained Compressed Sensing,PICCS)算法 。PICCS算法要求能够从冗余或完整的投影数据集合中选取均匀采样的投影数据并利用解析的FBP算法获得所谓的先验图像,这极大地限制了该算法的应用范围;同时,当先验图像和待重建图像不完全对应时,由该算法得到的重建图像会出现伪影。随后,Debatin等[11-12]将各向异性全变差作为目标函数进行CT迭代图像重建,提出了ATV(Anisotropic Total Variation minimization)算 法 和GATV(Generalized Anisotropic Total Variation minimization)算法,在稀疏投影数据的情况下,ATV算法和GATV算法较经典的TV算法得到的重建图像边界更清晰、细节更丰富。
综合已有文献并与CT工程技术人员进行交流,将[0,2π)范围内扇束/锥束扫描不超过20个投影角度称为极稀疏投影,并着力于从极稀疏投影数据足够精确地重建断层图像,从而能够在显著降低CT检查X-射线辐射剂量的前提下,提供充分适宜影像学临床诊断需求的重建图像。为此,提出了投影驱动的系统模型,并设计了一种将CT迭代图像重建与CS理论相结合的重建算法;为检验重建算法性能,分别对圆周扫描扇束和锥束投影得到的极稀疏投影数据进行了图像重建仿真实验;仿真实验结果表明,在极稀疏投影数据的条件下,算法数值精度高,计算复杂度低,内存开销少,有很强的工程实用性。
1 理论与方法
1.1 基于压缩感知的CT图像重建
CS理论指出,如果信号是稀疏可压缩的,那么就可以使用远低于Nyquist频率的抽样频率对原始信号进行抽样,并且能精确恢复出该信号。基于此,稀疏投影角度下的CT迭代图像重建,可以看成是求解如下不适定线性方程组问题[13]。

式中:Ψf为待重建图像f的稀疏化表示。
1.2 投影驱动的系统模型
在CT迭代图像重建中,为了确定系统矩阵W 元素,必须建立合理的系统模型(即正/反投影运算模型)。系统模型对CT迭代图像重建的数值精度和重建图像质量都有着重要影响。目前,主流的系统模型主要分为3类:像素驱动模型、射线驱动模型和距离驱动模型。像素驱动模型和射线驱动模型分别容易在投影域和图像域引入高频伪影;而距离驱动模型则充分利用存储空间的顺序访问模式,算法复杂度相对较低,能够避免图像域伪影和投影域伪影[14-15]。结合像素驱动和射线驱动模型的优点,并基于距离驱动模型的基本思想,提出了如下投影驱动的系统模型(即投影驱动的正/反投影运算模型)。
1.2.1 投影驱动模型
图1所示的二维扇束投影几何描述了投影驱动的正投影计算过程。在投影角度一定的情况下,将光源分别与某行像素边界的中点与检测器单元的边界相连接,得到它们各自在公共轴(见图1中的X轴)上的交点;然后在X轴上计算像素交点与相邻检测器交点的重叠长度,并用归一化的重叠长度表示像素对检测器正投影的贡献;依次处理每一行像素。投影驱动的反投影计算也是如此。至此,投影驱动的正/反投影计算策略可概括为:一次迭代处理一个投影角度下的所有像素。
图1也详细地展示了检测器边界di、像素边界pi、检测器上投影值dij、像素值pij之间的关系。需要注意,投影驱动的正/反投影中归一化加权系数计算中的分母不同。正投影计算中,为了更精确地模拟线积分,将加权系数除以投影角度β的余弦值,投影驱动的正投影运算表示为

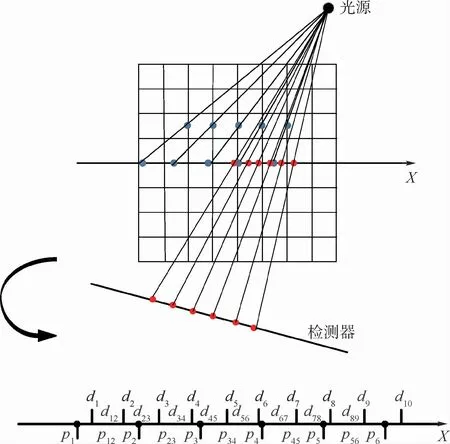
图1 二维扇束投影示意图与细节图Fig.1 Schematic diagram and detailed diagram of two-dimensional fan-beam projection
1.2.2 正/反投影矩阵
在CT迭代图像重建中,正/反投影矩阵将图像域与投影域联系起来。而且,上述正/反投影运算模型(即系统模型)决定了正/反投影矩阵各元素的值。正投影运算g=Wf将图像从图像域映射到投影域,W 为正投影矩阵(即前文所述的系统矩阵);f和g的含义前文已提及,分别为待重建图像和投影数据列矢量。式(5)所示的反投影运算将投影数据从投影域映射到图像域,M 为反投影矩阵。

正/反投影矩阵W 和M 的结构一致,但矩阵元素不同。图2为正/反投影矩阵元素示意图。结合图2,进一步阐述正/反投影矩阵各元素的含义。
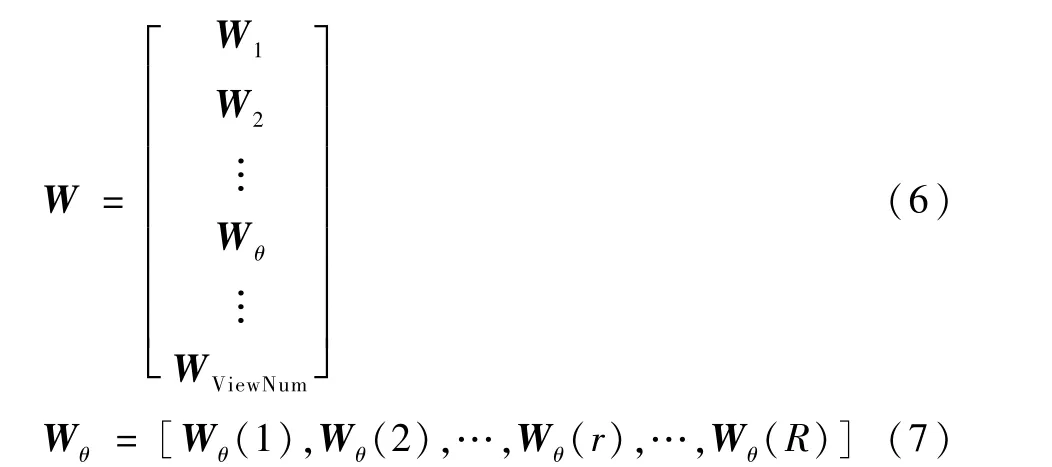
正投影矩阵W 的结构如图2所示。图中:ViewNum为投影角度数;R为像素行数;C为像素列数。Wθ为正投影矩阵W 在第θ个投影角度的子矩阵;Wθ(r)为在第θ个投影角度下第x行像素对所有检测器单元的相对贡献值,矩阵元素为式(3)中的加权系数。式(6)和式(7)清楚地揭示了以上3个矩阵的关系。 式(5)表明反投影矩阵M 的转置MT直接参与反投影运算,矩阵MT的结构如图2所示。与正投影类似,MTθ为矩阵MT在第θ个投影角度的子矩阵,MTθ(r)为在第θ个投影角度下,全部检测器单元对第r行像素的相对贡献值,矩阵元素为式(4)中的加权系数。以上3个矩阵的关系还可以由式(8)和式(9)表示。

1.3 压缩感知的投影驱动CT图像重建
在CS理论框架下,综合传统CT迭代图像重建技术的优势,并利用上述投影驱动系统模型,设计了一种CT迭代图像重建算法,称作CS的投影驱动CT图像重建(Compressed Sensing View Driven CT image reconstruction,CSVD)算法,算法由基于投影驱动模型的粗略图像重建和最优化计算2个环节组成。
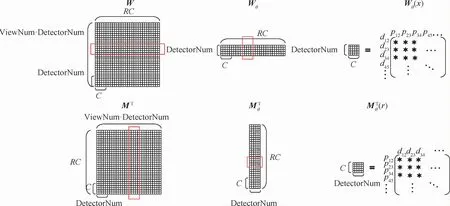
图2 正/反投影矩阵元素示意图Fig.2 Schematic diagram of matrix elements of forward/backward projection

1.3.1 基于投影驱动模型的粗略图像重建
基于投影驱动系统模型,迭代求解不适定的线性方程组g=Wf,以获得众多满足约束项的解。循环2还可以用图3表示,每次循环依次处理每个投影角度下的投影数据;每个角度的投影数据都进行正投影、作差、反投影和校正操作。图中:Wθ和Mθ分别为上文提及的正/反投影矩阵的子矩阵;f(RR)[n,m,θ]为第n次总体迭代的第m次粗略重建子迭代中在第θ个投影角度下的图像向量;Pθ为第θ个投影角度的实际投影数据;φθ为校正因子。
1.3.2 最优化计算


图3 循环2 Fig.3 Loop 2
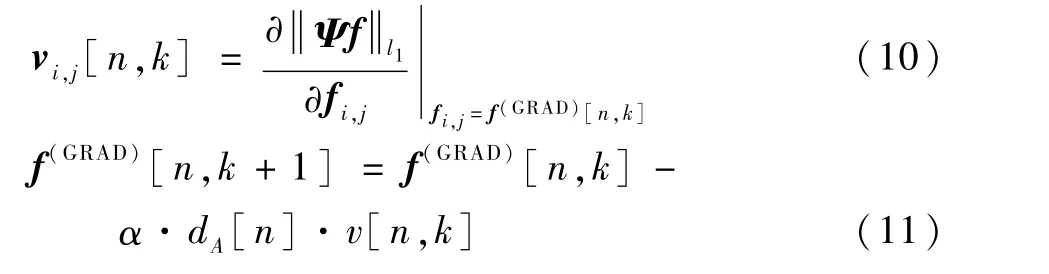
式中:dA[n]为第n次总体迭代中计算得到的平衡因子;第n次总体迭代的第k次最优化子迭代中的图像向量表示为f(GRAD)[n,k];α为步长因子。
2 仿真实验与结果分析
为研究CSVD算法的应用性能,在不同极稀疏投影数据下进行了2组数值仿真实验:圆周扫描扇束投影的二维CT图像重建、圆周扫描锥束投影的三维CT图像重建。上述CT扫描的几何布局如图4所示,另外,综合考虑参数设置对成像质量等多方面的影响,扫描参数的设置以及仿真模型的信息如表1所示。需要注意,圆周轨迹的锥束极稀疏投影扫描方式显然不满足Tuy条件[16],故此算法属于近似的锥束CT图像重建算法。
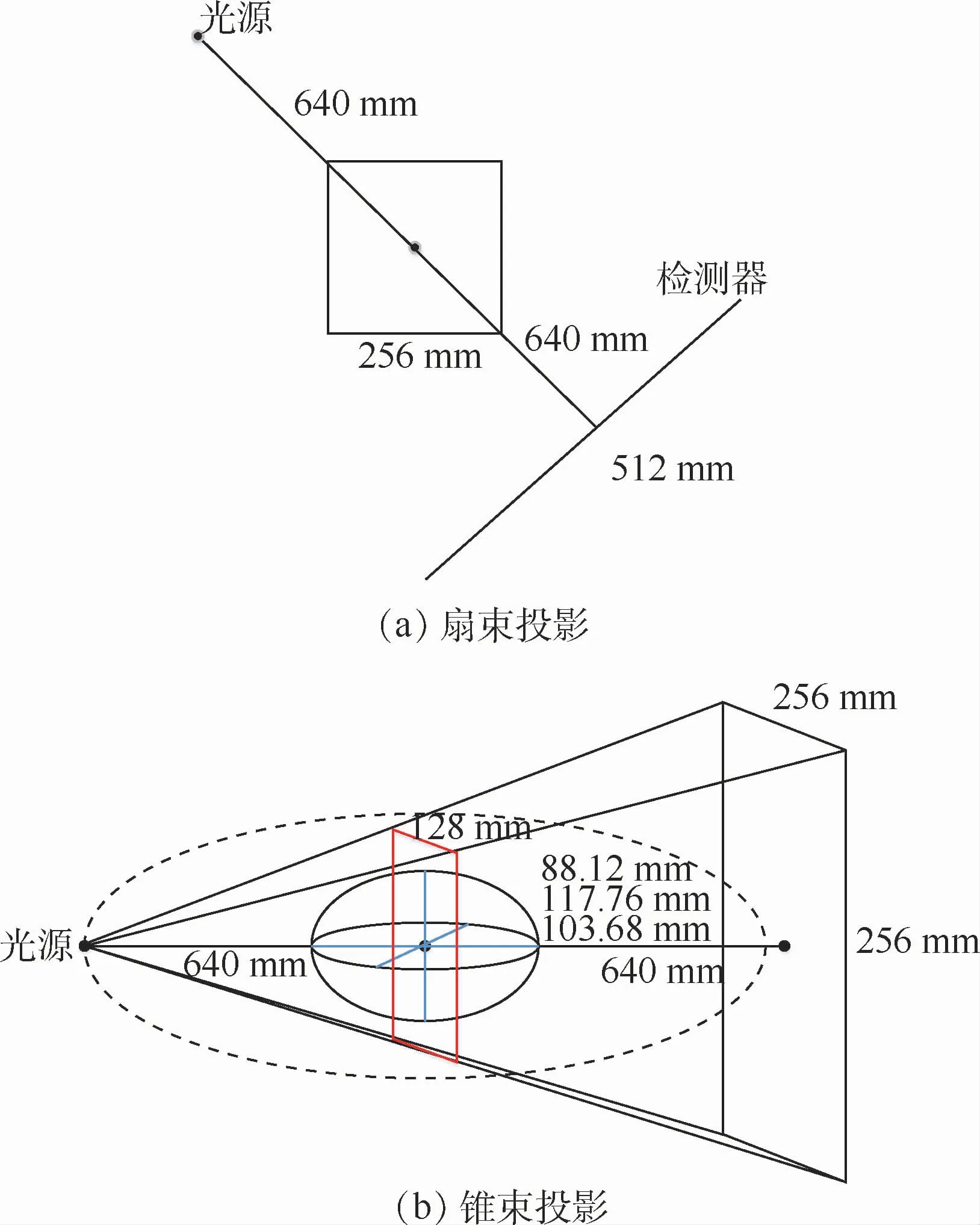
图4 圆周CT扫描系统结构示意图Fig.4 Schematic diagram of circular CT scanning system


表1 CT扫描参数和仿真模型信息Tab1e 1 CT scanning parameters and simu1ation mode1information
2.1 极稀疏投影数据下的二维扇束图像重建
仿真实验先通过对图5(a)所示的Shepp-Logan模型扫描获得投影数据,再使用CSVD算法对该模型在不同投影角度数下进行二维CT图像重建,重建结果如图5(b)所示。为了更精确地比较重建图像与原始图像的像素值,图5(c)给出两者在水平方向上图像的中心像素值分布。重建图像和像素值分布曲线显示,36和20个投影角度下的重建图像与参考图像几乎相同、像素曲线几乎重合;18个投影角度下的重建图像部分边缘模糊且部分区域有块状伪影,但是各个组织结构都能清晰分辨,像素值分布曲线在像素值跳变部位有冲激,其他部分与参考图像曲线几乎重合。
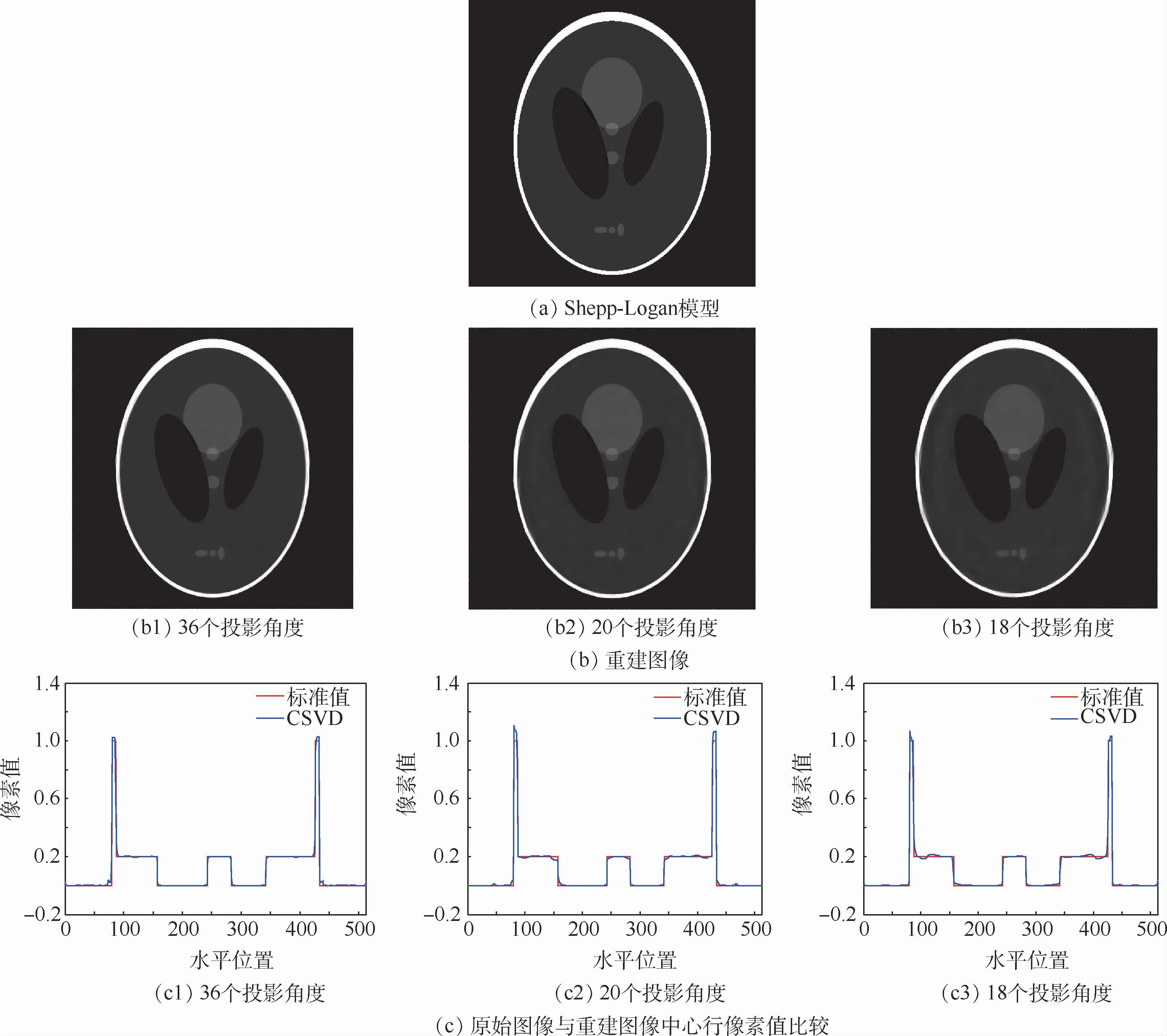
图5 Shepp-Logan模型和重建图像及其中心行像素值比较Fig.5 Shepp-Logan model and reconstructed images,as well as comparison of pixel values of center row between them
为进一步检验CSVD算法在极稀疏投影数据下的重建性能,使用标准均方根误差(Normalized Root Mean Squared Error,NRMSE)、峰值信噪比(Peak Signal to Noise Ratio,PSNR)、全局质量指标(Universal image Quality Index,UQI)[17]3种衡量标准对3种算法(FBP算法、ART-TV 算法和CSVD算法)的重建质量进行客观评价,结果如图6所示。实验结果表明:CSVD算法在各项指标上明显优于其他2种算法,说明CSVD算法在重建图像精确度、噪声抑制和图像恢复程度等方面有着更好的性能。
最后给出以上3种算法在20个投影角度下的3种衡量指标具体数值以及重建时间,如表2所示。与FBP算法相比,CSVD算法耗费了较多的时间,但是CSVD算法在不完全投影数据下的重建性能明显优于FBP算法。与ART-TV算法相比,CSVD算法的重建效率提高了2倍多,同时从以上3种衡量指标可以看出CSVD算法的重建质量有明显提升。
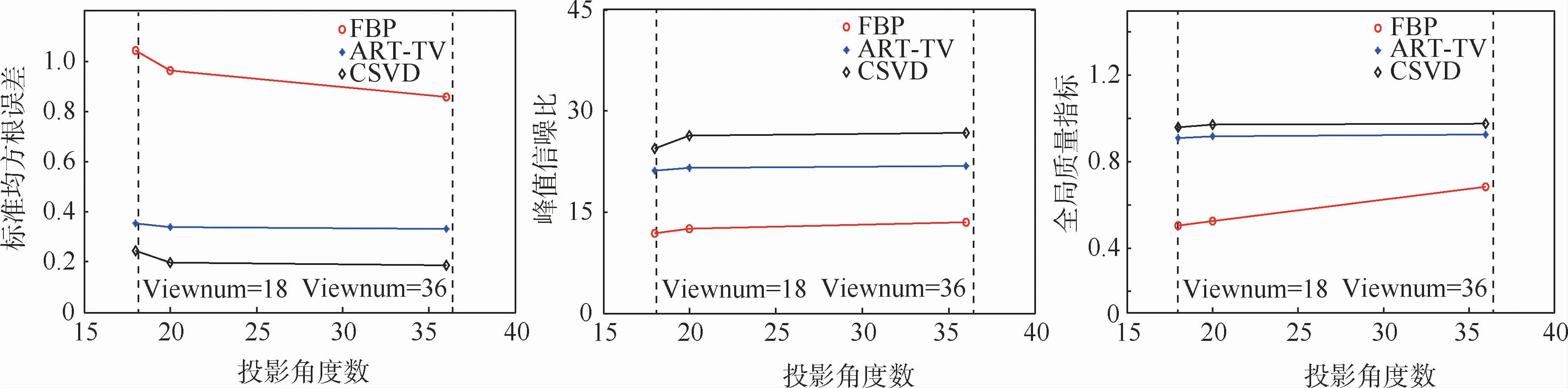
图6 各个投影角度数下不同算法的重建图像质量对比Fig.6 Comparison of reconstructed image quality of different algorithms under various projection angles
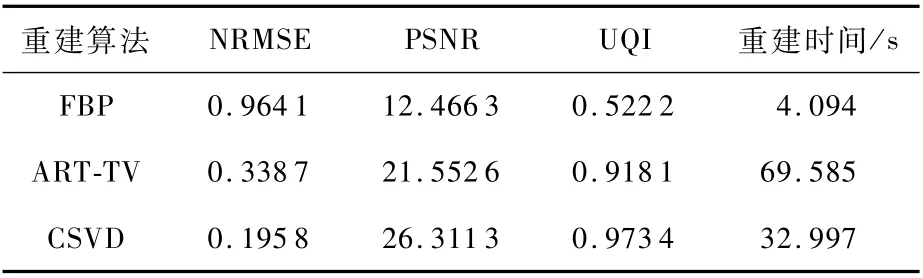
表2 各个投影角度数下不同算法的重建结果Tab1e 2 Reconstruction resu1ts of different a1gorithms under various projection ang1es
2.2 极稀疏投影数据下的三维锥束图像重建
与二维扇束图像重建实验类似,首先对自定义的三维Shepp-Logan模型扫描获得投影数据,该模型透视图如图7(a)所示;其次,使用CSVD算法对该模型分别在20和18个投影角度数下进行三维图像重建,获得中间6层(125层至130层)的横断面切片,选取其中的第125层和128层的重建结果作为展示,如图7所示,其中图7(b)、图7(c)分别为20和18个投影角度下的重建图像,同时还比较了第128层重建图像与参考图像在水平方向上图像中心像素值,得到的像素分布曲线与图5(c)类似,这里不再列出;最后,为了更客观地评价重建图像的质量,使用NRMSE、PSNR、UQI三种衡量标准对第128层重建图像质量进行分析如表3所示。
重建结果表明:在极稀疏投影数据的条件下,CSVD算法表现出良好的重建性能。在仅有18个投影角度的前提下,除重建图像边缘较模糊外,各个组织结构仍能清晰分辨,像素值分布曲线重合度高,且在NRMSE、PSNR、UQI这3项指标上与20个投影角度相当。
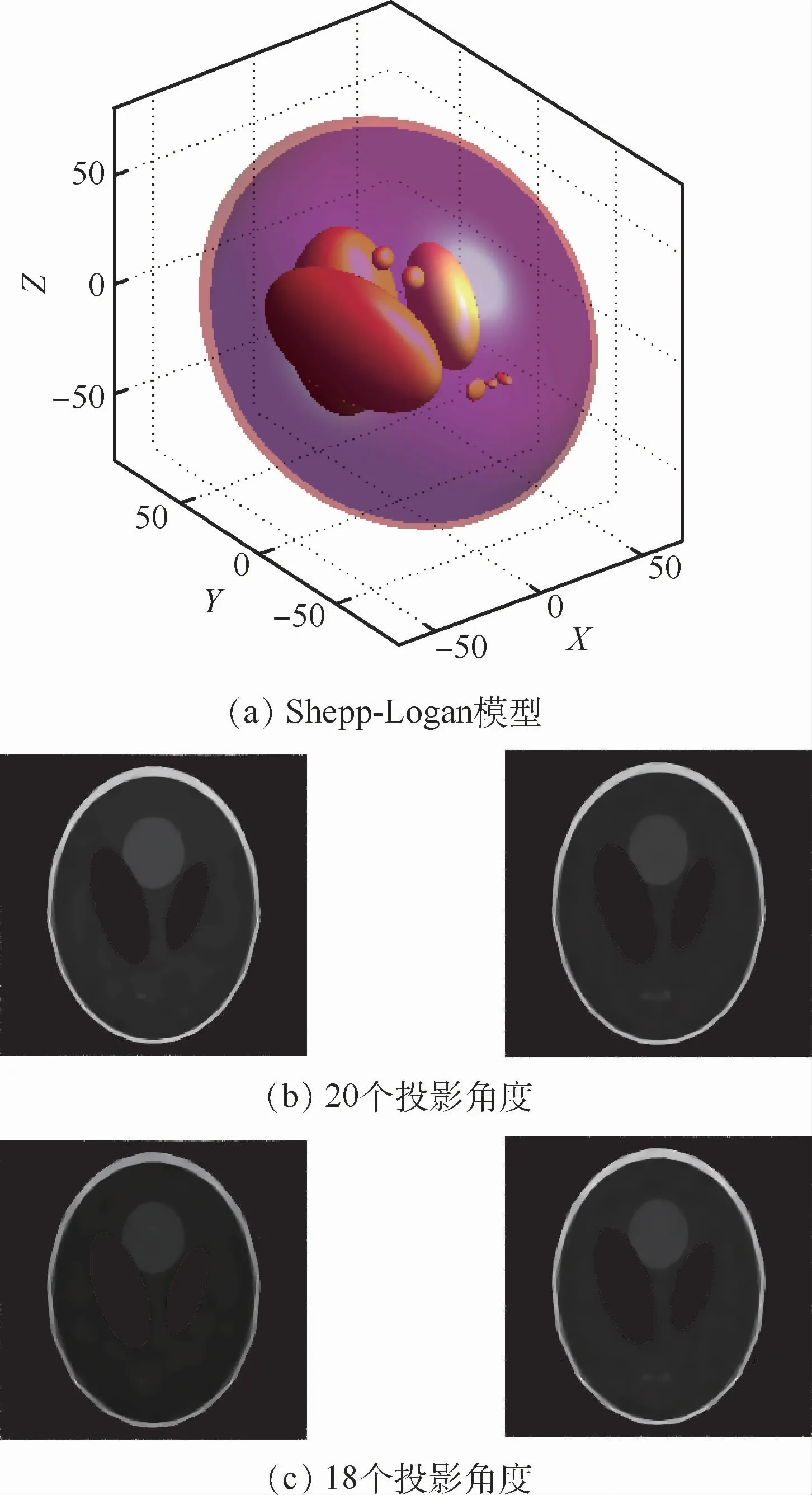
图7 Shepp-Logan模型透视图和重建图像(第125层和128层)Fig.7 Perspective of Shepp-Logan model and reconstructed images(125th and 128th layers)
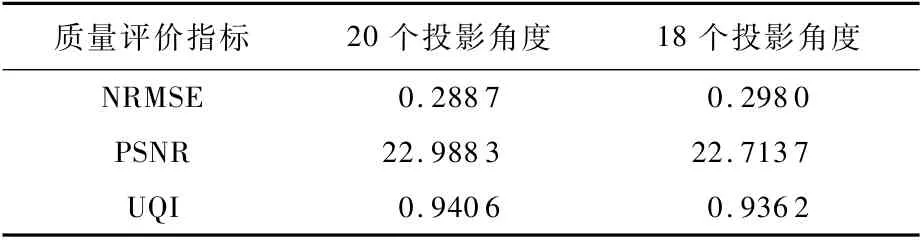
表3 CSVD算法重建图像质量评价Tab1e 3 Qua1itv eva1uation of reconstructed images using CSVD a1gorithm
3 结 论
研究如何在极稀疏投影数据情况下进行CT迭代图像重建具有重要的临床意义。理论分析与仿真实验结果都表明,CSVD算法能够从极稀疏投影数据足够精确地重建断层图像,从而将能够在显著降低CT检查X-射线辐射剂量的前提下,提供充分适宜影像学临床诊断需求的重建图像。CSVD算法良好的图像重建性能主要体现在:
1)数值精度高。仿真实验结果表明:极稀疏投影角度数下的重建图像精确地再现了参考图像的图像结构及像素分布,另外CSVD算法的各项图像质量衡量指标明显优于ART-TV算法和FBP算法。
2)计算复杂度低。由前文的理论分析可知,CSVD算法一次迭代会处理一个投影角度,且在一个投影角度下,只需一次迭代就可以获得一行像素对所有检测器单元的贡献(正投影过程),减少了大量不必要的遍历运算,使得计算复杂度大幅度降低。
3)内存开销少。在医学成像应用中,系统矩阵的规模通常都很大,致使基于其他系统模型的CT迭代图像重建一般都需要存储系统矩阵,而基于投影驱动系统模型的图像重建则不需要对系统矩阵进行存储,大大减小了内存的开销,CSVD算法有着很强的工程实用性。
总之,在极稀疏投影数据的条件下,CSVD算法数值精度高,计算复杂度低,内存开销少,有很强的工程实用性。这给相关领域的科研工作者在极稀疏投影数据情况下进行CT迭代图像重建(从而可以降低CT检查的X-射线辐射剂量)提供了一条切实的技术途径。

