基于Hami1ton体系的Lagrange方程盒式倾转旋翼无人机建模

吴翰，王正平，*，周洲，2，王睿

（1.西北工业大学 航空学院，西安710072； 2.西北工业大学 无人机特种技术重点实验室，西安710065）

随着“V-247”、“鹰眼”等倾转旋翼飞行器的产生，飞行器的发展已由传统的单一模式逐步向变体以及多功能多用途模式发展。倾转旋翼飞行器属于变体类飞行器的一大重要分支，目前国内外众多学者已经对倾转旋翼飞行器的布局、气动［1］及结构［2］进行了深入的研究。针对其动力学模型，国内文献［3-5］和国外文献［6］分别基于牛顿-欧拉方程建立了倾转旋翼飞行器的六自由度模型。由于倾转旋翼飞行器的结构以及动力学特征均较为复杂，因此基于牛顿-欧拉方程的单刚体动力学建模方法在建立倾转旋翼飞行器动力学模型时较为复杂。针对以上情况，本文主要提出以下问题：①对于倾转旋翼飞行器而言，其在倾转过程中飞行器的质心位置和转动惯量均将发生变化，因此如何较为方便地引入动态倾转过程中飞行器质心位置与转动惯量变化对飞行器动力学的影响，值得研究；②对于结构、动力系统较为复杂的飞行器，现有牛顿-欧拉方程基于单刚体思路建立其动力学模型较为复杂，因此能否找寻新的建模方法更为模块化地建立此类飞行器的动力学模型。

为了解决上述问题，本文依照多体动力学［7-8］思路，将算例盒式倾转旋翼无人机划分为由机翼、倾转旋翼、机体、涵道风扇组成的多刚体系统，其中倾转旋翼可绕转动轴发生转动。随后，建立不同刚体部件的力和力矩模型，建立该多刚体系统——盒式倾转旋翼无人机的非保守力和力矩动能模型、势能模型、余虚动模型和逆势能模型；最后采用Hamilton体系下的Lagrange方程［9-10］和第二类Lagrange方程 分别建立该多刚体系统——盒式倾转旋翼无人机的动态倾转过程进行了相应的动力学分析。倾转旋翼无人机动态倾转过程中的质心位置和转动惯量的变化，实质上都是动态倾转过程中倾转旋翼部分的变化所引起的，因此本文将倾转旋翼无人机划分成多刚体系统，通过倾转旋翼刚体部分质心与机体质心之间的位矢变化来引入动态倾转过程中质心位置变化对无人机动力学的影响，通过倾转旋翼刚体部分转动惯量的变化来引入动态倾转过程中转动惯量变化对无人机动力学的影响。本文将无人机拆分成多个刚体进行动力学建模，除了可以更为精确地引入无人机的质心位置和转动惯量变化外，还可以降低无人机建模的复杂度，多个刚体中的每个刚体分别进行建模，再导入Hamilton体系下的Lagrange方程中建立无人机六自由度模型，建模更具有模块化。

1 运动学模型

1.1 参考坐标系建立

本文所选算例为某盒式倾转旋翼无人机，其主要由盒式翼布局、涵道风扇以及倾转旋翼组成。首先基于多体动力学对该盒式倾转旋翼无人机进行相应假设；其次将该盒式倾转旋翼无人机划分为1号机翼、2号机翼、3号机翼、4号机翼、1号涵道风扇、2号涵道风扇、机体、1号倾转旋翼以及2号倾转旋翼共计9个刚体；最后以各刚体的质心为坐标原点建立右手坐标系，选取Fe作为地面参考坐标系，具体如图1所示。需要特别说明的是，本文将左右垂尾与起落架结构共用体和无人机机体共同划分到无人机的机体模块中，关于无人机的航向操纵问题，主要采用1号倾转旋翼、2号倾转旋翼进行差动控制，因此本文的实质仍然是六自由度模型。

所选算例盒式倾转旋翼无人机主要具有垂直起降、动态倾转以及巡航3个运动过程。垂直起降过程由1号涵道风扇、2号涵道风扇、1号倾转旋翼和2号倾转旋翼共同产生向上的拉力；动态倾转过程倾转旋翼部分的倾转轴带动1号倾转旋翼和2号倾转旋翼发生倾转，1号涵道风扇、2号涵道风扇转速逐渐减为零；巡航过程1号涵道风扇和2号涵道风扇不发生转动，仅由1号倾转旋翼和2号倾转旋翼提供向前的拉力。该盒式倾转旋翼无人机的任务剖面如图2所示，其倾转旋翼部分倾转轴与机体内部铰接如图3所示。

所选算例盒式倾转旋翼无人机的具体参数如表1所示。

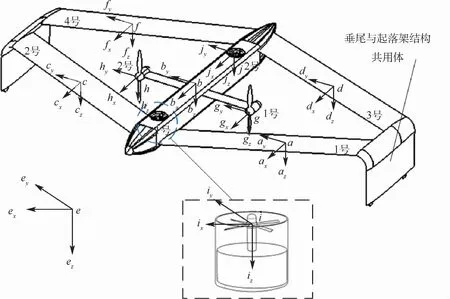
图1 盒式倾转旋翼无人机参考坐标系示意图Fig.1 Schematic diagram of reference coordinate systems for box-wing tilt-rotor UAV

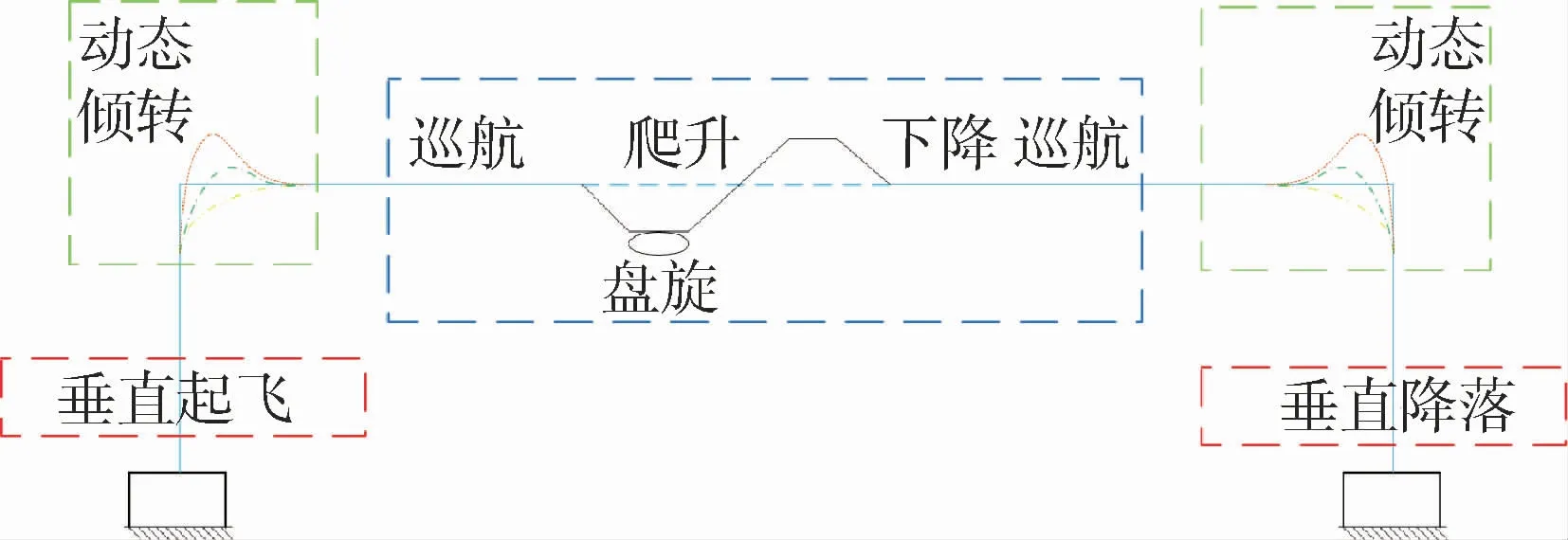
图2 盒式倾转旋翼无人机任务剖面Fig.2 Mission profile of box-wing tilt-rotor UAV

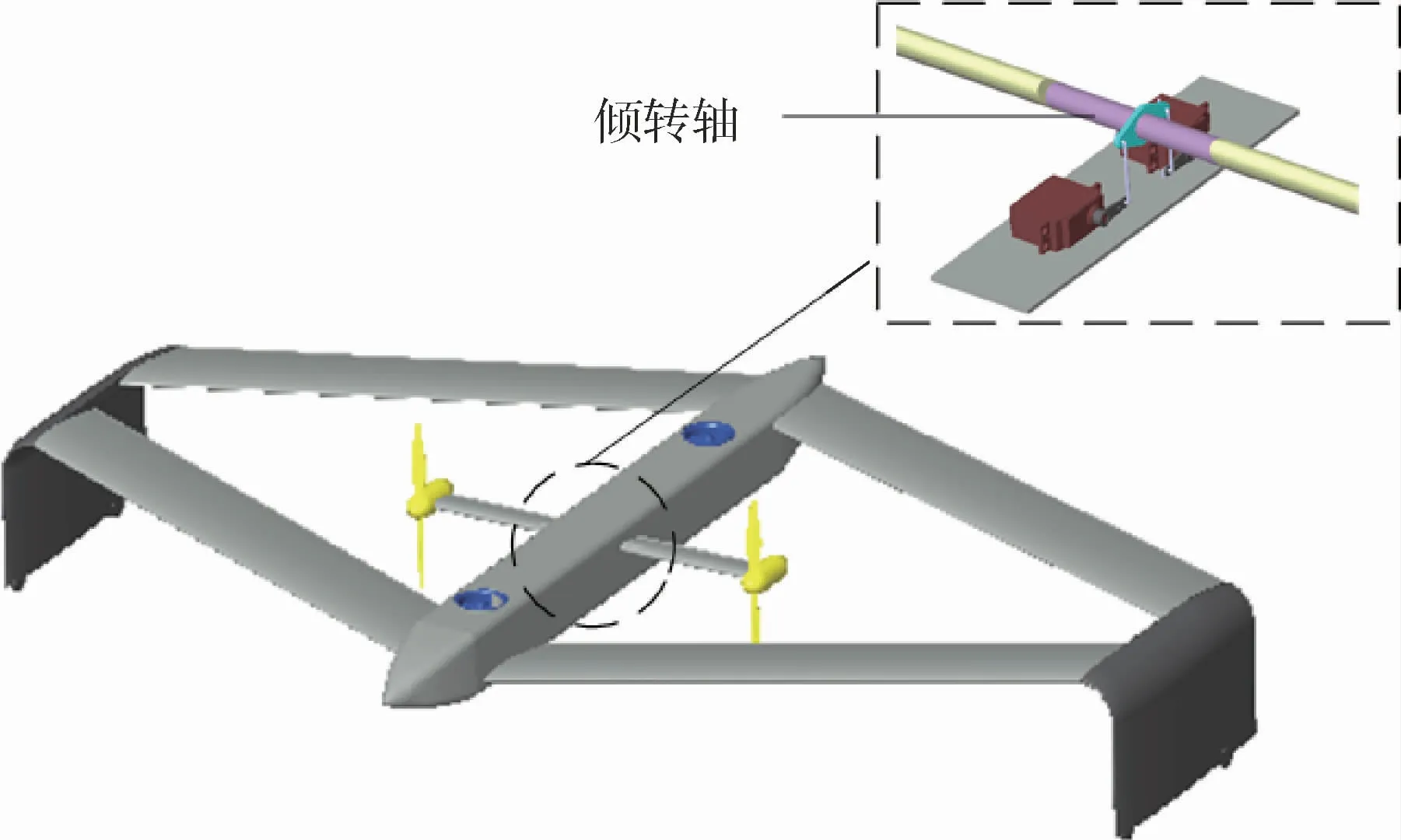
图3 倾转轴与无人机机体内部连接示意图Fig.3 Schematic diagram of internal connection between tilt axis and UAV body

表1 盒式倾转旋翼无人机具体参数Tab1e 1 Specific parameters of box-wing ti1t-rotor UAV

1.2 盒式倾转旋翼无人机广义坐标选取

本文选取用于描述该盒式倾转旋翼无人机动力学特征的广义坐标为

式中：q为盒式倾转旋翼无人机的广义坐标矩阵；reb为盒式倾转旋翼无人机机体质心到参考坐标系原点的位移；qeb为盒式倾转旋翼无人机机体坐标系相对于参考坐标系的姿态，在此选用欧拉角进行姿态参数化。

2 盒式倾转旋翼无人机非保守力和力矩模型建立

2.1 机翼气动力和力矩模型

由于无人机的旋翼一般较小，因此在建立该盒式倾转旋翼无人机机翼的气动力和力矩模型时忽略倾转旋翼尾流对于机翼的影响。由于本文无人机较小，因此在进行机翼的气动力和力矩建模中，未考虑前后机翼之间的相互气流干扰影响。以盒式倾转旋翼无人机的1号机翼为例，由于盒式倾转旋翼无人机的任务剖面中存在垂直起降、动态倾转和前飞巡航3个运动过程，因此其机翼将从90°的大迎角逐步过渡为小迎角，为了建立其动力学模型，可参考文献［12］选取机翼失速迎角作为分界线，将其动力学模型划分为大迎角和小迎角两部分，小迎角部分与正常飞行时一样，在此不再给出，大迎角部分通过平板扰流系数 进行建立，具体形式为［14］

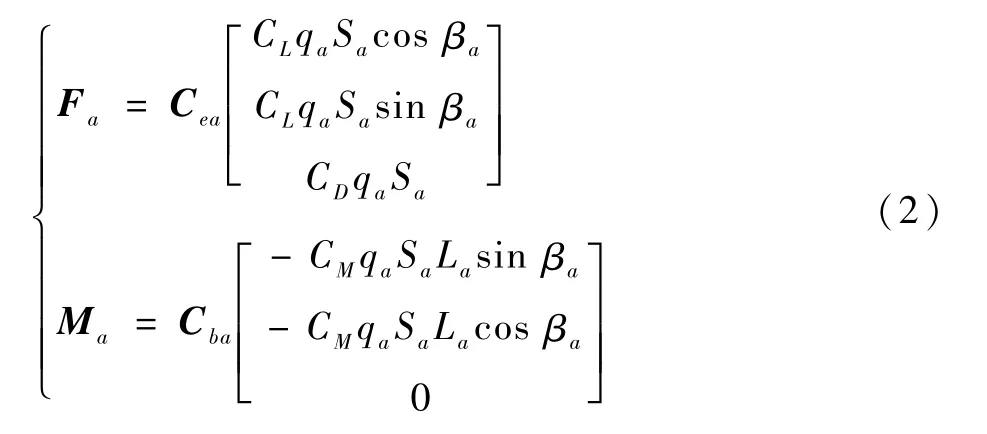
式中：Cea为1号机翼坐标系向参考坐标系的转换矩阵；Cba为1号机翼坐标系向机体坐标系的转换矩阵；qa为1号机翼动压；βa为1号机翼侧滑角；La为1号机翼参考长度；Sa为1号机翼参考面积；CL为平板扰流升力系数；CD为平板扰流阻力系数；CM为平板扰流力矩系数。同理可得无人机2号机翼、3号机翼、4号机翼和无人机机体的气动力和力矩模型为：Fc，Fd，Ff，Fb；Mc，Md，Mf，Mb。需要注意的是，无人机机体的气动力和力矩模型包含左右垂尾与起落架结构共用体的气动力和力矩模型。可以通过无人机机体质心与左右垂尾与起落架结构共用体质心之间的位矢，将左右垂尾与起落架结构共用体的气动力和力矩模型转换至无人机的机体质心处。

2.2 倾转旋翼气动力和力矩模型

倾转旋翼部分可通过旋翼倾转轴绕无人机机体坐标系的Y轴发生偏转，假设偏转角为θ，则倾转旋翼坐标系向无人机机体坐标系的转换矩阵为

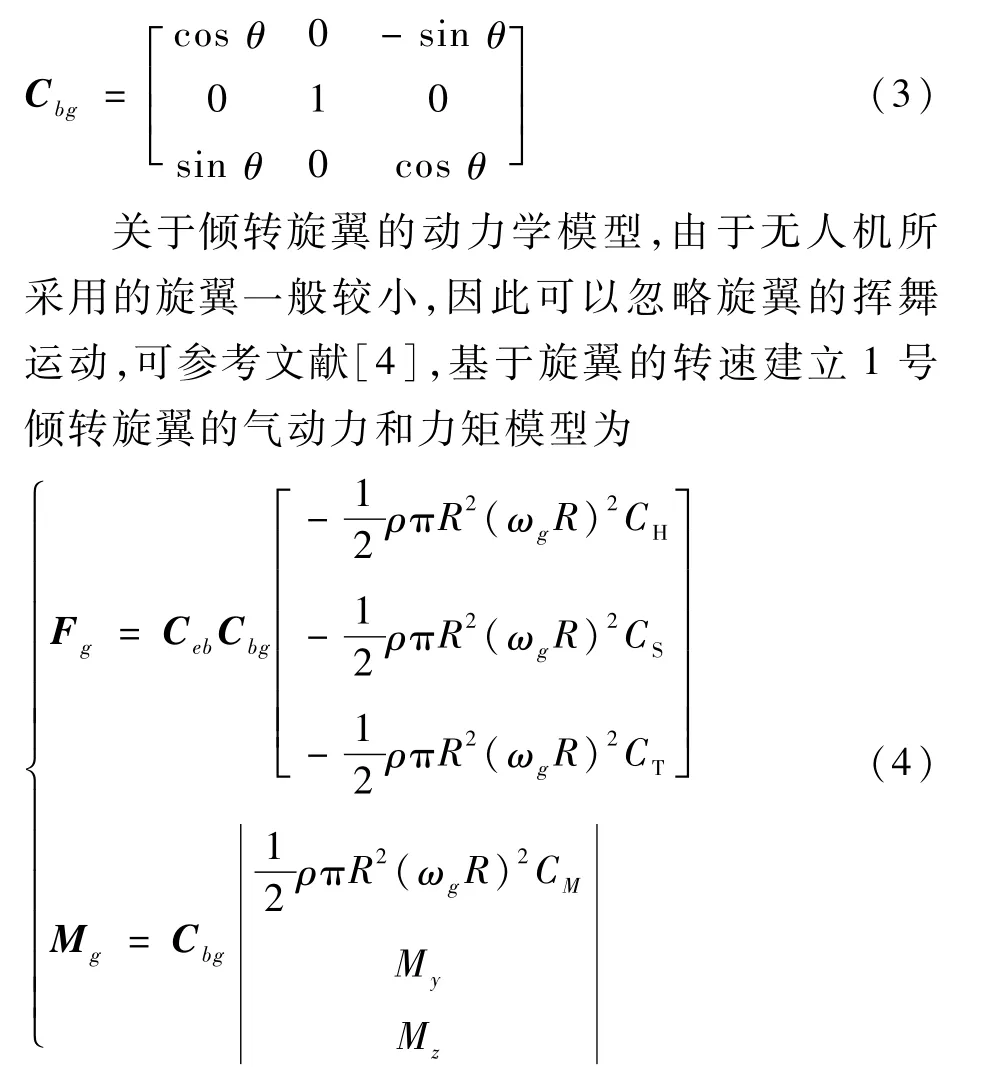
式中：Cbg为1号旋翼坐标系向无人机机体坐标系的转换矩阵；Ceb为机体全标系向地面坐标系的转换矩阵；R为1号旋翼的桨叶半径；ωg为1号旋翼的转速；CM为1号旋翼的力矩系数；My、Mz为1号旋翼的力矩分量；CH、CS、CT为1号旋翼的力系数；ρ为大气密度。同理可得2号倾转旋翼的气动力和力矩模型为：Fh，Mh。

2.3 涵道风扇气动力和力矩模型

涵道风扇模型与旋翼模型较为相似，可参考文献［15］，通过增加修正系数的方式基于旋翼动力学模型，来建立1号涵道风扇的气动力和力矩模型，其具体结果为

式中：Cbi为1号旋翼坐标系向无人机机体坐标系的转换矩阵；K为系数，其与涵道风扇的涵道唇口面积和形状有关；ωi为1号涵道风扇旋转角速度；Ri为1号涵道风扇的桨叶长度；A为1号涵道风扇的投影面积；Cd、CY、CT为涵道风扇力系数；CM为1号涵道风扇的力矩系数；Mx、My为1号涵道风扇力矩分量。同理可得2号涵道风扇的气动力和力矩模型为：Fj，Mj。

2.4 盒式倾转旋翼无人机非保守力和力矩模型

3 Hami1ton体系下Lagrange方程的应用

式中：m为非保守刚体系统的质量；T为刚体系统的动能；J为非保守刚体系统的转动惯量；U为刚体系统的势能；Uq为刚体系统的拟势能；δQH为刚体系统的余虚功；X为刚体系统的质心位移矢量；θ为刚体系统的姿态。

式中：msum为盒式倾转旋翼无人机的总质量；Jsum为盒式倾转旋翼无人机的总转动惯量矩阵；Jg、Jh、Ji、Jj分别为1号倾转旋翼、2号倾转旋翼、1号涵道风扇、2号涵道风扇的惯性矩；Jg、Jh、Ji、Jj分别为1号倾转旋翼、2号倾转旋翼、1号涵道风扇、2号涵道风扇的转动惯量；ωg、ωh、ωi、ωj分别为1号倾转旋翼、2号倾转旋翼、1号涵道风扇、2号涵道风扇的转速。由于动态倾转过程中倾转旋翼部分的转动惯量矩阵将发生变化，因此本文通过Jg和Jh在无人机的动态倾转过程中随时间发生变化，而引入动态倾转过程转动惯量变化对于无人机动力学的影响。

该盒式倾转旋翼无人机的势能［18］为

式中：veb为盒式倾转旋翼无人机机体质心到参考坐标系原点的线速度矩阵；ωeb为盒式倾转旋翼无人机机体坐标系相对于参考坐标系的角速度矩阵。

再对式（17）运用Green定理可得

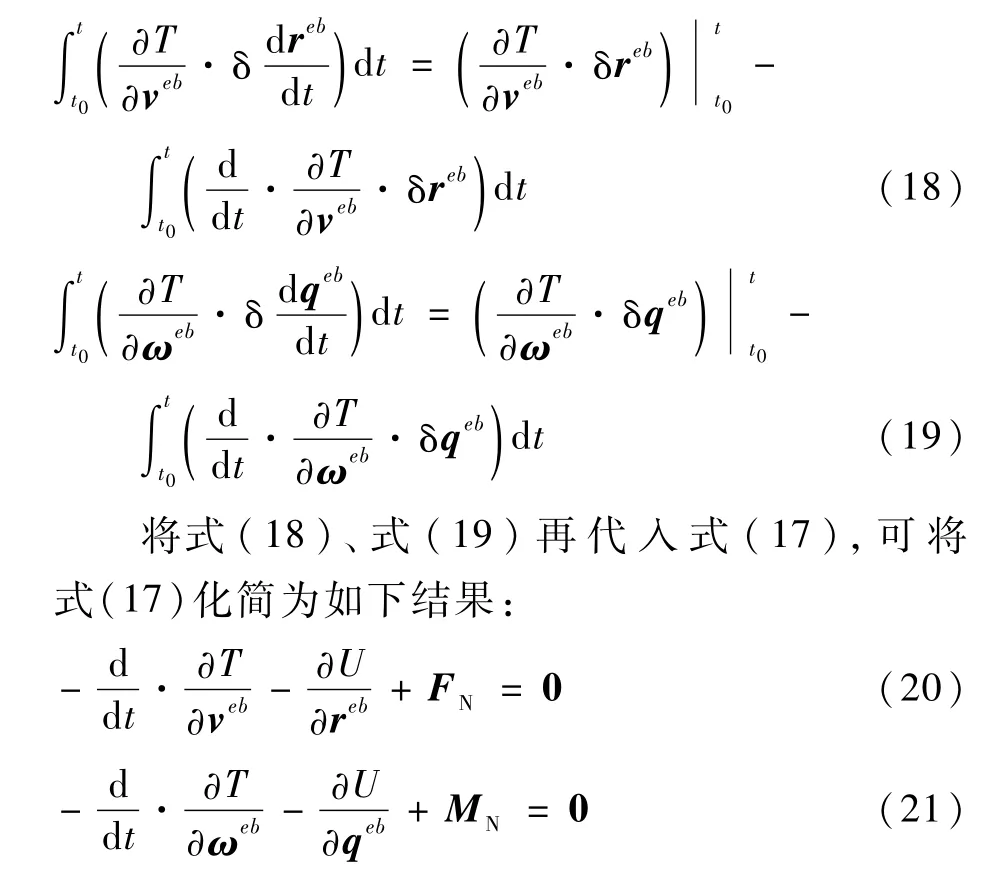
式（20）和式（21）即为盒式倾转旋翼无人机的动力学模型。其中，式（20）主要描述的是该无人机的质心线加速度与无人机非保守力、保守力之间的关系；式（21）主要描述的是该无人机的角加速度与无人机非保守力矩、保守力矩之间的关系。

4 第二类Lagrange方程的应用

为了与Hamilton体系下的Lagrange方程建模结果进行对比，本文同样采用第二类Lagrange方程进行该盒式倾转旋翼无人机的动力学建模，第二类Lagrange方程的具体形式［20］为

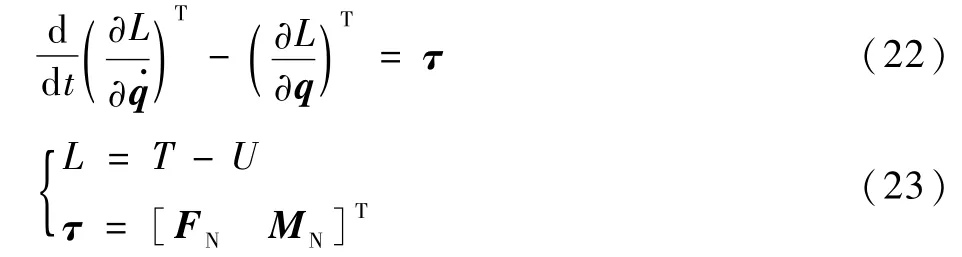
式中：L为拉格朗日函数；T为无人机动能模型；U为无人机势能模型。第二类Lagrange方程中字母的含义与上文一致，将式（6）、式（10）、式（13）代入式（22）即可得到基于第二类Lagrange方程所建立的盒式倾转旋翼无人机的动力学模型。

5 数值仿真

5.1 实验验证

首先为了验证本文建模方法的合理性，采用Hamilton体系下Lagrange方程建模方法、第二类Lagrange方程建模方法和传统牛顿-欧拉方程单刚体方法对盒式倾转旋翼无人机进行动力学建模，并与该盒式倾转旋翼无人机的飞行实验数据进行对比，实验无人机的构型具体如图4所示。

图4 实验盒式倾转旋翼无人机示意图Fig.4 Schematic diagram of experimental box-wing tilt-rotor UAV

该盒式倾转旋翼无人机主要进行了滑跑起飞、巡航飞行以及滑跑着陆的实验过程，本文选取无人机爬升到巡航阶段的实验数据与数值仿真结果进行对比，其中所选取对比的无人机初始时刻实验数据为：无人机初始高度1 m，前飞速度10 m／s，上升速度0.3 m／s，俯仰角5°，其余参数均为零。在实验过程中，无人机左右螺旋桨转速位于2000～2500 r／min之间。基于Hamilton体系下Lagrange方程、第二类Lagrange方程以及牛顿-欧拉单刚体方法所建动力学模型的数值仿真初始条件均为：reb＝［0 0－1］Tm，qeb＝［0 5 0］T（°），veb＝［10 0－0.3］Tm／s，ωeb＝［0 0 0］Trad／s。具体对比结果如图5～图7所示。需要特别说明的是，3次仿真实验和实物实验采用的均为PID控制方法进行控制，其目标轨迹为飞行高度60 m，前飞速度20 m／s，俯仰角不进行控制。

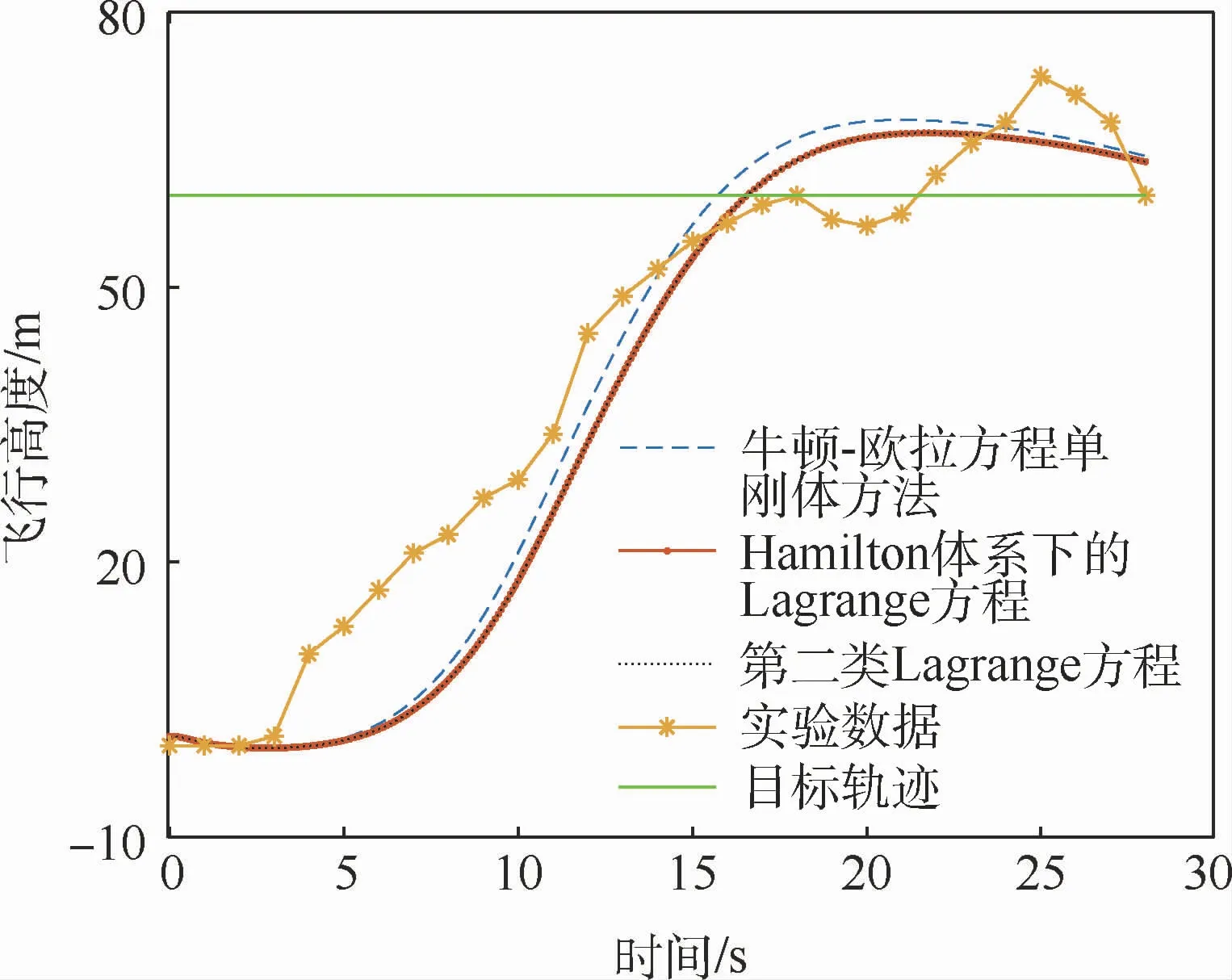
图5 无人机飞行高度仿真与实验结果对比Fig.5 Comparison of UAV flight height between simulation and experimental results

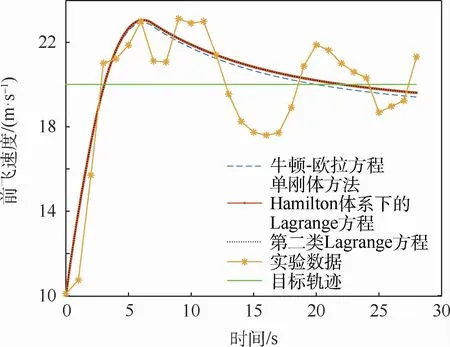
图6 无人机前飞速度仿真与实验结果对比Fig.6 Comparison of UAV forward velocity between simulation and experimental results

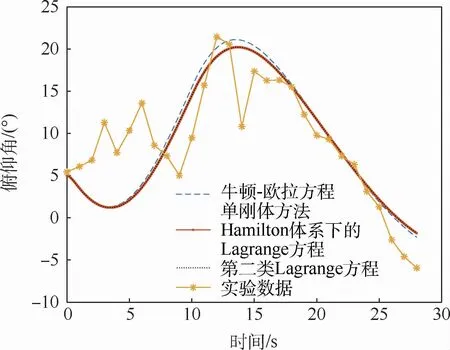
图7 无人机俯仰角仿真与实验结果对比Fig.7 Comparison of UAV pitch angle between simulation and experimental results

通过图5～图7数值仿真结果与飞行实验数据的对比可以得出以下结论：首先，图5～图7中Hamilton体系下Lagrange方程、第二类Lagrange方程、牛顿-欧拉方程以及实验数据的趋势基本一致，这些均验证了本文动力学建模方法可适用于该无人机的动力学建模，且所建模型是合理的。其次，通过图5～图7中Hamilton体系下Lagrange方程和第二类Lagrange方程仿真结果的一致性，可以验证在相同的非保守力和力矩模型下，这2类建模方程的结果是一样的，但是牛顿-欧拉方程单刚体仿真结果与Hamilton体系下Lagrange方程和第二类Lagrange方程仿真结果存在差异，其主要原因为：单刚体和多刚体建模方法无人机的转动惯量和质心位置存在不同。除此之外，图6中实验数据与仿真结果略有差异，其主要原因在于：在飞行实验过程中，盒式倾转旋翼无人机左右螺旋桨的转速保持在2 000 r／min～2 500 r／min之间，而不是完全固定在某一数值，因此其会导致盒式倾转旋翼无人机前飞速度实验数据与仿真结果的差异。

5.2 动态倾转阶段数值仿真

5.1节已验证本文模型的合理性，本节将本文所建模型应用于盒式倾转旋翼无人机，对其最为关注的动态倾转阶段进行动力学仿真研究。由于5.1节已验证Hamilton体系下Lagrange方程和第二类Lagrange方程在非保守力和力矩模型相同的情况下，建模结果一致，因此在本节仿真曲线中将不再引入第二类Lagrange方程的仿真结果。需要说明的是，本文所选样机目前仅进行了滑跑起飞以及巡航试验，还未实现垂直起飞及倾转过渡功能。因此，在本节动态倾转过程研究中，并未进行试验数据与仿真数据的对比。

倾转旋翼无人机动态倾转过程时间的长短会影响其动态倾转阶段的动力学特征，为了进行对比找寻最为合适的动态倾转方式，分别选取倾转过程总时间为5 s、10 s、15 s进行对比，整个仿真过程1 号倾转旋翼、2 号倾转旋翼转速保持2 000 r／min不变，初始时刻其余状态量均为零。整体仿真过程为盒式倾转旋翼无人机由静止开始垂直上升到动态倾转再到巡航，盒式倾转旋翼无人机垂起过程为0～15 s，期间旋翼倾转轴与无人机机体的夹角为0°；动态倾转阶段从15 s开始，期间旋翼倾转轴与无人机机体的夹角由0°线性变为－90°，1号涵道风扇、2号涵道风扇的转速线性减少至零；前飞巡航阶段旋翼倾转轴与无人机机体的夹角为－90°，1号涵道风扇、2号涵道风扇无转速。具体仿真结果如图8～图12所示。

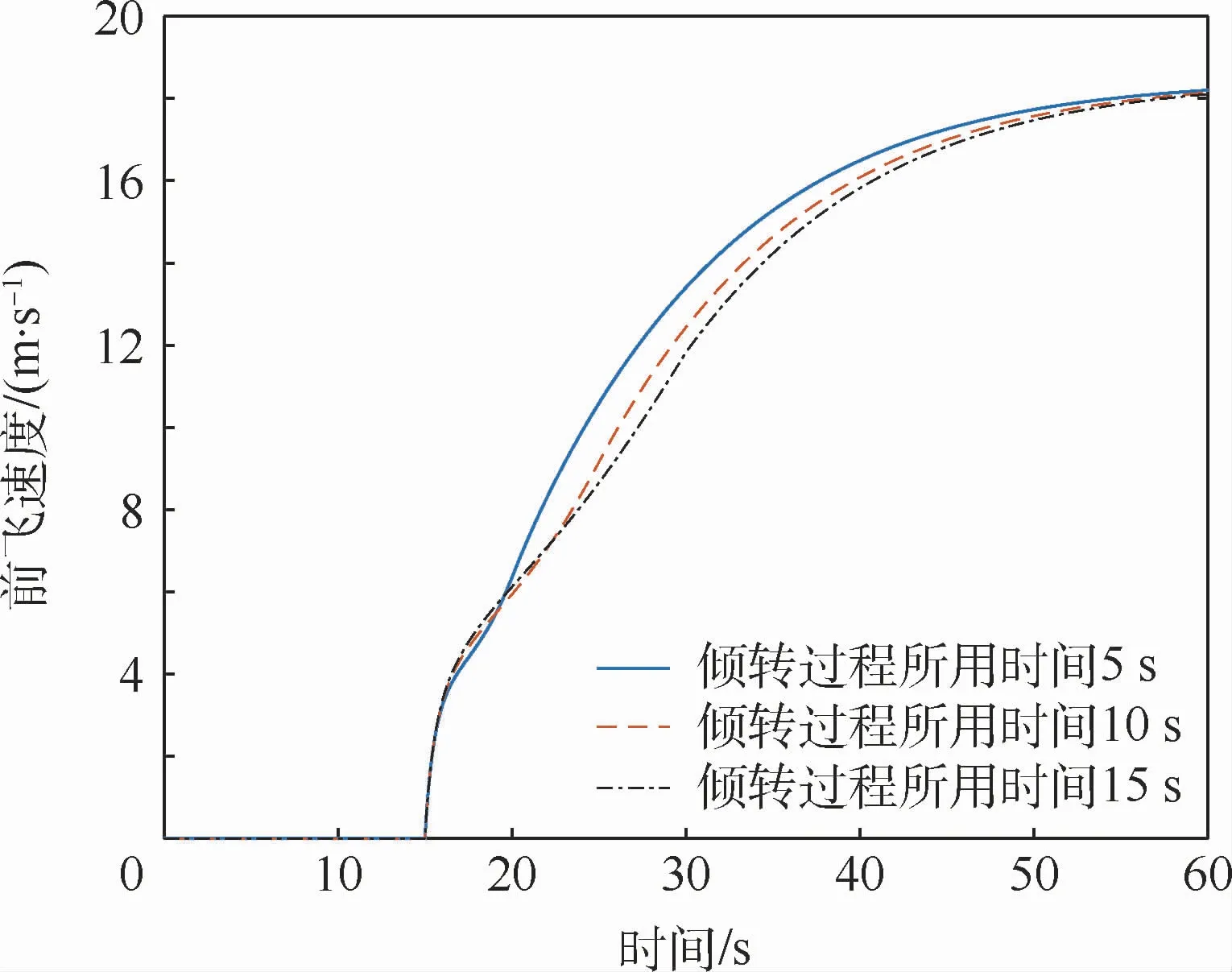
图8 盒式倾转旋翼无人机前飞速度Fig.8 Forward velocity of box-wing tilt-rotor UAV

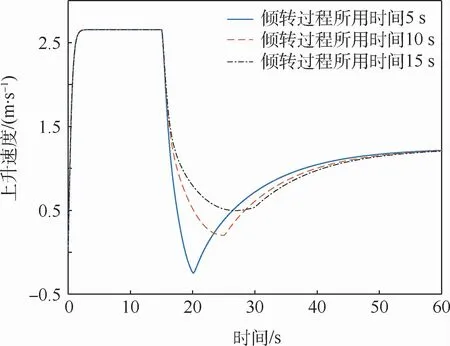
图9 盒式倾转旋翼无人机上升速度Fig.9 Rising velocity of box-wing tilt-rotor UAV

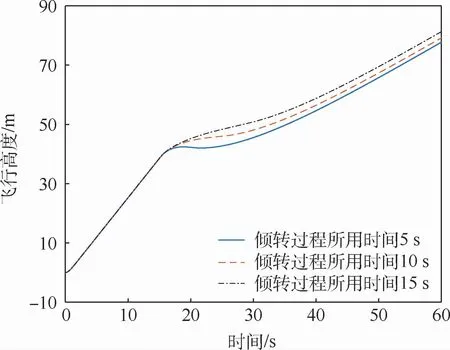
图10 盒式倾转旋翼无人机飞行高度Fig.10 Flight height of box-wing tilt-rotor UAV

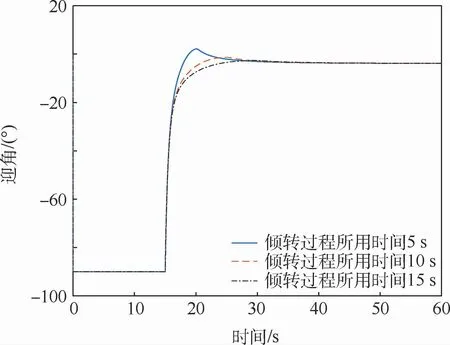
图11 盒式倾转旋翼无人机迎角Fig.11 Angle of attack of box-wing tilt-rotor UAV

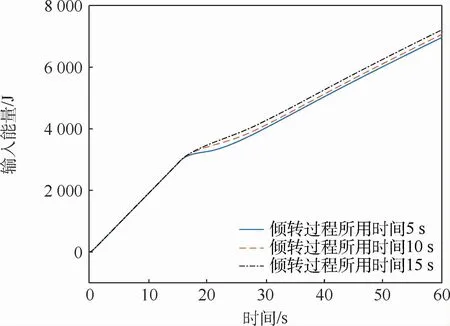
图12 盒式倾转旋翼无人机输入能量Fig.12 Input energy of box-wing tilt-rotor UAV

通过图8～图12仿真结果的对比可以得到，倾转过程所用时间越短，无人机上升速度在动态倾转过程中的突变越大，无人机动态倾转轨迹越不光滑，无人机倾转过程中的掉高越明显，但无人机所需要的输入能量较少；无人机的倾转时间越长，无人机上升速度在动态倾转过程中的突变越小，无人机动态倾转轨迹越光滑，无人机倾转过程中的掉高越少，但无人机所需要的输入能量越多。因此，具体采用何种动态倾转方式，还需要基于本模型的仿真结果，根据无人机的实际应用情况来进行确定。接下来对仿真曲线图8、图11和图12进行解释。由于1号涵道风扇、2号涵道风扇转速减为零这个过程所用时间是和动态倾转过程所用时间一致的，因此倾转时间越长，1号涵道风扇、2号涵道风扇对无人机所做功越多，该盒式倾转旋翼无人机的输入能量越多，这与仿真结果完全一致；由于本文选取无人机的迎角作为参考迎角，因此对于无人机垂起过程而言无人机的迎角为－90°，随后进行动态倾转，最后回归到正常巡航迎角，整体与无人机迎角仿真曲线一致；对于前飞速度而言，无人机在倾转过后前飞速度最终趋于一致，这是由于巡航时仅由倾转旋翼提供拉力，而旋翼转速一致，因此巡航时拉力一致，无人机前飞速度最终结果一致。

6 结 论

通过某盒式倾转旋翼无人机的建模与仿真，可以得到如下结论：

1）本文基于Hamilton体系下的Lagrange方程和第二类Lagrange方程推导并建立了盒式倾转旋翼无人机的动力学模型，并通过与实验结果的对比验证了建模方法的合理性，通过仿真结果可以看出，在相同非保守力和力矩模型的情况下，基于Hamilton体系下的Lagrange方程和第二类Lagrange方程建立的动力学模型的实质是一致的，Hamilton体系下的Lagrange方程能够适用于倾转旋翼飞行器的动力学建模。本文建模的缺点在于：未引入无人机前后机翼之间的干扰和倾转旋翼尾流对无人机后机翼的影响，后续可从这两方面进行改进。

2）Hamilton体系下的Lagrange方程主要是将建模系统离散成多体系统，再分别考虑每个系统的质心位置以及转动惯量变化，最终通过不同刚体间的位移约束引入不同系统质心位置的变化，通过叠加的方式引入不同系统转动惯量的变化，这也是该方法在建立变体类飞行器动力学模型时的优点。除此之外，该方法将无人机划分成多刚体系统，分别建立每个刚体的模型，再导入Hamilton体系下的Lagrange方程建立无人机六自由度模型，其更具模块化，可降低建模的复杂度。

本文研究了倾转过程时间长短对于倾转旋翼无人机动力学的影响，除此之外动态倾转过程中倾转旋翼转速变化、涵道风扇转速变化等均将对倾转无人机的动力学产生影响，因此应当综合考虑这些因素进而制定最为合适和安全的动态倾转过渡方式。