层间间距对平纹双层结构靶体抗侵彻性能的影响
周 熠, 李 杭, 严祥邦, 梁耀庭, 张中威
(1. 武汉纺织大学 纺织纤维及制品教育部重点实验室, 湖北 武汉 430200;2. 陆军工程大学 爆炸冲击防灾减灾国家重点实验室, 江苏 南京 210007)
在弹丸侵彻过程中,柔性防弹服的防弹层通过纤维形变、断裂以及纤维之间的摩擦作用来吸收和转化弹丸动能,从而达到弹道防护的目的。防弹层一般由多层平纹或者无纬布材料相互叠加而成[1-2]。有学者发现,防弹材料层与层之间形变的的相互干扰是决定其抗侵彻性能好坏的重要因素之一[3],同时高性能纤维的损毁呈现出多种形态[4]。在叠层结构中,弹丸容易对迎弹面造成剪切破坏,对背弹面造成拉伸破坏[5-7]。将抗剪切破坏的材料放置在迎弹面,抗拉伸破坏的材料放置在背弹面,可以在一定程度上提升叠层整体的能量吸收,增强其抗侵彻性能[8-9]。这一理论被进一步拓展为背弹面和迎弹面的弹性响应和非弹性响应,并且推导出多层结构中呈现弹性响应和非弹性响应的材料所占的质量比[10]。除此以外,材料的能量吸收效率会随着叠层层数的增加而降低[11]。这是因为迎弹面的横向形变会受到背弹面的影响,导致弹丸在弹着点周围造成应力集中,限制应力在迎弹面上的传递。为了避免迎弹面与背弹面发生相互干扰,提出了2种解决方法:在迎弹面和背弹面的位置使用模量不同的材料;使层与层之间保持一定的间距。
第1种方法的可行性通过力学分析模型在理论上得到了验证[12]。有学者假想出一种双层结构,将模量不同的材料放置在迎弹面与背弹面位置,利用分析模型预测叠层结构的V50(弹丸对靶体击穿概率为50%时的弹道速度)。结果表明,将模量较高的材料放置在背弹面比将其放置在迎弹面更有利于提升双层结构的V50。 通过有限元建模发现,如果将模量较高的材料放置在背弹面,迎弹面与背弹面上的横向形变就不会发生相互干扰,因此高模量的材料就能吸收更多的应变能和动能[13]。针对横向波相互干扰这一现象,有些学者提出了不同的看法。同样是利用有限元软件ABAQUS,Wang等[14-15]建立了层间取向不同的叠层机织物模型。认为改变层与层之间的取向性即排列角度,可以使迎弹面织物与背弹面织物之间的相互干扰变得更加剧烈,有利于结构吸能效果的提升。虽然这一假设同时得到了有限元模型和弹道实验的论证,但是由于报道中的数据可重复性较低,所以这种设计方法的可行性仍然存疑。
第2种方法的设计思路基于如下假设:如果层与层之间的间距大到能够保证前一层材料在完全损毁之前弹丸不与后一层材料接触,那么叠层结构吸收的弹丸动能总量应该等于单层结构所吸收的能量乘以层数[11]。虽然这种设计思路的可行性已被力学分析模型[16]和有限元模型所验证[17],但无论是哪种模型都缺乏实验数据的支持。除了上述工作以外,相关研究在公开的文献中比较缺乏。本文通过弹丸侵彻实验和有限元建模,深入研究层间间距对芳纶平纹双层结构抗侵彻性能的影响,以揭示迎弹面和背弹面材料在不同间距下的动态响应过程和吸能机制。
1 实验材料
本研究使用的芳纶平纹机织物由Kevlar®29(美国杜邦公司)制备而成。芳纶长丝束的线密度为1 580 dtex,平纹机织物经纬密均为70根/(10 cm),面密度为240 g/m2。使用乙烯-醋酸乙烯共聚物(EVA)高弹泡棉作为间隔材料(佛山市益程包装材料有限公司),其密度为18 kg/m3,拉伸模量为0.213 MPa,断裂伸长率为57.88%,断裂强度为0.123 MPa。
2 弹丸侵彻实验
利用贯穿性弹丸侵彻实验对靶体的防弹性能进行表征,实验设备如图1所示。使用直径为8 mm, 质量为2 g的球形弹丸(见图2(a))。弹丸的入射速度在0 ~180 m/s之间。使用红外测速装置捕捉弹丸运行的轨迹,计算出弹丸接触靶体前的入射速度和贯穿靶体后的出射速度。如果忽略空气阻力对弹丸的影响,靶体的抗侵彻性能为
式中:ΔE为弹丸动能损失, J;m为弹丸质量, g;v1和v2分别为弹丸入射速度和出射速度,m/s。

图1 弹丸冲击实验设备示意图Fig.1 Ballistic apparatus
将芳纶织物和EVA高弹泡棉材料裁减成25 cm×25 cm大小,夹持在夹具中。夹具四边铣有沟槽,固定试样四边以避免长丝束发生滑移(见图2(b))。由于夹具沟槽之间的间距为15 cm,所以在弹丸侵彻过程中,平纹织物受到冲击作用的实际面积为15 cm×15 cm。对EVA高弹泡棉材料进行弹道测试发现,泡沫材料不具备抗侵彻性能,因此,使用EVA作为间距材料,不会影响靶体的能量吸收效果。

图2 弹丸与夹具示意图Fig.2 Projectile (a) and clamp (b)
3 有限元模型
使用商业软件ABAQUS对平纹织物的抗侵彻过程进行有限元建模分析,研究织物在弹丸贯穿过程中的横向形变、应力分布和能量吸收的变化规律。模型中弹丸直径与质量分别设定为8 mm和2 g,与实物一致。织物由经纱与纬纱相互交织而成,长丝束由C3D8R六面体实体单元构成。由于模型在X轴与Z轴方向上对称,故只需要将实物图的四分之一建模即可,即织物模型的实际大小为7.5 cm×7.5 cm。长丝束与织物的几何模型如图3所示。将长丝束模型的材料属性设定为各向同性,将弹丸设定为刚体,在与织物的接触过程中不会发生变形。材料的相关参数为:长丝束的屈服应力为2.92 GPa,断裂伸长率为3.6%,弹性模量为70.5 GPa,泊松比为0.3,密度为1 440 kg/m3;弹丸密度为7 800 kg/m3。

图3 长丝束及平纹织物与弹丸的有限元模型Fig.3 Finite element model for yarn, plain weave and projectile.(a)Yarn model; (b) Model of projectile colliding a plain weave
4 结果与讨论
4.1 弹丸侵彻实验结果分析
图4示出单层平纹和双层平纹靶体在弹丸贯穿前后的入射速度-出射速度散点分布。通过有限元建模得出的理论数据,连接右上角和左下角的虚线表示当没有靶体时弹丸入射速度和出射速度之间呈线性关系。弹道极限是指弹丸能够贯穿给定类型和厚度及倾角的装甲目标所需的最低着速,它是衡量弹丸击穿靶板能力的重要指标。由图4可知:弹丸贯穿靶体前后的入射速度和出射速度呈非线性正相关,即在靠近弹道极限的速度范围内,出射速度随入射速度的增长较快;在远离弹道极限的速度范围内,出射速度随入射速度的增长逐渐放缓,曲线逐渐与虚线保持平行。这是因为在靠近弹道极限的速度范围内,弹丸的动能主要转化为靶体的动能和应变能;在远离弹道极限的速度范围内,靶体表现出非弹性的动态响应,材料更易损毁,吸收的能量降低[18]。将实验数据与有限元数据进行对比发现,实验与有限元模拟曲线增长趋势呈现出较好的一致性,但实验数据的出射速度较建模数据的出射速度低,意味着模型低估了实体试样的防弹性能。

图4 单层结构和双层结构实验及有限元建模入射速度-出射速度曲线Fig.4 Impact-residual velocity curves of experimental and finite element models for single and doule layer structures
图5示出层间间距变化对靶体吸能效果的影响。其中:Y轴为靶体吸收弹丸的动能(通过弹丸动能损失获得);X轴为双层芳纶平纹织物间相隔的距离。通过实验和建模获得的数据可知,靶体所吸收的能量随间距变宽先下降后上升。当间距到达一个临界值后,能量吸收将停止增长。使用单因素方差分析法分析所有靶体能量吸收的差异性,算得F值为6.059。当α=0.01时,F分布临界值F(8,18)=3.71;当α=0.005时,F分布临界值F(8,18)=4.28。二者均小于6.059,P<0.01,说明不同靶体之间差异性显著。如果将间距为0、2、3、4和6 mm的试样单独进行方差分析,则F值为0.234。当α=0.01时,F分布临界值F(4,10)=5.99;当α=0.005时,F分布临界值F(4,10)=7.34。二者均大于0.234,P<0.01,靶体间无显著差异。将间距为8、9、10和12 mm的试样单独进行方差分析,则F值为0.05,小于临界值F(3,8),P>0.01,靶体间无显著差异。也就是说,当层间间距控制在6~8 mm之间时,靶体的吸能性能有显著的提高;而层间间距小于6 mm或者大于8 mm时,靶体的吸能性能无显著差异。实验数据与建模数据之间的差异性主要体现在2个方面。

图5 靶体能量吸收随层间间距变化规律Fig.5 Energy absorption as a function of layer spacing for sample targets
1)由图5可知,建模数据表现得相对集中,而实验数据与建模数据相比更为离散。这主要是因为,在实验过程中弹丸与靶体接触时,弹着点的位置是不可控的。在有限元模型中,由于忽略了弹丸在行驶过程中受到的其他外界因素以及靶板安放位置的变化等不可控因素的影响,弹着点的位置始终在经纬纱交织点的正中央或者位于2根相邻长丝束之间,不发生变化,因此模型数据没有离散。当弹着点位于经纬纱交织点的正中央时,经纬纱受到弹丸拉伸作用发生断裂,靶体的贯穿主要是通过芳纶纤维的损毁造成的,靶体的能量吸收效果较好(见图6(a));当弹着点位于2根相邻的长丝束之间时,长丝束容易发生滑移,靶体的贯穿主要是通过芳纶纤维的横向偏移造成的,靶体的能量吸收效果较差(见图6(b))。

图6 被弹丸贯穿后的芳纶平纹织物Fig.6 Post-impacted aramid plain weaves. (a) Sample with filament damage; (b) Sample with filament lateral displacement
2)通过实验获得的弹丸动能损失数值比通过有限元建模得的弹丸动能损失数值大,也就是说有限元模型略微低估了靶体的实际吸能效果。使用单因素方差分析法分析二者之间的差异性,计算得到假设统计量F值为23.67,大于临界值F(1,22),P<0.01,说明实验数据与模拟数据具有明显差异。主要原因包括:有限元长丝束模型剪切模量和径向拉伸模量的设定值远高于实际长丝束的值;有限元长丝束模型由实体单元构成,在受力过程中不易发生形变。实体长丝束由单根长丝构成,受力状态下长丝与长丝之间接触碰撞并产生滑移,长丝束易发生形变。在以上2个原因共同作用下,有限元模型在弹着点处更加容易出现应力集中现象,导致单元过早损毁,降低模型的能量吸收。尽管模拟数据和实验数据存在差异性,但二者变化规律非常类似,因此可以利用有限元模型分析不同间距靶体的吸能机制。
为深入研究间距对双层平纹结构能量吸收过程的作用机制,利用有限元模型分析靶体在弹丸侵彻过程中的形变、应力分布和能量变化规律。选取层间间距为0、3、6和9 mm的靶体作为案例进行分析。
4.2 双层间隔织物的横向形变和应力云图
图7、8分别示出间距为0、3、6和9 mm的靶体迎弹面与背弹面断裂时刻的横向形变和应力云图。可知,迎弹面和背弹面呈现出完全不同的动态响应。在迎弹面织物模型上,横向形变的宽度和应力分布随层间间距的变宽而增大;在背弹面织物模型上,模型的横向形变与应力分布的范围大致相同,但间距为0 mm的靶体展示出更为宽广的应力分布范围,更多的能量杯背弹面吸收意味着分布在织物模型平面上应力具有更高的强度。
4.3 吸收能量变化规律
为进一步量化靶体迎弹面与背弹面的动态响应,通过有限元软件的后处理功能,记录靶体的能量吸收随时间变化的规律。图9示出靶体的总能量吸收随时间变化的规律。层间间距为0、3、6和9 mm的靶体弹丸实际作用时间分别为81、100、125和150 μs。其中:层间间距为3 mm的靶体吸收的能量最少,约为3.93 J;层间间距为9 mm的靶体吸收的能量最多,约为4.87 J;层间间距越窄,曲线的初始模量越大,也就意味着靶体对弹丸的响应就愈加迅速。

图7 靶体迎弹面织物断裂横向形变及其应力云图Fig.7 Transverse deflections(a)and contour plots of stress distribution(b)for back layer
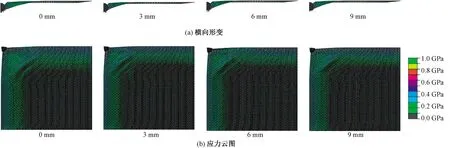
图8 靶体背弹面织物断裂横向形变及其应力云图Fig.8 Transverse deflections(a)and contour plots of stress distribution(b)for front layer
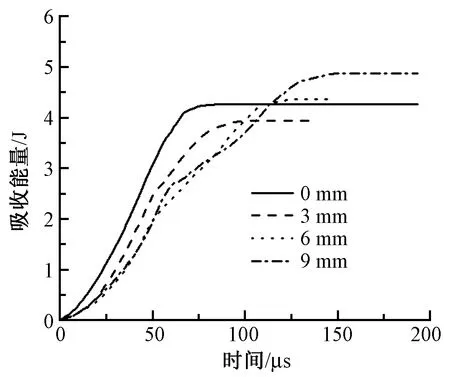
图9 靶体能量吸收随时间变化规律Fig.9 Energy absorption as a function of time
由于靶体吸收的能量主要转化为应变能和动能,利用有限元模型研究迎弹面织物和背弹面织物的应变能与动能的变化规律。图10、11分别示出迎弹面与背弹面织物应变能和动能随时间的变化趋势。可知,在弹丸侵彻过程中,所有靶体迎弹面织物的应变能变化曲线会出现一个峰值,此峰值所对应的时间点即为织物被弹丸完全贯穿的时刻,即织物的断裂时刻。断裂时刻略微受层间间距影响。层间间距越宽,贯穿时间点越延后,而迎弹层织物所积累的应变能就越多。研究表明,层间间距为9 mm的靶体在断裂时刻迎弹面织物所吸收的应变能几乎是层间间距为0 mm靶体的2倍。靶体的层间间距对迎弹面织物动能吸收的影响也具有类似的规律。由于层间间距的存在,背弹面织物对弹丸作用的响应会随着间距的增大而出现延迟。除此以外,层间间距为0 mm的靶体在断裂时刻能够吸收的应变能和动能最多,分别为0.907和0.921 J。其他靶体吸收的应变能和动能总量与此靶体大致相同。

图10 靶体迎弹面织物应变能和动能随时间的变化Fig.10 Change of time with strain and kinetic energy for front layer. (a)Strain energy;(b)Kinetic energy
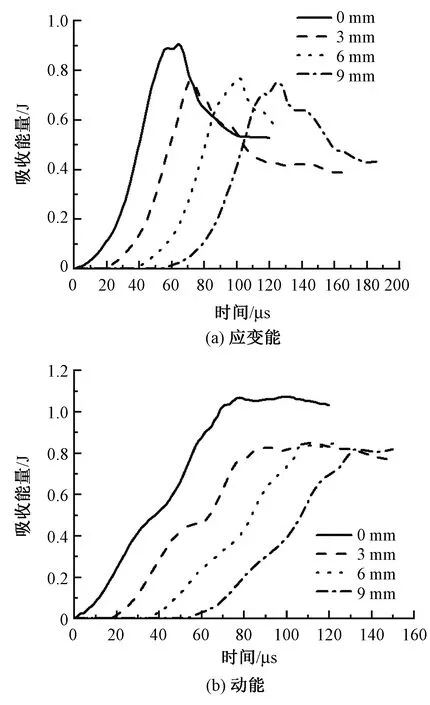
图11 靶体背弹面织物应变能和动能随时间的变化Fig.11 Change of time with strain and kinetic energy for back layer.(a)Strain energy;(b)Kinetic energy
4.4 层间间距与靶体吸能效果分析
层间间距与双层结构靶体抗侵彻性能之间并非呈简单的线性关系。随着层间间距的增加,靶体所吸收的能量呈现出先下降后上升的趋势,这与靶体迎弹面和背弹面织物的动态响应密切相关。
从图10可看出,不同靶体迎弹面的断裂时间随间距变宽而延后,也就是说迎弹面与弹丸接触的时间随层间间距的增加而变长。接触时间变长可以有效地增加迎弹面应变能和动能的吸收。关于层间间距对迎弹面断裂时间的影响,可做如下解释:靶体在弹丸侵彻的过程中,应力波不仅会在平面上沿着经纬纱方向传递,而且会沿着靶体的厚度方向传递。在厚度方向传递的应力波对材料造成挤压效果。在层间间距为0 mm的情况下,一部分应力波会从迎弹面传递给背弹面,另一部分应力波会沿着厚度方向反射回弹着点,如图12所示。在应力波反射的过程中,弹着点附近材料受到的挤压作用会得到增强,造成应力集中现象。应力集中不仅不利于能量的吸收,还会间接引发材料的拉伸作用[19-20];当材料受到的拉伸超过材料本身的拉伸强度时,材料发生断裂。当层间间距大于0 mm时,厚度方向传递的应力波会转换成材料的横向形变(见图8(b))。在此情况下,应力波不会回弹,弹着点附近材料因弹丸的挤压作用而产生的应力集中就会得到缓解,因此不容易发生断裂。
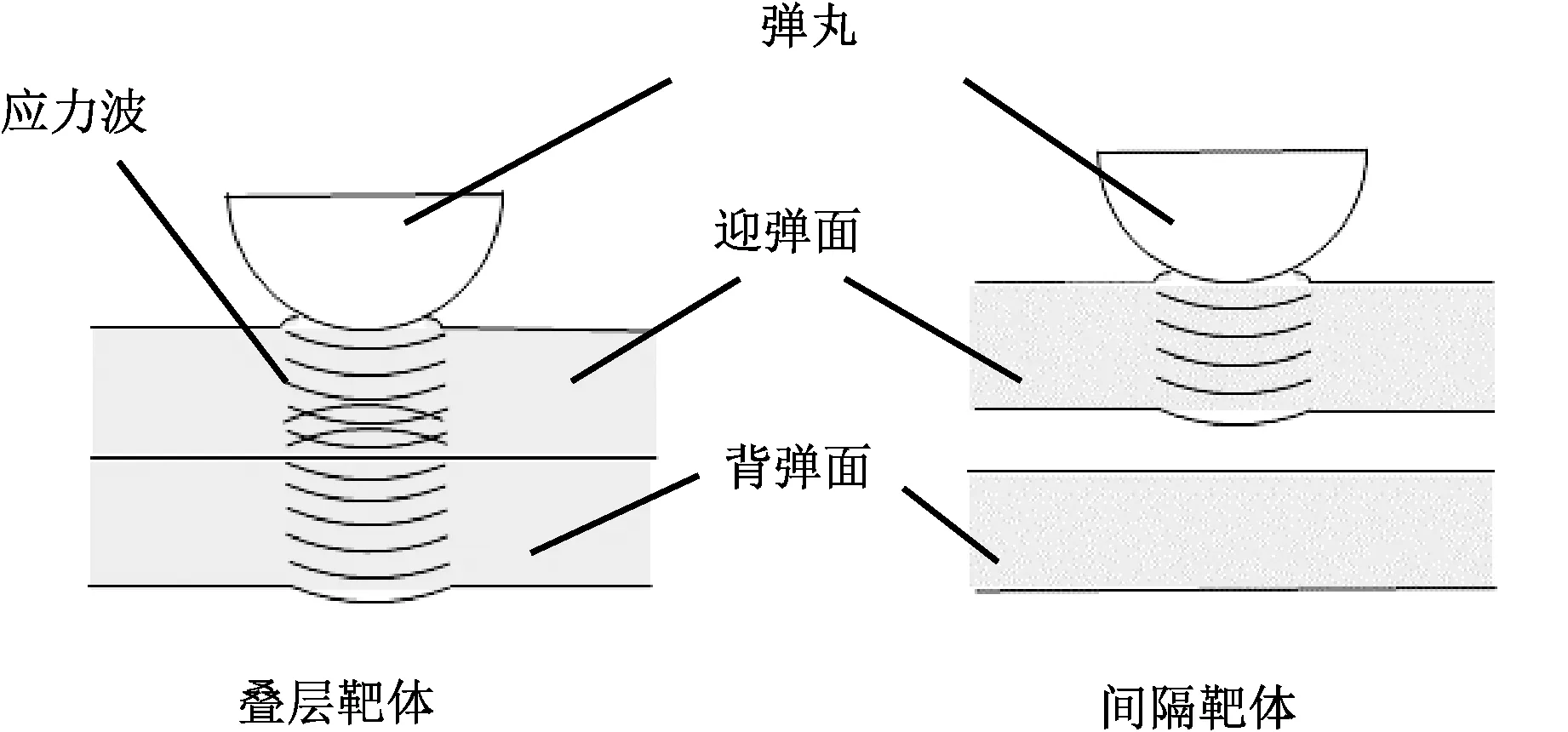
图12 弹丸冲击靶体示意图Fig.12 Schematic diagram of projectile colliding target
将图11中应变能随时间变化曲线往左侧平移,可以得出不同层间间距靶体背弹面与弹丸接触的时间。结果表明,虽然背弹面与弹丸接触的时间随层间间距的增加而延长,但是吸能总量的最大值却出现在间距为0 mm的靶体上。从图8可以看出,间距为0 mm的靶体在断裂时刻分布在模型平面应力的强度最高。这主要是因为此类靶体迎弹面与背弹面之间没有间隙,背弹面织物在弹丸接触靶体的初始阶段就受到较高程度的冲击载荷,因此在短时间内能够吸收较多的能量,但也容易过早断裂。如果迎弹面与背弹面之间存在间隙,在弹丸与靶体接触的初始阶段主要是迎弹面起到缓冲作用,背弹面不受影响。当弹丸接触到背弹面时,其动能已经损失了一部分,因此作用于背弹面的冲击载荷的程度相比于间距为0 mm的靶体较低,故层间间距较大靶体的背弹面材料吸能效果较差,但是与弹丸接触的时间相对来说也比较长。
Porwal等[16]通过力学分析模型发现:层间间距对多层结构靶体的V50起到负面作用;迎弹面和背弹面材料同时抵御弹丸侵彻的效果比单独抵御弹丸侵彻的效果要好。这个结论主要是通过分析模型获得的,而分析模型的缺陷之一在于无法把应力集中这一因素考虑进去,故迎弹面的能量吸收不会降低,而背弹面的能量吸收持续减少,导致靶体抗侵彻性能因层间间距的增加而降低。本文通过有限元建模发现,迎弹面吸收的能量随层间间距的增大而增加,背弹面吸收的能量随层间间距的增大而减少。在层间间距比较窄的情况下,如3 mm的靶体,由于迎弹面能量吸收的增加不能弥补背弹面能量吸收的减少,靶体的吸能总量略有下降;随着层间间距的不断变宽,迎弹面的能量吸收持续增加,而背弹面的能量吸收几乎保持不变,故靶体的吸能总量增加。
5 结 论
1)层间间距对靶体抗侵彻性能的影响较为复杂。靶体的吸能效果随间距变宽先下降后上升。当间距到达一个临界值后,吸收的能量将停止增长。间距越窄,靶体对弹丸的动态响应就越为迅速。
2)靶体迎弹面织物的断裂时刻随层间间距的变宽而略微延后,横向形变的宽度和应力分布的面积却随间距的变宽而增大,吸收的总能量也大幅度上升。这主要是因为层间间距过载会导致迎弹面弹着点附近材料发生应力集中现象。应力集中不仅会影响应力波的传递,而且会导致材料受到拉伸作用,引发材料过早断裂。
3)靶体背弹面织物的断裂时刻同样随层间间距的变宽而延后。与其他靶体相比,间距为0 mm的靶体呈现出更为高强度的应力分布。这主要是因为,背弹面织物在弹丸接触靶体的初始阶段就受到较高程度的冲击载荷,因此在短时间内能够吸收较多的能量,但也容易过早断裂;如果迎弹面与背弹面之间存在间隙,弹丸作用于背弹面冲击载荷的程度相对来说比较低,故背弹面吸能效果较差,但是与弹丸接触的时间相对来说也比较长。

