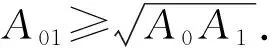Brunn-Minkowski面积不等式的两种证法
汪小玉, 何 梅
(1.合肥师范学院 数学与统计学院, 安徽 合肥 230601;2.淮阴师范学院 数学与统计学院, 江苏 淮安 223300)
0 引言
几何不等式一直是几何学中的一个研究热点,而Brunn-Minkowski 面积不等式是几何不等式中的典型不等式,在凸体理论中一直备受关注,与著名的等周不等式有密切联系[1-4],并且被推广到关于体积的不等式形式.本文借助高等数学中的傅里叶级数和函数的凹凸性,给出 Brunn-Minkowski面积不等式的初等证法.
1 预备知识
设γ为平面上C1类正定向闭凸曲线,O为γ所围区域内一点,在此选择O作为坐标原点.若p表示从O到γ上点(γ1,γ2)处的切线Γ的垂直距离,φ为x1轴的正半轴到p的垂直射线的夹角,则p为φ的单值函数,且p是一个以2π为周期的周期函数.切线Γ的方程可写成,
x1cosφ+x2sinφ=p(φ)
(1)
γ上所有点的切线构成一个单参数直线族,式(1)为其参数方程,φ为参数.曲线γ可以看作是此直线族的包络,因此曲线γ可以用参数φ表示为,
(2)
其中p′(φ)表示p(φ)关于φ的导数.(φ,p(φ))通常称为凸曲线γ的切线极坐标,p(φ)称为曲线γ的 Minkowski 支撑函数,在下文中简称支撑函数.
对式(2)两边关于φ求导,可得,
(3)
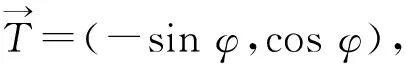
(4)
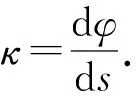
为了用支撑函数表示曲率κ,要求曲线γ至少是C2的. 式(3)关于φ求导后,带入κ的计算公式可得,
(5)
曲率半径
(6)
若L,A分别表示曲线γ的长度和γ所围区域D的面积,则由p(φ)的周期性可得,
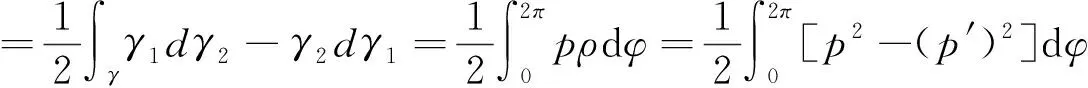
(7)
(8)
式(7)称为 Blaschke 公式,式(8)称为Cauchy公式.
设D0,D1为凸区域,其面积分别记为A0,A1,边界曲线周长分别记为L0,L1.定义凸区域D0,D1的Minkowsks和[1]为,
由式(4)可知,
由此可知D2也是凸区域,其支持函数p2=p0+p1.
引理1 设p0,p1分别为凸区域D0,D1的支撑函数,则D2=D0+D1的面积、周长分别为,
L2=L0+L1,A2=A0+2A01+A1.
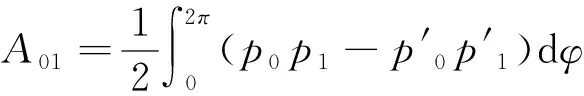
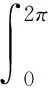
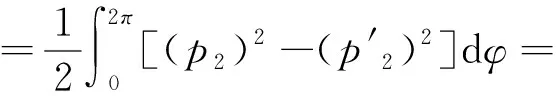
2 混合面积公式
由于D0+D1=D1+D0,所以混合面积A01=A10.下面利用微分和积分的运算关系,可得混合面积的一些不对称计算公式,为下文中傅里叶级数表示法的计算提供依据.
由全微分公式,
可得,
因此有,
由式(5)和式(6)可得,
类似可得,
(9)
3 几何量的傅里叶级数表示
凸区域D0,D1的支撑函数分别记为p0,p1,曲率半径分别记为ρ0,ρ1,其傅里叶级数表示法为[2-5],
带入式(7)、式(8)计算得,
(10)
Lj=2πaj0,
(11)
为了把上述各几何量表示成内积形式引入内积序列空间,其内积定义为,
利用上述内积定义,将式(10)、式(11)改写为,
(12)
(13)
4 主要结果
引理2设α0,α1,β0,β1为实数,则有,
(14)
或写成,
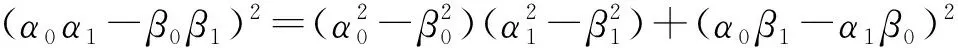
定理1(Brunn-Minkowski面积不等式)设凸区域D0,D1的面积分别为A0,A1,A01为混合面积,则
(15)
证明把式(12)、式(13)带入Cauchy-Schwarz不等式
〈(a,b),(c,d)〉2≤〈(a,b),(a,b)〉〈(c,d),(c,d)〉,
计算可得,
(16)
则有,
(17)
联立式(16)、式(17)可得,
由面积和周长的相关不等式可知,上式中左右两边底数均为正数,从而两边开方得,
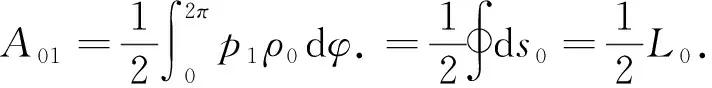
对于Minkowski和定义的推广形式[1,4]为:D(t)=(1-t)D0+tD1,0≤t≤1.D(t)的支持函数p(t)=(1-t)p0+tp1.类似引理1可得如下引理.
引理3对于凸区域D(t),其面积A(t)和边界曲线的周长L(t)有,
L(t)=(1-t)L0+tL1,A(t)=(1-t)2A0+2(1-t)tA01+t2A1
(18)
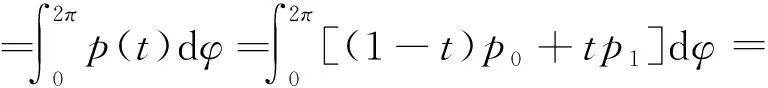
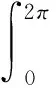
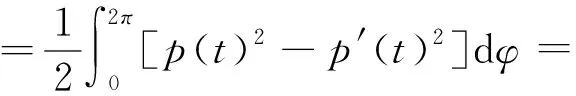
(1-t)2A0+2(1-t)tA01+t2A1.
引理4[3]混合面积满足下面不等式
(19)

证明由式(18)和式(19)可得,
A01=(1-t)2A0+2(1-t)tA01+t2A1≥
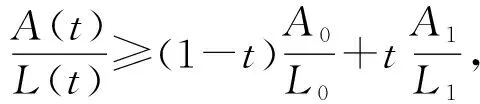
从而有,
上式移项得,
(20)
另一方面,
(21)