Lomax分布形状参数变点的贝叶斯估计

沙雪云， 周菊玲， 董翠玲

(新疆师范大学 数学科学学院， 新疆 乌鲁木齐 830017)

0 引言

变点问题是近几年统计学的热点研究问题，变点模型则是研究变点问题的一种非常重要的统计模型，其应用广泛，研究方法多样. 常用的研究方法有贝叶斯方法、极大似然法和最小二乘法等，其中贝叶斯方法在解决变点问题上综合了先验信息以及样本信息，使得判断更为准确. MCMC算法是一种高效的贝叶斯方法，将Gibbs抽样与M-H抽样相结合的算法，根据参数的满条件分布形式来选取Gibbs抽样和M-H抽样，进而得到参数的Gibbs样本，最终把Gibbs样本的均值作为各参数的贝叶斯估计. Lomax分布是一种非常重要的寿命分布，具有单调的失效率，所以在寿命试验的数据处理中起着至关重要的作用. 姚惠等人分别研究了基于没有任何数据缺失的情况下，Lomax分布在熵损失函数、Linex损失函数等不同的损失函数下参数的bayes估计[1-4]. 龙兵等人针对在数据不完整的情况下对Lomax分布进行各参数估计[5-8]. 岑泰林讨论了在完全数据和随机删失数据不同情况下Lomax分布的参数估计问题[9]. 但是，目前对Lomax分布单变点问题的研究较少. 本文将研究在尺度参数已知的情况下，对Lomax分布的形状参数及变点位置进行贝叶斯估计，并运用MCMC算法进行随机模拟，结果表明，各参数的估计值与真实值的MC误差较小，说明各参数估计值在较高水平上是行之有效的.

1 Lomax分布及变点模型

设随机变量X服从参数为λ,θ的Lomax分布，则分布函数和密度函数分别为

其中尺度参数λ>0，形状参数θ>0.

假设样本yi(i=1,2,…,n)值服从Lomax分布，若在序列{y1,y2,…,yn}存在变点，则在该序列中存在一个时间点，在该时间点的前后样本值yi所服从的Lomax分布的尺度参数θ也将会发生变化，即在这一时间点之前的序列服从参数θ1为的Lomax分布，在这一时间点之后的序列服从参数为θ2的Lomax分布，称该时间点为序列中的一个变点，当在序列中存在两个及以上的变点时，则称此模型为多变点模型. 含有k个未知变点的Lomax分布的模型为

(1)

其中m1,m2,…,mk是所要求得未知变点参数，θ1,θ2,…,θk分别为不含变点区间的尺度参数. 针对含有多个未知变点的情况，可以采用二分分段法和贝叶斯因子进行逐段寻找，其中用贝叶斯因子来判断序列是否存在单个变点可以借助于Kass和Raftery在1995年提出的贝叶斯因子模型选择的一般准则[10]. 下面给出用二分分段法及贝叶斯因子解决多变点问题的具体思路：

在处理多变点问题时，首先需要确定变点是否存在，若存在变点，则要在给定变点个数的情况下求出变点的所在位置，借助二分分段法及贝叶斯因子先来确定变点的个数，然后判断在一个序列集中是否存在一个变点及这个变点所在的位置.

第1步：在整个序列集S中，利用贝叶斯因子来检测是否存在单个变点. 若贝叶斯因子检测得不存在变点，就表示整个序列集不存在变点，则终止程序；否则就能够检测出这个序列里的第一个变点；

第2步：基于检测出的第一个变点，将整个序列集S分为两个子序列，对每个子序列，用第1步分别寻找出一个变点，一直持续这个过程直到在每个子序列中找不到变点为止.

利用二分分段法，只需要检测并估计出单个变点的位置，接下来，利用贝叶斯方法来讨论Lomax分布的单变点问题.

假设变点个数有且只有一个，Lomax分布形状参数单变点模型为

(2)

其中x>0,θ1>0,θ2>0,λ=c(c为常数)，且m,θ1,θ2均为未知. 当θ1≠θ2时，m=2,3,…,n-1就是所要研究的变点，同时还需要对变点m以及参数θ1,θ2进行贝叶斯估计.

2 单变点模型参数的贝叶斯估计

当θ1≠θ2时，设m为变点，记α=(m,θ1,θ2)，则此变点问题的似然函数为

1)θ1,θ2通过用Fisher信息阵确定无信息先验分布.

首先, 写出样本似然函数为

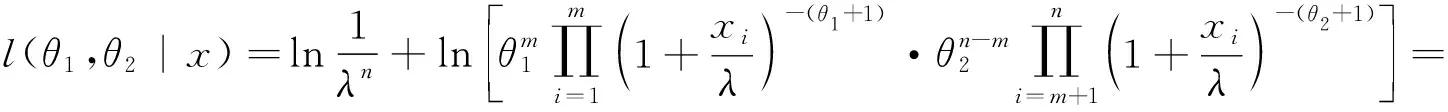
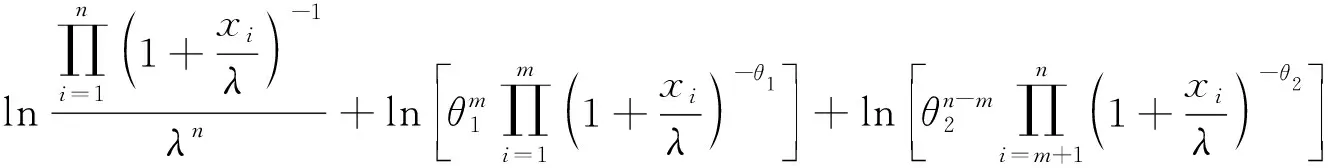
通过样本似然函数可得到与其相关的样本的信息矩阵,

进而得到θ1,θ2的无信息先验矩阵为,

最后θ1,θ2的无信息先验分布为

由贝叶斯公式求得联合后验分布为,

π(α|x)∝L(α|x)π(α)=

各参数满条件分布为,

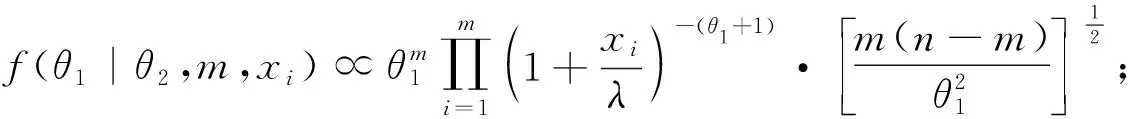
2) 取θ1,θ2的共轭先验分布为Ga(bi,ci)，即

且m,θ1,θ2相互独立，由贝叶斯公式得联合后验分布为,

π(α|x)∝L((α|x)π(m)π(θ1)π(θ2))∝

可得各参数满条件分布为,

3 随机模拟

下面进行随机模拟估计，通过上述分别得到了在无信息先验分布和共轭先验分布下的Lomax分布变点位置及各参数的满条件分布，可以利用MCMC算法对变点位置及各参数进行随机模拟估计，由于参数θ1,θ2,m的满条件分布都较为复杂，用Gibbs方法对样本进行抽样较为困难，所以利用M-H方法对各参数θ1,θ2,m满条件分布进行抽样.

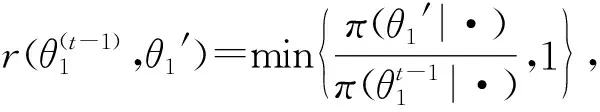
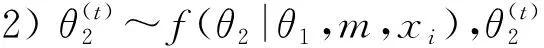
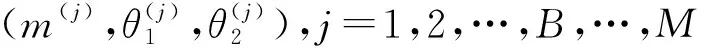
取随机产生n=183个数据作为样本，参数(m,θ1,θ2,λ)的真实值取(100,3,18,5)，即，

(3)

利用得到的各参数满条件分布，运用MATLAB软件来进行MCMC模拟，在模拟过程中检验模型参数的收敛性，通过输入多组初始值，形成多层Markov链，再用MATLAB软件对参数进行多层Markov链迭代分析，当参数m,θ1,θ2收敛时，Markov链迭代图将趋于重合. 为确保参数的收敛性，先进行10 000次的预迭代的基础上在进行20 000次迭代，即从第10 001次开始至30 000次开始迭代，可得MATLAB的运行结果，如表1所示.

当θ1,θ2的先验分布为无信息先验分布时:

表1 无信息先验分布下，参数m,θ1,θ2的贝叶斯估计

当θ1,θ2取共轭先验分布时，θ1～Ga(15,3.2)，θ2～Ga(27,1.2)，

表2 共轭先验分布下，参数m,θ1,θ2的贝叶斯估计

对模拟结果进行分析，首先，通过表1、表2可以观察到对参数选取不同的先验分布后，分别对它们进行随机模拟，得到的估计值与真实值的MC误差均不超过2%，说明各参数的估计值在较高水平上是有效的；其次，可取[2.5%分位数，97.5%分位数]作为参数置信水平为0.95的置信区间，从表1、表2可以看出置信区间较窄，区间估计效果良好；最后，通过图2、图4可以看出变点m的两条Markov链图像趋于重合，收敛性较好. 综上分析，利用MCMC算法得到的参数估计及变点位置估计的效果都较为理想，因此使用该方法处理Lomax分布的变点问题是可行且有效的.