河南地区动力煤发热量计算数学模型的建立及评价

刘松洋 石素娟 李国超

（平顶山姚孟发电有限责任公司，河南 平顶山 467000）

0 引言

煤的发热量对于燃煤发电企业是一项重要的技术及经济指标，不仅是商品煤计价的主要依据，也是影响锅炉安全高效运行的重要参数。 众所周知，煤炭采购占燃煤发电企业发电总成本的70%左右。 因此，燃煤发电企业和煤炭生产供应商均高度重视煤的发热量检测结果，煤的发热量也是燃煤发电企业和煤炭供应商在燃料管理过程中重点监督的内容。

目前， 煤的发热量主要依靠氧弹热量计直接测定或模拟计算。 氧弹热量计的测定方法是选用已知热容量的氧弹热量计， 称取一定质量煤样在充有过量氧气的氧弹内充分燃烧，根据量热系统的温升，进行热校正后最终得到发热量测定结果， 这种测定法在燃煤发电企业已经推广普及。模拟计算是通过煤的全水分、工业分析、 全硫及元素分析等数据进行建模并计算煤的发热量， 该方法在某些无法进行发热量实测的企业得到较多的应用[1]，同时也应用于对氧弹热量计检测结果的比对校核。氧弹热量计测定结果的准确性受环境温度、内外桶水温、充氧压力及操作规范等诸多因素的影响，在日常管理中需对其结果进行监督校核。 通过建模模拟计算煤的发热量， 可以方便地计算燃煤发热量并对燃煤发热量测定结果的准确性进行监督校核。

本文选用河南地区150 个不同矿点或批次的动力用煤，检测其全水分、水分、灰分、挥发分、全硫及发热量，对检测结果进行回归分析，建立了适用于河南地区动力煤发热量的数学模型，利用数学模型的计算值与氧弹热量计的实测值进行比较分析，验证该数学模型的准确性和实用性。

1 模型的建立

本文统计了河南地区150 个不同矿点或批次的煤样，所选取煤样尽可能覆盖河南地区各个矿点。 将所选取煤样分别进行采样、制样及化验。 化验项目包括全水分、水分、灰分、挥发分、全硫及发热量。

将化验数据进行统计分析，考虑到数学模型对于煤炭企业的实用性，尽可能将数学模型进行简化。 模型采用多元线性回归方法，以影响燃煤收到基低位发热量计算结果的参数 （全水分Mt、 空气干燥基水分Mad、干燥基灰分Ad、干燥无灰基挥发分Vdaf、干燥基全硫 St，d）为自变量，以收到基低位发热量 Qnet，ar（J/g）（以下简称发热量）为因变量，得到线性回归方程。

令：y=Qnet，at，x1=Mt，x2=Mad，x3=Ad，x4=Vdaf，x5=st，d。

建立线性回归方程：

y=a+bx1+cx2+dx3+ex4+fx5

将采集的150 个煤样的化验结果进行计算，求解结果如下：

Qnet，ar=32 731-300Mt-165Mad-330Ad+5.7Vdaf+251St，d

此方程相关性系数R2=0.997，接近于1，且F=9 080，说明具有较强的显著性。

2 模型的检验

数学模型建立完成后，需进行模型检验。 选取河南地区某一燃煤电厂为研究对象， 随机抽取10 个批次的入厂煤，按照相关标准进行全水分Mt（%）、空气干燥基水分 Mad（%）、干燥基灰分 Ad（%）、干燥无灰基挥发分 Vdaf（%）、干燥基全硫 St，d、收到基低位发热量Qnet，ar（J/g）的测定。 将发热量 Qnet，ar的实测值与模型计算值进行对比，结果如表1 所示。

从表1 可知，发热量实测值与数学模型计算值的差值绝对值最小为-22 J/g， 最大值为239 J/g。 根据GB/T 213—2008[2]规定，煤的发热量测定再现性临界差为300 J/g，数学模型的计算值与实测值的差距均小于此再现性临界差。 因此，可初步判断数学模型具有比较高的准确性。

参照GB/T 19494.3—2004[3]，对发热量实测值与数学模型计算值进行统计分析，发热量的差值平均值d=90，标准差sd=120.5020，并进行数理统计。 将煤的发热量测定标准GB/T 213—2008 给出的再现性临界差300 J/g 为最大允许偏倚值，即B=300，进行t 检验，结果如下

由 GB/T 19494.3 表 12， 查得自由度 n-1=9 情况下单尾 tβ=1.833，即 tnz＞tβ，证明差值平均值显著小于发热量的再现性临界差， 可接受为不存在实质性偏倚。说明该发热量计算数学模型具有一定的正确性和实用性，可以较为准确地计算河南地区煤的发热量。

与0 有显著性差异检验结果如下：

由 GB/T 19494.3 表 12， 查得自由度 n-1=9 情况下双尾 tα=2.262，即 tz＞tα，证明不能接受为无偏倚，即存在小于300 的偏倚。这也说明数学建模与实测值比起来还是存在一定的差距， 尽管这样的差距并不大，但是并不能被忽略。这可能是本文数学模型所选取样本数为150，无法做到完全覆盖河南地区所有煤种情况。 河南地区煤炭种类相对丰富，单一的数学模型难以做到对所有煤种都具有较高的适应性，所以数学模型的计算值与实测值始终存在一定的差距。

对于燃料管理工作者而言，在开展发热量日常化验的同时，利用数学模型对化验结果进行检验，以此快速判断发热量化验结果的准确性。燃煤发电企业及煤炭生产企业普遍采用发热量实测值作为结算计价依据，数学模型的建立对煤质监督具有一定的借鉴意义， 可作为河南地区煤炭质量检验的辅助监督方法，从而在企业煤炭管理工作中发挥作用。

3 结论

研究选取150 个河南地区动力煤，通过煤的全水分、水分、灰分、挥发分、全硫及发热量的化验结果，建立河南地区动力煤的发热量计算数学模型。通过实际应用验证，证明该数学模型具有较高的准确性，可推荐作为河南地区燃煤电厂及煤炭生产企业煤炭质量检验的辅助监督方法，有利于企业煤炭管理工作水平的提高。

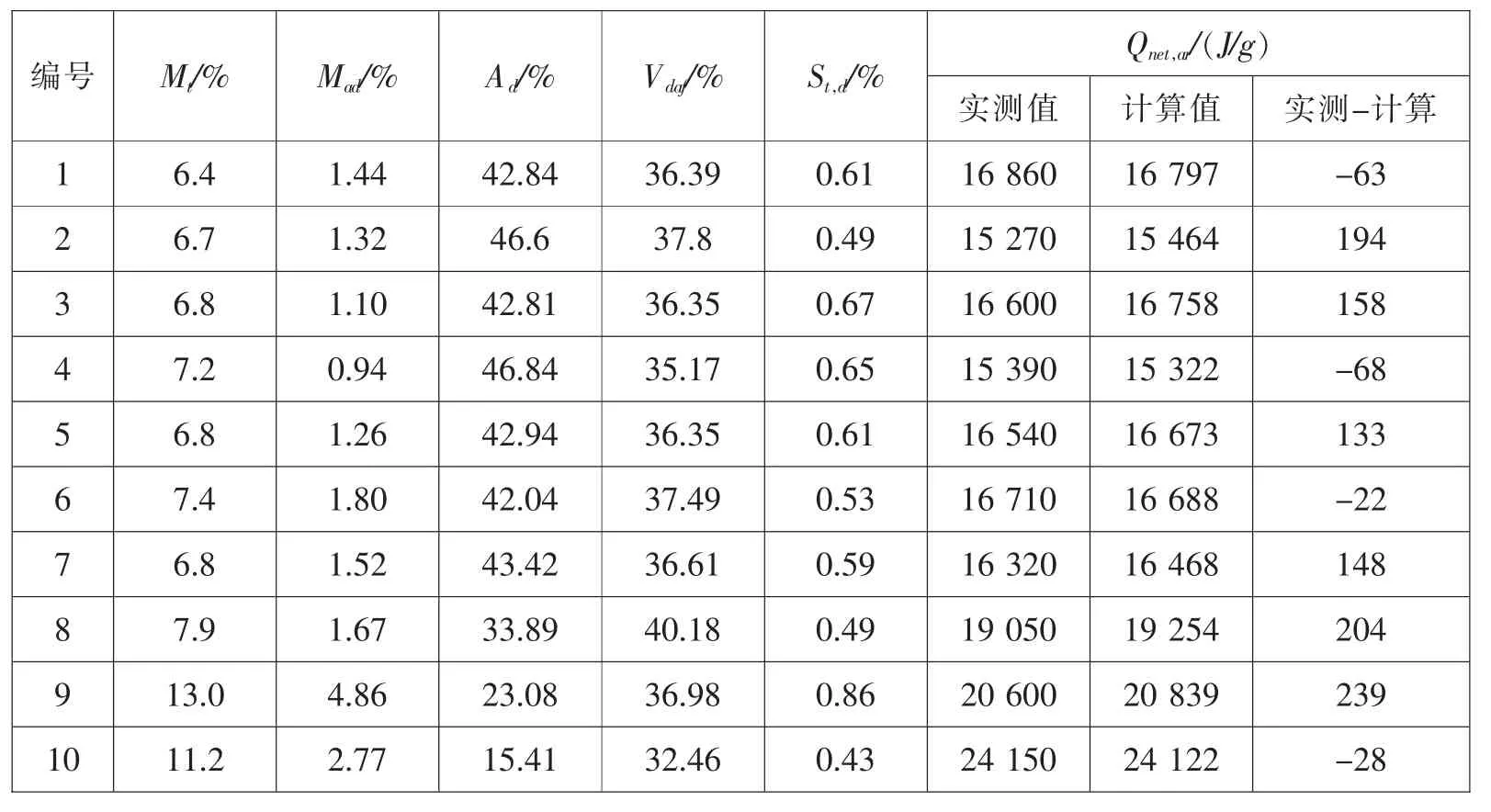
表1 发热量实测值与计算值比对